Сохранение остаточных напряжений на границе фазового перехода в реологической среде

Реологическое поведение мерзлых грунтов описывается моделями теории наследственной ползучести с различными временными ядрами [1, 2]. В теории консолидации водонасыщенных грунтов для учета реологических свойств скелета также применяются модели линейной наследственной ползучести [3, 4]. Данные модели описывают реологическое поведение различных сред при непрерывной истории деформирования. В случае же, когда в ходе деформирования в среде происходят фазовые переходы, и деформации на фронте фазового перехода терпят разрыв, необходимо учитывать влияние предыстории нагружения среды до фазового перехода. Для однородных сред с наследственной ползучестью, претерпевающих фазовый переход, была предложена гипотеза о сохранении остаточных напряжений при фазовом переходе, позволяющая учитывать влияние истории деформирования среды до фазового перехода [5]. Для задачи фильтрационной консолидации грунтов необходимо обобщить эту гипотезу на случай пористой среды с поровым заполнителем, претерпевающий фазовый переход первого рода.

Поведение водонасыщенной упругопористой среды в [6] описывается системой следующих линеаризованных уравнений: - уравнения неразрывности жидкой фазы

- уравнений движения вязкой жидкости

k 8 p ц 8x ₍

^{+ m} 0

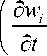
^ ui- 1= 0 d t J

- и уравнений равновесия твердой фазы

do,f

-^p 5ij = 0, dxi    dxi

d m      d p     ^{d e} 2 л

--+ в m — + mn —2 = 0, dt    2     dt     0 dt      ,

- уравнения неразрывности твердой фазы

d m в dO ~8t   3 "dT

, x dp          x^d e

- Д (1 - m o ) d p - (1 - m o )-1 = 0, о t             о t

где u i ,w i – компоненты перемещений соответственно твердой и жидкой фаз; m – пористость; e 1 ,e 2 – объемные деформации твердой и жидкой фаз; σ ij ^f – эффективные напряжения в пористой среде; p – поровое давление; σ ij – полные напряжения, действующие на насыщенную пористую среду; β 1 , β 2 – коэффициенты упругой сжимаемости твердой и жидкой фаз; μ – коэффициент вязкости жидкости; k – проницаемость среды.

Система уравнений (1) - (4) замыкается определяющими соотношениями, представляющими обобщение закона Гука для насыщенной упруго-пористой среды [7]:

o i, = ² G ^{(1 - m} 0⁾ E i_j ⁺ K ^{(1 - m} 0 ) в 1 5 у ⁺ ^ 0 p S y , (5)

где G (1 – m 0 ), K (1 – m 0 ) – модули сдвига и объемной упругости пористой среды (скелета); ε 0 = β 1 K (1 – m 0 ) – показатель сцементированности пористых горных пород. Заметим, что для мягких горных пород (сыпучие среды, грунты) ε 0 <<1, а для сильносцементированных горных пород (например, пористый базальт, бетон) ε 0 ≈1 [6]. Исключая из уравнений (1) - (2) производную пористости и используя соотношения (5), получим из (3) уравнение фильтрации, которое в одномерном случае будет иметь вид:

^{[ в} 1 ⁽ 1 ^- m 0 ) ^{+ в} 2 ^m 0 - P \ ^£ 0 ] | p ^{+ (1} - ^ 0 ) ^ ed =^"[ Ip ], d t dt dx ( ц dx J

Если воспользоваться предположением о пропорциональности объемной деформации скелета и порового давления, можно из (6) получить основное уравнение фильтрационной консолидации [3]:

дp _ д2 p дt     v дx2 ’                    (7)

где c v - коэффициент консолидации.

Для одномерного случая из (4) получим уравнение:

[ K - 2 G ] ( 1 - m ₀      - ( 1 - _{£ o} ) d p - 0,

V 3   )        д x          д x

На внешней границе талой области x =0 должны учитываться следующие граничные условия:

• -   нагружения P ₀( t )= o xx ;

• -    дренажа, если оттаивание идет в условиях отсутствия дренирования, то задается усло-

• вие непроницаемости ∂p/∂x=0, а если свободного дренирования, то p=0;

• -    условие теплообмена в виде граничных условий 1-го или 3-го рода для уравнения теплопроводности.

Кроме того на подвижной границе x=£ ( t ), где происходит фазовый переход, задаётся условие из закона сохранения массы [8]:

m о | 1 - ^Д|       - V ] - ,

V   Р2 ) dt где р 1, р2 -плотность льда и воды; v+,v- - значения скорости талого и мерзлого грунта на фронте фазового перехода.

В случае, когда пористая среда обладает ползучестью, вместо модулей сдвига и объемной упругости для скелета будут фигурировать соответствующие интегральные операторы и уравнение (5) можно представить в интегральном виде:

sf ( t ) - 2 G 0 ²⁾ (1 - m ₀) _Z af ( t ) - 3 K 0 ²⁾ (1 - m ₀)

(2)          (2)         (2)

j ⁽ t ) ^- J Rs ⁽ t ^{- TY}j  ^{( T} ) ^dT

e p⁾⁽ t ) ⁺ - 1 P ⁽ t )

- J RV ²⁾( t - T )

^{e (2)( T} ) ⁺ в"P ^{( t} )

dT

где s ij Y j ⁽²⁾ - девиаторы, а O f , e ^ - шаровые составляющие тензоров эффективных напряжений и деформаций скелета; R s ®( t ), R v ⁽²⁾ ( t ) - ядра интегральных уравнений релаксации [4]. В случае, когда ползучесть скелета описывается вязкоупругими моделями, ядра интегральных уравнений релаксации R s ⁽²⁾ ( t ) и R v ⁽²⁾ ( t ) представляют собой экспоненты с различными временами релаксации.

Рассмотрим соотношения, определяющие реологическое поведение сред при фазовом переходе льда в воду в порах [2]. Допустим, что реологическое поведение мерзлого грунта описывается линейным интегральным уравнением наследственной ползучести [1]. Уравнения релаксации для шаровых составляющих и девиаторов тензора напряжений будут иметь вид:

t

a ⁽¹⁾ ( t ) - 3 K^e ⁽¹⁾ ( t ) - J R^¹ ( t - т ) e ⁽¹⁾ ( т ) d T

t s<"(t) - 2G01)z™(t) - JRsh(t - т')r,'"(,T)dT

⁰                         (11)

где K0(1), G0(1) - модули мгновенной упругости, Rv(1), Rs(1) - ядра релаксации, соответственно для объемных и сдвиговых напряжений мерзлого грунта.

Обобщим гипотезу о сохранении остаточных напряжений в наследственно ползучих средах при фазовых переходах [5] на случай, когда мерзлый грунт рассматривается как однофазная среда, а талый грунт представляет двухфазную среду. Пусть в момент времени t= 9 в точке х = ^ ( 9 ) среда претерпевает фазовый переход (1→2). К этому моменту напряжения в среде в мерзлом состоянии (1) имеют значения:

а ⁽¹⁾ ( 6 ) - 3 K (1) e ⁽¹⁾ ( 6 ) - ^R ( ¹⁾ ( 9 - t ) e ⁽¹⁾ ( t ) dT

• (1)            (1)  (1)           (1)(1)

^sij ^{( 9 ) - 2 G} 0 ^Y ij ^{( 9 ) -} J ^Rs ^{( 9 - T ) Y} ij

Остаточные напряжения при этом задаются выражениями:

MX9 MX a2m(9) - - J Rv (9 - T)e 1 (t)dT остv s^v \(9) --f R^ (9 - т)/■ ,-()(t)dT ij (ост )v 7     0  5ij

В талом состоянии грунта полные напряжения задаются уравнениями:

ст ⁽²⁾ ( t ) = ³ K 0²⁾ (1 - m ₀) < -² ( t ) - (1 - s ₀) p ( t ) - j R V ²⁾ ( t - ^T )

^е?Ч^т ) + у P ^{( t} )

d T

s j ( t ) = 2 G 0²⁾ (1 - m 0 ) / *² ( t ) j R s ² ( t - т ) r _v ( t ) d т

Исключая мгновенно-упругие составляющие имеем для остаточных напряжений:

талом состоянии и к моменту времени t = 6 имела остаточные напряжения равные:

СТ ⁽²) ( t ) = - Jr ⁽²)( t - т ) ост        v

^{е (2)( т} ) + у" P ^{( т} ) ^dт

5(2)   (A = -XR(2)^(гМг sij (ост)(t)      Rs (t т )Yij    (т)

ст (2) ( 0 ) -- JR (2)( 0 - т ) ост        v 0	* (2)^ в *^ [ е1   ( т ) +Т р ( т Ч	dт
s )2)    ( 0 ) = -f R (2)( 0 - ij ( ост У '       s v	т lYij * (2) ( т ) dт

в талом грунте при оттаивании объемные деформации состоят из двух составляющих:

eg ( ост ^^Ч^ — ^Ы (14) где еУ_ост- - полная деформация талого грунта в момент фазового перехода t = у e i^A) (t₁)- объемная деформация из-за изменения плотности фаз.

Учитывая основное положение гипотезы, что при фазовом переходе сохраняются значения остаточных напряжений, определим значения деформаций для среды (2), допуская, что она с самого начала деформирования находилась в

Отсюда, приравнивая подынтегральные выражения для остаточных напряжений, получим соотношение:

* (2), ,   в1   *, , е1   (т) + у P (т) =

' ^-T' е«А) R<2)(6 - т)

* (2)      R( 1) (0 - т)

Yy   (0) =     --------

^J      r рф - т ) ^J

Таким образом, определяющие уравнения для талого грунта будем иметь в виде:

ст(2) (А-ЗК(2)      (e)2\tX-(X-£       f v — — о     (t) - 3K0   (1  m0)е1   (t)  (1  е0)p(t)   j                Rv   (t   т)е1   (т)UL

^{e )2)( т} )+у p ^{( т} ) ^dт

0 RV ²⁾( y - т )

^- j RV ²⁾( t ^- т )

⁰             r( ^( 0 - т )

• ^{(2)          (2)           (2)         (2)}           s ⁽¹⁾

sij  ⁽ t ) = ² G 0  ⁽¹   m0^)Yii  ⁽ t )   ^J Rs ⁽ t  ^т )               ^Yj ^(т ) ^ат

^{J                       J}       0            R ⁽²⁾( 0 - т ) ^J

• ^-    j ^{r(2 (} t ^{- тY}_zj ^{2) ( т} ) ^dт

⁰                                                                  (16)

Соотношения (11) - (16) учитывают наследственную ползучесть среды как до, так и после фазового перехода, причем вторые слагаемые в уравнении (16) учитывают эффект влияния на релаксацию напряжения в среде предыстории деформирования до фазового превращения порового флюида. В случае, когда пористая среда и мерзлый грунт вязкоупругие, то все ядра релаксации R v ⁽¹⁾ , R s ⁽¹⁾ , R v ⁽²⁾ , R s^(Т) являются экспоненциальными функциями от времени. Например, если поведение мерзлого грунта пористой среды (скелета талого грунта) при одноосном растяжении (сжатии) описывается линейной вязкоупругой моделью Максвелла, ядра релаксации имеют вид:

t

E (1)

^R 1 ^(,l( t )=^ ^{е т} 0

E (2)

^{R )2|(} t ) = У ^{е т} 0

г (1) ^т 0

t

Т²) ^т 0

где т о ⁽¹⁾ , т о ⁽²⁾ - время релаксации мерзлого грунта и пористой среды при одномерном нагружении.

Для простоты будем полагать, что коэффициенты Пуассона для пористой среды v ⁽²⁾ и мерзлого грунта v ⁽¹⁾ постоянные величины. Тогда упругие модули и ядра релаксации на сдвиг R s⁽^ ( t ), растяжение R 1 ⁽ i ) ( t ) и объемной деформации R v ^{( i )} ( t ) являются подобными:

R (1)    - R ( i ) (Лп(i ) 7 i ) (A ~ fii)i ) (An(i ) 7 i )   - 7 i ) (An(i )

Rv ( t ) ^— Rs ( t ) ⁿ 0 , Rs ( t ) ^— R i ( t ) n i , Rv ( t ) ^— R i ( t ) ⁿ 2 ,

3 K (i ) - 2 G₍

()  ( i )

ⁿ 0

( i ) ’ ^2G 0

( i )  ( i ) ( i ) ( i ) ( i )

- E 0 ⁿ 1  , 3 K 0   - E 0 n 2 ,

где „(i) - 1+v(i)   „(i)-___1___ n 0  = 1   9 (i) ’ n1   = 1 x (i)

1 - 2 v^{v 7}            1 + v^{v 7}

( i )

, n 2⁷ =

1 - 2 v ⁽ i )

- постоянные величины как в мерзлом ( i =1), так и в талом

( i =2) состоянии грунта. В этом случае уравнение релаксации для среды, претерпевающей фазовый переход 1 ^ 2 (15) и (16) можно записать в виде:

(2)       (2) (2)

a ^{v 7}( t ) = E^ гг^ •

,<2),

0 ^- m₀)« ( ⁾⁽ t ) ^- 0 ^- ^) P ⁽ t )

—

-

t - T

-

? E ("d.   t ( ²⁾

0 1» n ² '  ⁰

-

e

I T 0"

-

)

>^{( e - T} )

^T 0   J

^{е (1)( т} )d^T

-

-

t - T

1 7²⁾       Г⁽²⁾ Г (2)

f E 0_ „⁽²⁾_e ^T 0 ^e '

J r(2) n ² «

9 ^T 0               L

* _{( T} )   в

^{2 2}+-¹ P ^{( t} ) d^T 3

\

_S(2)_W - £(2)_и(2)_П _ _{m )7}(2)     ^E 0_ (1)

sij ⁽ t ) ^- E 0   n 1   ⁽¹    m0^)Yij ⁽ t )   ^J (1) n 1

^{0 T} 0

e

I

/D ^T 0

72) ^{(e - T} )

^T 0 J

Р’^т ) d^T

t - T

tE (²⁾   ₍₂₎    t (²⁾   ₍₂₎

J -⁰— n J ’e  ⁰  Л²\ ^T ) d^T

6t 0²⁾             j

При известных постоянных значениях ко- эффициентов Пуассона параметры вязкоупругих моделей определяются из экспериментов на релаксацию напряжений при одноосном нагруже- нии сухой пористой среды и мерзлого грунта.