Сокращенный метод калибровки фотокамеры с целью измерения расстояний

Попов Евгений Владимирович; Шеховцов Геннадий Анатольевич; Раскаткина Ольга Валерьевна; Popov E.V.; Shekhovtsov G.A.; Raskatkina O.V.

doi:10.14529/build190409

Научные статьи \ Прикладные науки. Медицина. Технология \ Инженерное дело. Техника в целом \ Строительство инженерных сооружений

Сокращенный метод калибровки фотокамеры с целью измерения расстояний

Автор: Попов Евгений Владимирович, Шеховцов Геннадий Анатольевич, Раскаткина Ольга Валерьевна

Журнал: Вестник Южно-Уральского государственного университета. Серия: Строительство и архитектура @vestnik-susu-building

Рубрика: Инженерная геометрия и компьютерная графика

Статья в выпуске: 4 т.19, 2019 года.

Бесплатный доступ

В статье описан сокращённый метод калибровки цифровой фотокамеры с целью использования её результатов для измерения расстояний путем обработки фотоизображений. В методе используется обработка фотографий горизонтального или вертикального базиса произвольной величины, расположенного лишь в начальной и конечной точках линии известной длины. Обработка фотоснимков заключается в измерении растровых координат в пикселях левого и правого или верхнего и нижнего концов базиса с помощью любого редактора растровых изображений. Установлено, что между произведением количества таких пикселей на соответствующие им расстояния и этими расстояниями существует прямая пропорциональная зависимость. На основании этого выведены формулы для вычисления с контролем измеряемого расстояния. Описан порядок выполненной калибровки фотокамеры и приведены результаты сравнения контрольных измерений с истинными их значениями. Установлено, что разработанный метод калибровки обеспечивает достаточную точность измерения расстояний путем обработки фотоизображений.

Еще

Калибровка, цифровая фотокамера, базис, пиксель, точность

Короткий адрес: https://sciup.org/147232159

IDR: 147232159 | УДК: 624-2/-9 | DOI: 10.14529/build190409

Abbreviated method of a camera calibration for the purpose of distance measurement

An abbreviated method of a digital camera calibration for the purpose of using the results for distance measurement by means of photo images processing is described in the article. The method is based on processing photo images of horizontal or vertical basis of an arbitrary size and located only at the start and end points of a line with the known length. Photo images processing involves measurement of raster coordinates in pixels of the left and right or upper and lower ends of the basis using any raster graphics editor. It is found that there is a direct proportional dependence between the quantity product of such pixels and the distances corresponding to them, and these distances themselves. For the reasons given, formulas for calculating, with respect to the measured distance control, are derived. The procedure for calibrating the camera is described, and the results of comparing control measurements with the true values are produced. It is found that the designed calibration method provides sufficient accuracy for distance measurement by means photo images processing.

Еще

Текст научной статьи Сокращенный метод калибровки фотокамеры с целью измерения расстояний

В ряде статей [1–5] отмечены достоинства цифровой фотограмметрии, позволяющие рекомендовать её для измерений геометрических параметров пространственных объектов бесконтактными методами. В работе [6] приведён метод использования цифровых фотокамер для определения расстояния до объекта съёмки. Метод основан на геометрической интерпретации зависимости измеряемых расстояний d_i от количества пикселей Δ _i , приходящихся на изображённый на снимках горизонтальный базис известной длины. Однако при этом для калибровки фотокамеры требуется выполнять большое количество снимков через определённый интервал расстояния, получая в результате их обработки криволинейную зависимость d i от Δ i , усложняющую процесс интерполяции при получении искомого расстояния. Калибровка фотокамеры является сложным и ответственным процессом, от результата которого зависит точность и достоверность определения геометрических параметров объекта. Изучению этого процесса посвящены исследования, описанные в работах [6–13].

В данной статье рассматривается сокращённый метод калибровки фотокамеры не только по горизонтальному, но и по вертикальному базису с целью упрощения последующей обработки результатов съёмки. Для этого предлагается вместо обобщённого коэффициента А , вычисляемого по приведенной в работе [14] формуле:

находить произведения (частные коэффициенты А i ):

А п i = d i х П i , А л i = d i х Л i ,

А н i = d i х Н i , А в i = d i х В i , (2) где П _i , Л _i и Н _i , В _i – растровые координаты курсора в пикселях, соответствующие положению на снимке правого и левого концов горизонтального базиса или нижнего и верхнего концов вертикального базиса.

Для иллюстрации разработанного метода рассмотрим результаты калибровки фотокамеры Nikon COOLPIX S9100. В качестве базисов были использованы две нивелирные 1,5-метровые рейки, скреплённые между собой в центральной их части в виде «креста» (рис. 1).

Фотокамера занимала положение в начале линии на расстоянии 3 м от её начальной точки и на высоте, равной половине рейки. Фотокамера была ориентирована на конечную точку линии так, чтобы «крест» занимал на снимке центральное положение.

В процессе моделирования было выполнено при неподвижном положении фотокамеры фотографирование «креста» через 1 м в интервале 3– 30 м горизонтальной линии. Каждую фотографию

а)

б)

Рис. 1. Схема измерения снимков по горизонтальному (а) и вертикальному (б) базису

(размером 4896×3672 пкс) выводили на экран монитора, открывали каждый файл с помощью программы Paint и, подводя курсор к левому и правому концам горизонтальной рейки, отсчитывали количество пикселей П и Л, Н и В, соответствующих каждому положению курсора (см. рис. 1). Результаты измерений снимков и их обработки для горизонтального базиса представлены в табл. 1 (графы 2, 3).

По значениям отсчётов П и Л можно определить средние отсчёты С = (П + Л)/2 (графа 4

табл. 1) и вычислить их отклонения от середины снимка р = С – 2448 (графа 5 табл. 1). Введя соответствующие поправки в отсчёты П и Л, получаем исправленные отсчёты Пи = П – р и Ли = Л – р (графа 6 и 7), приведённые к единой системе отсчётов относительно середины снимка.

Если по данным табл. 1 построить графики зависимости расстояния d от количества пикселей П и Л или Пи и Ли, то получим криволинейную зависимость (рис. 2), аналогичную работе [14], с возможностью использования формулы (1).

Таблица 1

Результаты калибровки фотокамеры Nikon COOLPIX S9100 и контрольные замеры по горизонтальному базису

d , м	Отсчёты по курсору, пкс			Поправка и исправленные отсчёты, пкс			Коэффициенты, м х пкс		d _выч, м	d в– d , м
d , м	П	Л	С	р	Пи	Ли	А Пи	А Ли	d _выч, м	d в– d , м
1	2	3	4	5	6	7	8	9	10	11
3	3354	1402	2378	–70	3424	1472	10272	4416	3,00	0,00
4	3133	1674	2404	–45	3178	1719	12710	6874	4,01	0,01
5	2989	1828	2409	–40	3029	1868	15143	9338	5,03	0,03
6	2892	1927	2410	–39	2931	1966	17583	11793	6,05	0,05
7	2822	1995	2409	–40	2862	2035	20031	14242	7,05	0,05
8	2780	2057	2419	–30	2810	2087	22476	16692	8,06	0,06
9	2737	2096	2417	–32	2769	2128	24917	19148	9,08	0,08
10	2704	2126	2415	–33	2737	2159	27370	21590	10,06	0,06
11	2684	2160	2422	–26	2710	2186	29810	24046	11,09	0,09
12	2667	2187	2427	–21	2688	2208	32256	26496	12,09	0,09
13	2650	2206	2428	–20	2670	2226	34710	28938	13,06	0,06
14	2633	2221	2427	–21	2654	2242	37156	31388	14,06	0,06
15	2622	2239	2431	–18	2640	2257	39593	33848	15,11	0,11
16	2608	2248	2428	–20	2628	2268	42048	36288	16,06	0,06
17	2598	2260	2429	–19	2617	2279	44489	38743	17,08	0,08
18	2591	2271	2431	–17	2608	2288	46944	41184	18,03	0,03
19	2582	2278	2430	–18	2600	2296	49400	43624	18,96	–0,04
20	2576	2288	2432	–16	2592	2304	51840	46080	19,99	–0,01
21	2571	2298	2435	–14	2585	2312	54275	48542	21,07	0,07
22	2564	2303	2434	–15	2579	2318	56727	50985	22,02	0,02
23	2562	2312	2437	–11	2573	2323	59179	53429	22,96	–0,04
24	2554	2314	2434	–14	2568	2328	61632	55872	23,90	–0,10

Окончание табл. 1

1	2	3	4	5	6	7	8	9	10	11
24	2554	2314	2434	–14	2568	2328	61632	55872	23,90	–0,10
25	2550	2320	2435	–13	2563	2333	64075	58325	24,91	–0,09
26	2547	2326	2437	–12	2559	2338	66521	60775	25,90	–0,10
27	2543	2331	2437	–11	2554	2342	68958	63234	26,97	–0,03
28	2540	2336	2438	–10	2550	2346	71400	65688	28,00	0,00
29	2536	2340	2438	–10	2546	2350	73834	68150	29,11	0,11
30	2528	2338	2433	–15	2543	2353	76290	70590	30,00	0,00
Контрольные замеры
5,47	2956	1896	2426	–22	2978	1918	14890	9590	5,51	0,04
9,21	2744	2114	2429	–19	2763	2133	24867	19197	9,24	0,03
15,54	2616	2244	2430	–18	2634	2262	39510	33930	15,55	0,01
22,19	2558	2299	2429	–20	2578	2319	56705	51007	22,18	–0,01
26,37	2535	2318	2427	–22	2557	2340	66469	60827	26,36	–0,01

По данным табл. 1 подсчитаем по формулам (2) коэффициенты А Пи , А Ли (графы 8 и 9). По их значениям построим графики зависимости А от расстояния d (рис. 3), представляющие собой прямые параллельные линии.

Как видно из рис. 3, зависимость А от d носит прямолинейный характер, поэтому на практике можно ограничиться определением А _Н и А _К всего по двум фотографиям базиса в начале и в конце контролируемого участка, а размер любого коэффициента А i может быть найден по формуле

( d i - d н ) ( A K - А н ) A i = A H + z , ,

⁽ d к ^- d н )

где А i , А Н и А К – размер коэффициента А соответственно на расстоянии d_i , d _н и d _к.

Прямолинейная зависимость А от d позволяет максимально упростить не только процесс калибровки фотокамеры, но и методику измерения и вычисления расстояний по горизонтальному базису. Действительно, если обозначим в формуле (3) А i = d i П i или А i = d i Л i , а также выразим

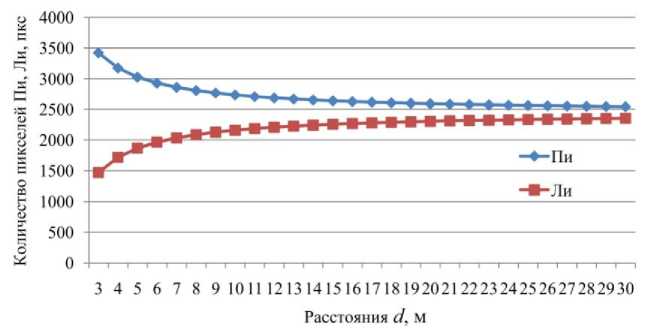
Рис. 2. Зависимость расстояния d от количества пикселей П и и Л и

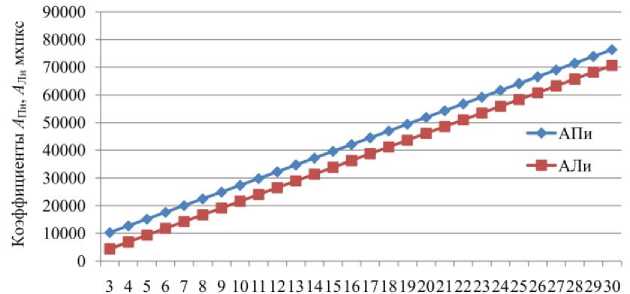
Расстояния d, м

Рис. 3. Зависимость коэффициентов А Пи и А Ли от расстояния d

k _п

A — A A - A кп нп кл нл d–d, л d–d, кн кн

то после соответствующих преобразований получим формулы:

. AПи. - dнkn AЛи. - dнkл di = i---------=-----i---------,

Пи i - k _п Ли i - k л

причём по обеим формулам будем получать одно и то же значение d .

Обратим также внимание на то, что полусумма ( k п + k л )/2 должна равняться по модулю постоянному числу (у нас 2448), участвующему в вычислении поправок р (графа 5 табл. 1). В нашем примере ( d _K – d _H) = 27 м, А _кп = 76290 пкс, А _нп = 10272 пкс, k _п = 2445,111 пкс/м, А _кл = 70590 пкс, А _нл = 4416 пкс, k _л = 2450,889 пкс/м, а полусумма ( k п + k л )/2 = 2448.

Для оценки точности разработанного метода были вычислены с помощью формул (5) при найденных коэффициентах (4) расстояния d выч (графа 10), и полученные результаты сравнены с соответствующими им табличными значениями d .

По разностям (dвыч – d) были найдены ошибки (графа 11), которые в диапазоне расстояний 3–30 м находилась в пределах от – 0,03 до +0,11 м, что в процентном отношении представлено на рис. 4, откуда следует, что относительная ошибка вычисления расстояний по формулам (5) не превышает 1 %, что является удовлетворительным.

Таким образом, для определения расстояния от фотокамеры до горизонтального базиса, расположенного в заданной точке съёмки, достаточно его сфотографировать, а затем в редакторе растровых изображений с помощью курсора измерить растровые координаты точек П и Л (см. рис. 1а). Результаты описанной обработки фотоснимков при контрольных замерах пяти произвольных расстояний представлены в табл. 1, при этом точность измерения находилась в пределах от –0,01 до +0,04 м.

Результаты измерений на базе фотоснимков для вертикального базиса (см. рис. 1б) представлены в табл. 2 (графы 2 и 3). Обработка снимков по изложенному выше методу заключалась в определении средних отсчётов С = (Н + В)/2 (графа 4), вычислении поправок р = С – 1836 (графа 5) и нахождении исправленных отсчётов Н и = Н – р и В и = В – р (графа 6 и 7).

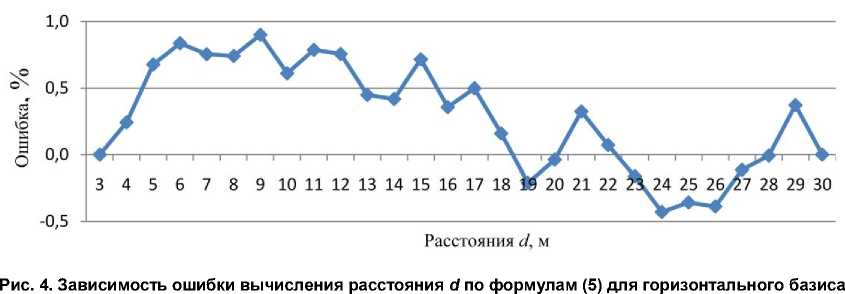
Таблица 2

Результаты калибровки фотокамеры Nikon COOLPIX S9100 и контрольные замеры по вертикальному базису

d , м	Отсчёты по курсору, пкс			Поправка и исправленные отсчёты, пкс			Коэффициенты, м х пкс		d _выч, м	d в – d , м
d , м	Н	В	С	р	Ни	Ви	^А Ни	А Ви	d _выч, м	d в – d , м
1	2	3	4	5	6	7	8	9	10	11
3	2840	872	1856	20	2820	852	8460	2556	3,00	0,00
4	2582	1115	1849	13	2570	1103	10278	4410	4,02	0,02
5	2433	1266	1850	14	2420	1253	12098	6263	5,05	0,05
6	2338	1362	1850	14	2324	1348	13944	8088	6,03	0,03
7	2260	1428	1844	8	2252	1420	15764	9940	7,07	0,07
8	2210	1483	1847	11	2200	1473	17596	11780	8,08	0,08
9	2164	1520	1842	6	2158	1514	19422	13626	9,12	0,12
10	2133	1553	1843	7	2126	1546	21260	15460	10,11	0,11
11	2108	1580	1844	8	2100	1572	23100	17292	11,10	0,10
12	2083	1599	1841	5	2078	1594	24936	19128	12,10	0,10
13	2065	1618	1842	6	2060	1613	26774	20963	13,09	0,09
14	2046	1631	1839	3	2044	1629	28609	22799	14,08	0,08
15	2031	1644	1838	2	2030	1643	30443	24638	15,09	0,09
16	2015	1652	1834	–3	2018	1655	32280	26472	16,07	0,07

Окончание табл. 2

1	2	3	4	5	6	7	8	9	10	11
17	2009	1668	1839	3	2007	1666	34111	28314	17,09	0,09
18	2000	1678	1839	3	1997	1675	35946	30150	18,09	0,09
19	1990	1685	1838	2	1989	1684	37782	31987	19,08	0,08
20	1981	1690	1836	–1	1982	1691	39630	33810	19,98	–0,02
21	1974	1698	1836	0	1974	1698	41454	35658	21,04	0,04
22	1967	1704	1836	–1	1968	1705	43285	37499	22,06	0,06
23	1960	1709	1835	–2	1962	1711	45115	39342	23,09	0,09
24	1956	1714	1835	–1	1957	1715	46968	41160	23,94	–0,06
25	1949	1717	1833	–3	1952	1720	48800	43000	24,94	–0,06
26	1941	1719	1830	–6	1947	1725	50622	44850	26,04	0,04
27	1938	1725	1832	–5	1943	1730	52448	46697	27,11	0,11
28	1935	1728	1832	–5	1940	1733	54306	48510	27,88	–0,12
29	1932	1734	1833	–3	1935	1737	56115	50373	29,11	0,11
30	1930	1738	1834	–2	1932	1740	57960	52200	30,00	0,00
Контрольные замеры
5,47	2362	1296	1829	–7	2369	1303	11845	6515	5,53	0,06
9,21	2145	1511	1828	–8	2153	1519	19377	13671	9,26	0,05
15,54	2016	1641	1829	–8	2024	1649	30353	24728	15,57	0,03
22,19	1960	1698	1829	–7	1967	1705	43274	37510	22,14	–0,05
26,37	1934	1715	1825	–12	1946	1727	50583	44889	26,39	0,02

Если по значениям исправленных отсчётов построить графики зависимости расстояний d от количества пикселей Н и и В и (рис. 5), то получим аналогичную рис. 2 их криволинейную зависимость с возможностью использования формулы (1).

Если по подсчитанным по формулам (2) коэффициентам АНи и АВи (графы 8 и 9) построить графики зависимости А от расстояния d (рис. 6), то аналогично рис. 3 получим прямые параллель- ные линии.

При использовании вертикального формулы (4) и (5) принимают вид:

A - A A - A кн нн кв нв н d–d, в d–d, кн кн

. A Ни - d н k н A Ви,. - d н k в

d, = i ----------= i ---------.

Ниi - kн Виi - kв базиса

По формулам (6), в которых ( d _K – d _H) = 27 м, А _кн = 57960 пкс, А _нн = 8460 пкс, А _кв = 52200 пкс,

А _нв = 2556 пкс, определяем k _н = 1833,333 пкс/м и k _в = 1838,667пкс/м с контролем ( k _н + k _в)/2 = 1836.

В графе 10 табл. 2 представлены расстояния d выч , вычисленные по формулам (7) с учётом коэффициентов (6). По разностям ( d выч – d ) найдены ошибки (графа 11), которые в диапазоне расстояний 3–30 м оказались в пределах от –0,12 до +0,12 м, что в процентном отношении иллюстрируется графиком на рис. 7. Из графика следует, что относительная ошибка вычисления расстояний по формулам (7) не превышает 1,3 %, что, как и в случае использования горизонтального базиса, является удовлетворительным.

Таким образом, аналогично использованию горизонтального базиса для определения расстояния от фотокамеры до вертикального базиса расположенного в заданной точке съёмки, достаточно на фотоснимке в любом редакторе растровых изображений измерить с помощью курсора растровые координаты в пикселах точек Н и В (см. рис. 1б).

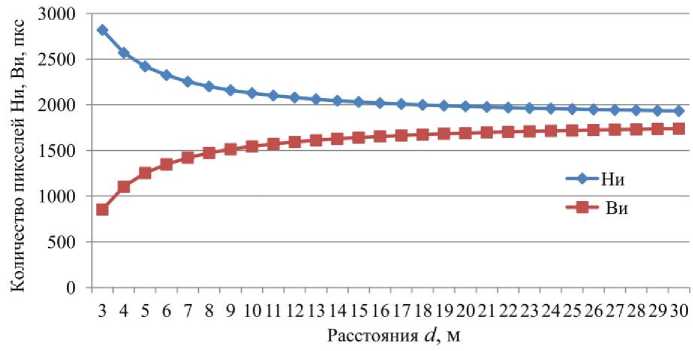
Рис. 5. Зависимость расстояния d от количества пикселей Н и и В и

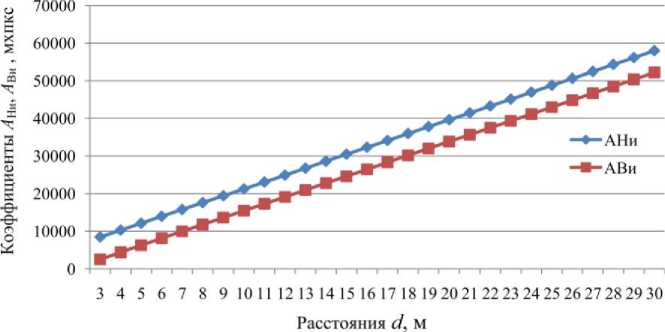
Рис. 6. Зависимость коэффициентов А Ни и А Ви от расстояния d

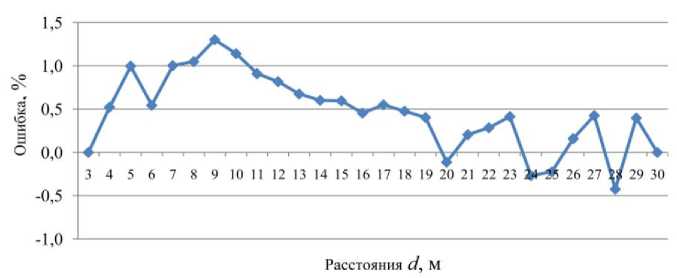
Рис. 7. Зависимость ошибки вычисления расстояния d по формулам (7) для вертикального базиса

Как показали контрольные замеры пяти произвольных расстояний (см. табл. 2), точность измерения не выходила за пределы диапазона от –0,05 до +0,06 м.

Следует отметить, что использование горизонтального или вертикального базиса позволяет производить контроль вычислительных операций по полусумме коэффициентов k п и k л или k н и k в и при этом получать два одинаковых значения искомого расстояния, что подтверждает точность предлагаемого метода.

Заключение

Выполненные контрольные измерения доказали применимость и эффективность разработанного сокращенного метода калибровки цифровой фотокамеры с целью определения расстояний путем обработки фотоснимков. В частности, метод может быть использован при определении деформаций инженерных сооружений. Разработанный бесконтактный метод измерения расстояний путем обработки фотоснимков не требует дорогостоящего оборудования и высокой квалификации исполнителей в силу своей простоты. Перспективным является использование функции приближения фотокамеры (Zoom) для повышения точности и дальности измерений.

Список литературы Сокращенный метод калибровки фотокамеры с целью измерения расстояний

Уставич, Г.А. О применении неметрических цифровых камер для инженерно-геодезических измерений / Г.А. Уставич, Я.Г. Пошивайло // Геодезия и картография. - 2005. - № 8. - С. 19-24.
Кацарский, И.С. О цифровой фотограмметрии и перспективах её применения / И.С. Кацарский // Геопрофи. - 2006. - № 6. - С. 4-8.
Барсуков, К.Г. Исследование возможностей неметрических цифровых фотоаппаратов при решении инженерно-строительных задач / К.Г. Барсуков // Научный вестник Воронежского государственного архитектурно-строительного университета. - 2007. - № 3. - С. 82-85.
Джарроуш, Д. Бытовая цифровая камера как инструмент для точных геодезических измерений / Д. Джарроуш // Геопрофи. - 2014. - № 4. - С. 46-49.
Bernasik, J. Automatyzacja fotogrametrycznych pomiarów odkształceń dachowych dźwigarów hal przemysłowych / J. Bernasik, M. Sławomir // Geodezja. - 2006. - № 12 (2). - S. 141-149.
Калибровка цифровой фотокамеры с целью измерения расстояний / Е.В. Попов, Г.А. Шеховцов, Р.П. Шеховцова, Ю.Н. Раскаткин // Приволжский научный журнал. - 2015. - № 4. - С. 131-140.
Раскаткина, О.В. Методические и классификационные аспекты контроля пространственного положения сооружений башенного типа / О.В. Раскаткина // Третья междунар. науч.-практ. конф. "Фундаментальные и прикладные исследования: новое слово в науке", г. Москва, 16 мая 2016 г.: сб. науч. докл. - М., 2016. - С. 58-77.
Раскаткина, О.В. Современные методы определения параметров пространственного положения и формы строительных конструкций / О.В. Раскаткина, Ю.Н. Раскаткин // Материалы междунар. науч.-практ. конф. "Наука и образование: векторы развития". - Чебоксары, 2016. - С. 272-296.
Раскаткина, О.В. Об оптимизации фотографического способа контроля вертикальности промышленных дымовых труб / О.В. Раскаткина // Третья междунар. науч.-практ. конф. "Фундаментальные и прикладные исследования: новое слово в науке", г. Москва, 16 мая 2016 г.: сб. науч. докл. - М., 2016. - С. 78-91.
Раскаткина, О.В. О методике и результатах моделирования бесконтактного фотографического способа измерения расстояний / О.В. Раскаткина // Вестник современных исследований. - 2019. - № 1-3 (28). - С. 163-170. - http://old. orcacenter.ru/journals/modern-research/ mr.2019.01.03.pdf
Гельман, Р.Н. Лабораторная калибровка камер с большой дисторсией / Р.Н. Гельман, А.Л. Дунц // Геодезия и картография. - 2002. - № 7. - С. 23-31.
Никишин, Д.А. Методы и результаты калибровки малоформатных цифровых камер с трансфокатором / Д.А. Никишин // Изв. вузов. Сер. "Геодезия и аэрофотосъёмка". - 2003. - № 4. - С. 100-107.
Могильный, С.Г. Конструктивная калибровка цифровой камеры / С.Г. Могильный, А.А. Шоломицкий, А.А. Лунев // Изв. вузов. Сер. "Геодезия и аэрофотосъёмка". - 2011. - № 2. - С. 62-66.
Шеховцов, Г.А. О методике и результатах калибровки фотокамер с целью измерения расстояний / Г.А. Шеховцов, Р.П Шеховцова, Ю.Н. Раскаткин // Геодезия и картография. - 2016. - № 2. - С. 46-53.

Еще