Solution of the integral equation for the average cost of restoration in the theory of reliability of technical systems

In the mathematical theory of reliability, when studying recovery processes, the numerical characteristics associated with the random number of failures and the random cost of recovery are first considered, for example, the average and dispersion of the number of failures and the cost of recovery, through which various criteria for the optimality of recovery strategies are determined.

The paper discusses models of the recovery process ( X_t , c i ) , i = 0,1,... , taking into account the cost of restoration. Where X i , random operation time with distribution functions F i ( t ) elements from I - 1 ^st to i -th failure, c i cost of i - x recovery, c ₀ - element cost, set at the initial time t = 0 , F ₀ ( t ) = 0 for a case t <  0, F ₀ ( t ) = 1 for a case t > 0 [1-4].

Let N ( t ) — be the number of failures (recoveries), C ( t ) be the cost of recovery for the time from 0 to t

N ( t ) C ( > ) = Z c i i = 0

P (N (t ) = n ) = F(n)(t) — F(n+1)( t),

F ^{( n} ) ( t ) - n - multiple convolution of distribution functions F i ( t ) , i = 1,2, . , n ,

t

F⁽ n ) ( t ) = ( F⁽ n ^{- 1 )} * F n ) ( t ) = J F⁽ n ^{- 1 )} ( t - x ) dF n ( x ) F ^{( 1 )} ( t ) = F 1 ( t ) .

For [1,2]: H ( t ) — recovery function (average number of failures)

X

H (t ) = E (N (t )) = £ F" )(1)

n = 1

S ( t ) = E ( C ( t ) ) — cost function (average cost of restorations)

X

S (t)) = E (C (t)) = c0 +£ cF)(t).

n = 1

During operation, the quality ( F i ( t ) ) of the restored elements and the cost ( c i ) of restoration may differ. This leads to different models of the recovery process [1, 3, 5–9].

The work considers the restoration process taking into account the cost of restoration of the order ( k 1 , k ₂ ) , in which the distribution functions and cost of restoration satisfy the condition: F ( t ) = F j ( t)ис, = c j , if the indices i , j >  k 1 when divided by k ₂ give the same excess [1, 3, 8, 9].

In the process under consideration, after the first restorations k 1 — 1 , a periodic process of the order k ₂ begins.

Note, that in the case k 1 = 1 we have a periodic process of order restoration k ₂ , and if k ₂ = 1 process of restoring order k ₁ .

If F i (t) coincide ( F i (t) = F i (t),i >1), or coincide starting from number i = 2 ( F i ( t ) = F 2 ( t ) , i >  2 ), we have simple (ordinary) and general (delayed) recovery processes, well studied in reliability theory.

Note that for the model under consideration, the recovery function H ( t ) has been well studied. Numerical methods for finding it have been developed, and for many distribution laws characteristic of reliability theory, there are its explicit representations [1, 6].

To find the cost function S ( t ) there are integral equations [1, 2, 10].

The purpose of the work is to obtain a solution to the integral equation for the cost function S(t) in the form of an integral representation through the restoration function H ( t ) . Such a representation will be convenient for its study and calculation in various theoretical and applied problems of reliability theory.

Representation of the cost function through the recovery function

Let us write the integral equation for the cost function S ( t ) [1, 2]

S (t ) = G (t ) + Js (t — x) dФ( k 2)( x)

for a case k >  1,

• k, + k, -1

G(t) = cо(1 — Ф,k■,(t))+ £ c.^’(t)—£c.J0F,n'(t—x)dФ(*■'(x), n =1

for a case k ₁ = 1

k ₂

G (t ) = cо(1 — Ф^ J( ‘ )) + tcnF')(‘)

n = 1

Ф ⁽ k ² ) ( t ) = ( Ф 1 *Ф₂*...*Ф _k 2 ) ( t ) -convolution       of all distribution functions

Ф i ( t ) = F k 1 _ _{1 +} i ( t ) , i = 1,2,..., k 2 . The functions Ф i ( t ) define the periodic part of the recovery process.

Let HF ( t ) be the restoration function of a simple process, let HFG ( t ) be the restoration function of the general process formed by the first distribution function F ( t ) and the following G ( t ) .

Further [1, 6]

HFG ( t ) = F ( t ) + j HFG ( t - x ) dG ( x )                      (2)

In equation (1) we make the replacement k 1 -1

S ( t ) = V ( t ) + c 0 + ^ С п ^ " ' ( t )                            (3)

n = 1

We obtain k1 -1                                                         k1 -1                      k1 + k 2 -1

• V ( t ) + c 0 + X 1 , F^M ( t ) = c 0 ( - Ф^ ■ ’ ( t ) ) + X c n F ⁽ ■ ' ( t ) + X c . F "’ ( t ) - n = 1                                                      n = 1                        n = k 1

  k 1 - 1

  - X c n 1 0 F' n ) (‘ n = 1

  
  

  t (

  - x ) d Ф ^{( k 2} ) ( x ) + J V ( t - x ) ^Jo

  
  

k i - 1                      A

+ c0 +XcnF(n)(t - x) dФ(k2)(x) • n =1                    у

Hence, to find the function V ( t ) , we obtain the integral equation

Let us make a replacement

k 1 + k 2 - 1                      t

V (t)= X cnF(n)(t) + j V (t - x) dФ(k2)(x) • n=k1                     0

V ( t ) =

( k₁ + k ₂ - 1 A

X cn ч n=k1     у

V( t)

Equation (4) will be rewritten as

t

V 1 ( t ) = Q ( t ) + j V ( t - x ) d Ф ^{( k 2} ) ( x ) ,

Q (t ) =

у ^{k 1} * ^k 2 ^-1 c F)(t) n = k1      n

E k 1 + k 2 - 1

c n=k1      n

Note, that Ф( k 2)(t) and Q (t) are distribution functions,Ф(k2) (t)- as a convolution of work dis- tribution functions, and Q(t ) – mixture of distribution functions.

Comparing equations (6) and (2), we find that equation (6) defines the restoration function

HQФ(k2) (t) of the general process specified by the first distribution function Q (t), of the second and subsequent ones Ф(k2) (t) •

Thus, and taking into account (3), (5), (7), (8)

S (t)

V ( t ) = HQ Ф ^{( k 2} ) ( t ) ,

k 1 - 1

= c 0 +X cnF(n)( t ) + n=1

( k ₁ + k ₂ - 1 A

X c n HQ Ф^и ( t ) ).

ч ⁿ = ^k 1 У

Taking into account (2)

t

HQФ(k2) (t) = Q (t ) + jHФ(k2) (t - x) dQ (x),(10)

formula (9) will be written in the form k1 -i                   k1 + k2 -i Г            t>

S(t)=cо+EcnF(n)(t)+ E cn Q(tWHф(k2)(t-x)dQ(x), n=1                   n = k1     V           0

or taking account of (10)

k! + k 2-1                    k! + k 2 -1

S(‘) = cо + E cF)(t)+ E CnIHФ'k2)(t-x)dF1''(x)).

n =1                       n = k10

We found that calculating the cost function comes down to calculating the finite number of convolutions of distribution functions and finding the restoration function H Ф ⁽ k ² ) ( t ) of a simple restoration process formed by the distribution function Ф ⁽ k ² ) ( t ) , or restoration function HQ Ф ⁽ k ² ) ( t ) .

In the practical implementation of the obtained formulas (9), (10), (11), one can use numerical and analytical methods for calculating convolutions and restoration functions, discussed in [1, 11]. We also note that the resulting formulas make it possible to study the properties of the cost function and consider various optimization problems based on strategies for carrying out the restoration process in terms of price, quality, and risk. If, for example, we take the average number of failures as quality, the average cost of restorations as price, and the dispersion of the number of failures or the cost of restorations as the risk [1, 12–15].

This work is a continuation of work [11] and it can be noted that the theorems on the asymptotic behavior of the cost function obtained in [11] are much easier to obtain using the resulting formula for representing the cost function (9).

The cost function for a simple restoration process with exponential distribution. We consider a restoration process in which only the restoration costs c i change according to the law c i = C j , if the indices i , j >  k ₁ when divided by k ₂ , give the same excess. This corresponds to the common case where failures result in full restorations, but the costs of restorations change, for example, only the price of the element changes.

Let the operating time of the elements be distributed according to the exponential law F ( t ) = 1 - e ^{-a t} , t >  0. For this case, we obtain calculation formulas for calculating the cost function.

Taking into account, that n - multiple convolution of the distribution functions of independent random variables is a function of the distribution of their sum, and that the Erlang order distribution n is the distribution of the sum of random variables n distributed according to the exponential law, we conclude that for the case under consideration

F" ) ( ‘ ) = F . , n ( t ) = 1 - e'“ E ^T dF ’ ) ( x ) = dF .n ( x ) = e "x a 7^ dx • i = 0 i !                                                  ( ’ ^{- 1} ) ^!

Ф ⁽ k ² ) ( t ) = F e,k 2 ( t ) , H Ф ^{( k 2} ) ( t ) = HF e , k 2 ( t ) , F_{e n} ( t ) - Erlang order distribution n , and [1,6]

k 2 - 1      k

^H F ek- , ( t ) = r< a t + E ¹

k = 1 ^{1 c}

k

/       -a t ( 1 - c^k )\

k(- e )

, c = e

2n i k2

= cos

Г 2n ^

V k2 7

+ isin

Г 2n ^

- a t

^HFe,k , ( ‘ ) = Г k ₂

a t

k

e

1    1 k ² - ¹

’+iE -

2 k = 1

n

2n    n sin atsin —k +—k

V k 2 7

Л

,

V

V      V k2   7

Г П ^ sin —к

V ^k 2 7

к

2 7

Now, according to (11)

^k 1 + ^k 2 ^{1                   k} 1 + ^k 2 - ¹         nⁿ t

S ( t ) = c 0 + £ cF ( t ) + £ c , —- J HF 2 ( t - x ) e x - ¹ dx      (13)

n = 1                      n = k i       ^{( n 1 )} ! 0

Taking into account (12), when calculating S (t), the integrals included in formula (13) are calculated explicitly. For example [16] pet

J e ^e x x ⁿ dx = — t в

n

When substituting

I (в, n)(t ) = J tfxx’dx = у

n

+ £ - 1) j

J = ¹ 1

t ⁿ

n (n — 1)...(n - J + 1)

в

A t^{n —} j + C .

)

n

+£ -1)j j=1 к

n (n -1)...(n - J + 1)

в j

t ^{n -} j

)

+ ( - 1) ^{n + 1}

n !

n + 1

in (13), we obtain k1 +k2 -1

S ( t ) = c0 + £ cnFe,n ( t ) + n=1

k ₁ + k ₂ - 1

+— £ c ^k 2 n = k 1

( n - 1 ) !

at! (-a, n -1)( t)-al (-a, n)(t) +

+£1ccr (I (-a n -1)( t)-e a(1 c ) t! (-ack, n -1)( t))).

We select the real part in (14):

1 - c

k

n k

i

- 2 ie k ² sin

^Л n k

к ^k 2

k ₂ - 1      k

■ £’F7

) k = 1 ¹ c

k ₂

-

k ₂ - 1

Re £

k = 1

c ^k

k ₂ - 1

= Re £ k=1

k ₂ - 1 £ k = 1

c ^k

к

- 1

I V П ₇ = y£ ^c tg r k

² k = 1     к ^k 2

2nki   nki e k2 e  k2

. nk

- 2 isin —

1 - k ₂

-

k ₂ - 1

)

k ₂

-a 1-ckv / г. e ( ) I (-ack

n -1)(t)) =

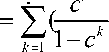
n - 1 f

+ £ 1 - ) j

J = 1 к

- 1

-

k ₂

- £ a tf

k 2 - 1 ⁱ

2a

k = 1

- a ( 1 - c k ) t

e -ac t

-a c

( t ⁿ - ¹

+

( ^{n - 1} ) ... ( n ^- j ) ( - a ) ^j c ^kj

A n -1-j

)

+

- 1) ⁿ

⁽ n ^{- 1 )!} ' ( - a ) ⁿ c ^kn )

- a t e

1 - c k

( к tn-1

n - 1

+£

j = 1

- 1

e - a t

a

nk.

1 _e k 2

. nk sin k2

n

£

k = 1

t ⁿ - ¹

к

(n -1)^(n - j) aj

c - k ( n - 1 ) e ~^a ( ^{1 -} c k ) t

1 - c ^k

—jj    a k2 tn-1-j

+

n - 1

+£

j = 1

(n -1)...(n - j ) aj

2ni,. к kj k 2   tn-1- j

+

)

-

nk.

+

( n - 1 ) ! i

2 a ⁿ

k ₂

- 1

z

--i

e

k ₂

n k ^k = 1 sin —

nk.

e

2 n k ( n - 1). i

k ₂

e

-

^{a t} e

2 n k

a tcos----

k ₂

2 n k. a tsin----i

e

k ₂

k ₂

i

2a

k ₂

- 1

e

-

a t

e

--i

k ₂

n - 1

*-1 • nk k=1 sin — v

k ₂

_i k ₂

+

2 a ⁿ

tn- ¹ + Z

j = 1

a j

e

2 n i .

kj k ₂

t^{n - 1 -} j

- 1

-

a t I

a tsin

2 n k П

+

z -

k = 1

e

k ₂

. nk sin

k ₂

Therefore

^^^^H

k ₂

- 1

— Y e-^att 2 a

n - 1

k = 1

-

( k ₂ - 1

Re Z

^^^^H

2 a ⁿ

e

-

a t k 2

2a

c ^k

’ 1 - c ^k

- 1

z

k = 1

sin

-

e

z -

k = 1

a t

e

- a

{1- ck V

⁽ ) I ( -a c k

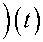
n k

n - 1

A

x Z

v k2 7

j = 1

a ^j

sin

v

k ₂

t ^{n - 1 -} j

^^^^H

sin a tsin

v

sin

2 n k

-

nk (2 n -1)

\

v

^k 2 7

n k

\

v k2 7

k ₂

Let us write down the formula for the cost function k1 + k 2

^S ( t ) = ^c 0 ⁺ Z c n F e , n ( t ) ⁺

n = 1

+--

2a

+

k ₂

k 1 + k 2

- 1

Z c

n = k

n

a ⁿ

at +

1 - k ₂

I (-a, n -1)(t)- al (-a, n)(t) +

7 „ n

-

-

a t k ₂

k ₂

V e -^at_tⁿ - 1 + e_

2a

k = 1

z

k = 1

sin

^ nk

n - 1 z j = 1

a ^j

sin

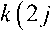
v      k ₂

t^{n - 1 - j}

- a t

+ ( n - Гуp 2 a ⁿ tf

+

v k2 7

sin a tsin

^Л 2 ~ k ^Л

v

sin

_ v ^k 2 7 ^Л nk '

+

nk (2 n - 1) 'I

k ₂

v k2 7

We also consider the cost function during the process of restoring order ( k 1 , k ₂ ) , when the operating time of the periodic part of the process is distributed according to the Erlang law of order m with a parameter a .

Let Ф j - ( t ) = F_{em a} ( t ) . We find H Ф ^{( k 2} ) ( t ) . Let us write down the integral equations for HF... a ( t ) >  H Ф ' * ‘ ’ ( t )

Let there be given

F * ( s ) = J "  e ^- st dF ( x )

*            a

Laplace-Stieltjes transform function F ( x ) [1,6]. Considering    F_{em a} ( s ) = (-----) ,

( F i * F j ) * ( s ) = F i * ( s ) F * ( s ) , from (15),(16) we obtain

H ■ F em a ( s ) = (

a

s + a

■) m + H * F em , a ( s ) (•

H *Ф ⁽ k ² ) ( s ) = (

a

s + a

-) mk2 + H *ф( k2)(s) (■

a) m, s + a a ) mk 2

s + a

Comparing (17), (18), we conclude that

H ^{ф ( k} ■ > ( t ) = HF mk 2 a , ( t ) .

We found that the restoration function of a simple restoration process formed by k ₂ multiple convolution of Erlang order m distributions with the parameter a is the restoration function of a simple restoration process formed by an Erlang order mk ₂ distribution with the same parameter a .

We have

HF e, mk2, a

i             mk 2 - 1

(t ) = —(at + У 1( ) mk2      E 1

k = 1

^HFe , mk - ⁽ t )    mk 2

a t

-

c ^k

1 - c

k ( - e ^{( 1} — c k ) ) ,

2 n

i c = emk 2 = cos

П к mk2 J

+ isin

П к mk2 J

,

mk ₂ -

- + —

-a t I

e mk2 -1

E — k=1

,             <  2 - .

sin a tsin ----k

к

к mk 2 J

+ П k ^mk 2 J

к

Now in accordance with (11)

k 1 - 1

S (t) = c0 + EcnF(n)(t)

n = 1

П sin —k к mk2 J

-I

Integral

k J + k 2 - 1 t

+ E c j F' k ¹-^ t - x ) dF ma.

n = k 1       0

(x)+

k 1 + k 2 - 1 t

+ E cn jHFe,mk2,a (t - x) e n = k1      0

-

„ ( a x ) ^{mn -1} ₄ a dx ( mn - 1 ) !

t

ГHFemk a( t - x) e a e ,mk2 ,a

^ У dx ( mn - 1 ) !

in (19) it is calculated similarly to the previous example with replacing k ₂ by mk ₂ and n by mn .

We also note that if additionally F i ( t ) = F ele ( t ) , i=1,2,..., k 1 - 1 , then F ⁽ n ) ( t ) = F_{e n}le ( t ) , n=1,2,..., k i -1 and in accordance with (19)

k 1 - 1                       k 1 + k ₂ - 1 t

^{S (} t ) = ^c 0 ⁺ E ^С Л^ ⁽ ‘ )⁺ E c J ^F. l k 1 - 1 ) l,e ⁽ t ^- x ) dF emn a ⁽ x ) ⁺

n = 1

n = k 1       0

k i + k 2 - 1 t

+ E Cn JHFemk,« n = ki 0

\ -a x

t — x) e  a

( a x ) ^{mn - 1} ( mn — 1 ) !

dx

Conclusion

The most important performance indicators of technical and many other systems are random variables [17]. These are for example the operating time of the restored elements before failure the number of failures and the cost of restoration during the restoration process. In the mathematical theory of reliability when studying restoration processes the numerical characteristics of these quantities are first considered for example the average and dispersion of the number of failures and the cost of restoration through which various criteria for the optimality of restoration strategies are determined.

Considering that the recovery function for the model under consideration is well studied the work obtained a solution to the integral equation for the cost function through the recovery function of a simple process specified by the convolution of all distribution functions of the periodic part. As a practical example explicit formulas for the cost function are obtained for the restoration process in which the periodic part is distributed according to an exponential law or Erlang law of order m with the same property a .

Note that the resulting formulas make it possible to study the properties of the cost function and consider various optimization problems in strategies for carrying out the restoration process in terms of price, quality, and risk. If, for example, we take the average number of failures as quality, the average cost of restorations as price, and the variance of the number of failures or the cost of restorations as risk.

We also note that, along with the obtained formulas for calculating the cost function, limit theorems for the cost of restorations (as a random variable), similar to those for the number of failures [3], as well as finding the dispersion of the cost of restorations in the models under consideration will also be important.