Solution of the problem of flow past a wing profile near the interface

Mo st of the pro ble ms in pote ntial th eory [1] c an generall^y b e reduced to s olving integral or integral different,»1 equationsor sets of such equations.

In the c as e of sm al l pe r^turba^tions, the soluti on t^o the prob le m co mes dow n to solv ing th^e integral equation [3, 4]

1 + 1         f 1            1                             1 + 1

2n P ( ' > 1 _ ■ " G i d s = ^- F cp । ⁵ ) ^- 2П_Р < s ) G 2 ds ’

where χ an d F ср are func tions o₂f the hy_^drofoil sh ape an_^d k_^ernels D 1 a_^n d G 2 a_^re given by G 1 = ( ^ - s ) / A ; G 2 = e/ A ; A ( ^ - s ) + e²; e = 4 h ( 0 ) . The foil shape is defined as F = F _H ± F c , where F н is th e c e n te rlin^e equ ati on a^n ^{^} d F _^ с is th e thickne ss d is t r i b^utio n. I n the fi rst ap proxim ati on of the no-penetration boundary condition we obtain:

• a)    F «( _? ) = - ■■ ^ a,^ n ,if F V ■ ■ _? n ** ; 0                   0 ^{n + 1}

MM   M

• ^b)    X "( 5 ) = ² w ( ? )1L b n ^ⁿ + 2 w ( ? ): r nb^ⁿ * >   if F c = y^ ? ⁿ - w ( ^ ) , where w = 1 .or a

sharp I^eadmg edge a^nd w = ^1-^ ² for a r^{ounded 0}nc;.

E qu a^t ion (1) is an integr al Fredhol m e quat ion of the fi rst kin d w ith a singu la^rity in its kernel

b

J k ⁽ ^, ⁵ , ^e ) Y ⁽ ^ ) d ^ = f ( ^ ) .

a

The solu^ti o n γ o f E q. (2_^) i s kn own [^6 ] t o be unstab le even at small e rro rs in f ( ξ) data and sensitive to error s in the k_^ern_^e l k (ξ , s _^) a_^n d i_^t is virt u al ly i n_^d e pen dent of t^{^}h e s o lvin g tech_^n iq u e.

T h e probl e m i^tself, (1 ) , i s es sent iall y il l - de fi n^ed an^{^}d r equ i re s pr^{^}op e r r^{^}egu lar izat ion tec hniques to enable its s ol_^u^{^}ti o_^n [^{^}6]. W h at m ak^{^}e s it il l- po se d whe n h → 0 is tha_^t in t egr al eq^{^}uat ion (1) deg enerates to a d iffe r^{^}enti al e qu atio n t^{^}h at is line ar w ith res p ec t to the hig her deriva^{^}tive. B y m ea ns o f u^n so_^phisticated mathemat ics [3, 4] integral equation (1) of the flow boundary-value problem is rewritten as

^ t 4 Y n 'ft ) *^‘ )+^ R) W ^, _{$ >}=Ф_№) , ^2П n =1 n •                     2ⁿ

^f n n (^ 2n 4 n ! ^XЙ ^{W ( S,E} ) ^,

where Ф^ ) = - F cp ( ^ ) - ±x£ W_o ( ^,8 )

1?

U ^{- 1} d U. ^;

U² + e ²

Wan (^,e)= J

-1+^

+1 Г             1

^{W ( 18} Mj vs - "

d s = ink+| ^{( 1 1})/⁸’ ^1-1 V( ^{1 + 1} )

+ 8 2

W 0 _{( 6},e )₌j _G 2 d s = a^rctgi4 + ,r^ct"-_:

+1 .„

^W ₅ ^{n (} ^,£ ) - J ( 5 — ^ ) G 2< ds, e - 4 h ( 0 ) .

F ro m E q. (3) it fo llo w s th at w he n h → 0 , prob le m (1) red_^uc es to a bou nd ary_^-layer-type problem, w hich shed s light on w hy th e p rob le m i s i ll-pos e d. The phy s ic al conditi ons impose limitation on N.

T his p rob le m can b e so lv^e d emplo^yi ng a hybr id app^roa ch. F irst, s olutio n s to the ex^ te rior, (1), and int erior, (3 ), p roblems a re found [2, 3] and then these are mutually adjusted.

T her e i s y^et a^no t^h er way t_^o ta c k l e the p ro^bl e m. It star ts wit_^h c o_^nstr^u ct i ng a pertu r^bed exterior s olutio n a nd th en t^hi s s olu_^tio n, w^hic^ h is i ll- su ited fo r h → 0, i s tr a^nsfo_^rme d s o t_^hat it is a^ble to reveal th e nat^{^}ur e o f si n^{^}g ul a_^rit y. T he r^{^}esu lta^{^} nt so lution thu s beco m^{^}es u niform ly v_^al id e ve rywhere a^{^}nd provides good app ro^{^}x im at i on to the t ru e s olu_^ tio^n. The so lu_^tion can be f_^urt^he r imp rov^ed quant itatively via highe r-o r_^de r appr oxim atio^{^} ns and, fi nall_^y, n on lin ear m et^{^}h_^ods ca_^n b e appli ed to ac celer ate c onvergence of thie functional sequence [3, 4].

If the seq^u_^e n ce is div_^erg en^{^}t, wh ich d epen ds o n th e c l as s o f th e fun^{^}c tion f (ξ) in (1), the n the linear tran sform at io ns and a lgo rithms discu ssed above allow the main t erm o f the s equen ce to b e extracted. W^ r ite t_^he sol^u^tion of i nte g r a^l eq^u atio n (1 ) a s γ = γ 1 + γ 2 . Th e fir st ter^m is a sso c iat ed with t^he influence of t he cent e rli n^{^}e sh ape on ci rc^{^}ul at io^{^}n , w^{^}hile th e sec on d o ne is at t^{^}rib u^{^}te d to th_^e dyn ami c curvature resuIting from the flow/ around a profile near tlie separation boundary.

The functi onal par am eter met hod

Represent Y 1 solution in the form of a т = 71 + 4 h 2 - 2 h series obtained t>y mapping he [ 0, ® ] toT ie [ 1,0 ] :

N

Y1" ' = E tn ,/ ".(4)

m=0 ''

Ther e is a^n e x^pansi on fo r the ker n e l w ith respe c t to pa^ra me te r τ such that:

G = £*1 mT2m ,(5)

m =1

with k 1 m defined in [3].

Se ries (5) is convergent. Moreover, it is convergent over the entire actual range of variation of the para me ter r. Conver^gence of se rie s (4^ ) remains q^uestio nabl e beca^use it is not possible to construct a general te rm . I^t is h owever p os sib le to eva lu ate a con vergen^c e d om ain for s^pecific foil shapes.

Su bs ti^tu^tin^g (4) an d (5) in^to ( 1) and r^e s olv ing th e s olu^tio n i nto two te rms (terms of the same τ power ar^e t ake n eq^ual) y ield s a s yste m of si ng u la^r in^ te gra l e qu atio^n s wi th a Cauchy-type kernel:

+1

JYn ) (s)^ = «m 1 (5), m = 0, 1, 2, ... N; n = 1, 2, ...(6)

-'      '

Co n_^ ver^{^}ting th is e quatio n in^{^} to a ∞ ⁰ cl a ss functions we have

^    fi—У ф ( n ) s )

-*■

The function Ф(т)(m = 1, 2, ..., IN) is found from the boundary conditions via the solutions y!(2„)('» = 1. 2.

.... A f - l ) . L^et us now write the solrnions tor N -13 and „ = 1 for a plate when

F cp =- ^a.

фМ=-2па; Ф«= [y«k, ^; 0            11011

^{ф 2 )}=_ 1 { ^{y10 k} 12 ₊ .« ^k 11 } d . ^;

ф^+f |^^ y«   , k,

^{- 1} ‘ ¹

Su^ bst itu^t ing ( 8) in^ to (7) gi^ves yS й)=2a'/1+1; Y1I2m)= ^m where m = 1,2 • - 13;

W = 3

• ²    2- ^^;

W = 9 - 1e - 5^ 2 - ? з .

• ⁴    8 2^s 2^{s 4;}

1 5 9   5 2   3 7 45

• ⁶    16 8^S 4^{S S} 2^{S S;}

_W = 105 - ±_{S +} 53_S 2 ₊ 43_S 3 - 21_S 4 - 15 _S 5 - 9_S 6 - _S 7 .

• ⁸    1 28 16    16      8      8      2     2       ^;

  255 217   145 2 19 3 165 4 33 5 27 6     7 11 89

W 10 = 256 ⁺ 128^ ⁺ 32^ ^- T^ ^- 8 ^ ^- T^ ⁺ T^ ^{+ 14}^ ⁺ 2^ ⁺ ^ ^;

1227 471   617

W 2 = 1024 ⁺ 256^{- е} 256^-

2 2553

3 889 4 305 5 415 6 3 7 275 8

^- - 64 ^{- +} 8 - ⁺ 8 - ^е 4^{- е} 8 ^-

45 9 13 10 ^еT^{- е}T^Y

_ξ 11 _;

W = ²⁶¹³ _е ²⁶³

¹⁴ 2048 1024 ^ξ

5825    1631    11943    10773    837    553

2 - ^е 8 - ⁺ ~W^{- +} 138 - ^е 32 - ^е 4 -

1295 8 305 9 273 10     11 15 12   13

16 ^{- +} 8 ^{- +} 4 ^{- + - +} 2 ^{- + - ;}

36297 5617

¹⁶ 32768 2048 ^ξ

20883    27063    99597

2048 -   1024 -   1024 -

6939 5

256 ξ

73617 6

256 ξ

20669     32835    53251035

7                   8              910

128 -     128 -    16 -16

е

101 11 945 12 91 13 17 14 8^ξ8 ^ξ2^ξ2^ξ

е

_ξ15 _;

4500439 2374493   81825    295437    13037

¹⁸    65536    32768 ^- 1024 ^-    2048 ^-    128 ^-

100183 5

512 ξ

25677 6

128 -

165239 7 33753 8 2049 9

⁺ 256 ^{- +} 32 ^-    8 ^-

+ 60- ¹⁵ + 129- ¹⁶ + - ¹⁷ ;

203249- ¹⁰ е 594- ¹¹ + 77- ¹² + 294- ¹³ + 187- ¹⁴ +

w =

^W 20

12616275 5179823, 262144   65536 -

8336061 2

65536 ξ

5550025 3

32768 ξ

е

3159457 4

8192 ξ

е

- ⁵ +

1024 -

+ ------- С13 е  

1024 -4

е

1151 _ξ 15 2^ξ

е

2223 - 16 _е 153 _- 17 _е 21_- 18

8 -    2 -    2 -

е

_ξ 19 _;

132266203353 317275015003   158781624145    28124698217

• ²²      131072        262144   ^-     131072   ^-      16384   ^-

  112600162755 4 67212868461 5 420259071 6 2705060269 7 2688570425 8

65536   -     32768   -     2048 -     2048   -     2048   -

80850475    41139813    6691095    5094639

+--------- - 9 +--------- - +-------- - ¹¹ +-------- -

265 -     128 -     256 -     256 -

299933 13

64 ξ

66759 14

16 ξ

1085- 15 + 20835- 16 + 8091- 17 + 1575- 18 + 95- 19 + 23- 20 + - 21 .

17129979402909 1241572992573   1889838437643 2 1355616985531 3

24      4194304         262144    -     524288    -      262144    -

+

+

262144 58073081641

4 396503371015 5 388978944203 6

-      65536    -      65536    -

8 116789059 9 337015355 10

-     512   -      512   -

4595813 64

13185 19 8^ξ

13 612715 14

- е l^-

16 ξ15

9434469 16

128 ξ

-U е

32768 28915279

- +

- l ⁷ е

45135 18

16 ξ

- 1 ² е

4301 20   231 21   25 22    23

8ξ 2ξ 2ξ ξ;

If w^e do no^t go be^yond line arized form^ ulation of t^he prob lem, then with (4) an^ d (^9) we can find the r esul^tant aero dyna mic character istics – the lift force and pitch in^g mo me^ntum c oeffi cients – using the follow ing formula s

+1

+1

C y n ) = J Y ( n ^; C M ) = J Y ( n ) ( ⁵ ) ⁵ d s •

-1

-1

I n the first bo u ndar y condition s a^p^p r^o^x im a tion , at n = 1 w^{^}e g e t t^{^}he fun ctio ns o f influence of the distance parameter h ^{( 0 )} on c P and C S in the form of Meries:

( 1 ) c y    1 . _ . 1      3    . 23 -4.11s. 39

V V =        1 + е + — е ² + _те 3 + ^е ⁴ + ,,+ + ,,е ⁶

с Y2          ^{2     4     32     16     64}

₊ 161_е 7 ₊ 5491_е 8 ₊ 256    8192

2244877 9 5379225 10

⁺ 32768 ^{е -} 65536 ^е

е ¹³ + ...;

,O'- c M * ^M " C E

= ¹ + 2⁸ + 2⁸

7   3 15 4 15 5 29 6 899   7

⁺ Гб ^{8 +} 32^{8 +} 32^{8 +} 64^{8 +} 2048 ^{8 +}

3587 8 192315 9

⁺ 8192^{8 +} 163 84 ⁸

—

1604301 10 128261286621 11

6536 ^{8 +}     524288    ^{8 +}

2091064690271    4259769570263

+_____________8 + _______________

8 13 + ...,

where 8 = t 2 ,C W = 2na, d =- na. m^

Under form al application of tlie discussed method, the solution y given by (4 )(9) is .

unstable [6]. It is considered th at a coarse so lution can be obtained talcing just a few terms of the series; a fur ther increase in the number of terms will only enhance the instability a nd the resultant multi-term series will hiave nothing to do with the true solution of Eq. (1). If however this instability is treated as a fransient pr oce ss, then it can be assetied tHat rncreasing the number of approximation terms provides additional in formation on the behavior of the true ^soluti^on.................. _.

Let ψ(^{^}ε^{^}) be a^{^}n anal^{^}y tic al functio n, th en e xpress ion (1 1) ca n be t^{^}re ated as a Taylor-serie s e xp ansion. The asym^{^}pto tic beha^{^}v ior o f c oef^{^}ficien^{^}t s o f this e x^{^}p ans ion ψ = Σ a n ε ⁿ i s d^{^}et erm ined by the typ e of the ^function sing^ularity. So itis natural to look ^for a way ^{to d}ed^uce singularity parameters from a limited sequence { a n } оf coefficients of the series [7].

The rad ius of convergence оf tile Taylor se ries is determ ined by the si ngParity of the function V(e) that is closest to the pct int a round which expansion is perform ed. Farther aw aw singularities may appear to influence the behavior of th e series coefficients as well. If th is is the case, one should find the spectrum of singularities.

The algorithms c o nside red abo ve offer a sol^u^tio n to the pr o^bl e m of ψ(ε) synthesis.

Numerical solution of Eq.(1).

In^tegral equ atio^n (1) can be solved by reducin^g it to a set of algeb r aic e q^ uations (disc rete singular ities meth^od, collocati o^n m etho d an^d o^thers) . Th e me ntion ed m ethods are st^rongly unst able [6] as t^hey use c onv entional q^ua d rature fo rmu las. At^t em^ p^ts to im^p ro^ve the resu lt b^y incr^easing the number of n ode s when ε→ 0 o^nly aggra^vate the situa^tio^n .

S olution of sin^gu lar ity equatio n (4 ) reli es on reg ula^ri zation te chn iques , he n ce a prop er c hoic e of regulariza^tor can e ssent ially enha^ nce stability of the computation scheme.

The structure of the solution y ( ^ ) = ^( 1 - ^ )/( 1 + ^ ) "^v ( ^ ) , where u ( ^ ) is a non-zero regular functi on for ξ = ±1, is d^eter mined b^y a sp ecific b eh av ior of the e dge fl ow. Aft e r s^ubstitu^tion of this so lution i nto (1) a^nd som^ e simp le m anipu lati ons we ha^ve

- 528 -

. ^2 +,' 1-S V

=^ф ( 5 ) •

where _Vft d ) = 1b and Ф (« is the ng™ side ofEq (1).

With t^h^ e n o des, re ference p o ints a^nd qu a drature co ef ficients cho se n by t^he f^o r m^u l as

^.=cos6,; sj = cos6j ; 6, = n(2i-1)/(2N + 1), (i = 1, 2, ..., N) ; 6j = 2nj/(2N + 1); Aj = 2n jvS/(2N+1) , (j = 1, 2, ..., N), we get the f^ollo^win^g se^t o f alg e^br a ic e q^u a^ti ons

^               ,

V A i j Y j = b i , ( i, j = 1, 2,..., ^ is the number of nodes), y =i ’

(12^)

whe re

Ai ■ = V ( ^, E^s )/ ( ^- " s_y ) ^; ^= ( ^{1 -} s y ) v ( s^ ( 2 A T+ 1 ) ^;

b = ^- F cp &)/^s 2 ^- g ^{x ( s )} VM ^v №’ s j ,^£ ) /^{s( 2)V + 1 ) ; V} = ^{V A ; A} = ⁽ ^ i ^- s , + s ²

Aerodynamic characteristics of a foil are de rived from formulas (10). Switching to the quadrature form11 las gives

NN

C y = 2л £ Y j and C„ = 2л £ j .                                  (13)

j = 1                                j = 1

The BCF algorithm is a powerful tool to handle integrals and resolve sets of algebraic equations due to the: quadrature and cubature formulas

1- AX AX . . i; ^^ sn      A n , 1; i^ n +i...      n + k		z 1 z 2	-	X n X . + 1
[ 1;^ n + k. • . A X n + 2 k — 1 J		[ z k + i J		Xn+k L n + k J

On ce (1 5) has be en solved, trans formatio n fo llows th^e formula

° k , n - ¹ ( z l ⁺ z ^{2 +} ••• ⁺ z k +1 ) •

T h e Т k, n transformation is implemented using the following system

^A; A n In ;.„;AJn^{k - 1}

Y 1 Y 2	=	Г S n 1 S n +1
..... Y k +1		S n + k

1; A n ₊p A n +i/ n + 1; •••; A n + 1/ ( n ^{+ 1} ) ^k '

...................................................  _k .

¹;A n + k ;A n + k/ ^{n + k} ; ™Л + k /( ^{n + k} )

where An = ASn, An = nASn, An   ASn АSn+1 /А2Sn  for Levin’s t-, w-, and v-transformations, respectively          .......... . . .

Actually, we can limit ourselves to finding only the first two components of solutions, z 1 and Y 1 , as the rest k components a re required for analysis of the transformation spectrum.

Transformation of divergent sequences a nd senes

If solution of Eq. (1) has been obtained in the form of a series, the sequence y^2m) (m = 0, 1, 2, ...), as a rule, is divergent. Summation of such series and sequences is done using 1- n                                                                                         v at                                    .-, nonlinear transformations. Since representation Sft ) = S + t ake k , where ak is an arbitrary complex number holds for {Sn}, then by analogy with the Fourier-series, the Fire summation is appUed:

° n=1 tSk- n ₁

( 18)

For th^ e series

σ

n

n

=t

i —0

n i ' '

a_i ε ⁱ .

Sometim e s we kn ow the lo ca tion of the si ngu larity [1] , gi ving ris e to div erg ence of t^{^}he ser ies, on the axis or tn the domain of variation of the parameter E. A t d i vergent series can be converted into an absolutely or conditionally convergent one by introducing some other comparison function. The Euler transformation [8] s — еД1 + s ) (s e ^ 0,0 . 5 j ) applied to tlie series in (11) уields new se ries

-=tH'€"_•k where A a 0 = a1 - a 0;  A2a0 = a 2 - 2 a.+ a 0; ...;  A ka 0 = t^€ k _/i -1) ck; A k is the operator of finite differences of order k, and Cj are ihe binomial coefficients. Reiterating the procedure s = e/(1 + s) it is 1.. • k                                t                                          .

feasible to eventually obtain a uniform app.roximation for the solution at the extremes of the specified interval h . The source series is to be rep resented in the form - = t (- 1)k ^a ksk.

^k =0                                  (

A. fter grouping the terms witf i the same power e and dropping the terms of order' O ( s N ) we ^fina lly obta'n the ^{following ap} pro x^imi^ating ex presstons for- the ^{foil lif}i force and ^pitc h m^g mi omentum as an in fluence function of the h i nterval at small angles of attack:

3 , 11 ,

^W o ² . 4 .

1 75    177    1423    11323    715923

---£4 +----£5 +-----£6 +------£7 +

32     16     64      2568192

+ 7870829- 9 ₊ 56910769-ю , 530324997219-_n , 30926120625699- 12 ₊

32768 £    65536 £      524288   £       2097152

18 879 734 589 79 33 1 13

1         31

W _M = 1 + -£ + £ 2 + — £ 3

2       16

121 4 239 5 951 6 6 0 6 7 5 7 483543 8

+--- £ +--- £ +--- £ +----- £ +------ £ +

32     32     64     2048     8192

21089 39    20321375    128639927981    7737516436603

+--------- £ 9 +---------- £ ¹⁰ +--------------- £ ¹¹ +----------------- £ ¹² +

163 8 4       65536         524288          2097152

+ 240090786810 83_B ..

While these series ; Ei re slow to converge for large h , tlicy are uniformly vailid in a larger ^dOman TkaeMe wh^en nonlinear mett l ods of convergence aeeeleration are emptoyed even Aitken’s transformation can yield the best approximation, with an accuracy of up to 23 significant figures for h e [ 0.02, 0.1]. Tlie accuracy improves for l; i rger h .

Let us now write an analytical ex pression for the sequence □ „( n = 0, 1, 2, ..., N-1) derived „_,             l ll from the. series Y = £ am£ m.

k

Constructing a sequence of partial sums and substituting it into ( - 1 ) А ^k S _n >  0 ,

..                       .               ..fi.

where Аk = ^l (-1) l Ck is the operator ofcentral difference of order k, Ck are the binominal coefficients, ive get

'an..

w^here 6 0 = a 0 a „; b = a^aa _{+ 1} ; ....; b m = a_ma n - a .^.

If in (21) an - a„+,E 0, then the nominator of the fraction should be examined for zeroes. i n n+1

Suppose, there is кр =a _n(a _{n + 1} among the polynomial zeroes; th is defect can be readily cured. When е_кр is a pole, we should set o 1 _n = o 1 _{n - 1}. Sometimes uppiearance of a pole indicates lie limits of series convergence. Thus for the vj/. series from (11) these are £ кр = a_n/a_{n + 1}, whichi agrees with the results byo^erWchniques [³. 4]                      ......

T h e a m o^u nt o f i nform a^ti on t ha^t ca^n be d^ erived for a give n nu mber of appr ox imation s does n ot l                                .■                            : l                                                                 .l appear to be enough for a transform a tion to ensure the blest approximation over the entire do main of variation of parameter e. We then have to approachi the true solution via various transformations for each h value.

The Shan ks-Sch midt-Levin trans formate ns a re based on rational approx im atioii of the series ^ akxk. Thiey complement each other as their re presentation error is associated with the Loran-series expansion of the function да                да

у( z ) = ^ a k Z k + £ b k Z ^{- k} .

k =0          k =1

Th e first term in (^22) ref^e rs to erro rs u^nde r Shank s and second one under L evin transformations. In a g enera^l c as e , i^t i s nece ss a^ry to h ave avai lable t^he se tra^nsformatio ns alo ng with the recursive techniqu^e s for t^heir e^v alu ation to b e able to a^u^to m atic al ly monitor t^he situ ation . If it appears that the

Shanks transformation fails or is slow to converge for n_t ^o , i.e. ( о _k n then switch to the Levin trans fo rma_^tion.

^^^^^^е

о, „ > s , we should ^k , ⁿ i -1-1

If Fire summation (19) is a^pplie d to se ries (11 ) and (20^) follow e d b^y sum m at io^n fo r e ach h using Shanks-Schmidt and Levin’s algo rithm s the^n t^he resu lt we obtain will a gre e w ith tha^t o f n^umeri c al simulation. The best analytic app roxima^tions emplo^ying t^ran sf^o^rm at ion of σk n se rie s (^2 0) a^ r^e ob tain e d , with rational fractions σ1, 3; σ1, 6; σ2, 7; σ3, 5; σ3, 8. The figure shows the influen ce function ψY as ev aluat ed by (11). Also shown are the results of Fire s u m mat ion appli ed to se rie s (2 0) fo llow ed b y sum ma^ti on using the Shanks-Schmidt-Levin algorithm. Com^ putat iona^l results base d on th is a l^gorith^m a^re in very good agreement with the numeric al result for inte g ral equa^t ion (1) solv^ed by the c ol loc a^t ion t ech ni que using BCF apparatus as prescrib ed by t^he given al gor ithm. T h^e f^ou r-term expa^nsi^on ψY f^rom (1 1 ) is uniformly valid over the interval h e(hp\ h^), the quantitative result, however, being far from exact.

Conclusion

Optimal asymptotics contains nine terms, and still it rapidly deviates from the exact solution; however an approximation such as σ 3, 8 for h < 0,01 already gives a relative error less than 1 %.

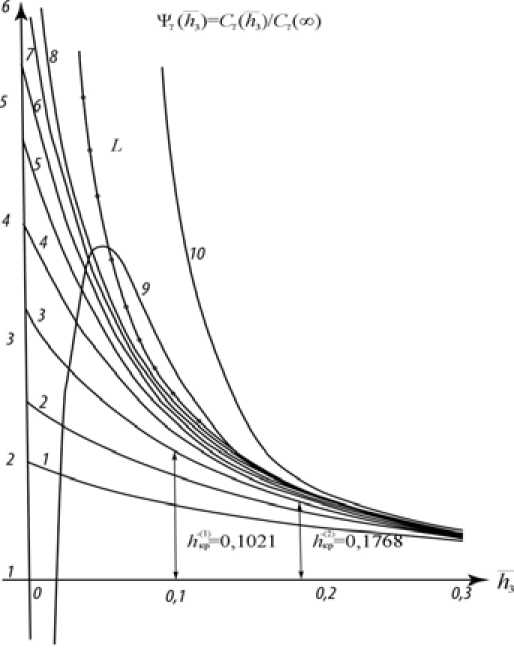
Fig. The function of influence of h interval on the lift force: L – influence function derived from (20) using Levin’s tr an sformatio n for eac_^h h – N_^umer ical s imula_^tion resu lts for Eq. (1) o btai ned b_^y t_^he collocation method using Де BeF apparatus

The discussed algorithms have been implemented as computational programs for algebraic (ALFA) and integral (OMEGA) equations, ordinary (SIMP) and improper (SECOB) integrals, including the Cauchy integral (DSECOB) as well as summation programs for sequences and series (SHENKS, AYTKEN), including divergent ones (EULER).

The reported study was funded by Russian Foundation for Basic Research, Government of Krasnoyarsk Territory, Krasnoyarsk Region Science and Technology Support Fund to the research projects № № 17-48-240386 р_а and 16-41-242156 р_офи_м.