Some interrelations in matrix theory and linear algebra for quantum computing and quantum algorithms design. Pt. 1

The goal of this pedagogical article is to describe for IT engineering researchers and master course students main mathematical operations with matrices and linear operators used in quantum computing and quantum information theory. These operations are defined in the framework of linear algebra and therefore for their understanding there is no need to introduce physical background of quantum mechanics.

Matrices have been the subject of much study, and large bodies of results have been obtained about them. In this article we introduce main definitions of matrix theory and study the interplay between the theory of matrices and the theory of orthogonal polynomials. Interesting results have been obtained for Krawtchouk polynomials and also for generalized Krawtchouk polynomials. More recently, it was obtained conditions for the existence of integral zeros of binary Krawtchouk polynomials. Also it was obtained properties for generalized Krawtchouk polynomials. Other generalizations of binary Krawtchouk polynomials have also been considered. Generalized some properties of binary Krawtchouk polynomials to q-Krawtchouk polynomials, derived orthogonality relations for quantum and q-Krawtchouk polynomials and showed that affine q-Krawtchouk polynomials are dual to quantum q-Krawtchouk polynomials. In this paper, we define and study a generalization of Krawtchouk polynomials, namely, m -polynomials [1-4].

Definition of a partial matrix . A partial matrix is an array in which some entries are specified, while the remaining entries are free to be chosen (from a certain set).

We make the assumption throughout that all diagonal entries are prescribed.

Definition of a completion of a partial matrix . A completion of a partial matrix is the conventional matrix resulting from a particular choice of values for the unspecified entries.

The completion obtained by replacing all the unspecified entries by zeros is called the zero completion and denoted A .

A matrix completion problem asks which partial matrices have completions with a given property.

Definition of totally positive (nonnegative)/negative matrices . A matrix A is called totally posi-tive / negative (P/N) if all the minors of A , of all orders are positive/negative.

A square matrix M is called P -matrix if all principal minors of M are positive, where a principal minor of a square matrix M is the determinant of a principal sub-matrix that is formed by arbitrary rows and the corresponding columns of M .

Example . Let

- 3

- 1

- 2

.

Considering det (1) = 1, det (4) = 4, det ( 6) = 6, det

( 4

0 )

v—1  6

= 24, det

6 J

= 16,

det

_v - 3

0 )

4 J

= 4, det M = 58 ,

we see that all principal minors of M are positive. Therefore, M is a P -matrix.

The set of all P -matrix is denoted as P . P properly contains two important subclasses of matrices.

First , P properly contains all positive definite matrices, where M is called positive definite if X T Mx >  0 for all x e R ” , x * 0 . We denote the set of all positive definite matrices by PD .

Second, P properly contains all H-matrices with positive diagonal entries, where M is called H-matrix if the comparison matrix M = (ctj) defined by cu =

- mj  f'i * j

is a P -matrix.

We denote the set of all H-matrices with positive diagonal entries by H ⁺ . If all off-diagonal elements of M e H⁺ are non-positive (negative), then M is called a K-matrix (usually, such a matrix is also called an M -matrix, see below).

Example . For the special case that M is symmetric and all off-diagonal elements of M are nonpositive, the following holds:

M e PD ^ M e H⁺ .

In general, however, PD ^ H⁺ and PD ^ H⁺ .

Definition of Z- matrix . The square matrices whose of-diagonal entries are nonpositive are called Z-matrices. Using the definition of Z-matrix is possible define the Fan product.

Example . Let A and B be Z-matrices. The Fan product C = A@B is defined as follows:

^c j =A

а « Ь ц for all i = j

.

— a..b.. for all i * j ii ii

Definition of comparison matrix . The comparison matrix M ( A ) = ^ m_tj J of a given complex matrix A = ( а^ ) is defined by m_y = | a _zy | if i = j and m_y = - ^а^ | if i * j and that A is an H-matrix if M ( A ) is an (invertible) M -matrix.

Thus, the Fan product of two Z-matrices is really the comparison matrix of their Hadamard product.

For a square matrix B we let p ( B ) the spectral radius of B and, for k = 1,2,..., n , let p ( B ) denote the maximum radius of all k x k principal submatrices of B . It is well-known that, if B >  0, then 0 <  p ( B )<•••< p_ _г ( B ) <  p ( B ) = p ( B ) and that the latter inequality is strict if B is irreducible.

For s = 0,1,..., n , let L_s denote the real n x m -matrices which have the form:

A = tl - B, where B > 0 and p (B) < t < p^! (B) (here, for completeness, p (B) = -^ and p^j (B) = +^). These matrices form a partition of the Z-matrices and the familiar (invertible) M-matrices (matrices of the form A = tl - B where B > 0 and t > p(B)) are properly contained in the class Ln .In fact, Ln is precisely the class of general M-matrices (as mentioned above, matrices of the form: A = tl - B , where B > 0 and t > p(B)). We let K denote the invertible M-matrices and K the general M-matrices. Since a Z-matrix is in L only iff all of its principal minors of order k or less are in K , we see that if A is in L , then C = A@B is in Ls where m > min{s,t} .

The definition of the Perron complement and its interrelation with Schur complements . Let A = ( a_tJ ) be an n x n matrix, and a , в be nonempty ordered subsets of ( n ) : = { 1,2,..., n } , both consisting of strictly increasing integers. By A [ a , в ] we shall denote the submatrix of A lying in rows indexed by a and columns indexed by в . Similarly, A ( a , в} is the submatrix obtained from of A by deleting the rows indexed by a and columns indexed by в . If, in addition a = в , then the principal submatrix A [ a , a ] is abbreviated to A [ a ] , and the complementary principal submatrix is A ( a ) . For any n -vector, x and a c ( n ), we let x [ a ] denote the subvector of x whose coordinates are indexed by a .

Let в c ( n ) . If A [ в ] is nonsingular, then the Schur complement of A [ в ] in A is given by

S ( AIA [ в ] ) = A [ a ] - A [ a , в ] ( A [ в ])" * A [ в , a ] , where a = ^ n ^ \ в . Schur complements have been well studied for various classes of matrices, including: positive definite, M-matrices, inverse M-matrices, and total negative (TN) matrices. In particular, it is known that the classes of positive definite, M-matrices, inverse M-matrices are all closed under arbitrary Schur complementation.

Remark . In particular, if A is a nonsingular M-matrix, then (all) its Schur complements are M-matrices. If, however, A is inverse of an M-matrix, then again, as is well known all its principal submatrices are invertible and the inverse of its Schur complements are M-matrices by virtue of their being principal submatrices of A ^{- 1} . The inverse of the principal submatrices of A are M-matrices because they are Schur complements of A ^-1.

Meyer (in “Uncoupling the Perron eigenvector problem” // Linear Algebra and Its Applications, 1989, Vol. 114/115, No1, pp. 69-94) introduced, for n x n nonnegative and irreducible matrix A , the notion of the Perron complement .

Again, let в c ( n ) and a = ^ n ^ \ в . Then the Perron complement of A [ в ] in A is given by

P ( AIA [в]) = A [a] + A [a, в]( p( A) I - A [в])"* A [в,a],                 (1)

where p ( - ) denotes the spectral radius of a matrix.

Recall that as A is irreducible and nonnegative, p ( A ) >  p ( A [ в ] ) , so that the expression on the righthand (1) is well-defined.

Useful properties of P ( AIA [ в ] ) ^: ( i ) The first is that p ( P ( AIA [ в ] ) ) = p ( A ) ; ( ii ) The second is that if A is row stochastic, then so is P ( AIA [ в ] ) - 0 •

Observe that the matrix ( p ( A ) I — A [ в ] )   is an inverse M-matrix (by the definition).

If A is an inverse of an irreducible M-matrix, then its Perron complements are (also) inverses of M-matrices.

A slight extension of the notion of the Perron complement . For any в ^c ( n ) and for t - p ( A ) , let the extended Perron complement at t be the matrix:

P t (AIA [в]): = A [a] + A [a, в] (tl — A [в])—1 A \вО\,

t ^- p ( A ) > p ( A И) •

which continues to be well-defined since

Interrelation with Schur complements . The Perrron complements of A are inverses of M-matrices and the inverses of associated principal submatrices of A are “sandwiched” between the inverses of the Perron complements of A and the inverses of the corresponding Schur complements of A . The extended Perron complement at t , P_? ( AIA [ в ] ) , is an inverse of an M-matrix and the following relation: ( P_z ( AIA [ в ] ) ) < ( A [ a ] ) < ( S ( AIA [ в ] ) ) , where, as before, a = ( n ) \ в , with ( ^P t ( A ^I A [ ^в ] ) ) being an entry-wise increasing matrix in [ p ( A ) , ^ ) for which lim ( P t ( AIA [ в | |) ' = ( A [ a ] ) • We can thus view the M-matrix ( A [ a ] ) as separating between the M t ^^

The situation is slightly more subtle for TN-matrices.

Definition of sparse matrix . A matrix is sparse if the number of its zero elements is much less than the size of the matrix itself.

Definition of reducible and irreducible matrices . Let A = ( a_tJ ) be a ( 0,1 ) -matrix of order n and let I_n denote the set ( 1,2,..., n ) . For given subsets a and в of I_n , let A [ a , в ] be the submatrix of A consisting of all rows numbered a. , a ^E a , and all columns numbered в , в ^E в •

Matrix A is said to be reducible if there exist nonempty subsets a , в of I_n such that:

Otherwise, A is irreducible .

Equivalently, A is reducible if there exists a permutation matrix P such that: PAP^T =

( B

where

• B,    C and D are square matrices.

Remark. Matrix A is the adjacency matrix of a digraph (directed graph) G with n vertices and d arcs. A is irreducible iff its digraph is strongly connected. A primal subgraph of G is the graph obtained from G by deleting one vertex, say i , and all the arcs going out from i or into it. The adjacency matrix corre- sponding to this primal subgraph is the principal submatrix A of A obtained by deleting row and column i of A .

Example . For a given ( 0,1 ) -matrix A = ( a_tJ ) of order n , satisfying a_u = 0 , i = 1,2,..., n , we denote by s ⁰ ( A ) and s 1 ( A ) , i = 1,2,..., n , the number of the off-diagonal 0’s and 1’s, respectively, in the union of row and column i of A , and by s ( A ) we denote the total number of 1’s in A . Obviously,

n si (A) + si (A) = 2(n — 1), i = t2,---,n , s(A) = -£si (A).

² i = 1

² i = 1

If s (A) > [n (n — 1) /2] +1, then there exists at least one irreducible principal submatrix A of A . If all the principal submatrices of A are reducible, then: s0 (A) > n — 1, i = 1,2.

Indeed, let

Г о

Thus, A is reducible, but all A are reducible.

Definition of spectral radius of a matrix . The spectral radius of an arbitrary real matrix A , denoted

A

p ( A ) , is defined to be: p ( A ) = max { 2 : 2 is an eigenvalue of A } . According to Browne s theorem, p ( A ) >  a _min ( A ) , where a _min ( A ) is the minimum singular value of A . The lower bounds are as follows:

[P( A)]2 > Otn (H) — OL ( S) + 2b2, [p( A)]2 > Omrn ( S) — Omax (H)+ 2a a where H and S are the Hermitian and skew-Hermitian parts of A, amax( X) represents the maximum singular value of X, and a = a + jb is an eigenvalue of A such that p ( A) = |a|.

Example . The spectral radius of a symmetric, positive semidefinite matrix of rank m is

A

^where H A I L = E ^a 2 j is the Frobenius norm of A . If A is a real matrix such that rank ( A ) > 2, then for

i , j

Tr2 (A ) — Tr ( A2)

If Tr ( A ² ) > — Tr² ( A ) , the

m

Tr ( A2) — — Tr2 ( A )

If rank ( A ) = 2 , then both are equivalent.

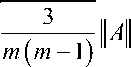
If A skew-symmetric then p ( A ) >

We introduce the operation definitions of four matrix products, namely the Kronecker , Hadamard , Tracy-Singh and Khatri-Rao products, and then give the definitions of several equalities the Trace-Singh and Khatri-Rao products.

Types of matrix products . Firstly, we repeat the definition of standard matrix product. In this case the product of matrices C = AB is defined correctly by the condition that the number of columns of matrix A is equal to the number of rows of matrix B .

T1. Standard matrix product. For matrix A = ( ay) of order m x p and matrix B = ( bkz) of order p x n the standard matrix product in linear algebra is defined as following: C = AB, where cy = ^ aikbkj k and i = 1,2,...,m; j = 1,2,...,n .

Remark . In more general case the number of columns of matrix A can be not equal to the number of rows of matrix B . For these cases must be defined another types of matrix products.

T2 . Kronecker , Hadamard , Tracy-Singh and Khatri-Rao type products . Let us consider matrices A = ( a_y ) and C = ( c_y ) of order m x n and B = ( b_kl ) of order p x q . Let A = ( A ) be partitioned with A of order m _z x n as the ( i, j ) -th block sub-matrix and let B = ( B _z) be partitioned with B_{k z} of order p_k x q _z as the ( k, l ) -th block sub-matrix ( ^ m _z = m, ^ n. = m, ^ p_k = p, ^ q = q ).

The four another matrix products of A and B are defined in Table 1 as follows.

Table 1: Matrix product’s types

N	Definition of matrix product
1	Hadamardproduct : A©C = ( ac.. ) = ( ac. ) , ij ij ij              ij ij where a.,c.. and a.c.. are the i -th scalar elements of A = ( a. ) , C = ( c. ) and A©C , respec- ij     ij                  ij ij                                                                                                   ij                         ij tively, and A, C , and A 0 C are of order m x n .
2	Kronecker product : A 0 B = ( ayB ) = ( ayB ) , where ay is the ij -th scalar elements of A = ( ay ) , ayB is the ij -th sub-matrix of order p x q and A ® B is of order mp x nq .
3	Khatri-Rao (column wise Kronecker) product : A® B = ( A ® By ) = ( Ay ® By ) , where A is the ij -th sub-matrix of order m( x n y., By is the ij -th sub-matrix of order pt x q. , A„ ® B. is the ij -th sub-matrix of order msp, x n^, and A®B is of order r x 5 ( r = 7 m.p. ij        ij                                                            i   i      j j                                                                    ii and 5 = ^ nyq j ).
4	Tracy-Singh product : AMB = ( AyMB ) = ( ( A ® Bk /)й ) = ( AyMB ) , with A^B = ( A ® Bk ;) , where A is the ij -th sub-matrix of order mt x ny , Bkl is the kl -th

sub-matrix of order pk x qf, A. 0 Bkl is the kl -th sub-matrix of order mtpk x njql, A^^B is the ij -th sub-matrix of order mtp x n.q and AMB is of order mp x nq .

Thus the operations { (•) ,0, 0 ,®, Kl} define standard , Hadamard ’s, Kronecker ’s, Khatri-Rao ’s and Tracy-Singh ’s products, correspondingly.

Remark . The definition of Tracy-Singh product is to place A^B_U = ( A BB_{k z}) as the ( k, l ) -th block sub-matrix of AMB . For a non-partitioned matrix B , their Tracy-Singh product AMB is A 0 B . The new definition advocated above of the Tracy-Singh product is different and is given by Liu (1999) in such a way (similar to that the right Kronecker product is defined): A И B = A 0 B_kl is located as the ( i, j ) -th block matrix. In fact, the theorems to be presented in the sequel remain the same for the two definitions, which link each other, of the Tracy-Singh product.

Example . For non-partitioned matrices A and B both AB and AB yield the Kronecker product. For C = ( c_tJ ) where c_y is a scalar, we have

C ^B = ( c , ■ ^B ) „ = ( ( c . ⁰ B kl ) kl )„ = ( B ) , = ^{C 0} B and '    B = ( cB , ) .

which can be viewed as a generalized Hadamard product.

The following connection between the Kronecker’s and Hadamard’s products is observed by Faliva : J T ( A 0 C ) K = A 0 C , where A and C are the same order m x n , in general; J is the m ² x m selection matrix and K is the n ² x n selection matrix.

The case, where J = K with m = n is correlated with well-known several matrix Kantorovitch-type inequalities.

Let us consider another type of matrix product as Fan product of M -matrix.

Definition . A square n x n matrix A is called a general M - matrix if A can be expressed in the form

A = sI — P with P > 0 , where s > p( P), the spectral radius of nonnegative matrix P. Thus M -matrices consists of nonsingular M -matrices and singular M -matrices.

Remark . As usual, a matrix A = ( a_tj ) is nonnegative if each a_y >  0 , and positive if each a_tj >  0 , denoted by A >  0 and A >  0 , respectively. A matrix A is an M-matrix if each a_y <  0 .

For two general M -matrices A = ( a_tj ) and B = ( b_tj ) , the Fan product of A and B , denoted A©B , is the matrix C = ( c ) where c.. = a b.. for all i and c.. = — a b.. for i ^ j .

ij                          ii          ii ii                                     ij              ij ij

Types of matrix inverses : The weighted Moore-Penrose, Drazin and Group inverses . The representation for the weighted Moore-Penrose inverse, the Drazin inverse, and the group inverse of the Kronecker product A 0 B of the two matrices A and B are considered, and by using these results, the determinant forms for projectors are deduced.

Let A e C ^{m x n} , and M and N be positive definite matrices of order m and n respectively.

Schur complements and its generalizations have many applications in numerical mathematics. Our goal is to derive known ones by a different procedure (that could be extended to the vector case). It has been evident that Schur complements are a powerful for deriving matrix inequalities and further in deducing determinant, trace, norm, eigenvalues, singular value, majorization, and other matrix inequalities. In particular, combining Schur complements of matrices with Kronecker products of matrices, we can study their Lowner partial order and obtain some important inequalities. The purpose of this part is to present a matrix inequality on the Kronecker product that unifies the proofs of many existing matrix inequalities in the Lown- er partial ordering on the sum, ordinary product, and Hadamard (Schur) product. Schur complements serve as the basic tool.

Schur complements . We consider the following partitioned matrices

A =

< C D ,

f B

< D

EC

F J ' C f G

Assuming that D is square and nonsingular, we define the following Schur complements of D as ( •/ D ) in the corresponding partitioned matrix

( A ' / D ) = A - BD"’C ; ( B' / D ) = E - BD ^{- 1} F ; ( C' / D ) = G - HD⁴C ; ( D' / D ) = L - HD ^{- 1} F .

Remark. Ratios of determinant, Sylvester identity, Schur complements, and the bordering method are, in fact, all related to Gaussian elimination for the solution of linear equations. Schur complements are related to the Gaussian factorization of a matrix and indeed, fI  BD-1 Y( A / D)  0 )  ,_f I  BD - Y 0  (B' / D ^

1 0    I JI   C    D J     1 0    I J( D . f I    0 ^f   C    D ^. f I    0 ^f D C "[ HD - 1   I J[ ( C / D )   0 J , D "[ HD - 1   I J 0

F  J F  " ( D / D ) v

So, if the matrices are square, we have the Schur determinantal formulae det (A *) = det (A' / D) det (D); det (B *) = (-1) n det (B' / D) det (D);

det (C') = (-1)n det (C' / D) det (D); det (D') = det (D' / D) det (D) , where n is the dimension of the block opposite to D on the diagonal.

Example . Let A is square and nonsingular. We consider the system of linear equations

, C  D J[ y J  [ v _v .

Since D is square and nonsingular, we see from Gaussian factorization of A' (or from the corresponding determinantal formula), that ( A1 / D) is nonsingular and it follows that x = ( A' / D )_1 ( u - BD-1v ).

Once x has obtained, y can be easily deduced. Similar expressions hold for the systems with matrices B ’ , C ’ and D ’ .

Schur complements can be defined also for matrices partitioned into an arbitrary number of blocks. We consider the n x m block matrix

	f A ,,    •	A1j   .	A 1 m
M =	A ,    •	A ij	Aim
	v An 1   *	A nj	A nm J

We denote by A" i ^, j ) the ( n - 1 ) x ( m - 1 ) block matrix obtained by deleting the i th row of blocks and j -th column of M , and we set

^L1 j

A

A

’   ^Ci   ^{( A} 1 j ,*”’ ^Ai, j - 1 , ^Ai , j + 1 ’’”’ A im ) •

A

Assuming that A is squared and nonsingular, the Schur complement of A in M is

( MIA j ) = A i' ) — BA — C , .

The quotient property of Schur complements . Let us consider the matrix

( A  B  E

CDF

. G  H  L ,

.

The quotient property of Schur complements can be established using the Schur determinantal formula. We will consider a proof based on the inverse of a boarded matrix that in quantum computing is used.

Quotient Property : If ( D' ID ) is nonsingular, then

Proof of property. By definition: ( MID ') = A — ( BE )( D ') ¹

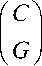
Setting for the simplicity S = ( D ‘ ID ) , we have, by the block bordering method,

( DT1

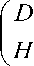
F V _( D ^{— 1} + D ^{— 1} FS ^{— 1} HD ^{— 1}

L J ~(    — S ^{— 1} HD ^{— 1}

and ( a ) follows easily from the expression of ( MID ') . We set: M '

— D ^{— 1} FS ^{— 1} '

S ^{— 1}     J

(( AID)  (B' IDp

So, ( M ‘ I ( D ' ID ) ) = ( AID ) — ( B' ID )( D ‘ I D )^{— 1} ( C ‘ I D ) = ( MID ') • But, from Eq. (1),

( MID ) =

( A v G

—

( B ^

A — BD ^{— 1}C  E — BD ^{— 1} F

G — HD "*C L — HD ^{— 1} F

= M'

which proves ( b ) .

Remark . In the case where the matrices involves are square, the expression ( b ) gives det ( MID ) = det ( M ) I det ( D ) = det ( MID ' ) det ( D' ID ) .

If A, E and L are numbers, then the four Schur complements involved in the right hand side of (a) are also numbers and Schur determinantal identity for (M I D‘) gives det (M) det (D) = det (A') det (D') - det (B‘) det (C'), which is the Sylvester identity.

The Schweins determinantal identity can be obtained by applying the Sylvester identity to the matrix

	' 0	b 1	b n - 1	bn
	0	a 1,1	* *      a 1, n - 1	a 1, n
M =	0	a n - 2,1    *	* *    a n - 2, n - 1	a n - 2, n
	1	a n - 1,1    *	* *    a n - 2, n - 1	а з n - 1, n
	0 V	c 1	c n - 1	cn

So, the Schweins identity can be seen as arising from Schur complements and the quotient property. It can be extended to the case where A , E , G and L are matrices instead of numbers.

Example . Now we consider the system

( A	B	E )	л x		л u
C	D	F	y	=	v
V G	H	L V	V z J		V w J

Let us apply the block Gaussian elimination to this system with D as the pivot.

The first step consists in eliminating B and:

'( AID)

CD

V( C' ID )

( B' I D )" F

( D' / D )v

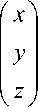
^ u - BD " 1 v

v w - HD1 v ,

Let us notice that this system leads to

The second step of Gaussian elimination removes ( B' ID ) and gives

'( MID')

CD

V( C ’ ID )

0     '

F

(D'ID),

' ( u - BD - v ) - ( B ' I D )( D' I D ) - ( w - HD v )'

w - HD 1 v

and it follows: x = ( MID ')" 1 ( u - BD ^{- 1} v ) - ( B ' I D )( D ' I D ) ^- 1 ( w - HD ^{- 1} v )

. This formula can also be

obtained directly by applying x = ( AID ) 1 ( u - BD 1 v ) . The expressions for y and z can easily be deduced. We also have

	f I	BD ■*	( В ’ / D )( D ' / D ) — '	f ( M / D ')	0	0    ^
M =	0	I	0	C	D	F
	0 V	HD — 1	I 7	v ( C' / D )	0	( D ’ / D ) ,

Let us now consider the problem of developing conditions under which generalized inverses of partitioned matrix can be expressed in the so-called Banachiewicz-Schur form . The theorem of Marsaglian and Styan, concerning the class of all generalized inverses, the class of reflexive generalized inverses, and the Moore-Penrose inverse, is strengthened and new results are established for the classes of outer inverses, least-squares generalized inverses, and minimum norm generalized inverses.

Banachiewicz-Schur form of generalized inverses of partitioned matrices. Let      denote the set of m x n complex matrices. It is known from above mentioned results that if a matrix Mo eSm+p m+p, parti- tioned as Mo =

D

, is such that A eS_{m m} is nonsingular and the Schur complement S _o e S_p of

A in M _o , defined as: S ₀ = D₀ — C ₀ A/ B_o is also nonsingular, then the inverse of M _o is expressed in the

Banachiewcz-Schur form

M 0 - ¹

^f A ¹' + a q B q S" ^— c o A "‘ ;— A — B q S Q '

_V      — SC о a —¹      =     S '

Remark. Marsaglia and Styan substantially extended this result replacing M by a general partitioned matrix M e 5m+p, n+q

of the form M =

C

and considered the problem of characterization situations

where generalized inverses of M admit similar to Eq.(3).

Let us recall that the set of generalized inverses of a given matrix K eS_st is specified by

Perhaps the best known element of K { 1 } in Eq.(4) is the Moore-Penrose inverse of K ,denoted by K ⁺ , which according to Penrose defined as mentioned above by:

L = K ^ KLK = K, LKL = L, KL = (KL )*, LK = (LK )*, where the asterix superscript denotes the conjugate transpose.

In Table 2 other classes of generalized inverses are considered.

Table 2: Types of generalized inverses

Class of inverse	Mathematical expression
The set of outer inverses	K { 2 } = { L eSts : LKL = L }
The set of reflexive generalized inverses	K { 1,2 } = { L eS .$: KLK = K , LKL = L }
The set of least-square generalized inverses	K { 1,3 } = { L e S,iS : KLK = K , KL = ( KL ) * }
The set of minimum-norm generalized inverses	K { 1,4 } = { L e S,,s : KLK = K , LK = ( LK ) * }

Remark . Namely, for any fixed generalized inverse G e A { 1 } , S eS will denote the generalized Schur complement of A in M partitioned as above mentioned, i.e., S = D - CGB , and N e S _m+p will stand for a partitioned matrix having the specific structure

' G + GBHCG v - HCG

- GBH

with H eS_{q p} u Under the assumption that H e S { 1 } , a generalized inverse of M is expressible in the for (5) iff:     F.BE_S = 0, F_SCE, = 0, F.BHCE. = 0, where E. = I - GA, F = I - AG ,      and

AS    SA    A    A           A  n     A  m

E_s = I - HS , F_s = I - SH , and these conditions are independent of the choice of G e A { 1 } and H e S { 1 } involved in the last conditions. Solutions of a similar type were given also for the problem of characterizing the cases where N e M { 1,2 } and the cases where N = M ⁺ . In addition to the problems of when N e M { 1 } , N e M { 1,2 } , and N = M ⁺ , three new problems of when N e M { 2 } , N e M { 1,3 } and N e M { 1,4 } can be solved. For these cases by combining solutions for the classes M { 1 } and M { 2 } it is possible to get a solution for the class M { 1,2 } and combining solutions for the classes M { 2 } , M { 1,3 } and M { 1,4 } to get a solution for the Moore-Penrose inverse M ⁺ .

Remark. In all conditions involved in them the choice of G e A {1} and H e S {1} is negligible. However, there is one important formula in which the independence property of this type is not valid, viz. the formula

S = D - CGB defined the generalized Schur complement of A  in M. For example, if A =

f 0

0 )

0 >

, B =

1   ,

s

uv

: s , v , u e 5 > , and hence the set

of all possible generalized Schur complements of A in M is { S = D - CGB : G e A { 1 } } = { ( - v ) : v e 5} .

This set is obviously dependent on the choice of v in the representation A { 1 } of a generalized inverse of A . If v ^ 0 , then E_s = ( 0 ) = F_s , and since F_AB = 0 and a generalized inverse of the matrix M with abovementioned submatrices is expressible in the Banachiewicz-Schur form. If, however, v = 0 , then ^E S = ( 1 ) = ^F S , ^and since CE_a = ( 0 1 ) ^ 0 , a generalized inverse of M in the form (5) does not exist.

Krawtchouk matrices from classical ad quantum random walks

Krawtchouk’s polynomials occur classically as orthogonal polynomials with respect to the binomial distribution. They may be also expressed in the form of matrices, that emerge as arrays of the values that the polynomials tae. The algebraic properties of these matrices provide a very interesting and accessible example in the approach to probability theory known as quantum probability. First it is noted how the Krawtchouk matrices are connected to the classical symmetric Bernoulli random walk. And we show how to derive Krawtchouk matrices in the quantum probability context via tensor powers of the elementary Hadamard matrix. The connections with the classical situation are shown by calculating expectation values in the quantum case.

Some very basic algebraic rules can be expressed using matrices. Take, for example,

( a + b ) 2	=	a 2 + 2 ab + b 2	^
( a + b )( a - b )	=	a 2 - b2

				ф( 2 ) =	"111 " 2  0   - 2 1    - 1    1
( a - b ) 2	=	a 2 - 2 ab + b 2

(the expansion coefficients make up the columns of the matrix). In general, we make the definition:

Definition. The N' t' -order Krawtchouk matrix Ф ⁽ N ) is an ( N + 1 ) ^x ( N + 1 ) matrix, the entries of which are determined by the expansion:

N

( 1 + и ) " ^-J ( 1 - и Г=£ и ' Ф ikN ' •   ф ( N ' ZH ) k ^k_k   .  _k ^j

i = 0                    k        V ^k /V i ^k

The left-hand-side G ( u ) = ( 1 + и ) N ^k ( 1 - и ) ^k is thus the generating function for the row entries of the j^th column of Ф ⁽ N ) . Expanding gives an explicit expression.

Here are the Krawtchouk matrices f order zero and one:

In the remaining of the text, matrix indices run from 0 to N .

One may view the columns of Krawtchouk matrices as generalized binomial coefficients . The rows define Krawtchouk polynomials : for a fixed order N , the i -th Krawychouk polynomial is the function

K i ( j , N ) = Ф ( jN ¹

that takes nits corresponding values from the i -th row. One can easily show that K _z, ( j , N ) is indeed a polynomial of degree i in the variable j .

Remark. Historically, Krawtchouck’s polynomials were introduced and studied by Mikhail Kraw-tchouck in the late 20’s. Since then, they have appeared in many areas of mathematics and applications. As orthogonal polynomials, they occur in the classic work by Szego. They have been studied from the point of view of harmonic analysis and special functions, e.g., in work of Dunkl. In statistical considerations, they arose in work of Eagleason and later Vere-Jones. They play various roles in coding theory and combinatorics, for example, in MacWilliams’ theorem on weight enumerators, and in association schemes.

Remark. A classical probabilistic interpretation has been given by Feinsilver and Schott (1991). In the context of the classical symmetric random walk, it is recognized that Krawtchouk’s polynomials are elementary symmetric functions in variables taking values ± 1 . Specifically, if ^ are independent Bernoulli random variables taking values ± 1 with probability 1 , then if j of the ^ are equal to - 1 , the i t elementary symmetric function in the ^ is equal to Ф ^{( №} ) . It turns out that the generating function is a martingale in the parameter N .

Remark . As matrices, they appeared in the work of N . Bose (1985) on digital filtering, in the context of the Cayley transform on the complex plane. The symmetric version of the Krawtchouk matrices has been considered by Feinsilver and Fitzgerald (1996).

Despite this wide research, the full potential, meaning and significance of Krawtchouk polynomials is far from being complete. Section we look at Krawtchouk matrices as operators and discuss two new ways in which Krawtchouk matrices arise: via classical and quantum random walks. The starting idea is to represent the second Krawthouk matrix (coinciding with the basic Hadamard matrix) as a sum of two operators

1   - 1

0 1  10

1  0 + 0   - 1

Via the technique o tensor products of underlying spaces we obtain a relationship between Krawtchouk matrices (Table 3) and Sylvester-Hadamard matrices.

	"1	1	1	1	1
	4	2	0	- 2	- 4
ф( 4 ) =	6	0	- 2	0	6
	4	- 2	0	2	- 4
	1	- 1	1	- 1	1

	' 1	1
	5	3
ф( 5 ) =	10	2
	10	- 2
	5	- 3
	_ 1	- 1

- 2

- 2

- 1

- 2

- 1

- 3

- 3

- 5

- 10

- 1

	6	4	2	0	- 2	- 4	- 6
	15	5	- 1	- 3	- 1	5	15
ф ( 6 ) =	20	0	- 4	0	4	0	- 20

- 5   - 1

3    - 1   - 5

- 4  2

0   - 2

- 6

- 11 - 11 - 1

Table 3. Krawtchouk matrices

								1	1	1	1
				"1	1	1"
ф ( 0 ) = [ 1 ]   ф( 1 ) =	"1	1"	ф( 2 ) =	2	0	- 2	ф( 3 ) =	3	1	- 1	- 3
	1	- 1						3	- 1	- 1	3
				1	- 1	1
								1	- 1	1	- 1

Basic properties of Krawtchouk matrices

1)	The square of a Krawtchouk matrix is proportional to the identity matrix. ( ф( N ) ) 2 = 2 N I . This remarkable property allows one to define a Fourier-like Krawtchouk transform on integer vectors.

2)	The top row is all 1’s. The bottom row has ± 1 ’s with alternating signs, starting with + 1 . The leftmost entries are just binomial coefficients, Ф( N ) = j N ) . The rightmost entries are binomial coefficients with alternating signs, Ф ( N ) = ( - 1 ) i j N ) .
3)	There is a four-fold symmetry: Ф N ) = Ф^ = Ф ( N - j = ® NNN - j •

Krawtchouk matrices generalize Pascal’s triangle in the following sense: Visualize a stack of Kraw-tchouk matrices. The order N increasing downwards. Pascal’s triangle is formed by the leftmost columns. It turns out that Pascal’s identity holds for the other columns as well. Less obvious is another identity – call it dual Pascal.

Proposition. Set a = Ф ⁽ N ) , b = Ф ⁽ 5 ) , A = Ф^ ^{+ 1 )} , B = Ф^ + 1 ) .

The square identity is useful in producing the entries of a Krawtchouk matrix: fill the top row with 1’s, the right-most column with sign-alternating binomial coefficients. Then, apply the square identity to reproduce the matrix.

In summary, the identities considered above can be written as follows:

Cross identities:
(i)	ф( N ) +ф( N ) =ф( N + 1) i - 1 j         ij             ij	(ii)	фj N ) +ф( N ) =2Ф( N -1) jj             jj + 1              ij
(iii)	ф j N )_ф( n ^фС N + 1) jj           г - 1 j        j + 1	(iv)	Фj N ) _ф( N 1 = 2Ф( N - 1). ^ij         + 1    ^^j - 1 j  .
Square identity:

ф⁽ N ) =ф⁽ n ). +ф ( n ) +ф ( n ) . ij            i - 1 j         i - 1 j + 1         ij + 1

If each column of the matrix is multiplied by the corresponding binomial coefficient, the matrix becomes symmetric. Let B ⁽ N ) denote the ( N + 1 ) x ( N + 1 ) diagonal matrix with binomial coefficients

B(N) = ii

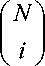
as its non-zero entries. Then, for each N <  0 , one defines the symmetric Krawtchouk matrix as

Examples: For N = 3 , we have

5 ( ^N ) = ф ( ^N ) B ^{( N} )

	"1	1	1	1 "		" 1	0	0	0"		" 1	3	3	1
5 ( 3 ) =	3	1	- 1	- 3		0	3	0	0	=	3	3	- 3	- 3
	3	- 1	- 1	3		0	0	3	0		3	- 3	- 3	3
	. 1	- 1	1	- 1		. 0	0	0	1 _		. 1	- 3	3	- 1

Some symmetric Krawtchouk matrices are displayed in Table 4.

Table 4. Symmetric Krawtchouk matrices

5 ( 0 ) = [ 1 ]		5 « =	"1 1	1 " - 1	5 ( 2 ) =		"1 2 1	2 0 - 2		1 " - 2 1	5 ( 3 ) =		"13  3 3   3    - 3 3   - 3   - 3		1 " - 3 3 - 1
													. 1     -	33
									' 1	5		10	10	5	1
	"1	4	6	4	1 "
									5	15		10	- 10	- 15	- 5
	4	8	0	- 8	- 4
5 1									10	10		- 20	- 20	10	10
	6	0   -	12	0	6	5 ( 5 )		=
									10	- 10		- 20	20	10	- 10
	4	- 8	0	8	- 4				5	- 1	5	10	10	- 15	5
	. 1	- 4	6	- 4	1 _
									. 1	-	5	10	- 10	5	- 1
				" 1	6	15		20		15		6	1  "
				6	24	30		0		- 30		- 24	- 6
				15	30	- 1	5	-	60	- 1		30	15
		5 ( 6 )	=	20	0	- 60			0	60		0	- 20
				15	- 30	- 15		60		- 15		- 30	15
				6	- 24	3	)		0	- 3	)	24	- 6
				1	- 6	15		- 20		15		- 6	1

Krawtchouk matrices from Hadamard matrices

We show the connection between the Krawtchouk matrices (and hence, polynomials) and the Sylvester-Hadamard matrices. Then we derive the Krawtchouk matrices from the classical symmetric Bernoulli ran- dom walk. This approach is continued to the quantum probability context, leading to the construction of Krawtchouk matrices via tensor powers of the elementary Krawtchouk/Hadamard matrix.

Krawtchouk’s polynomials were introduced by him in (see also). Since then, they have been found to be important in many areas of mathematics arid applications. They arise in several ways in coding theory and combinatorics, for example, in Mac Williams’ theorem on weight enumerators, and in association schemes.

In this paper, we make explicit connections between Hadamard matrices, specifically the Sylvester-Hadamard matrices, and Krawtchouk matrices. Yarlagadda and Hershey provide an overview of the subject of Sylvester-Hadamard matrices, indicating many interesting applications in. For statisticians, they point out that in Yates’ factorial analysis, the Hadamard transform provides a useful nonparametric test for association.

We review definitions and basic properties of Krawtchouk matrices. An algorithmic approach shows how to derive Krawtchouk and symmetric Krawtchouk matrices using the elementary Hadamard matrix

H =

- 1

and the Sylvester-Hadamard matrices. We presents the classical probability interpretation which leads to the quantum random walk, “quantum computer”, approach. Some remarks on calculating expectation values conclude the study. Two appendices – on tensor products and symmetric tensor spaces – are included to aid the reader as well as to establish notations.

What are Krawtchouk Matrices

One may view Krawtchouk matrices as an extension of the binomial coefficients. Consider the “degree-two algebraic rules” and translate them into a “second-degree Krawtchouk matrix”:

(a + b )2 = a2 + 2 ab + b2

(a + b)(a - b ) = a2 - b2           ^ Ф(2) = 2  0

(a - b )2 = a2 - 2ab + b2                     _1  -11

(the expansion coefficients make up the columns of the matrix). Thus the general definition:

Definition. The N th -degree Krawtchouk matrix Ф ⁽ N ) is an ( N + 1 ) x ( N + 1 ) matrix, the entries of which are determined by:

N

( 1 + u ) N ^- ' ( 1 - u ) j   £ _: Ф^ -                                   (9)

j = 0

The left-hand-side G ( u ) = ( 1 + u ) N j ( 1 - и ) j is thus the generating function for the row entries of the j^th column of Ф ⁽ N ) . Expanding gives an explicit expression:

^ j ' = £ ( - 1 ) ‘

k

( j )Г N - j ) V k Л i - k V

Krawtchouk matrices of order zero and one are:

Ф ^{( 0 )} = [ 1 ]

Ф ^{( 1 )} =

- 1

The columns of the Krawtchouk matrices contain the generalized binomials, while the rows define Krawtchouk polynomials: for order N , define the i -th Krawtchouk polynomial as the function that takes its corresponding values from the i -th row.

P N ) ( j ) = ФГ '

One can easily show that P ( j ) is indeed a degree i polynomial in j .

The basic properties of Krawtchouk matrices are:

(1) The square of a Krawtchouk matrix is proportional to the identity matrix.

( Ф ^{( N} ) ) 2 = 2 ^N • I

This remarkable property allows one to defines a Fourier-like transformation for integer vectors.

(2) The leftmost entries arc just binomial coefficients,

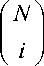
. The rightmost entries are binomial

coefficients with alternating signs, Ф ( N ) = ( - 1 ) i

" N ^

V i V

. The top row is all 1’s. The bottom row has ±l’s with

alternating signs, starting with +1.

• (3)    There is a four-fold symmetry: Ф_y ^N )| = Ф^N ) I = Ф ⁽ N ) I = Ф (, N)_iN_ I . j   jj    j

See Table 3 for Ф ^{( N} ) , 0 <  N <  6 .

If each column of the matrix is multiplied by the corresponding binomial coefficient, the matrix becomes symmetric. Let B ^{( N} ) denote the ( N + 1 ) x ( N + 1 ) diagonal matrix with binomial coefficients

<'=

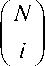
as its non-zero entries. Then, for each N >  0 , one defines the symmetric Krawtchouk matrix as

Example: For N = 3, we have

S ^{( N} ) = ф ^{( N} ) B ^{( N} )

	"1	1	1	1"	" 1	0	0	0"		" 1	3	3	1
S (3) =	3	1	- 1	- 3	0	3	0	0	=	3	3	- 3	- 3
	3	- 1	- 1	3	0	0	3	0		3	- 3	- 3	3
	1	- 1	1	- 1	0	0	0	1 J		1	- 3	3	- 1

Some symmetric Krawtchouk matrices are displayed in Table 4.

Krawtchouk tower and identities

We can say that Krawtchouk matrices generalize Pascal’s triangle. Visualize a “Pascal-Krawtchouk tower” by stacking the matrices as layers one by one, the degree N increasing downwards. Thus, Pascal’s triangle forms one side of the Pascal-Krawtchouk tower.

As might be expected, Pascal’s identity, valid for the leftmost columns, holds for the other columns as well. Less obvious is another identity – call it dual Pascal.

Lemma Let a = ф ^{( N} ) , b = Ф ^{( N} ) and A = Ф ^{( N + 1 )} , B = Ф ^{( N} + ¹ ) . Then a + b = A, b - a = B with corresponding inverse relations A + B = 2 b, A - B = 2 a .

Proof:   For a + b , consider

( 1 + u ) N - j + 1 ( 1 - u ) j = ( 1 + u ) x ( 1 + u ) N - j ( 1 - u ) J

For b - a , consider

( 1 + u ) N - j ( 1 - u ) J + 1 = ( 1 - u ) x ( 1 + u ) N - j ( 1 - u ) J

The inverse relations are immediate.

Corollary (Square identity) In a square of any four adjacent entries in a Krawtchouk matrix, the entry in the left-bottom corner is the sum of the other three, i.e.,

ac for Ф = ... b d ...

one has b = a + c + d

Proof: ( a + b ) + ( c + d ) = A + B = 2 b , hence a + c + d = b

The square identity is useful in producing the entries of a Krawtchouk matrix: fill the top row with 1’s, the right-most column with the binomial coefficients.

Then, apply the square identity to reproduce the matrix.

In summary, the identities considered above can be written as follows:

Cross identities:

( i)    ф( N )+ф( N ) =ф( N + 1) \ )        i - 1 j       ij         ij	(и)    ф <; ' + Фу- + 1 = 2 ^' n - 1 )
(iii)    < N( N )-Ф( N )=Ф( N + 1) V    )         ij         i - 1 j        ij + 1	( i u )    Ф' N )+ Ф' N 1 = 2 Ф Е;11

Square identity:

Ф⁽ N ) = ф⁽ N иф^ N ). , =ф⁽ N + 1 ) ij            i - 1 J        i - 1 j + 1          ij + 1

Krawtchouk matrices from Hadamard matrices

The identities allow us to define Krawtchouk matrices recursively, by using tensor products. One can “blow up” the symmetric Krawtchouk matrix S ⁽ n ) by taking the Kronecker product with the elementary matrix

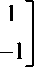
and then contracting appropriately to yield S ⁽ n ) .

Definition Define the square contraction r ( M ) of an n x n matrix M as the matrix with entries

( ГМ ) „ = Z   ^M-.                              (13)

a = 2 i - 2,2 i - 1 b = 2 j - 2,2 j - 1

where the values M_ab outside of the range ( 1,... , n ) are taken as zero.

Theorem Symmetric Krawtchouk matrices satisfy:

S(N+1) = r ( S(N)® H)

Corollery Krawtchouk matrices satisfy:

Ф ⁽ N ^{+ 1 )} = r ( ф ^{( N} ) B ⁽ N ) ® H )( B ⁽ N ⁾ ) " 1

where B is the diagonal binomial matrix defined in (13).
Example . Start with symmetric Krawtchouk matrix of order 2:
	"12  1 "
	S ( 2 ) = 2   0    - 2
	1   - 2   1
Take the tensor product with H :
	" 112 2 11 "
	1   - 12   - 2  1   - 1
	m       2  2   0   0   - 2   - 2
	S ( 2 ) ® H =
	2   - 2  0   0   - 2  2
	11   - 2 - 2  1   1
	_ 1    - 1   - 2   2    1    - 1 _
surround with zeros and contract:
	" 0   0    ;    0    0    •    0    0    ;    0    0"
	01:12:21:10
	01   ;    - 1   2   :    - 2   1   ;    - 1  0   r              n
	.             .             .              13   3   1
	0   2:2    0:0    - 2   :    - 2   0
	3   3    - 3   - 3
r S ( 2 ) ® H = r	=
V             /	.           .           .            33   - 3   - 3
	0   2    :    - 2   0    :    0    - 2   :    2   0
	.            .            .             1   - 33   - 1
	0    1:1     - 2    :     - 2    1     :     1    0     L                    J
	0    1    ;     - 1    - 2    :    2    1     ;     - 1   0
	_ 0   0    ■    0    0    :    0    0    ■    0    0 _

These features that Krawtchouk matrices can be obtained from the tensor power of the elementary matrix H . Such powers define the family of Sylvester-Hadamard matrices , (see e.g.).

Notation: Denote the Sylvester-Hadamard matrices, tensor (Kronecker) powers of the fundamental matrix H , by

H ⁽ N ) = H ® H ®„.® H                         (14)

Ntimes

The problem is that the tensor products disperse the columns and rows that have to be summed up to do the contraction. We need to identify the appropriate sets of indices.

Definition Define the binary shuffling function as the function w :N ^ N giving the “binary weight” of an integer. That is, let n = Z ^2 2k be the binary expansion of the number n . Then w (n ) = Z kdk , the number of ones in the representation.

Notice that, as sets,

w ({ 0,1,...,2 N - 1 }) = { 0,1,..., N }

Here are the first 16 values of w listed for the integers running from 0 through 2 4 - 1 = 15 :

Observe that the shuffling function can be defined recursively, setting w(0) = 0 and for 0 < k < 2N. One can thus create the sequence of values of the shuffling function by starting with 0 and then appending to the current string of values a copy of itself with values increased by 1:

0 ^ 01 ^ 0112 ^ 01121223 ^ etc.                      (15)

Now we can state the result;

Theorem Symmetric Krawtchouk matrices are reductions of Hadamard matrices as follows:

S j ' = Z H aN '

a e w ¹ ( i )

b e w ^{- 1} ( j )

Example: Let us see the Transformation for H ^{( 4} ' ^ S ^{( 4} ' . First, for typographical reasons, let use • for

• 1    and for -1. Thus,

  •

  •

  •

  •

  •

  •

  •

  •

  •

  о

  •

  о

  •

  о

  •

  •

  •

  •

  •

  •

  •

  О

  о

  •

  •

  О

  О

  H ( 1 ) =

  •

  •

  H ( 2 ) =

  •

  О

  •

  H (3) =

  •

  О

  О

  •

  •

  О

  О

  •

  •

  °

  •

  •

  о

  •

  •

  •

  •

  о

  о

  о

  °

  •

  о

  о

  •

  •

  О

  •

  о

  о

  •

  О

  •

  •

  •

  о

  о

  о

  о

  •

  •

  •

  о

  о

  •

  о

  •

  •

  °

etc. Now, applying the binary shuffling function to H ⁽⁴' , mark the rows and columns accordingly:

0 (•  •  •

1   •

1   •

2 •

1   •

2 •

The contraction is performed by summing columns with the same index, then summing rows in similar fashion. One checks from the given matrix that indeed this procedure gives the symmetric Krawtchouk ( ⁴ ) matrix S .

Below we will present the algebraic structures behind these properties.

Krawtchouk matrices and classical random walk

In this section we will give a probabilistic meaning to the Krawtchouk matrices and some of their properties.

Let ^ be independent symmetric Bernoulli random variables taking values ± 1 . Let X_N = ^ *-----* ^

be the associated random walk starting from 0. Now observe that the generating function of the elementary symmetric functions in the ^ is a martingale, in fact a discrete exponential martingale:

N

MN = П(1 * U^i) = ^Ukak (51,-“,^N ) i=1                      k where a denotes the kth elementary symmetric function. The martingale property is immediate since each ^ has mean 0. Suppose that at time N , the number of the ^ that are equal to - 1 is jN, with the rest equal to +1. Then jN = (N - XN ) /2 and MN can be expressed solely in terms of N and X , or, equivalently, of N and j

M. = ( 1 * u ) N -- (1 - и ) - = ( 1 * u f * X^{- ) /2} ( 1 - u ) ⁽ N - X N ^{) /2}

From the generating function for the Krawtchouk matrices, follows

M„ =      ( N >

N                i , j_N

i so that as functions on the Bernoulli space, each sequence of random variables Ф(N) is a martingale.

• i ,    j_N

Now we can interpret two basic recurrences of section 2. For a fixed column of Ф ( N ) to get the corresponding column in Ф ⁽ N ^{+ 1 )} one uses the Pascal’s triangle recurrence:

Ф ( N ) ₊ ф⁽ N ) = ф⁽ N ^{+ 1 )} i ^{- 1} j       ij         ij

This follows in the probabilistic setting by writing M _{x +1} = (1 + u^ ) M _x and remarking that for j to remain constant, ^ must take the value +1, with consequences as in the purely algebraic context. The martingale property is more interesting in the present context. We have

Ф(N) = E ( Ф(N) 1г,..., ^ ) =1 ( Ф(N+1) + Ф(N+1) I iJN        у 1Jn+1 1^1’    N^N J ^ \ ijN+1       iJN / since half the time ^+x is -1, increasing j by 1, and half the time jN is unchanged. Thus, writing j for jN ,

_Ф< ^N ) = ¹ ( _Ф ^{( N + 1 )} _{+ Ф} ^{( N + 1 )} i^j       2 у i^j N + 1          i jn /

The interpretation of Krawtchouk polynomials as elementary symmetric functions on the Bernoulli space allows one to derive their analytic properties using probabilistic methods with corresponding interpretations.