Some Properties of Anti Imprecise Subgroup and its Application

The notion of classical sets is generalized in the theory of FSs. It was in 1965 that Zadeh [1] first proposed this notion. Zadeh [1] began the study of FS and since then this particular branch of mathematics has been brilliantly focused for its diverse applications. Numerous authors have extended this theory to a broad spectrum of mathematics and combined it with different uncertainty approaches. Rosenfeld [ 2] initiated the study of algebraic structures on FSs by defining FGs. This FG theory is one of the most impressive uses of Zadeh's FS theory. The idea of an FS G was first proposed by Rosenfeld [ 2] in 1971 using the idea of Zadeh's FS b of a set. Rosenfeld's research [ 2] served as an inspiration for fuzzy abstract algebra's creation. Das [23], Mukherjee and Bhattacharya [19,20,21,22] have all conducted additional research on this topic. Biswas [3] introduced the concept of anti FS G which is nothing but the complement of Rosenfeld's [2] FS_G theory, constructed using Zadeh's complement definition of FS and established some fundamental properties of this phenomenon. Onasanya [4] established many important anti fuzzy properties of FGs. However, the claim that FS theory is an extension of traditional set theory is refuted by Zadeh's [1] formulation of FS complement, which does not adhere to the two universal laws of the traditional set theory. Regarding this, Baruah [6] came to the conclusion that the fuzzy complement definition had a flaw because the two functions—fuzzy MF and fuzzy RF—were regarded as one and the same in the previous definition of FS. This ultimately led to the conclusion that Zadeh's concept of the fuzzy complement set does not adhere to the two key principles of traditional set theory: intersection of a FS and its complement is null set; and union of a FS and its complement is a universal set. In 1999, H. K Baruah [5,6,7,8] redefined the definition of the complement of a FS to overcome such shortcomings in the existing definition of a FS. We were then able to obtain a new definition of the fuzzy complement of an FS after Baruah [5,6,7,8] provided a new definition of FSs in terms of MF and RF. Additionally, this expanded definition of FS can get around the problem with

Zadeh's [1] FS and provide us with the intersection of an FS and its complement as null set; and the union of a FS and its complement as a universal set. This expanded definition of an FS with a new complement form is called an IS. Numerous authors have written about this IS, which satisfies many of the traditional set theoretical features. Later, the theory is used in numerous fuzzy number extension investigations. This new definition has been addressed by many other authors, which can be viewed in [9,10,11,12,13,14,15,16,17]. In 2024, Narzary and Borgoyary [18], used the definition of an IS to study the algebraic structure of FG and FS G in terms of MF and RF to construct an extended version called IG, which is basically an extension of a FG theory. As the extended concept of IS is more convenient than the existing FS so, the properties and results satisfied by IG is more convenient and satisfactory than existing FG theory. In the same year, Narzary [18] used the concept of IGs to develop many other fundamental characterization of the IS G .

The main objective of this paper is to introduce anti IG and therefore anti IS_G which have been established to study some fundamental properties of traditional group theory with respect to anti IS_G. This study of anti IG is important as it is based on Baruah's [7] extension of existing FS definition which can overcome the shortcomings of Zadeh's FS definition. Here, the concept of anti IG is basically the complement of IG which is defined in terms of MF and RF based on the complement definition of IS by Baruah [7]. This paper is a continuation of the idea of IG and IS G s defined in [18] using the concept of IS by Baruah [7]. We also used this anti IS G to construct a network structure, which shows that every anti IS G is a closed network structure. And, this structure can be used to solve some networking problems. The properties of anti imprecise groups enable the creation of a wide range of fascinating network diagrams that could have practical uses in the domains of invention and research.

For our entire study ‘G’ is considered as the precise group and ‘X’ as the universal set.

2.    Preliminaries 2.1.    Definition ([2])

A FS b U y is said of to be a FS G of G if

• (i)    исш^иаолиа , ); v t^eG

• (ii)    иД - ^г) >u_f(U v t i e G

• (iii)    U_f(e) > u_f(t J; V t _i e G

• 2.2.    Definition ([7])

• 2.3.    Definition ([24])

• 2.4.    Definition ([7])

• 2.5.    Definition ([7])

• 2.6.    Definition [12]

If u „ (t , ) is a fuzzy MF and u²(t_i) is a fuzzy RF such that 0 < u^;Ct J < u ^ Ct i ) < 1, then the IS is defined as A j = {t_i,u ™ Ct_i),u²Ct_i);t_i e X} where X is the universal set and u J CX) = u ^ CX) — u^X) gives the actual membership value for all t _i e X. For convenient of writing above imprecise set is denoted by (u ^ , u²)(t _i ); t _i e X.

If A j = {t , , u ^ Ct_i),u 2 (t _i);t_i e X} and B= = {t _i, u ^ Ct ^u ^ Ct_i );t _i e X} are two IS over the universe X then A C Bi iff u ^ Ct i ) c u ^ CX) and u ^ Ct i ) c u ^ Ct i ).

If Cu Jn ,u²) is an IS_b of X , then the complement of Cu^u²) denoted by Cu^u²^, is the IS of X given by Cu ^ , u²)^cCt_i) = {t_i, 1, u ^ CX); t_i e X} where 1 — u ^ is the non MV of t_i in X .

If  A^  and Bi^c are the complements of the two ISs A j = {t^u ^ CX), u^XXX e X} and

Bi = {t _п u^Ct 0, u^Ct 0; t _i e X} respectively then their union and intersection are respectively, A i ^c UBA = ^{t_v 1^0 и^Д^О = {t^max^lbmi^u^t i Xu^A));t i e X}

A i ^c nB^ = ^{t i , Xu^t iB П {^t^^t i )} = {tnminaJLmax^urXt i Xu^t i )) ; t i e X}

Let an IS b Cu ^ ,u^;) of G together with a binary composition ‘*’ be called an IG [Cu ^ ,u^;),*], if (i) Cu ™ , u^;)( t_it₂ ) > Cu ™ , u²)Ct_i) Л Cu ^ , u^;)Ct₂ ); t_i, t₂ e G, where ' Л ' is the minimum operator (ii) Cu ™ ,u²)(t i ^{- i}) > Cu ^ ,^)^); V t i e G

• (iii)    Cu™,u2)C e) > Cu™,u2)Ct i); V t i e G

• 2.7.    Definition

3.    Anti ISG

• 3.1.    Definition

A Cayley table is a technique for describing an algebraic structure (usually a finite group) by putting all the elements in a square array to show the binary operation of the elements in a group. In our study, Cayley table is used to present binary operations of the elements of a precise group.

The concept of complement definition of IS by Baruah [7] has been applied in the Definition 2.6 of IS G by Narzary and Borgoyary [18] to establish the concept of anti IG and therefore of anti IS G to study some fundamental properties with respect to anti IS G . So, the concept of anti IS G is basically the complement of IS G which is defined in terms of MF and RF based on the complement definition of IS by Baruah [7].

Let G be a group. A FS_b (u j„ , u ^ )^c of G is called anti IS G of G if for t ₁ , t ₂ EG (i) (u ^ ,^/ (t 1 ,t 2 ) <  m azRu^u²/ (t J, (u ^ ,^/ (t 2 )}; V ;t U 2 e G where m^Ku^u²^ (tj, (u^u^ (t 2 )} = (u^u^ V (u^u²)^) = (u^^) V u^ ),u²(^ ) Л u^)) and ' V' is the maximum operator.

• (ii)    (u^/ (tr ^ < (uL^HU V t1 e G

4.    Some Properties of Anti ISG 4.1.    Property

• 4.1.1    Example

If A ; and Bi are anti IS G then the complement of the union of A1 and Bi is not an anti IS G i.e; (A_i U B_i)^c is not an anti IS G .

Proof:

To prove this statement Example 4.1.1 is cited.

Let G = {1, -1, i, —i} be a group under multiplication.

Table 1. Cayley table for G = {1, —1, i, —i}

* 1 -1 i -i 1 1 -1 i -i -1 -1 1 -i i i i -i -1 1 -i -i i 1 -1 where 1 is the identity element, i2 = —1, (—i)2 = —1, (i)(—i) = 1

Let fU1 U2        (1,0);  ^ = 1,—1QX

(um,ur)(      {(0.92,0.08); t1 = i,—i

W.uMi) = [<0,0)0^ ^L—1—

Equation (1) and (2) are clearly ISGs by Definition 2.6

Ai = (um,u2)C(t1 ) = {(1Д92);1 t1 = i,—i

D _ Л.З ..4X C[j X _ [ ^{(1,1); i}/ ^t 1 = 1,^—1/ДХ

Bl   (um,ur) (to   {(1,0.9);i/ t1 = i,—i

Again, by Definition 2.4 and 3.1, equation (3) and equation (4) are respective anti IS G s of A i and Bi.

Now, the union of equation (3) and equation (4) is given by

Ai U B_t

((1,1); i/ t 1 = 1,—1 ^{(1,0.9);i/ t 1 = i,—i

which is nothing but equal to Bi and so equation (5) is an anti IS G .

Then the complement of equation (5) is given by

Ai UB^

( (1,0);if t i = 1,-1

^{(0.9,0.1);if t_i = i,-i

which is nothing but equation (2), so equation (6) is an ISG not an anti ISG.

• 4.2.    Property

• 4.2.1    Example

If A i and B i are anti IS G such that Q4f U B ? ) C C^c then C^c is an anti IS G .

Proof:

To prove this statement Example 4.2.1 is cited.

From previous Example 4.1.1 let, c ((1,1); t! = 1,-1

1   {(1,0.92); ti = i,—i

B f = {

(1,1);  t i = 1,—1

(1,0.9);  ti = i,—i

Let us consider another IS b , C on G = {1, -1, i, — i} by

((0.9,0);  t i = 1

C = (4,ur6)(ti) =  (0.4,0.4); ti = —1

{(0.3,0.3); ti = i,—i then by Definition 2.4, anti imprecise subsets of equation (9) is,

(1,0.9); t i = 1

Cc = (u^,ur6)c(ti) =  (1,0.4); ti = —1

{(1,0.3); ti = i,—i such that лc.^c-g1,1);  ti = i,—i , rnn

Ai UBi   {(1,0.9); ti = i,—i“C

Thus, by Definition 2.3, A c U Bf C C^c.

And, equation (11) and by Definition 2.4 and 3.1, implies that C^c must be an anti IS G .

• 4.3.    Property

• 4.3.1    Example

If A c and Bi are anti IS G s such that (^ c U B))^c C C then C must be an IS G .

Proof:

To prove this statement Example 4.3.1 is cited.

From previous Example 4.1.1, let c   ((U);  ti = l,—l

^Al   {(1,0.92); t_i = i,—i                                           ^{(  )}

c ((1,1); t i = 1,—1 ¹    {(1,0.9);   t_i = i,—i                                               ^{(  )}

Then equation (12) and (13) are two anti IS G s on G = {1, —1, i, —i} by Definition 2.4 and 3.1

And, let

( (1,0);  t i = 1,—1

{(0.93,0.05);  ti = i,—i be an ISb on G = {1, —1, i, —i}

Then, the complement of the union of equation (12) and (13) by Definition 2.4, 2.5 and equation (2) is

PUI)   = 1,-1

(AUBJ   ^{(0.9,0.1);  ^ = 1,-1                                ⁽¹⁵⁾

which is clearly an IS G by Definition 2.6 such that (Ac U B f )^c ^ C by Definition 2.3 then C must be an IS G by Definition 2.6.

• 4.4.    Proposition

Union of two anti ISGs is again an anti ISG.

Proof:

Let (u ^ , U j )^c and (u ^ , u ^ )^c be an anti IS G s of G Then

^((u n ^,u r ^{2)c U} (Ц^т^НМ г ) = m^ax^[(u m ^,u2)c(t 1 ^t 2 ^), (^XH^)]

< max{rnax{(u m ,u²)^c(t₁), (u m ,m_r²)^c(t₂)},rnax{(u m ,m_r⁴)^c(t₁), (u^n⁴)^)}}

= m^a4m^ax{^(u m ^,u2)c(t 1 ^), О^п^ГО^}, m^avЦ¹u^,u2)^c(t 2 )^, (e, ш Г )^c(U)}}

= m^ax{C^(u 4n , ^u ? ^{)c U (}4^,m 4 ^))c(t 1 )^,((4^u r ²)^{c U} OCjn r' )ПЫ}

Thus, ^((u n ^{,u2)c U} fen^H^) < rnax{^((u m ^{,u2)c U (}4^,m 4 ^))c(t 1 )^,((4^u r ²)^{c U (u} n ^,m4))c(t 2 ^)}

Also, ((u m ,u_r²)^c U (u^m^Ht i ^-1) = maxKum^Ht i ^-1),^²,,™⁴)/^^-1)}

= rnax{(u m , u 4 )^c(t₁), (u n ,m⁴)^c(t₁)} by Definition 3.1 ^(u^rU^XWO

Hence, ((u ^ , u²)^c U (u ^ , m⁴))^c is an anti IS G of G.

• 4.5.    Corollary

• 4.6.    Proposition

Union of a family of anti ISGs of a group is again an anti ISG of the group.

Intersection of any two anti ISGs is not necessarily an anti ISG.

Proof:

Let us consider two anti ISGs

(u1 u2 )c - [(1,0.9);  t1-e,cQ0

(um,ur)    {(1,0.5);  t1 = a,b and

(uз^-Р'0-8); ^ = e,a

(um,ur)    {(1,0.7); t ^b ,c over the multiplicative group f4 = { e, a, b, c} and Cayley table for f4 is given in Table 2; where e is the identity element, a2 = b2 = c2 = e , ab = c, ac = b , b c = a

Table 2. Cayley table for K4
	*	e	a	b	c
	e	e	a	b	c
	a	a	e	c	b
	b	b	c	e	a
	c	c	b	a	e

Then, the intersection of equation (16) and (17) by Definition 2.5 is

(1,0.9);  t 1 =e ,c

(u^u ? )^cn(u m ,u 4 )^c=  (1,0.8);  t 1 =a                              (18)

(1,0.7);  t 1 =b

But,

[(u^u ? )^c П (елГГЦ c a) = (1,0.7)

£ (1,0.8)

= mra{[(u { ,u_r²)^c n (u^X/Kc), [(i4,u_r²)^c n (u^X/Ka)}

So, (u j„ ,u 4 )^c n (u ^, ,u⁴)^c is not an anti IS G by Definition 3.1.

5.    Application of an Anti IG in Networking Problem

There are several applications of group theory in various areas of mathematics. In geometry, groups are used to express concepts like symmetry and specific kinds of transformations. For instance, in symmetricity of molecules, one symmetric figure A is transformed to another symmetric figure B. But in between this transformation from A to B there are a number of imprecise transformed figures of A to B. Here, the concept of an imprecise subgroup is used to present the journey of these imprecise transformed figures during the interval in between two precise symmetric figures A and B. And, the overall set of precise symmetric figures and imprecise symmetric transformed figures represents the concept of an imprecise subgroup with respect to the operation of composition. And, the overall set of complement of such imprecise transformed figures are used to explain the concept of anti IS_G with respect to the operation of composition. This anti IS_G then represents a closed network figure which can be applicable in various networking problem. Here, a highly symmetric molecule C H₄ is studied by the use of anti I S_G . The elements in 2 ₄ = CH₄ are the transformed figures of C H ₄ due to different compositions, given by 2 ₄ = {r ° ,r^{9 0} , r^{1 8} ° ,r^{2 7 0} , D1,01, D , D / } where r ° is rotation of 0 ° , r⁹⁰ is rotation of 90 ° , r^{1 8} ° is rotation of 180 ° , r^{2 7} ° is rotation of 270 ° , 1)1 is flip about a horizontal axis, 0 1 is flip about a vertical axis, D is flip about the main diagonal and D / is flip about the other diagonal. The Cayley table of 2₄ is given in Table 3.

Table 3. Cayley Table of 2 4

*	r°	r90	r180	r270	D1	01	$	D 7
r°	r°	r90	r180	r270	D1	01	$	D /
r90	r90	r180	r270	r°	$	D /	01	D1
r180	r180	r270	r°	r90	01	D1	D /	$
r270	r270	r°	r90	r180	D /	$	D1	01
D1	D1	D /	01	$	r°	r180	r270	r90
01	01	$	D1	D /	r180	r°	r90	r270
$	$	D1	D /	01	r90	r270	r°	r180
D /	D /	01	$	D1	r270	r90	r180	r°

Then the grades of MF and RF are assigned to each of the elements of 24 given in equation (19)

f(0.9,0.1); if ^ =r ° ,r⁹⁰,r¹⁸⁰,r²⁷⁰ {(0.75,0.2); if t ₁ = D1,01,D ,D /

which is clearly an ISG. Now,

(4,1 2 nt^R⁹);

' r     17    ((1,0.75)

f  t 1 =r° ,r9 °,r 1 8 ° ,r 2 7 ° if t 1=D1,01,D ,D / is an anti ISG of equation (19).

Now, we can construct a network figure by using the elements of the precise group as nodes of the network figure and the imprecise value of the same elements as the imprecise path between two elements indicated by the connecting lines.

These connecting lines are given by

(4,1 2 )(r⁹ ° D1) = (4,1 2 X®) = (0.75,0.2);

(4,1 2 )(r⁹ ° 01) = (4,1 2 )(D / ) = (0.75,0.2);

(4,1 2 )(r⁹ ° D ) = (14 u² )(01) = (0.75,0.2);

(4,1 2 )(r ⁹ ° D / ) = (4,1 2 )(D1) = (0.75,0.2);

(4,1 2 )(r¹⁸⁰I)1) = (4,1 2 )(01) = (0.75,0.2);

(4,1 2 )4 ⁸ ° 01) = (4,1 2 )(D1) = (0.75,0.2);

(4,1 2 Xr^{1 8} ° D ) = (4,1 2 )(D / ) = (0.75,0.2);

(4,1 2 )(r¹⁸⁰D / ) = (4,1 2 X®) = (0.75,0.2);

⁽4,1 2 ⁾⁽r^{2 7} ° D1) = ⁽4,1 2 )(D / ) = (0.75,0.2);

(4,1 2 )(r^{2 7} ° 01) = (4,1 2 )(®) = (0.75,0.2);

(4,1 2 )(r^{2 70}D) = (4,1 2 )(D1) = (0.75,0.2);

⁽4,1 2 ⁾(r²⁷⁰D^/) = ⁽4,1 2 ⁾⁽01) = ⁽0.75,0.2);

444 )(r^{9 0} г⁹ ° ) = (14,4 Xr^{1 8} ° ) = (0.9,0.1);

(14,4 )(г⁹ ° г¹⁸ ° ) = (144)4^{2 7} ° ) = (0.9,0.1);

444 )(г⁹ ° г^{2 7} ° ) = (144 )(I ° ) = (0.9,0.1);

444 )(г¹⁸ ° 270) = 444)4⁹ ° ) = (0.9,0.1);

444 )(Г^{2 7} ° 270) = 444)4¹⁸ ° ) = (0.9,0.1);

444)($Ц1) = 444)(r ° ) = (0.9,0.1);

(144 )4Ы) = 444 )(r¹⁸ ° ) = (0.9,0.1);

(144 )41® ) = (144 )4 ^{2 7} ° ) = (0.9,0.1);

444 ⁾(l)1®^/) = 444 ⁾4 ’° ⁾ = ⁽0.9,0.1);

(4,,4)4Ы) = (144 )4 ° ) = (0.9,0.1);

(144 )41®) = (144 )4⁹ ° ) = (0.9,0.1);

444 X^D1® / ) = ⁽141 r ² )4 ^{2 7} ° ) = ⁽0.9,0.1);

(144 )(®®) = (141 г ² )(r ° ) = (0.9,0.1);

⁽141 ? X®® / ) = ⁽144 ⁾⁽r¹⁸ ° ) = ⁽0.9,0.1);

(144 )(® / ® / ) = (144 )(Г ° ) = (0.9,0.1)

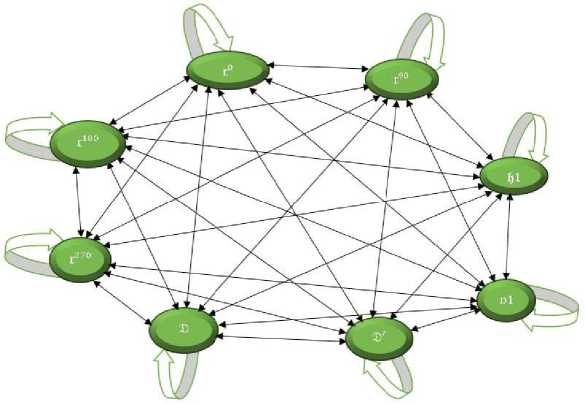
Fig. 1. Network figure of equation (20).

Since the imprecise values are commutative so each connecting lines again get connected towards the opposite node. Here, the elements of 24 represents the nodes for the model of Fig. 1 and the connecting line between two elements are the imprecise path which represents a journey of converting from one element figure to the another due to composition and resulting a closed network Fig. 1. And, the anti imprecise value of each element represents the non completion journey of one element to the another. Since each of the elements of under composition of symmetries with identity element gives out the self element so it results in creating a self loop around each element. And, the composition of symmetries between two different elements gives an imprecise path of either (0.9,0.1) or (0.75,0.2) resulting in anti imprecise path of either (1,0.9) or (1,0.75) elements. So each anti imprecise value represents a not completing journey from one node to the other. And, all these connecting lines together with the loops form an anti IG which in return can be represented in the form of a closed network figure. The number of nodes and connecting lines may differ depending upon the anti IG we are considering. Thus we can generate several network structures depending on the number of elements in the group.

6.    Conclusion

The main objective of our work is to lead algebraic properties in a more conventional way in the world of imprecision that could hold traditional set theory. Therefore, we have introduced ISG with fundamental properties in our previous work which is based on the definition of IS. In this article, we have introduced anti ISG based on the complement definition of IS and established some interesting properties with some examples. This anti ISbs from the anti ISG together with the ISG can create the closed network diagram that is discussed in the article’s final part. The features of anti ISGs allow for the discovery of a variety of intriguing network diagrams, which may find useful applications in the fields of research and innovations. There are, however, a great deal of theories and properties that need to be looked into for the study of anti IG.

Acknowledgment

The first author acknowledges the financial support received from the University Grant Commission, New Delhi under the Scheme of the National Fellowship for Higher Education (NFHE) vide award letter-number 202021-NFST-ASS-01210, Dated 20th September 2021 to carry out this research work.

List of Abbreviations

FS FS b MF RF MV FG FS G IS IS b IG IS G

Fuzzy Set Fuzzy Subset Membership Function Reference Function Membership Value Fuzzy Group Fuzzy Subgroup Imprecise Set Imprecise Subset Imprecise Group Imprecise Subgroup