Some Results on Optimal Dividend Problem in Two Risk Models

Published Online December 2010 in MECS

The optimal dividend problem pioneered in [2]. Since then, there has been a wave of research focusing on finding the dividend payment strategy for the diffusion model and the compound Poisson risk model. In the present papers, the authors provided the solutions of the optimization problems where the companies control their risk before the cash reserves hit or fall below 0 .

For the optimal dividend problem of the compound Poisson risk model perturbed by diffusion, many papers focus on integro-differential equations for the expected discounted penalty function, as well as some ruin related functional such as the probability of ultimate ruin, the time of ruin and the surplus before ruin and the deficit at ruin. In these papers, the authors considered the problems

Footnotes:

Manuscript received July 1, 2010; revised September 1, 2010;

accepted September 20, 2010.

Corresponding author: Shuaiqi Zhang within the framework that the dividend strategy is the so-called threshold dividend strategy or the barrier strategy or the multi-layer strategy. Ref.[1] studied the optimality of the dividend policy for the jump diffusion process. In this paper, some further results on the optimal dividend strategy are obtained in section III. Specifically, it turns out that there can be essentially two different solutions depending on the model's parameters. If

-("2" ^£ в + c ) + в — 0 , the initial capital should be paid out as dividend immediately, and the ruin occurs. If 1 2

- ("2 ^£ в + c ) + в <  0 , the optimal strategy is to pay everything in excess of the optimal dividend barrier, whenever the reserve reaches the barrier, and the process continues. The paper also extends the controlled model with considering the existence of the proportional transaction costs. It is shown that the amount of the dividend increases as the proportional rate 1 — k decreases. What is also interesting is that the dividend barrier in the solution of this problem is the same as the barrier without proportional costs. In other words, proportional costs factor has no effects on the dividend barrier.

As for the dividend problems with constraints, [3] considered diffusion process under the restrictions that that the dividends should not be paid out unless the surplus has reached a level b0 > b . It is shown that in this case a barrier strategy at b0 is optimal. This inspires us to think a question of main interest: can we find the optimal dividend strategy of the compound Poisson risk model with solvency constraints? Or can we find the optimal dividend strategy of the compound Poisson risk model perturbed by diffusion with solvency constraints?

This paper makes the same assumptions as in [3], but differently formulated because of the model we discuss are the compound Poisson risk model and compound Poisson risk model perturbed by diffusion. The objective is to maximize the discounted dividend payment with solvency constrains before the time of ruin. We solve the problem completely when the individual claim amounts are generally distributed, rather than exponentially distributed.

The paper is organized as follows: Section II establishes the control model. In Section III, some properties of the value function are presented. Section

IV discusses some further results to the control problem when claims are exponentially distributed. In section V, the optimal dividend problem of the compound Poisson risk model with solvency constraints is solved. In section VI, the optimal dividend problem of the compound Poisson risk model perturbed by diffusion with solvency constraints is considered.

• II.    Formulation of the Control Problems

To give a rigorous mathematical formulation of the optimization problem, we start with a filtered probability space { Q ,F,{F t } t _a o ,P} . We assume that in the absence of dividends, the compound Poisson risk model X_t ⁰ is given by

N ( t )

• x, = x + ct -У y , ti i = 1

and the compound Poisson risk model perturbed by a diffusion is given by

N ( t )

Xb = x + ct -У Y + e W , tit i = 1

where X > 0 is the initial reserve, c > 0 is the premium rate, {N(t)} is a Poisson process with intensity X > 0 and {Yi } is an i.i.d. sequence of strictly positive random variables with distribution function F(y)and probability density function f (y). The claim sizes {Yi }and the claim arrival process N(t) are assumed to be independent. We assume that EY ] = Ц<^

W; t >  0} is a standard Wiener process that is

N ( t )

independent of the aggregate claims process St = ^ Yk k=1

and e is the dispersion parameter. X^ ( X^ ) is adapted to the smallest right-continuous filtration {F _t } _t > 0 . If we want to indicate that the initial capital is x , we write P _x and E _x for the probability measure and the expectation, respectively. Otherwise, we dismiss the letter x and write P and E .

We now enrich the compound Poison risk model (the compound Poisson risk model perturbed by diffusion). We denote by {Dt1} the aggregate dividends paid between time zero and time t . {Dt1} ({Dt2}) is càglàd, increasing and adapted process with D0 = 0 (D0 = 0) .

The dynamics of the controlled compound Poisson risk model is given by

N ( t )

X ' = x + ct -У Y - D ' .

tit i=i

The policy П 1 is said to be admissible if the process { Dt ¹} is {F _t } _t > 0 -adapted, increasing and adapted process with D ₀ ¹ = 0 . The class of all admissible controls is denoted by П 1 .

The time of ruin is defined by

T ⁿ : = inf{ t >  0: Xt ¹ <  0}.

With each admissible control П 1 G П 1 , we associate a performance functional V ^п ' ( X ) defined by

T - '

V ( X ) = E x I J 0 . e d D 1 J , where ‘ is the discount rate. The objective is to find the control that maximizes the performance index. We define the value function V ¹ by

V ¹ ( x ) : = sup { V ⁿ ' ( x ); n 1 g П , } .

The optimal policy П 1 is a policy for which the following equality is true:

V ' ( x ) = V ⁿ * ( x ) .

If the company is not be allowed to pay dividends unless the surplus is more than b_c ¹ . Mathematically such restriction can be written as

Г e "I { x₅< ftdD = °-

If we impose restrictions of the form that no dividends are allowed to be paid out unless surplus is at least bc1 , and the surplus immediately after payment can not be below bc1 . In this case, we denote admissible strategy by nc. We define the performance index by nc cT

V ⁴( x ) = ^E x / 0 -

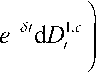
The value function is defined by

V(x ): = sup{ V ⁿ c ( x ); П Gn c } .

The optimal policy П 1 is a policy for which the following equality is true:

V j( x ) = V ⁿ c ‘( x ) .

We now enrich the compound Poisson risk model perturbed by diffusion. We denote by {Dt2} the aggregate dividends paid between time zero and time t . {Dt2} is càglàd, increasing and adapted process with D02 = 0 .

The dynamics of the controlled compound Poisson risk model perturbed by diffusion is given by

N ( t )

X 2 = x + ct-У Y + e W - D ²   .

titt i=1

The policy is said to be admissible if the process { D²} is {F _t } _t > 0 -adapted, increasing and adapted process with D 02 = 0 . The class of all admissible

controls is denoted by П 2 .

The time of ruin is defined by

T^{71 2} : = inf{ t >  0: Xt <  0}.

With each admissible control П ₂ e П ₂ , we associate

x + Erf e ^{0 t}c d t ] = x + ^— . ^x Jo                  о

This is the upper bound of any admissible strategy, i.e.,

V 1 ( x ) <  x + ^- . о

Since П ^- is a subset of П 1 , obviously,

V j( x ) <  V 1 ( x ) .

This completes the proof.

a performance functional V^{71 2} ( x ) defined by

V^{71 2}( x ) = E I I ² e'* d D ² I .

^x i Jo-              t j

The value function V ² ( x ) by

V ² ( x ) : = sup { V” ² ( x ); л ₂ e П ₂} .

The optimal policy 71 ₂ is a policy for which the following equality is true:

V ²( x ) = V ” ²( x ) .

If the company is not be allowed to pay dividends unless the surplus is more than b_c ² . Mathematically such restriction can be written as

C e "  ° I { X — <   d' = 0.

If we impose restrictions of the form that no dividends are allowed to be paid out unless surplus is at least level b_c ² , and the surplus immediately after payment can not be below b_c ² . In this case, we denote admissible

Lemma 3.2. The function V ² ( x ) is increasing with

V ² ( x ) - V ² ( y ) >  x — y for 0 <  y <  x .For any x >  0 , V ²( x ) <  x + Ц + ^— .

о

V ² ( x ) is differentiable with V ² ( x ) >  1 .

Rroof. For any £ >  0 , define a strategy 77 ₂ satisfing V” ² ( y ) >  V ² ( y ) — £ . 77 2 is a new strategy for x > y . While 77 ₂ is defined as: x — y is paid immediately as dividend and then the strategy 77 ₂ with initial capital y is followed. Therefore,

V ²( x ) >  x - y + V^{71 2}( y ) >  x — y + V ²( y ) — £ .

From the arbitrary property of £ , we have V ² ( x ) — V ² ( y ) >  x — y for 0 <  y <  x . In particular, V ² ( x ) is increasing. It is easy to see that V ² ( x ) >  1 .

strategy by П 2 . We define the performance index by c            I T T*^c             I

V ²( x ) = E x К e-^stD .

The value function is defined by

V I x ): = sup{ V ' ^c ( x ) П еП 2 }.

The optimal policy П is a policy for which the following equality is true: 2*

V - x ) = V ( x ) .

Now we prove that V ² ( x ) <  x + Ц +-- . о

The proof follows the same line as Proposition 3.1 in

[4]. Define a stochastic process Z_t by

Zt = x + ct + £Wt, and

T : = inf{ t >  0: Z_t <  0} .

We obtain

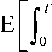
e ^-O s d Z_s

= E

f T e ^{- O s}c d s

^

III. Some Properties of the Value Function

We start with two lemmas.

Lemma 3.1. The function V ¹ ( x ) and V_c ¹ ( x ) are bounded. Moreover,

V K x ) <  V 1 ( x ) <  x + - . о

Rroof . To get the upper bound of the value function V 1 ( x ) , we consider a strategy 77 1 defined as follows: the initial capital x is paid immediately and then the dividends are paid at rate c .Then,

Г ^ e           C

< E f e ~ ^{8 s}c d s = - .

L^J о          J 0

From Itô formula,

-ST*^2 v2

e    ^X_T - 2

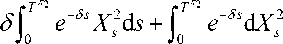
Since X²_I^ <  0 , it follows that

T ^{n 2}

Г T" ²    X 0

^— E f o   e-° -dxi

T "²

— E ° f

J 0

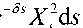
— E

-ST*"2 v e    XT- 2

< x + ^ .

Clearly, combining (1) and (2), we obtain

E Г 2 - e - ^{8 1} d D²

J 0-               t

= - ^{( s} 1 ^{+ P )}( ^s 3 ^{- s} 2 ) B

( s 3 + ^{P )( s} 1 ^- s 2 ) 3

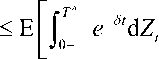
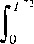
e -^{S t} d X 2

c

< x + Ц +-- .

S

This is the upper bound.

Since П 2 is a subset of П ₂ , obviously, V_c ²( x ) <  V ²( x ) .

This completes the proof.

Furthermore, we can conclude that B ₁ , B ₂ and B ₃ satisfy

B 1 B ₃ <  0, B ₂ B ₃ <  0, B 1 B ₂>0.

Now, we claim that B ₁ <  0 , B ₂ <  0 and B ₃ >0 . Because if B 1 >  0 , B ₂ >  0 , B ₃<0 , we have

V ² ' (0) = B 1 s 1 + B ₂ s ₂ + B ₃ s ₃ .

This contradicts with the fact that V ² ( x ) is increasing.

From V ² ( b ) = 1 , we have

IV. The Solution of the control problem without

RESTRICTION

The dynamic programming principle helps us to derive the Hamilton-Jacobi-Bellman (HJB) equation.

To obtain the solution, we start with the HJB equation max { 2 e² V "( x ) + cV ‘ ( x ) - ( 2 + S ) V ( x ) + 2 j ₀ x V ( x - y )d F ( y ), 1 - V* ( x ) } = 0.        (3)

For more detailed and complete account of the derivation, we readers should consult with [1].

In this section, we assume that the individual claim amounts are exponentially distributed, f (y) = Pe-Py, y > 0.

From some simple calculation, as in [1], the solution to the ordinary differential equation

2 e Х ' ( x ) + (2 e ² P + c )V"(. x )

B 1 s 1 e^b + B ₂ s ₂ e^{s 2 b} + B ₃ s ₃ e^{s 3 b} = 1.

Combining with the (6) and (7), we have

B =- ^{( s} 1 + ^{P )( s} 3 ^{- s} 2 ) { _ ^{( s} 1 + ^{P )( s} 3 ^{- s} 2 ) ses b

• ^{1     ( s} 3 ^{+ P )( s} 1 ^{- s} 2 )    ^{( s} 3 ^{+ P )( s} 1 ^{- s} 2 ) ¹

+ ^{( s 2 + P )( s 3 - s} 1 )     2 b +     3 ^b } ^{- 1} ,     (8)

( s 3 + P )( s i - s 2 ) ²

_B = ^{( s} 2 ^{+ P )}( ^s 3 ^{- s} 1 ) { - ^{( s} 1 ^{+ P )( s} 3 ^{- s} 2 ) _ses b

• ^{2   ( s} 3 ^{+ P )}( ^s 1 ^{- s} 2 )    ^{( s} 3 ^{+ P )( s} 1 ^{- s} 2 ) ¹

+ (s2 + P)(s3   s1)     2b + s e3b}-1,(9 )

(s 3 + P)( si - s 2) 2        3'

B = _{{ -} ^{( s} 1 ^{+ P )( s} 3 ^- s 2 ) „ „ s , b + ^{( s} 2 ^{+ P )(} s 3 ^{- s} 1 ) „ _p 2 2 b

^{3      (} s 3 ^{+ P )( s} 1 ^- s 2 ) ^{1       (} s 3 ^{+ P )( s} 1 ^- s 2 ) ²

+s3e 3b }-1 .(10)

From V ² ( b ) = 0 , we have

+ ( c P - 2 - S ) V ₂ ' ( x ) - SP V 2 ( x ) = 0

is given by

V ² ( x ) = B 1 e¹ + B ₂ e ^{2 x} + B ₃ e ^{3 x} ,       (4 )

-

^{( s} 1 ^{+ P )( s} 3 ^{- s} 2 )

^{( s} 3 ^{+ P )( s} 1 ^{- s} 2 ) + s ₃ ² e^s 3 ^b = 0 .

2 S1b   (s 2 + P)( s 3   s1) 2 s 2 b si e     I                            s e

¹       ( s 3 + P )( s , - s 2 ) ²

where s ₁ , s ₂ and s ₃ are the roots of the characteristic equation

2 e² x ³ + (2 e² P + c ) x ² + ( c P -2 - S ) x - Sp = 0 .

Denote the left hand side of the equation (11) by h(z), h (z) =- (s1 + P)

^V’     (s3 + P)( 51 - s 2)'

+ ^(s 2 ^{+ P)}(^s 3

-

s₁)

^(s3 ^{+ P)}(^s1 ^{- s}2)

2sz 2sz s₂e²+ s₃e³ ,

Moreover, s1 < -P< s₂< 0 < s₃.

Substituting (4) in the first term of equation (3), we have

BBB

—— + —²— + —³— = 0.

s1 + P  s₂+ P s₃+ P

From V² (0) = 0 , we have

B1 + B₂+ B₃= 0.

So, we obtain

Now we differentiate (12) with respect toz and get h,(z) = - (s1 + P)(s3 - s2) s 3esz

(s 3 + P)(s1 - s 2) ¹

+ ^(s 2 ^{+ P)(s} 3

-

s1)

^(s3 ^{+ P)(s}1 ^{- s}2)

In view of the calculation

3sz 3sz s 2 e2 + s 3 e 3 > 0.

^(s2 ^{+ P)(s}3 ^-s1)n B? =----------------B,,

²   (s3 + P)(S1 - s2) ³

lim h (z) = -to and lim h (z) = +to , z ^-to                      z ^|v

we can see that there exists a unique b s.t. h(b) = 0 .

If b > 0, such b is the optimal dividend barrier. If b< 0, then 0 is the dividend barrier.

Now we calculate

h(0) = - ⁽⁵1 + ^в)(53 ^{— 5}2)_2 + ⁽⁵2 + ^в)(53 ^{— 5}1)_2

^U     (53 + в)(51 - 52) 1   (53 + в)(51 — 52)2

+5 32

⁽⁵1 ^{— 5}3 ⁾⁽⁵2 ^{— 5}3 ⁾⁽⁵1 ^{+ 5}2 ^{+ 5}3 ^{+ в)}

=     —в     •

From (5), we have

51 + 5₂+ 53 = -(— 8 в + C) .

So, the fact 51 + 52 + 53 + в = —(— 8 в + c) + в implies b < 0 ^ h(0) > 0 ^ (2 82в + C) + в > 0, b > 0 ^ h (0) < 0 ^—(2 82 в + C) + в < 0.

If b< 0, the optimal dividend policy is that at time 0 , the initial capital x should be paid out. If b > 0 , whenever surplus goes above the level b , the excess is paid out as dividends.

From the above analysis, the solution to the problem is given by follows.

If —(2 8²в + c) + в > 0,

V2 (x) = x.

If—(2 8² в + C) + в< 0,

V²( x) 4

B1 e¹ + B₂e^{5 2 x} + B₃e^{5 3 x}, x—b + V₂( b),

0 < x< b, x > b.

where s₁, s₂and s₃are the roots of the characteristic equation (5), B₁, B₂and B₃are determined by (8), (9) and (10), b is determined by (11).

The above model makes stylized assumption that there are no transaction costs. Strictly speaking, the assumption is not satisfied in real applications. Now, we study the model where the transaction costs are proportional. If the company pays l as dividends, then the shareholders can get kl , k< 1 . In the meanwhile, (1 — k)l is the proportional transaction costs. In this case, we denote the value function byW(x). Repeat the procedure above, we obtain

W (x) = kV²( x).

Now we investigate how W(x) depends on k .

— W (x, k) = Be1 + R/2 x + R/3 x dk     12   3

= V²( x) > 0.

Note that the dividend barrier in the solution of this problem is the same as the barrier of the problem without proportional costs. In other words, proportional costs factor k has no effects on the dividend barrier.

v. The Solution of the control problem FOR THE CLASSICAL RISK MODEL WITH SOLVENCY CONSTRAINTS

An interesting discovery in [5] is the expression of the value function. That is,

V*(x,b) = hx), 0 < x< b. h'(b)

In what follows, we use this factorization formula that facilitates solving the optimal dividend problem with solvency constraints. The idea is inspired by [6].

Theorem 5.1. If h(x) is convex for x > b, cV1' (x) — (X + ^V\ x)

+X/X x — y )dF (y) < 0.

Proof. For any x > b1, b1< z< x, c Vx' (z) — (X + R)Vx( z) +XxV^X z — y )dF (y ) = 0, 0

and c V'; (z)—(X + 5)V1 (z) + X j0z Vb1 (z — y )dF (y)

= c (V1' — Vx' )(z) — (X + J)(V1 — Vx)( z)

+Xj₀z (V1 — Vx)(z — у )dF ( у )

= c (V1'— Vx")(--) — 5CV!— V')(--)

—Xj; (Kb, — V,')( z) — (V.1 — Vx')( z — У )dF (У)

< c (V1 ' — Vx" )(z).

(13 )

In fact, h (x) is convex on[bc, w) , therefore,

(V1"V,')'(У) = 1"hTy) >0, b.< y< x. ^b                  h (x)

(V¹_—V!)'( _y) = ^{h (y}) ^{( b 1 x ny} h'(b^T)

h (У ) h' ( x)

>0, y< b1.

Letting z ^ x on both sides of (13 ), we obtain cV'( x) — (X + S)V„1( x)

+Xj_|xVb1(x—y)dF(y) < 0.

Theorem 5.2 Assume the dividend policy {D_t¹} has to satisfy the solvency constraints for some positive b_c¹. b¹is the optimal barrier without restriction. Assume that h(x) is convex for x ≥ b¹. Then

• (a)    If b_c¹≤ b¹, the optimal policy is to use the barrier strategy at b¹.

• (b)    If b_c¹>b¹, the optimal policy is to use the barrier strategy at b_c¹.

Proof. Part (a) is obvious since the optimal policy is feasible under the constraint.

• (b) For any b₄>b₃≥b_c¹, we have

V¹(x,b4) < V¹(x,b3)

Indeed, forx >b₄>b₃,

• V¹ (x,b)=x-b+    ³,

^,33h′(b₃)^,

• V¹(x,b4)=x-b4+h(b⁴), h′(b₄)

• V¹(x,b)-V¹(x,b)=b-b+^h(b3)-^{h(b4) ,3,443}h′(b₃)h′(b₄)

  .

  
  

Let

h(b₃)    h(y)

j(y)=y-b+      -

• ³h′(b3) h′(b4)

  .

  
  

By simple calculation, j(b₃ )≥ 0and j′(y)≥ 0for b₄≥y≥b₃. Hence,

V¹(x,b3)-V¹(x,b4)=j(b4)≥0.

• V¹(x,b)=x-b+h(b³), ^,33h′(b₃)^,

• V¹(x,b)= h(x),

• ⁴    h′(b4)

• V¹(x,b)-V¹(x,b)=x-b+^h(b3)-^{h(x) ,3,43}h′(b3)h′(b4) =j(x)≥0.

  V¹ (x,b₃ )=

  
  

  V¹(x,b4)=

  
  

h(x) h′(b3)^, h(x) h′(b4)^,

V¹(x,b₃)-V¹(x,b₄)≥0.

So,

V¹(x) = maxV¹(x,b), ∀x ≥0 . ^c           b≥b₁

If the barrier strategy b_c¹is used, cVc¹′(x)-(λ+δ)Vc¹(x)

+λ ^xV¹(x-y)dF(y)=0, 0≤x<b¹. ₀c                                             c

From Theorem 5.1, cVc1′(x) -(λ+δ)Vc1(x)

+λ∫₀^xVc¹(x-y)dF(y)≤0, x≥bc¹.

_Vc1_(Xt1_∧Tπ)e-δ(t∧T^π)

_-           f

=Vc¹(x)+e^-δs[cVc¹′(Xs¹)-(λ+δ)Vc¹(Xs¹)

+λ ^Xs1-Vc¹(Xs¹--y)dF(y)]ds 0

∫t∧T^π

₀   e^-δsVc¹′(Xs¹)dDs^c

+∑ e^-δs[Vc¹(Xs¹--ΔDs¹)-Vc¹(Xs¹-)].(14) 0<s≤t∧T^π

Furthermore, applying the barrier strategyb_c¹,

• V_c¹(X_s¹_--ΔD_s¹)-V_c¹(X_s¹_-)=-ΔD_s¹. t∧T^π                                t∧T^π

  -∫₀e^-δsVc¹′(Xs¹)dDs^c=-∫₀e^-δsdDs^c

Therefore, taking expectation in (14), we have

E^t∧Tπe-δsdD1,c_≤V1(x)_-V1(X1 )e-δ(t∧T^π). ₀        ^{tc      c}   t∧T^π        .

Now letting t →∞ , it follows from bounded convergence theorem that

∫t∧T^π e^-δsdDt^1,c≤Vc¹(x).

The proof is completed.

• vi. The Solution of the control problem FOR THE CLASSICAL RISK MODEL perturbed by diffusion WITH SOLVENCY CONSTRAINTS

In this section, we can use the similar argument as section V.

Theorem 6.1. If h(x) is convex forx ≥ b_c², 2ε²Vc²′′(Xs^π)+cVc²′(x)-(λ+δ)Vc²(x) +λ ^xVc²(x-y)dF(y)≤0. 0

The proof is similar to the proof of Theorem 5.1.

Thereom 6.2. Assume the dividend policy {D_t² } has to satisfy the solvency constraints for some positive b_c². b²is the optimal barrier without restriction. Assume that h(x) is convex forx ≥ b². Then

• (a)    If b_c²≤ b², the optimal policy is to use the barrier strategy at b².

• (b)    Ifb_c²>b², the optimal policy is to use the barrier strategy at b_c².

Proof. Part (a) is obvious since the optimal policy is feasible under the constraint.

• (b) . As the corresponding part of Theorem 5.2, we have

• V²(x)=maxV²(x,b), ∀x≥0.

• ^c           b≥b2

If the barrier strategy b_c²is used,

12ε²Vc²′′(x) +cVc²′(x) -(λ+δ)Vc²(x)

+λ ^xV²(x-y)dF(y)=0, 0≤x<b². 0^{c                                              c}

From Theorem 6.1,

12ε²Vc²′′(x) +cVc²′(x) -(λ+δ)Vc²(x)

+λ ^xVc²(x-y)dF(y)≤0. x≥bc².

V_c2(X_t2_∧Tπ)e-δ(t∧T^π)

=Vc²(x)+^t∧Tπe^-δs[1ε²Vc²′′(Xs²)+cVc²′(Xs²) 02

X² -(λ+δ)Vc²(Xs²)+λ^s-Vc²(Xs²-0

-y)dF(y)]ds+^t∧Tπe^-δsVc²′(Xs²)dW 0

-∫₀^t∧Te^-δsVc²′(Xs²)dDs^c

+∑ e^-δs[Vc²(Xs²--ΔDs²)-Vc²(Xs²-)]. (15) 0<s≤t∧T^π

Furthermore, applying the barrier strategy b_c¹,

V_c²(X_s²_--ΔD_s²)-V_c²(X_s^π_-)=-ΔD_s².

_∫0t∧T

e^-δsV_c^2′(X_s²)dD_s^c=-∫^t∧Tπe^-δsdD_s^c.

Therefore, taking expectation in (14), we have E^t∧Tπe-δsdD2,c_≤V2(x)_-V2(X2 _π)e-δ(t∧T^π).

• ₀       ^{tc     c}  t∧T^π

Now letting t →∞ , it follows from bounded convergence theorem that

∫t∧T^π

• ₀    e^-δsdDt^2,c ≤ Vc²(x).

The proof is completed.