Сопоставление компьютерных реализаций равновесной и континуальной методик моделирования многофазных сред на примере одномерного нестационарного течения газовзвеси

Одной из задач компьютерных технологий является разработка программ компьютерного моделирования динамических процессов в механике жидкости и газа [1–22]. Несмотря на наличие различных пакетов моделирования, в том числе коммерческих, по-прежнему актуальным является разработка программ компьютерного моделирования течения сплошных сред. Одним из развивающихся разделов механики жидкости и газа является динамика неоднородных сред [4–6]. Основной сложностью моделирования таких процессов является учет взаимодействия компонент смеси или же учет влияния дисперсных компонент примеси на динамику несущей среды – жидкости или газа. В моделировании динамики неоднородных сред в литературе есть несколько подходов. Моделирование течений неоднородных сред как однородной жидкости или газа с добавлением коэффициентов, учитывающих неоднородность движущейся среды, – равновесный подход. В этом случае система уравнений движения включает в себя уравнения сохранения плотности, импульса и энергии для всей смеси в целом. Также моделирование динамики неоднородных сред возможно с помощью решения полной гидродинамической системы уравнений для каждой из компонент смеси с учетом взаимодействия компонент – континуальный подход моделирования динамики неоднородных сред. В данной работе проводится сопоставление равновесного и континуального подходов моделирования динамики неоднородных сред. В монографии [4] представлены теоретические основы моделирования динамики неоднородных сред. В монографиях [5, 6] представлены различные математические модели динамики запыленных сред, реализующие континуальную методику динамики неоднородных сред. В работе [7] в рамках акустического приближения рассматривались процессы распространения акустических возмущений в газокапельных средах с учетом конденсации капельной фазы. В исследовании [8] получена математическая модель течения двухкомпонентной сжимаемой смеси, моделировалось взаимодействие ударной волны с газокапельной взвесью. В публикации [9] численно моделировалась многофазное течение с фазовыми переходами. Модель состоит из уравнений динамики многокомпонентной невязкой среды. В работе [10] исследовалась неустойчивость тонкого слоя вязкой жидкости в линейном и нелинейном приближениях. Получены аналитические решения системы уравнений динамики сплошных сред. В работе [11] численно исследовано распространение цилиндрической ударной волны и ее взаимодействие с прилегающим слоем гетерогенной двухфазной среды. Получена технология, позволяющая проводить численное исследование динамики распространения цилиндрических ударных волн в областях, заполненных гетерогенными смесями. В публикации [12] рассматривались проблемы компьютерного моделирования течений в управляемых газоструйных системах и гидропневмоагрегатах, в конструкцию которых входят кольцевые сопла с различной геометрией в случае, когда движущаяся среда имеет многокомпонентный состав. В публикации [13] представлена математическая модель, использующая уравнение полной энергии, для численного исследования распространения ударных волн в гетерогенных двухфазных средах. Анализировались результаты расчетов течений аэрозолей, проведенных методами крупных частиц. В публикации [14] представлены расчеты в пакете ANSYS течения в проточной части вихревого расходомера. Исследовалась возможность оптимизации процесса расчетов течений в вихревом расходометре. В публикации [15] разработана равновесная модель односкоростной теплопроводной гетерогенной смеси, в которой учтен теплообмен между компонентами смеси. Для полученной математической модели разработан численный алгоритм решения методом Годунова.

Анализ литературы демонстрирует, что разработка компьютерных алгоритмов моделирования процессов гидрогазодинамики однородных и неоднородных сред на данный момент является актуальной проблемой компьютерных технологий. В данной работе проводятся расчеты одномерных течений неоднородной среды – газовзвеси, в которой масса дисперсной компоненты равна массе несущей среды. Расчеты проведены с помощью двух различных методик моделирования течений неоднородных сред, результаты расчетов сопоставляются. Новизна исследования заключается в сравнении параметров характеристик течений, описываемых разными методиками моделирования. Выявленные сопоставлением особенности методик моделирования течений газовзве-сей могут быть использованы при разработке компьютерных программ моделирования течений неоднородных сред.

Математическая модель

Для нестационарного течения c одномерной геометрией, уравнения движения газа можно записать в виде [1]:

ЗР + ^Н = 0;(1)

dtd

^(^u- + ^(pu2 + P -8ijt) = 0;

Ot

^i- + — fre + p — 8-t! u + 8tjX—) = 0.(3)

d t    d y ( ^L          j ^J ij d xJ

Здесь δ ij – символ Кронекера, течение вязкой среды описывается при δ 11 = 1, течение идеального газа при δ 12 = 0; p , ρ, u , Т , е –давление, плотность, скорость, температура и полная энергия газа. Равновесная модель динамики газовзвеси описывается системой уравнений [4]:

*' +8(peue) = 0;(4)

d td

M + £(p euE + PE ) = 0;(5)

tx

-(eE^ + ^([eE + PE ]UE ) = 0.

ot

В равновесной модели применяются те же обозначения, что и для однородного газа с индексом « E ». Для записи параметров системы используются следующие выражения:

^Р E 0 = ^{( 1 — a - p} 10 ^+ap 20^; T E = ^e E / ^C VE ^;

R E = ( 1 ^{— a} - P 10 R ( ( 1 ^-a - P 10 ^+a P 20 ) 1 ;

^p E ^=p E R E T E ^{; C} VE = c pE - R E ^; У E = ^C pE, ^C VE ^;

c pE = ( ( 1 ^-a - P 10 c p 1 ^+a P 20 c p 2 ) ( ( 1 ^-a - P 10 ^+a P 20 ) 1 ;

^ce = c ( 1 ^-a - P i0 Y e ( y ( 1 ^-a - P i0 ^+a YP 20 - ¹.

Здесь RE, R - газовые постоянные газа и смеси; cp1, cp2 – теплоемкости при постоянном давлении газа и дисперсной компоненты; cpE, cVE, cE - теплоемкость при постоянном давлении смеси, теплоемкость при постоянном объеме смеси, скорость звука в смеси; γ, γE – постоянная адиабаты газа и смеси; α, ρ10, ρ20 – объемное содержание, физическая плотность газа и дисперсной компо- ненты.

Континуальная математическая модель одномерного течения газовзвеси описывается системой уравнений:

5P 1 + ^{d (}P 1 ^u 1 ^- = 0;

dt      dx’

5(p1 u1 - d /     2       „ \     _d

---T"---+ ^“(p1 U1 + p -8ijT) = -F + a^“’ dt      dxx

⁺ , ^^ ^e 1 ^{+ p -8} у ^T ] ^u 1 ^{+ 8} y ^ ,¹ V^-8 j 2 ^- | F |^{( u} 1

d t    d y V                      d x )

—

u ₂

- — a

№,))

V   ^{d x}  J

se i +£ ( p 2 u 2)=0

d t      d x

^d(p 2 ^u 2 ^{-   d} /    2\_ _F     5p .

⁺a x ^{( P2 u 2 -}" F ^—aa x¹

-^e ²^ + — ( ^e 2 u ₂) = —8y Q .

d t     d x ^{( 2 2 -} ij

Индексами «1» и «2» обозначены физические параметры несущей и дисперсной фазы газо-взвеси. Здесь используются следующие обозначения:

^р 2 = ^а 2 ^р 20 ;

e 2 = ^р 2 C p 2 T 2^;

4 дu т = -ц —1;

3  д х

F = F + Рл + F "  ar ⁺ dA ⁺ am ’

F ar = A C^{d P 1 U 1}    u 21 ⁽ u ¹    u 2 ^{) ;}

4 d

(дu,       дu, । и ш  (д u   д u

F_am = 0,5ар₂     ¹ + u,    ¹

am Vet ¹ ex

—

д u ₂ д t

—

д u ) u 2         I ■ дx I

C d 2 = ^ j

( 24     4 )

V Re i2 ⁺Re i? J

+ 0,4;

M 12 = | ^u 1 ^u 21 / ^c ■

Re₁₂ = р 1 j u - u ₂ 1 d ц ^-1 ;

Pr = c_p цХ^{- 1} .

Здесь μ, λ, τ – вязкость, теплопроводность, функция учета вязкости; F am – сила присоединенных масс; F dA – динамическая сила Архимеда; F ar – сила аэродинамического сопротивления [4]; С_{d 2} – коэффициент сопротивления частицы; М ₁₂ – относительное число Маха; Re₁₂ – относительное число Рейнольдса; Pr – число Прандтля; ρ 2 – средняя плотность дисперсной фазы.

Для искомых функций задавались следующие граничные условия:

u i ( t ,1 ) = 0; u i ( t , У ) = 0; u 2 ( t ,1 ) = 0; u 2 ( t , У ) = 0;

e i ( t ,1 ) = e i ( t ,2 ) ; e 2 ( t ,1 ) = e 2 ( t ,2 ) ; e ( t , У ) = e i ( t , У -1 ) ; e 2 ( t , У ) = e 2 ( t , У -1 ) ;

P i ( t ,1 ) = P i ( t ,2 ) ; P 2 ( t ,1 ) = P 2 ( t ,2 ) ; р 1 ( t , У ) = P i ( t , У -1 ) ; P 2 ( t , У ) = P 2 ( t , У -1 ) .

Физическая область течения – отрезок [ a , b ] в переменных ( x , t ) отображается на единичный интервал [0, 1], в переменных (^, t ), ^ = ^( х ). В обобщенных координатах [1] система уравнений движения двухфазной двухтемпературной двухскоростной монодисперсной смеси (6)–(12) приобретает вид:

q t + e ₅ = H ; (13)

] Т ; J =5 x ;

J д^

q = [ P 1 , P 2 , P i u i , P 2 u 2 , e i , e 2

E =

J P₁ u ₁

J P 2 u 2

(     2        4

J P₂ u ₂

Je ₂ u ₂

;

Q

Система (13) решалась явным методом Мак-Кормака второго порядка [20] c последующим применением схемы нелинейной коррекции решения [21]. Явная схема Мак-Кормака включает в себя последовательно выполняемые шаги «предиктор» (14) и «корректор» (15):

q * = q П -A ( ^E n + i — E n ) + ^A ‘ ^H П ;

q n ^{+ 1} = ^0, 5( q n + q * ) - 0,5 A ( E * - E * . , ) + 0,5^A t H ‘ .

Здесь х(ξ) = Lξ + L0, J = L, в расчетах L0 = 0, Δξ = Δх/L = (L/(N – 1))/L - шаг по пространственному направлению; Δt – шаг по времени; N – количество узлов разбиения сетки. Шаг по времени выбирался исходя из условия Куранта – Фридрихса – Леви [1]. Для получения монотонного численного решения к сеточной функции на каждом временном шаге применялась схема нелинейной коррекции [2, 3]. Алгоритм коррекции выполнялся последовательно вдоль всех узлов на каждом временном слое. Рассмотрим алгоритм коррекции решения на примере функции f. В случае, если ВЫПОЛНЯЮТСЯ условия (5fj-1/2 • 8fj'+,2)< О или (8fj+V2 -8fj+3/2 )< 0, то к функции f в j-м узле применяется алгоритм схемы коррекции: fj = fj- +к(8fj+,2 -8fj-,2). Нижний индекс обозначает номер узла сетки. Здесь использованы обозначения: 8fj+,2 = fj+1 - fj, 8fj+32 = fj+2 - fj+1. В противном случае fj = fj, fj - значение функции в j-м узле после перехода на (n + 1)-й временной слой по схеме Мак-Кормака; κ – коэффициент коррекции.

Программная реализация

Численный алгоритм реализован в виде программного комплекса. Изменения в структуре численно интегрируемых уравнений позволяют проводить расчеты как для идеальной математической модели, так и для вязкой теплопроводной среды. Компьютерная реализация численной модели течения жидкости или газа состоит из следующих частей: определение геометрических параметров физической области течения, в одномерном случае только размеров области, формирование разбиения области моделирования, задание граничных условий и непосредственно самого процесса численного интегрирования системы аэрогидродинамических уравнений. В данной работе компьютерная программа написана на языке программирования Fortran. Программный код, составляющий компьютерную модель, представляет собой набор последовательно реализуемых компонент. Алгоритм программной реализации численной модели динамики газовзвеси имеет следующую последовательность:

• 1)    задаются физические параметры газа и твердых частиц;

• 2)    из файлов считываются начальные значения функций, геометрия области и характеристики ее сеточного разбиения;

• 3)    строится сеточное разбиение области течения смеси;

• 4)    определяется значение величин межфазного обмена импульсом и межфазного теплообмена;

• 5)    реализуется конечно-разностное решение уравнений динамики смеси;

• 6)    проводится нелинейная коррекция сеточных функций;

• 7)    значения искомых функций в узлах сетки на каждом временном слое выводятся в файл.

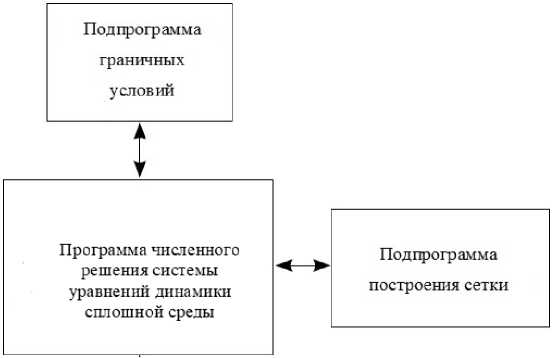
Вычисление значений параметров неоднородной среды на каждом последующем временном слое осуществляется последовательным применением шагов 4–6. Программный комплекс состоит из нескольких компонент: подпрограмма задания граничных условий, подпрограмма формирования конечно-разностного разбиения физической области, основная программа расчета динамики неоднородной среды.

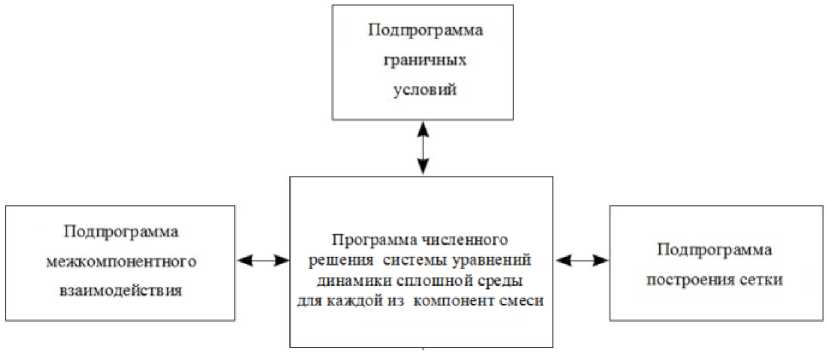
На рис. 1а изображена структура программы моделирования динамики однофазной сплошной среды. На рис. 1b представлена структура программы численного моделирования динамики неоднородной среды, реализующей континуальную методику моделирования неоднородной среды. В структуре программы численной реализации континуальной методики моделирования динамики неоднородных сред присутствует два отличия: в основной программе численно интегрируется полная гидродинамическая система уравнений для всей совокупности компонент смеси, также присутствует подпрограмма учета межфазного взаимодействия.

а)

b)

Рис. 1. Схема программы численного моделирования течения однородной среды (а) и многофазной среды, реализующей континуальную методику моделирования динамики неоднородных сред (b)

Fig. 1. Scheme of the program for numerical simulation of the flow of a homogeneous medium (а) and of a multiphase medium, which implements the continuum method for modeling the dynamics of inhomogeneous media (b)

Результаты расчетов

Для сопоставления различных моделей динамики многофазных сред рассматривался процесс распада разрыва [21] в газовзвеси [5, 6].

Предполагалось, что канал разделен разделяющей поверхностью на две части: в одной половине давление газа p 1 = 100 кПа, в другой части канала давление газа – p 2 , р 2 >  p 1 (рис. 2). После разрушения разделяющей поверхности формируется ударная волна, движущаяся из области с высоким давлением в область с низким давлением, при этом происходит изменение физических параметров газа. Длина канала L = 10 м, количество узлов сетки N = 500. Несущая среда описывалась как воздух. Физическая плотность материала дисперсной компоненты и теплоемкость материала дисперсной компоненты составляла ρ 20 = 2500 кг/м³, С p 1 = 903 Дж/кг·К, объемное содержание α = 0,0005, дисперсность частиц d = 2 мкм.

Pl                                  ■ pi >Р1

Рис. 2. Схематическое изображение начального момента распада прямого скачка уплотнения в газовзвеси Fig. 2. Schematic representation of the initial moment of the collapse of a direct shock wave in a gas suspension

В процессе распространения ударной волны в газе происходит существенное изменение плотности газа [21] (рис. 3).

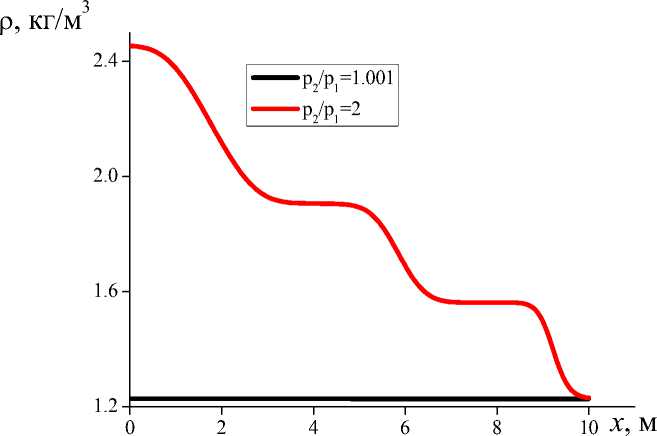
Рис. 3. Пространственное распределение плотности газа при различных интенсивностях распада разрыва в однородном газе

Fig. 3. Spatial distribution of gas density at different intensities of discontinuity decay in a homogeneous gas

На рис. 4 изображено пространственное распределение скорости газа при моделировании процесса распада разрыва при интенсивности разрыва ( p 2 – p 1 )/ p 1 = 0,001. В полученных расчетах отличие скоростей газа, полученных по модели идеального и вязкого теплопроводного газа составляет | u i – u v | ≈ 10 % u i .

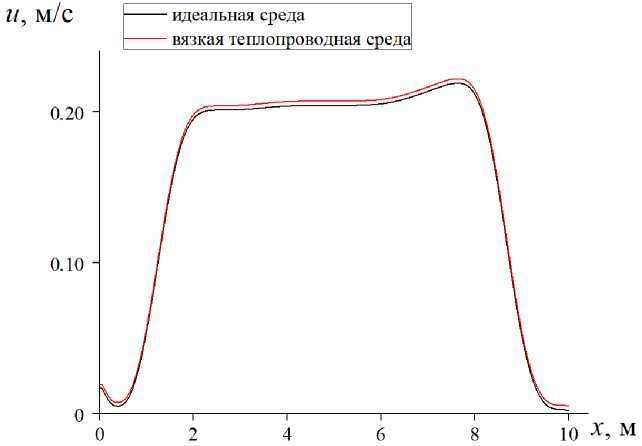
Рис. 4. Пространственное распределение скорости газа в однородном газе для различных моделей динамики газа, момент времени t = 15 мс, интенсивность перепада давлений р ₂/ р 1 = 1,001

Fig. 4. Spatial distribution of gas velocity in a homogeneous gas for various models of gas dynamics, time t = 15 ms, intensity of pressure drop р ₂/ р 1 = 1.001

При этом для ударно-волнового течения ( p 2 – p 1 )/ p 1 = 1 различия для скоростей, полученных по двум различным моделям динамики газа, не являются существенными (рис. 5).

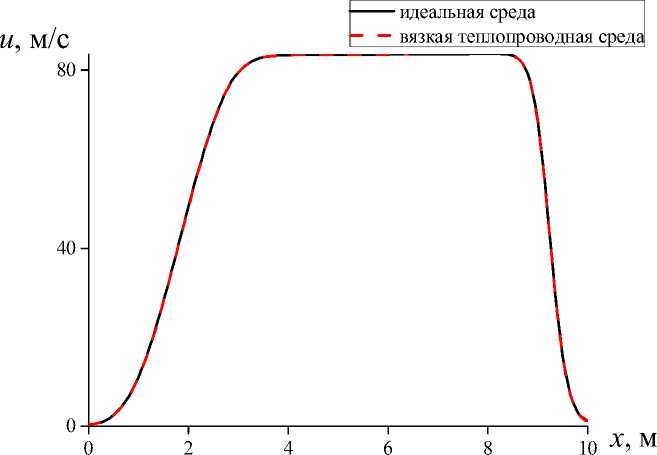
Рис. 5. Пространственное распределение скорости газа в однородном газе для различных моделей динамики газа, момент времени t = 12 мс, интенсивность перепада давлений р 2 / р 1 = 2

Fig. 5. Spatial distribution of gas velocity in a homogeneous gas for various models of gas dynamics, time t = 12 ms, intensity of pressure drop р 2 / р 1 = 2

В абсолютных значениях разность скоростей между вязким теплопроводным и идеальным газом возрастает вместе со скоростью течения, но составляет не более | u i – u v |/ u i ≈ 0,5 % от скорости движения газа u_i в ударно-волновом течении (рис. 6). Для течений с различными интенсивностями распределение плотности газа существенно отличается, при малых интенсивностях течений возможно пренебречь изменениями плотности среды, тогда как для ударно-волнового течения изменения в плотности среды более существенны (см. рис. 6).

|u-u |, м/c

0.40

0.35

0.30

0.25

0.20

0.15

0.10

0.05

0.00 4------------- 1--------------1--------------1-------------- г

^^^^^^интенсивность p ₂/ p ₁=1.001

<     интенсивность p ₂/ p ₁=2

x , м

Рис. 6. Пространственное распределение модуля разности скоростей газа, вычисленных при моделировании динамики однородного газа моделью вязкого теплопроводного газа и идеального газа, t = 12 мс

• Fig. 6.    Spatial distribution of the modulus of the difference in gas velocities calculated when modeling the dynamics of a homogeneous gas with a model of a viscous heat-conducting gas and an ideal gas, t = 12 ms

100.8 100.6 100.4 100.2 100.0

Отличие континуальной и равновесной моделей динамики газовзвесей заключается в том, что при моделировании движения однородной среды и динамики несущей фазы газовзвеси в континуальной модели начальные распределения давления газа совпадают, тогда как в равновесной модели при тех же параметрах несущей среды начальное давление газа имеет меньшее значение (рис. 7). Давление газа при моделировании динамики газовзвеси равновесной моделью составляет 99,95 % от давления в однородном газе или газовой фазе, моделируемой континуальной моделью. Отличием континуальной модели динамики многофазных сред является наличие температурной неравновестности. Даже при равной начальной температуре фаз в процессе движения газовзвеси формируется разность температур несущей и дисперсной фазы газовзвеси.

p , кПа 101.0

^^^^^^в равновесная модель

^^^^^^в однородный газ

• • • континуальная модель

0        2        4        6        8        10 x , м

Рис. 7. Начальные распределения давления при моделировании распада разрыва в однородном газе и в газовзвеси при динамике газовзвеси континуальной и равновесной моделях при одинаковых начальных параметрах газа

• Fig. 7.    Initial pressure distributions in modeling the discontinuity decay in a homogeneous gas and in a gas suspension with the gas suspension dynamics by the continuum and equilibrium models for the same initial gas parameters

  На рис. 8 представлено сопоставление модуля разности температуры несущей и дисперсной компоненты для двух различных интенсивностей перепада давления р 2 / p 1 = 1,01, p 2 / p 1 = 2. Даже при малых интенсивностях течений (см. рис. 8), в континуальной модели с вязкой и теплопроводной несущей средой и несущей средой - идеальным газом существенно отличаются температуры газовой и дисперсной фаз смеси. Для начального перепада давлений p 2 / p 1 = 2 для несущей среды -идеального газа величина разности температур фаз существенно больше - | T 1 – T 2 | = 14,32 К, чем если модель учитывает вязкость и теплопроводность среды - | T ₁ – T ₂| = 0,35 К. Для начального перепада давлений p 2 / p 1 = 1,01 в модели с несущей средой - идеальным газом величина интенсивности разности температур - | T ₁ – T ₂| = 0,23 К, если модель учитывает вязкость и теплопроводность несущей среды тот же параметр - | T 1 – T 2 | = 0,0026 К.

Равновесная модель, как и модель динамики идеального газа, позволяет получить аналитические решения [21]. Сопоставление численных расчетов, полученных как для однородной идеальной среды, так и для равновесной модели динамики газовзвеси, демонстрирует приемлемое соответствие 75 % от аналогичных аналитических решений, что связано с диссипацией численного решения [1, 5, 6] (рис. 9).

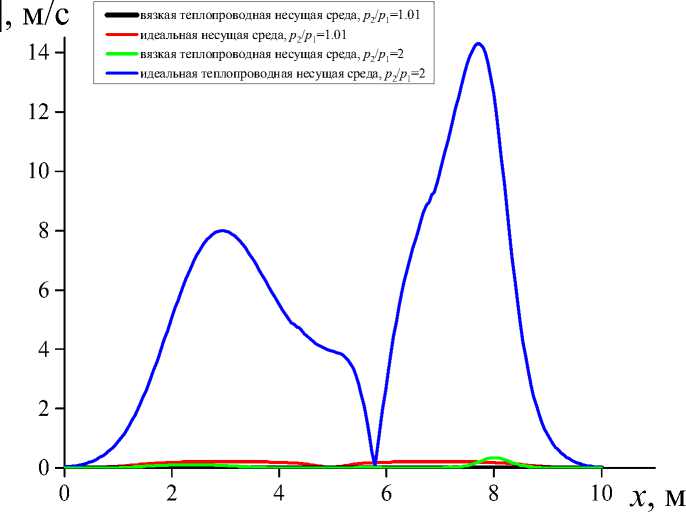
Рис. 8. Пространственное распределение модуля разности температуры фаз при моделировании динамики газовзвеси континуальными моделями с вязкой теплопроводной и идеальной несущей средой для разных интенсивностей начального перепада давлений

Fig. 8. Spatial distribution of phase temperature difference modulus when modeling gas suspension dynamics by continual models with a viscous heat-conducting and ideal carrier medium for different intensities of the initial pressure drop

10 x, м

Рис. 9. Сопоставление численных расчетов – сплошной линией и аналитических расчетов – пунктирной линией. Интенсивность начального перепада давления р 2 / р 1 = 1,1

• Fig. 9.    Comparison of numerical calculations – a solid line and analytical calculations – a dotted line. The intensity of the initial pressure drop р ₂/ р ₁ = 1.1

101.0

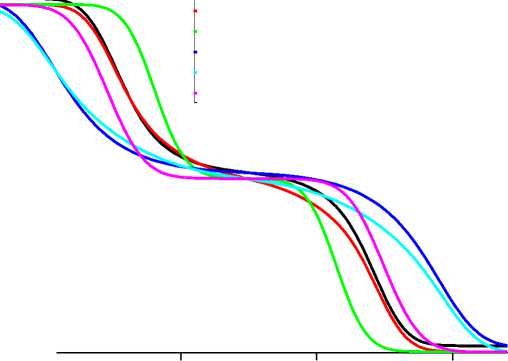
На рис. 10 представлены результаты численных расчетов давления и температуры газа в газо-взвеси при интенсивности распада разрыва давления (p2 – p1)/p1 = 0,01 в два различных момента времени - t = 5 мс и t = 8 мс, из рис. 10 следует, что наибольшая скорость распространения ударной волны наблюдается в равновесной модели, меньшая скорость наблюдается в континуальной модели с идеальной несущей средой, еще меньшая скорость распространения в ударной волне с вязкой теплопроводной средой (см. рис. 10а). При этом, чем выше скорость распространения возмущения, тем меньше температура газа, достигаемая в ударной волне, наименьшая скорость и наибольшая температура газа в модели динамики газовзвеси с вязкой теплопроводной средой (см. рис. 10b).

p, кПа

t , K

^^^^^^^^^* равновесная модель, t =6 мс

^^^^^^^^^^ модель с идеальной несущей средой, t =6 мс

^^^^^^^^^^ модель с вязкой несущей средой, t =6 мс

^^^^^^^^^^ равновесная модель,t=9 мс модель с идеальной несущей средой,t=9 мс

^^^^^^^™ модель с вязкой несущей средой, t =9 мс

100.5

100.0

• ^{4            6            8}    x , м

293.4 293.2 293.0 292.8 292.6

a)

равновесная модель,t=6 мс модель с идеальной несущей средой,t=6 мс модель с вязкой несущей средой,t=6 мс равновесная модель,t=9 мс модель с идеальной несущей средой,t=9 мс модель с вязкой несущей средой,t=9 мс

2            4            6            8    x , м

b)

Рис. 10. Пространственные распределения в различные моменты времени давления газа (а) и температуры газа (b) при моделировании динамики газовзвеси различными математическими моделями

Fig. 10. Spatial distributions at different times of gas pressure (а) and gas temperature (b) when modeling the dynamics of a gas suspension by various mathematical models

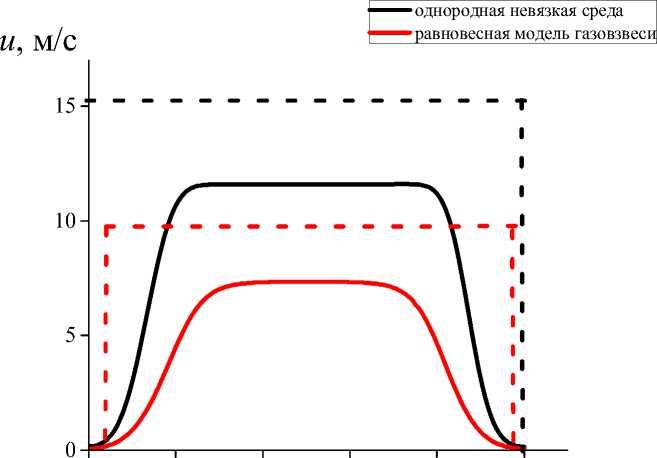
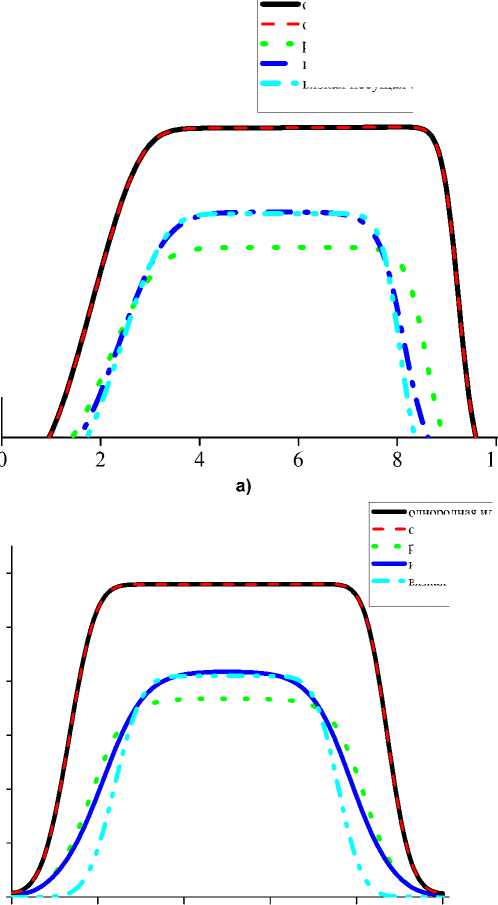
При уменьшении интенсивности течения увеличиваются различия в результатах расчетов скорости однородного газа и скорости газовой фазы в газовзвеси, а также скорости среды в равновесной модели (рис. 11). Для интенсивностей начального перепада давления р2/p1 = 2, р2/p1 = 1,1, р2/p1 = 1,01 отношения к максимальной скорости идеального однородного газа (uig) максимальной скорости газа в континуальной модели динамики газовзвеси с идеальной средой -ugsi/uig, газовзвеси с вязкой теплопроводной несущей средой -ugsv/uig, максимальной скорости среды в равновесной модели газовзвеси - ugse/uig (см. таблицу). Из таблицы следует, что наиболее существенно скорость течения газа в газовзвеси уменьшается относительно однородной идеальной среды (при той же интенсивности начального перепада давления) для расчетов течения газо-взвеси континуальной методикой моделирования с вязкой теплопроводной средой, менее интенсивно скорость среды уменьшается в равновесной модели, еще меньше уменьшается в континуальной модели с идеальной средой.

u, м/c

u, м/c

однородная идеальная среда однородная вязкая среда равновесная модель идеальная несущая среда вязкая несущая среда

10 x , м

однородная идеальная среда однородная вязкая среда равновесная модель идеальная несущая среда вязкая несущая среда

b)

1x0, м

Рис. 11. Пространственное распределение скорости газа при моделировании распада разрыва в однородном газе и в газовзвеси равновесной и континуальной математическими моделями при начальной интенсивности разрыва давлений р ₂/ р ₁ = 2 (а); р ₂/ р ₁ = 1,1 (b); р ₂/ р ₁ = 1,01 (c)

Fig. 11. Spatial distribution of gas velocity when modeling discontinuity decay in a homogeneous gas and in a gas suspension by equilibrium and continuum mathematical models at the initial intensity of pressure discontinuity р ₂/ р ₁ = 2 (а); р 2 / р 1 = 1.1 (b); р 2 / р 1 = 1.01 (c) (см. также с. 72)

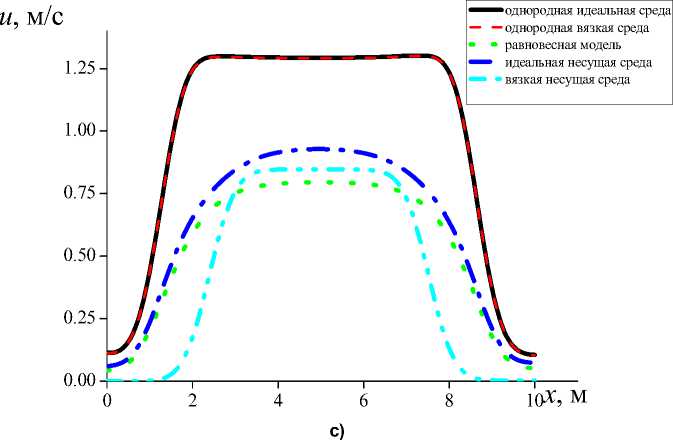
Рис. 11. Окончание

Fig. 11. End

Отношения максимальных значений скоростей несущей среды Ratios of the maximum values of the carrier medium

р 2 / p 1	u gsi / u ig	u gsv / u ig	u gse / u ig
р 2 / p 1 = 2	76,86 %	75,17 %	69,68 %
р 2 / p 1 = 1,1	72 %	70 %	63,28 %
р 2 / p 1 = 1,01	71 %	64 %	60,5 %

Выводы

В данной работе представлены сопоставления расчетов численных реализаций математических моделей одномерных течений газовзвесей. Сопоставлялись равновесная методика моделирования динамики многофазной среды с континуальной методикой моделирования динамики многофазных сред, в рамках которой были получены модели, описывающие несущею фазу смеси как идеальный газ и как вязкую теплопроводную среду. Определено, что наибольшая скорость распространения возмущения в газовзвеси наблюдается в равновесной модели, меньшая скорость распространения – в континуальной модели с идеальной средой, наименьшая скорость наблюдается в газовзвеси с вязкой теплопроводной средой. Выявлено, что при различных интенсивностях течений наличие дисперсной фазы в смеси оказывает различное влияние. Полученные закономерности возможно использовать при разработке компьютерных моделей динамики многофазных сред.