Сопряжение каркасно-кинематических поверхностей сплайнами четвертой степени

В инженерной геометрии объекты можно разделить на следующие типы: примитивы, тела сложной формы, тела сложной структуры, тела сложной структуры и формы. Поверхности – тела, поверхности которых описываются единым уравнением: простые многогранники, шары, цилиндры и конусы вращения. В технике в чистом виде примитивы встречаются редко. Чаще всего они являются компонентами тел сложной структуры. Это основная масса деталей современной техники. Примерами могут служить болт, ступенчатый или коленчатый вал и т. п. Тела сложной формы имеют сложную криволинейную поверхность, получаемую, как правило, методами интерполяции полиномами или иногда другими функциями. Тела сложной структуры и формы состоят из нескольких тел сложной формы. Поверхности этих тел должны быть, как правило, гладко состыкованы [1]. Гладкое соединение таких поверхностей – важная и трудоемкая задача инженерной геометрии [2–4]. Примером являются зализы – поверхности сопряжения поверхностей агрегатов летательных аппаратов (мотогандола – пилон – крыло, крыло – фюзеляж и т. п.) [5, 6] и подобные им поверхности в судостроении [7, 8] и автомобилестроении.

Существует несколько способов конструирования сопрягающей поверхности [8–12]. Не существует универсального метода. Выбор метода за- висит в первую очередь от сопрягаемых поверхностей [1, 13, 14]. Если сопрягающиеся поверхности имеют разнородные структуры, зализ удобно конструировать как огибающую семейства сфер переменного радиуса, касательных к двум сопрягаемым поверхностям одновременно [15, 16]. При этом линия касания сферы и заданных поверхностей формирует отсек сопрягаемой поверхности. Если поверхности сопрягаются по заданным кромкам и их структуры одинаковы (например, кусочно-гладкие поверхности с одинаковым количеством кусков вдоль кромок), то поверхности можно соединить сопрягающей той же структуры.

К сопрягающей, как правило, предъявляются те же требования, что и к исходным поверхностям – гладкость, плавность, отсутствие перегибов, ограничение на минимальный радиус и др. [17, 18]. Если полученная поверхность не удовлетворяет каким-то требованиям, необходимо внести изменения. Удобство метода конструирования кроме всего прочего заключается в том, чтобы вносить эти изменения локально, на определенных участках, без значительных изменений остальной поверхности и по возможности без пересчета поверхности [2, 3].

Основная часть

Предлагается использовать в качестве сопрягающей кинематическую поверхность зависимых сечений с направляющими, кромками сопрягаемых поверхностей и интегродифференциальным сплайном четвертой степени в качестве образующей [19-21].

Звено сплайна описывается уравнением в векторной форме

V ( u ) = V 1 P 1 ( и ) + V ₂ P ₂ ( и ) +

⁺ ( ^V M⁽ и ) ⁺ V W и ) ) h ^{+ 1} Ф 5⁽ и )/ h ,        (1)

IV'+V где h = —-—,   ф1 (и) = (1 + 5и)(1 - 3и)(1 - и)2,

Ф ₂ ( и ) = (3 и - 2)(6 - 5 и ) и ² ,

Ф ₃( и ) = и (2 - 5 и )(1 - и ) ² /2,

Ф ₄ ( и ) = (1 - и )(3 - 5 и ) и ² /2, ф ₅ ( и ) = 30 и ² (1 - и ) ² , где V и V^ - радиус-векторы начала и конца дуги, Ф! ( и ) - базисные функции, параметр и е [0,1]. Вектор I i характеризует прогиб кривой (рис. 1).

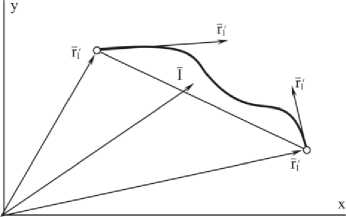
Рис. 1. Дуга кривой четвертого порядка

Он указывает на центр массы неплоского сечения, ограниченного дугой и хордой. Векторы V' и V ₂' - касательные. Таким образом, дуга задается пятью параметрами, а не четырьмя, как обычный кубический сплайн. Пятый параметр - вектор I i задает полноту кривой и послужит для локальной модификации кривой и далее поверхности.

У обычного кубического сплайна нет коэффициентов для локального изменения формы одного участка составной кривой. Составная кривая строится путем расчета первых производных во внутренних узлах сплайна из условия непрерывности вторых производных в этих узлах сплайна при заданных краевых условиях. Если изменить касательную в одном из внутренних узлов, то изменятся два примыкающих участка. Также на границах участка нарушается второй порядок гладкости, то есть вторая производная терпит разрыв в трех узлах (рис. 2).

Если понадобится соединить две кривые одной единственной дугой кубического сплайна, необходимыми исходными данными такой задачи являются координаты соединяемых концов дуг и значения первых производных на этих концах. Составная кривая имеет первый порядок гладкости. Имеется возможность ограниченного управления формой кривой. Для этого нужно изменить длины касательных векторов, не изменяя их направления (рис. 3).

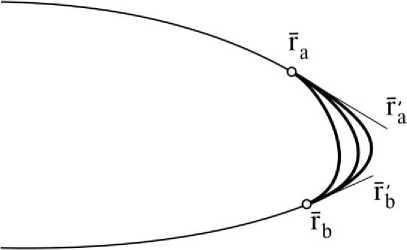
Рис. 3. Соединение двух кривых дугой кубического сплайна

Предлагается более удобный способ конструирования замыкающей кривой с возможностью управления ее формой.

Пусть заданы две дуги разных кривых линий. Требуется соединить конечные точки кривых сплайном четвертой степени. Потребуются радиус-векторы концов дуг r ‘ и r ‘ , а также вектора касательных на концах дуг r ‘ и r ‘ . Для построения сопрягающей дуги потребуется вектор-интеграл I. Первые четыре коэффициента r , r_b , r ‘ и r ‘ заданы. Вектор I , определяющий полноту дуги, не задан. Это величина переменная и подбирается в итерационном режиме. Но на начальном этапе конструирования ему надо задать начальное значение. Будем считать, что концы дуг r _a и r ^ соединяются одним звеном кубического сплайна -вектор-функции V ₂( и ) с компонентами:

S 2 ( и ),

V ₂( и ) = <^ ( и ),

S Z ( и ).

Интегрируем скалярные сплайн-функции по и и получаем компоненты вектор-интеграла

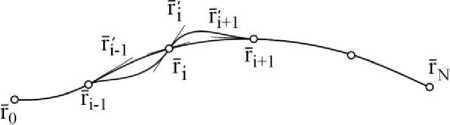
Рис. 2. Изменение формы кривой касательной на внутреннем узле кубического сплайна

b                      hh

Ix = J S3x (и) du = (Sx + Sb) h + (Sbx + Sbx);

a b                        h               h2, (2)

^b a

•1, =J S3 (и) du = (Sy + Sb) h + (Sby + S'by)   ;, 1’

a b                    , h            „h z      zz     zz

I z = J ^S 3 ^{( и} ) ^du = ^{( S} a ^{+ S} b )^ ^{+ ( S} a ^{+ S} b )^,

a

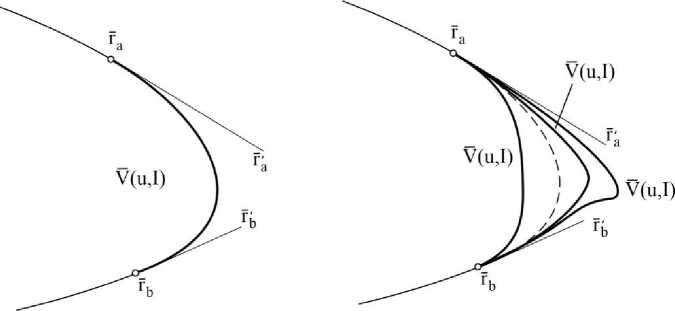
а)                                                 б)

Рис. 4. Зависимость формы кривой от интегрального коэффициента

где Sa, Sbx, Sa, Sy, Saz, Sb - координаты конечных xxyyzz точек, Sa , Sb , Sa , Sy , Sa , Sb — компоненты касательных векторов, h – параметр сплайна. Он оказывает некоторое влияние на форму сплайна. Его нужно задать приблизительно из расчета h = V(Sax - Sb )2 + (Say - Sb )2 + (SZa — Si )2 •  (3)

Строим сплайн (рис. 4а)

V ^{( u} ) = r a Ф 1 ^(u ) ⁺ r b Ф 2 ^{( u} ) ⁺

⁺( ^Ф з С u ) ⁺ r >4 ( u ) ) h ⁺ I Ф 5⁽ u )/ h .                ⁽⁴⁾

Далее, оперируя вектором I , можно изменять форму кривой (рис. 4б).

Пусть даны два куска одной или разных поверхностей. Пусть задача состоит в том, чтобы гладко соединить их по границам некоторой сопрягающей поверхностью. Для сопряжения рассматриваемым способом нужны линии на поверхности – границы кусков. Также должны быть заданные на этих линиях вектора, касательные к поверхности в направлении, топологически перпендикулярном границам a и b (рис. 5).

Сопрягающая поверхность строится как кинематическая поверхность с двумя направляющими. Образующей будет являться сплайн (4). Для построения поверхности необходимо задать взаимнооднозначное соответствие между двумя направляющими (если его еще нет), например, приведением обеих направляющих к одному параметру v . Все пять векторов, задающих образующую, теперь будут являться функцией от v . Первые четыре вектор функции задаются простым приравниванием

• V 1 ⁽ v ) = r a ⁽ v ),

• V 2 ^{( v} ) = r b ^{( v} ),

V v ) = ±ф( uv ),                     ⁽⁵⁾

d u

• -    d -

• ' '( v) = — *( uv),

I        d u

Интегральный параметр I ( u ) изначально задается как (2). К каждому скалярному компоненту вектор-функции I ( v ) добавим корректирующий элемент A I_x ( v ), A I y ( v ) и A I_z ( v ) соответственно. Окончательно

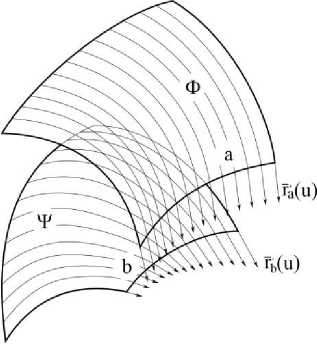
Рис. 5. Исходные данные для задачи сопряжения поверхностей

b a

= •

, h ,        , h ²

I_x = ( S ax ( v ) + S b ( v )) - + ( S ax ( v ) + S bx ( v )) - + A I x ( v );

I y = ( S ay ( v ) + S b ( v )) - + ( S a^y ( v ) + S b^y ( v )) - + A I y ( v );

I_z = ( S^z _a ( v ) + S₆^z ( v )) - + ( S ‘ ^z ( v ) + S ‘ ^z ( v )) — + A I _z ( v ). zab  ab   z

Корректирующие компоненты выделим в дельную функцию

A I x ( v ),

A I b^a ( v ) = Iy (v),

A I_z ( v ).

от-

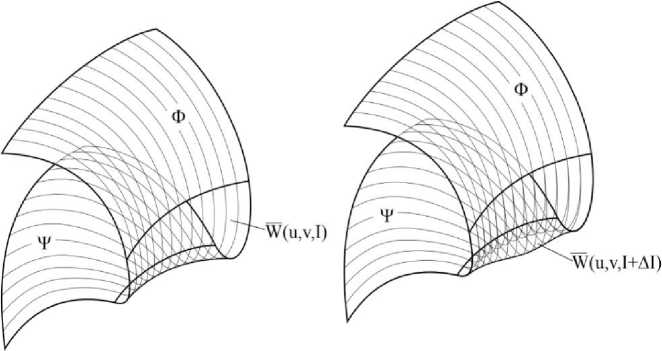
Окончательно поверхность имеет вид (рис. 6а):

W ( u ) = F a ( v ) Ф 1 ( u ) + r , ( v ) Ф 2 ( u ) +

+ ( r a ⁽ v ) Ф з ⁽ u ) + r a ⁽ v ) Ф 4 ⁽ u ) ) h +

+ ( I ( v ) + A I ( v )) Ф 5 ( u )/ h .                      (8)

а)                                   б)

Рис. 6. Окончательный вид сопрягающихся поверхностей

В системе автоматизированного проектирования, изменяя эту функцию, можно интерактивно управлять формой сопрягающей поверхности (рис. 6б). Можно задать ее единым уравнением или заменить кусочно-гладкой функцией, например сплайном.

Рассмотрим другой пример. Пусть конструируется тело сложной структуры, содержащей две поверхности сложной формы. Поверхность Ф типа «обтекатель» задается семейством параллельных сечений и интерполируется бикубическим сплайном. Поверхность У задана аналогичным образом. Причем сечения двух поверхностей расположены попарно в одних плоскостях так, чтобы можно было два сечения разных поверхностей, расположенные в одной плоскости гладко состыковать в единую линию объединенной поверхности (рис. 7).

Наметим линию касания на a на поверхности Ф и такую же линию b на поверхности У . Строим интегродифференциальный сплайн (4) для каждой пары сечений (рис. 8).

V ^{( и} ) = r i Ф 1 ⁽ и ) + ^ГыФ 2 ^(и ) ⁺ ( r i Ф з ^{( и} ) + r bt Ф 4 ^{( и} ) ) h +

+ 1ф ф ₅( и )/ h , i = 0,..., N.                        (9)

Теперь приводим параметры линий а и b к единому параметру v и интерполируем пять коэффициентов сплайна (4). Практически полученная поверхность является неоднородным (гетерогенным) сплайном, состоящим из кубических сплайнов в направлении v и единственного звена сплайна четвертой степени в направлении и :

Wi = ^( и) Gt/ (v), (10) где ( -    - д V.     д VK        ^ VV ди       ди       1 G = * ai+1         * bi+1 ау ау - ai+1           bi+1      j ди        ди       i+1 , 5Г 8У ai             bi д2 Vai     д2 Vbi     дIi д v     Bv ди 0v   дид v    0v ЗУ BV С f ai+1     u F bi+1 В 2V    d2V    BI F ai+1          F bi+1         i+1 Idv    Bv ди Bv   дид v    Bv 9 i = 0,... ,N-1, ф(и) - матрица весовых функций четвертой степени (1), ф(и) - матрица аналогичных весовых функций кубического сплайна. Последний столбец в матрице (10) представляет со-

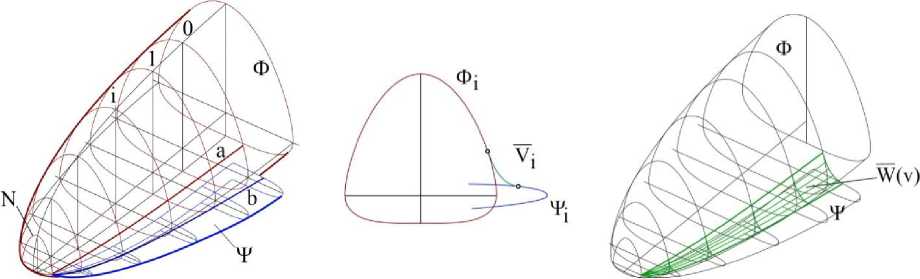
Рис. 7. Комбинируемая поверхность, заданная бикубическими сплайнами

Рис. 8. Гладкая стыковка поверхностей

бой сплайн, интерполирующий узловые значения I , i = 0,..., N. При помощи этой функции можно изменять форму сопрягающей поверхности.

Выводы

Предложенный алгоритм представляет собой удобный инструмент для решения важнейшей задачи инженерной геометрии – конструирования сопрягающей поверхности промышленных изделий геометрически сложной структуры и формы. Метод прост и удобен, использует минимальное число входных параметров. Алгоритм легко программируется. При воспроизведении на компьютере метод нагляден. При небольшой дальнейшей доработке рассмотренным инструментом можно дополнить существующие системы автоматизированного проектирования для решения указанных и некоторых других задач.