Сортировка пучков Лагерра-Гаусса по радиальному числу посредством моментов интенсивности

Уникальное свойство пучков Лагерра–Гаусса (ЛГ) переносить оптические вихри, а следовательно, и орбитальный угловой момент (ОУМ), вызвало интенсивную волну как теоретических, так и экспериментальных исследований [1–4]. Ключевым моментом исследований явилось решение проблемы сортировки пучков ЛГ из оптического массива по азимутальному числу m (по топологическому заряду) и измерение его величины, что стало одной из отправных точек дальнейшего развития сингулярной оптики. Заметим, что задача сортировки и синтеза лазерных пучков была поставлена и частично решена В. Сойфером и М. Голубом на основе метода компьютерных голографических решёток (см., например, [5–9] в списке литературы) задолго до начала исследований оптических вихрей. Неожиданный рывок исследований сортировки вихревых пучков по топологическому заряду произошел в начале XXI столетия, когда персональные быстродействующие компьютеры стали надёжным инструментом учёных. Именно тогда были усовершенствованы голографические технологии и созданы устройства формирования голограмм в реальном времени [10–13], развиты новые специальные подхо- ды астигматических преобразований [14, 15] и методы моментов интенсивности высших порядков [16– 19], а также созданы специальные оптические транспаранты [20], которые в сочетании с интерферометрическими устройствами [21] позволяют быстро оценивать состояния вихревых пучков.

Повышенный интерес к топологическому заряду оптических вихрей затенил исследования свойств массивов пучков ЛГ с различными радиальными числами n , которые отвечают за число нулей поля в радиальном направлении (за число кольцевых дислокаций) в каждой вихревой моде. И только недавние исследования процессов уплотнения информационных массивов [22] и поиск оптимальных квантовых ключей в криптографии [23] показали, что дальнейшее совершенствование соответствующих оптических систем возможно, главным образом, за счёт увеличения числа степеней свободы оптических сигналов, а именно за счёт сортировки пучков по радиальным числам n [24].

Анализ проблемы показал, что сортировку модовых пучков Лагерра–Гаусса, Эрмита–Гаусса и Бесселя–Гаусса по радиальному числу можно осуществлять с помощью метода компьютерных голографических решёток [10–13]. Теоретические разработки ключевых физических принципов сортировки мод [20, 25–27] были подкреплены рядом экспериментов [28–32]. Особый метод сортировки мод с помощью управления фазой Гуи каждой модой ЛГ был предложен в работе [29] и экспериментально воплощён в работе [30]. Указанный метод разрабатывался с целью дальнейшего использования в компактных оптоэлектронных устройствах. Основными элементами оптической установки являлись два интерферометра (либо Маха–Цендера, либо Саньяка). Первый интерферометр осуществлял компенсацию фазы Гуи модовых пучков, а второй интерферометр предназначался для конечного этапа сортировки мод.

Более простой и надёжный метод сортировки мод по топологическому заряду, с нашей точки зрения, был предложен авторами работ [16–19], ключевой идеей которого явилось использование метода моментов интенсивности высших порядков для цифровой сортировки вихревых мод по топологическому заряду. Цифровая сортировка мод предполагает измерение спектра квадратов модовых амплитуд и фаз с последующим воспроизведением модовых пучков. Дополнительная корректировка алгоритма сортировки мод по азимутальному индексу позволит распространить этот подход на сортировку мод по радиальному числу.

Предположим, что нам удалось разработать и воплотить упомянутый метод сортировки мод. Но если исходный пучок содержит массив мод ЛГ и, предположим, что этот массив подвергается простому возмущению посредством диафрагмы с круговым отверстием, то каждая мода в массиве порождает широкий спектр вторичных ЛГ мод. Тогда каждому радиальному числу в спектре мод будет соответствовать множество вторичных мод. Спектр оказывается вырожденным по радиальному числу. Сразу возникает вопрос: как сортировать моды комбинированного пучка? Эта проблема ранее не исследовалась. Таким образом, целью данной статьи явилась разработка и воплощение метода сортировки мод по радиальному индексу с учётом вырождения на основе подхода моментов интенсивности высших порядков.

1. Предварительные замечания

В общем случае нашей задачей является исследование структуры пучка Лагерра–Гаусса, подверженного возмущению при прохождении через непрозрачный экран, отверстие в котором описывается апертурной функцией f ( р , ф ), где р и ф являются радиальной и азимутальной полярными координатами соответственно. Тогда комплексную амплитуду возмущённого пучка ЛГ запишем в виде

^ m , n = f ( Г , ф ) ф m , n ( Г , ф , Z ) , (1) где амплитудная функция модового пучка есть

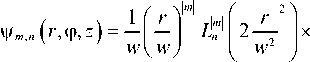
exp ( im ф + i Г _m , n ) exp

r ²

□

r = р / w 0 - безразмерный радиус, w 0 - радиус перетяжки пучка в исходной плоскости z = 0, L m ( x ) - многочлены Лагерра, m и n >0 – азимутальное (топологический заряд) и радиальное число, □ =1- iz / z ₀ , w =| g |, z ₀ = kw 2 /2, Г m,n ( z ) = (2 n + m + 1)arctg z / z о - фаза Гуи, k – волновое число. Топологический заряд m отвечает за ОУМ модового пучка, являясь собственным значением оператора углового момента. Число n =0, 1, 2... характеризует дополнительные степени свободы пучка ЛГ и было названо «внутренним зарядом гиперболического момента» [26], как собственное значение соответствующего оператора.

Основным предметом нашего анализа является распределение интенсивности возмущённого пучка 3 ₀₀ ( r , ф ) = Y ( r , ф ) ^ * ( r , ф ), которое включает в себя полную информацию о модовом составе пучка (амплитуде и фазе мод) и действующем возмущении.

Нашей главной задачей является извлечение этой информации на эксперименте. Мы уже показали [16– 18], что локальное возмущение голографической решётки может вызвать лавину оптических вихрей, спектр которой охватывает вихри как с положительными m >0, так и с отрицательными m <0 топологическими зарядами, что вызывает резкое снижение ОУМ. В то же время секторное возмущение вихревого пучка почти не изменяет ОУМ в широком диапазоне углов диафрагмы, но резко снижает его, когда диафрагма оставляет только узкую щель для пучка [21].

Чтобы воспользоваться методом моментов интенсивности, разложим возмущённый пучок в ряд по ортогональному базису пучков Лагерра–Гаусса:

= ZZ C

да

да

, is ф

exp

р ²

w ²

где амплитуды мод C m,n,s,k задаются соотношением

C m , n , s , _к = J ^ m , n _V S , k d S                                  (4)

R в плоскости z = 0 и Ym,n =f (р, ф) фm,n(р, ф).

В нашей работе мы сосредоточимся на возмущении пучка ЛГ диафрагмой с круговой апертурой, ось которой совпадает с осью пучка. Очевидно, что в этом случае интеграл (4) оставит единственный член с m = s , т.е. топологический заряд не изменяется при действии возмущения ( m = const).

2. Принципы цифровой сортировки мод ЛГ

Прежде чем анализировать возмущение пучка, при котором моды с одинаковыми радиальными чис-

лами в спектре амплитуд интерферируют друг с другом (вырожденные состояния пучка), остановимся на простейшем невырожденном состоянии, когда единичный пучок ЛГ проходит через диафрагму с круговым отверстием с функцией пропускания

1,0 <  r <  R , 0, r >  R .

В этом случае диафрагма не вводит дополнительную фазу, а амплитуда (5) является действительной функцией. Фактически, диафрагма действует как возмущение, вызывающее рождение широкого спектра мод ЛГ, который можно представить в виде разложения по ортогональному базису пучков Лагерра–Гаусса как

to

= £Cm.n,krmLm (2r2)eimф exp(-r2), k=0

радиальными индексами k , что удобно представить в виде спектра квадратов модовых амплитуд C m,n , k ( k , R ) , представленного на рис. 1.

Даже небольшие изменения величины возмущения R приводят к резким изменениям формы спектра для различных радиальных чисел n в виде перераспределения энергии между модами, что можно заметить, сравнивая рис. 1 а и 1 б . Важно отметить, что каждому радиальному числу k соответствует только одна мода при любом возмущении R . Это значит, что спектр не вырожден относительно радиального числа k , что способствует единообразной сортировке модовых пучков по радиальному числу. Однако спектр квадратов амплитуд не позволяет определить знаки модовых амплитуд. Поэтому для выполнения сортировки мод нам потребуется также измерять перекрёстные члены в распределении интенсивности возмущённого пучка.

где амплитуды мод определяются согласно (4) в виде

m , n , k

R

J * ( r , ф ) v m , k ( r , ф ) r d r 0

to                      2

а)

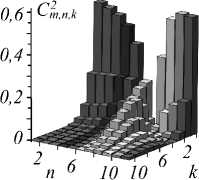
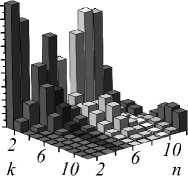
Рис. 1. Спектры квадратов амплитуд C _m ² _,n,k (n,k) для m = 3

^т,п,к 0,8

0,6

0,4

0,2

б)

и являются действительными числами. Раскрывая выражение (7), находим

и различных радиусов отверстия диафрагмы R = 1 (а), R = 2 (б). Спектр C _m ² _,n,k (n,k) задаёт вызванную возмущением сортировку мод ЛГ по радиальному числу k

c .

m , n , k

⁽ m ⁺ 1 ) n      1

2 ^j j ! n ! ( m + j + 1 )

x ( 2 R 2 ) m ^{+ j + 1}

x ₂ F 2 ( m + n + 1, m + j + 1; m + 1, m + j + 2; - (2 R )²

здесь использовался интеграл [33]

X                   (m +1)

[x ² e ^- x Lm (x ) d x = — ---- n-x ²⁺¹

совместно с представлением многочлена Лагерра

k

Lm (x )=E(-0 j j=0

m + k ^ x j k - j J j ! ,

где 2 F 2 – гипергеометрическая функция. Амплитуды мод ЛГ C m,n,k задаются тройкой целых чисел: m – исходный топологический заряд вихря, n > 0 – исходное радиальное число, k > 0 – радиальное число моды ЛГ в спектре амплитуд (6). Топологический заряд m не участвует в суммировании в (6), а следовательно, ОУМ возмущённого пучка не изменяется. Действие возмущения сводится к расщеплению единичного пучка с радиальным числом n на множество пучков с

при условии, что исходный ЛГ – пучок имеет топологический заряд m (и равный ему ОУМI z = m = 3) и радиальное число n (число кольцевых дислокаций)

Используя преобразование Френеля для ЛГ – пучка в плоскости z =0 [9], можно записать вид комплексной амплитуды в произвольной плоскости z = const:

V m , n ( r , ф , Z )

to m.n,k

o ( z ) k =0

r

w(z)

2 m r

^X L k 2 2 / \

e ^m Ф+ i г m , k ( z ) exp

,

где c ( z )=1- iz / z 0 , z ₀ = kw 2 /2, w ( z ) = | c ( z )|, Г m,n ( z ) = (2 n + m + 1) arctg z / z 0 – фаза Гуи, k – волновое число.

Нашей основной задачей является экспериментальная сортировка ЛГ-мод возмущённого пучка по радиальному числу. С этой целью мы воспользуемся методом моментов интенсивности J p,q высших порядков [16,34] в виде

J p , q = J M p , q ( r , ф ) 3 m , n ( r ) d 5 , R

где 3 m,n ( r , Ф , z = 0) = | V m,n ( r , z = 0)|² - распределение интенсивности в плоскости z = 0, M pq ( r , ф ) - функция мо-

ментов, интегрирование проводится по всей плоскости поперечного сечения модового пучка, p, q =0, 1,2, .... Поскольку распределение интенсивности 3m,n(r) является радиально симметричной функцией, то функцию моментов удобно выбрать в аналогичном виде Mp,q(r). Запишем распределение интенсивности в виде от 2

^ m, n   / m k=0

| V m,k ( r )| 2 +

от

^{+ 2} ^^ C m , n , k ^C m , n , s ^V m , k ^V m , s ^. k , s =0, k * s

Для оптимального выбора вида функции моментов M p,q в (12) необходимо, прежде всего, воспользоваться характерными свойствами амплитуд C m,n,k в спектре (11). В качестве примера на рис. 2 а приведено распределение модовых амплитуд C m,n,k по радиальному числу k , построенному в соответствии с уравнением (8). Во-первых, амплитуды мод быстро уменьшаются по мере роста радиального числа. Это значит, что сумму в выражении (13) можно прервать на некотором числе k max = N , скажем, при C m2,_n , N >  0,001. Во-вторых, в спектре наблюдается чередование знаков амплитуд, что указывает на необходимость измерения перекрёстных амплитуд. В-третьих, зависимость С m ² , n , k ( R ) на рис. 2 б

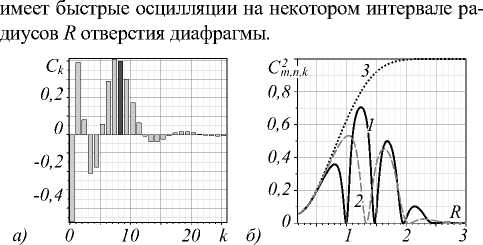
Рис. 2. Спектр модовых амплитуд C m,n (k) по радиальному числу k ЛГ – пучка с числами m = 3, n = 8, возмущённого круговой апертурой R = 2 (а); зависимость квадратов амплитуд C _m ² _,n,k (R) от радиуса R радиальных чисел, (1) k = 6, (2) k = 3, (3) k = 0 при начальных числах пучка m = 3, n = 6 (б)

Наличие этих осцилляций накладывает жёсткие ограничения на выбор функции моментов M p,q . Как мы покажем ниже, неудачный выбор функции моментов неизбежно приводит к большой величине ошибки измерений спектров и сортировки пучков.

Заметим, что определение (12) момента интенсивности можно рассматривать как систему линейных уравнений относительно квадратов амплитуд Cm2,n,k и перекрёстных амплитуд 2Cm,n,kCm,n,s. Действительно, члены правой части уравнения (12) с учётом (13) зависят от квадратов амплитуд, перекрёстных амплитуд и множителей, которые легко вычислить от jpq = JГ 2m+1 Mp,qLm (2r2)Lm (2r2)e-2r2dr .        (14)

Правая часть уравнения представляет собой также интеграл, который определяется на эксперименте. Сначала сканируется произведение экспериментально измеренного распределения интенсивности на функцию момента 3 exp ( r ) M _pq , а затем вычисляется интеграл. Получаем систему линейных уравнений относительно переменных X p = C m 2, n , k и Y p = 2 C m,nk C mn,s . Число уравнений задаётся числом квадратов амплитуд и перекрёстных амплитуд. Если число квадратов амплитуд равно N , а число перекрёстных амплитуд задаётся числом сочетаний N !/(2! ( N – 2)!), то полное число уравнений равно

N total

= N +

N !

2! ( N - 2 ) ! ^.

Введём обозначение вектор-столбца

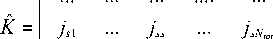
₄ j Nt„ 1     ...    Jn„s    ...     j N .t,N.t, v

и окончательно запишем матричное уравнение в виде

J = ТС X .                                       (17)

Его символическое решение есть

X = К ^{- 1} J .                                      (18)

Однако обратная матрица КС-1 может быть определена только тогда, когда det К ^ 0 . Но это только необходимое условие. Достаточным условием является требование минимальности ошибки измерений компонент вектора X. Выполнение как необходимого, так и достаточного условия зависят от оптимального выбора функции момента Mp,q. Поясним это. В работе [19] при измерении спектра вихрей в пучке с невырожденным составом оптических вихрей (когда топологический заряд в спектре мод может быть только положительным или отрицательным) достаточно было ограничиться выбором функции момента в виде ортогонального базиса многочленов Лагерра. Иная ситуация сложилась при измерении спектра вихрей в пучке с вырожденным составом вихрей (различные знаки топологических зарядов) в работе [20]. Здесь пришлось сначала подвергать пучок астигматичному преобразованию, чтобы снять вырождение по топологическому заряду, и представлять распределение интенсивности в базисе многочленов Эрмита, а затем использовать преобразование Фурье для Mp,q, чтобы система уравнений стала разрешённой, а ошибка измерений снизилась до 0,03.

В данной статье топологический заряд постоянный, и мы сначала выбрали функцию M p,q в базисе многочленов Лагерра. При этом система уравнений не замыкалась. Затем мы воспользовались функцией моментов, определяющей преобразование Фурье:

M p , q

sin pr cos qr

Хотя теперь система уравнений замкнулась (det С * 0), ошибка измерений в модельном эксперименте могла достигать 70 % при произвольном выборе чисел p * q . Единственный вариант, при котором ошибка измерений снизилась до 1 %, сводился к требованию p = q = 1,3, 5, ....

Важным элементом процесса цифровой сортировки мод является определение знаков перекрёстных амплитуд Y s и каждой амплитуды в отдельности. Для того, чтобы определить знак любой модовой амплитуды в спектре, достаточно знать знак амплитуды невозмущённого пучка. Далее знаки вычисляются, например, по цепочке

• Y 0 ^ ... ^ Y n -1 ^ Y n ^ Y n +1 ^ ... ^ Y V„ , .

• 3.    Сортировка невырожденных состояний

  При экспериментальной сортировке мод в возмущённом пучке мы сначала детально исследовали сортировку мод единичного ЛГ-пучка (невырожденный случай), а затем распространили метод на сложный пучок (вырожденный случай), содержащий несколько исходных ЛГ-пучков с одинаковыми топологическими зарядами m , но различными радиальными числами n . Эксперимент проводился на экспериментальной установке, блок-схема которой приведена на рис. 3. Гауссов пучок ( TEM 00 мода) излучался He–Ne лазером ( X = 0,6328 мкм), проходил через пространственный фильтр P-FF, где проводилась пространственная фильтрация пучка и согласование его параметров с параметрами рабочей ячейки SLM модулятора типа Thorlabs EXULUS-4K1. Пространственный модулятор позволял формировать ЛГ-пучки с топологическим зарядом m <70 и радиальным числом n < 50. Регулировка размеров отверстия диафрагмы R осуществлялась посредством ограничения размеров голографической решётки на SLM-модуляторе. Отражённый от голографической решётки пучок расщеплялся на два плеча делительной призмой BS. В первом плече возмущённый пучок фокусировался сферической линзой L ( f sph = 10 см) на входное окно CCD– камеры, расположенное в фокальной плоскости линзы. Второе плечо предназначалось для проверки топологического заряда и ОУМ пучка. Для этого использовалась цилиндрическая линза CL с фокусным расстоянием f cyl =20 см. ОУМ регистрировался в

фокальной плоскости цилиндрической линзы в соответствии с методикой, подробно изложенной в работах [15, 16, 35]. Оценка топологического заряда основывается на наших предварительных экспериментах и теоретических исследованиях авторов работы [36].

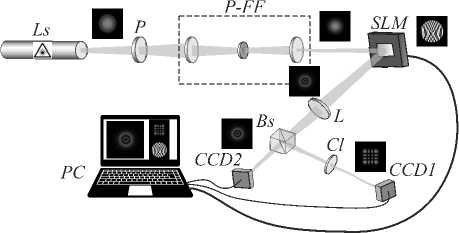
Рис. 3. Блок-схема экспериментальной установки для измерения спектра вихрей и цифровой сортировки LG – пучков. P – поляризатор, P-FF – пространственный фильтр, SLM – пространственный модулятор света,

L – сферическая линза, BS – делительная призма, CL – цилиндрическая линза, CCD – детектор пучка

Мы обнаружили, что астигматическое преобразование с помощью цилиндрической линзы преобразует единичный пучок ЛГ в плоскости двойного фокуса в пучок Эрмита–Гаусса с числом нулей интенсивности (скажем, для m >0) m + n вдоль оси x и n нулей в ортогональном направлении. Исследования измерения топологического заряда для пучков ЛГ с нулевым радиальным числом ( n =0) были детально рассмотрены в работе [14]. Рассмотрим алгоритм цифровой сортировки мод ЛГ, возникших в результате возмущения единичного пучка ЛГ, схема которого приведена на рис. 4.

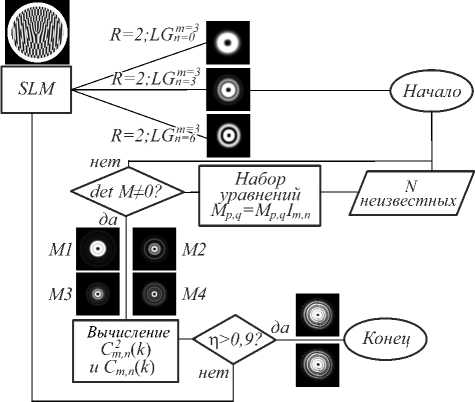
Рис. 4. Алгоритм цифровой сортировки ЛГ – мод по радиальным числам

Сначала сканируется распределение интенсивности 3exp, формируется массив из Mp,q=Mp,q3exp и рассчитывается следующий массив моментов интенсивности Jp,q для каждого значения индексов p и q. Эти вычисления позволяют задать вектор J в правой части уравнения (18). Следующим шагом является формирование матрицы Mˆ в (16) и нахождение её детерминанта. Если det Ml = 0 , то включается обратная связь и алгоритм требует уточнения вида функций момента Mp,q, если же det Ml * 0 , то программа продолжает работу.

Далее матрица M p,q и вектор J подставляются в уравнение (18), уравнения решаются, формируется массив компонент вектора X и строится спектр квадратов амплитуд С _m ² _{, n} ( k ). Следующий шаг – вычисление знаков цепочки перекрёстных амплитуд и построение спектра амплитуд C m,n ( k ). Далее формируется комплексная амплитуда V mp_n в (6) из отсортированных мод ЛГ, включается второй контур обратной связи и формируется дифракционная решётка с функцией пропускания

T x = signum [ cos ( arg ^ m » — Qr cos ф ) ] ,      (19)

где Q – масштабный множитель. Голографическая решётка формируется на рабочем элементе SLM– модулятора, а лазерный пучок восстанавливает вторичный пучок как результат сортировки мод первичного возмущённого пучка, и его распределение интенсивности 32xp сканируется. Сравнение распределений интенсивности 32xp и 3exp осуществлялось посредством степени корреляции от

J 3 exp ( r ) 3 2x ^p r d r

" от .                        (20)

J 3 exp ( r ) r d r J ^T p ( r ) r d r

а)

0,8

0,6

0,4

0,2

б)

Рис. 5. Спектр амплитуд C m,n (k) пучка ЛГ с топологическим зарядом, возмущенного диафрагмой с R = 2 для различных исходных радиальных чисел: n = 0 (а), n = 3 (б), n = 6 (в) и n = 8 (г). На выноске показаны распределения интенсивности 3 ™,n (r) соответствующих возмущённых пучков ЛГ. Амплитуды мод с исходными радиальными числами окрашены тёмно-серым

10 15 20

10 15 к

г)

в)

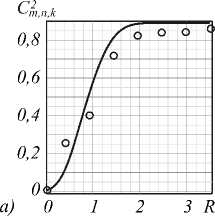
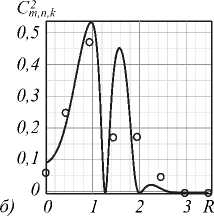
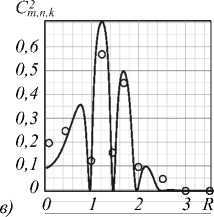
Рис. 6. Вклад различных мод возмущённых ЛГ – пучков с исходным топологическим зарядом m = 3 и радиальными числами n = 0 (а), n = 3 (б) и n = 6 (в) в компоненту k = 0 спектра квадратов амплитуд C _m ² _,n,k (R) для различных радиусов R.

Сплошные линии – теория, кружки – эксперимент

Если степень корреляции оказывается меньше заданного оптимального значения n < 0,9, процесс сортировки прерывается, а экспериментальная установка подвергается дополнительной юстировке. В противном случае ( n >  0,9) на экран монитора выводился спектр квадрата амплитуды, спектр C m,n ( k ), амплитуды C m,n ( k ) и информационная энтропия H m,n . Этих данных вполне достаточно, чтобы восстановить с высокой степенью точности каждую из ЛГ – мод в отдельности и возмущённый пучок в целом.

Спектр амплитуд C m,n ( k ) на рис. 5, полученный на эксперименте, описывает характерные черты ЛГ -пучка с топологическим зарядом m =3, но с различными радиальными числами n =0, n =3, n =6 и n = 8, возмущённого диафрагмой с радиусом отверстия

R =2. Вихревой пучок с радиальным числом n =0 на рис. 5 а не испытывает существенных структурных изменений, не считая появления двух соседних мод с малыми амплитудами, фазы которых сдвинуты на п . Заметный отклик на возмущение возникает по мере роста величины радиального числа, так что энергия быстро перераспределяется среди большого числа мод с бинарными скачками фаз 0 и п на рис. 5 б-г .

Более общая картина С m ² , n , k ( R ) перераспределения энергии и вклада различных пучков с n =0, n =3 и n =6 в спектральное состояние k =0 для разных радиусов R приведена на рис. 6.

Монотонное снижение энергии от Ст,n,k = 1 до С^,n,k = 0,1 на рис. 6а указывает на постепенный отток энергии из k =0 спектральной компоненты и её перераспределение среди других спектральных компонент по мере уменьшения радиуса R апертуры. В то же время энергия перетекает из модовых компонент высших порядков (рис. 6б, в) в k =0 моду. Однако отток энергии из мод высших порядков неравномерен, квадраты амплитуд испытывают осцилляции. Интересно отметить, что максимум кривой С32,3,0 max вклада n =3 пучка в k =0 моду на рис. 6б соответствует нулям многочлена Лагерра

L3 (2r2) = 0 ^rmx = Rо «(1,035; 1,63; 2,3), а минимальный вклад С323-0 = 0 приходится на экстремумы многочленов Лагерра

-d L 3 ( 2 r ² ) = 0 ^ г о = R max « ( 1,33; 2,06 ) .

d r

Аналогичная ситуация наблюдается и для возмущенного n =6 пучка на рис. 6 в . Перекачка энергии из высших гармоник ( m , n ) в k -ю моду прекращается, когда радиус апертуры R достигает критического радиуса пятна исходного пучка R _cr = r spot = V2 n + m + 1 [37]. Как видно из рис. 6, наблюдается небольшое рассогласование экспериментальных точек и компьютерного моделирования. Такое рассогласование эксперимента и расчёта связано, с нашей точки зрения, с отклонениями экспериментального распределения интенсивности 3 _exp e_r ( r , ф ) от осевой симметрии. Это указывает на необходимость включения обратной связи в алгоритм сортировки мод для дополнительной юстировки оптической системы. Однако, как мы покажем ниже, отмеченное рассогласование не превышает требований к оптимальной степени корреляции п рассортированных пучков в данном случае.

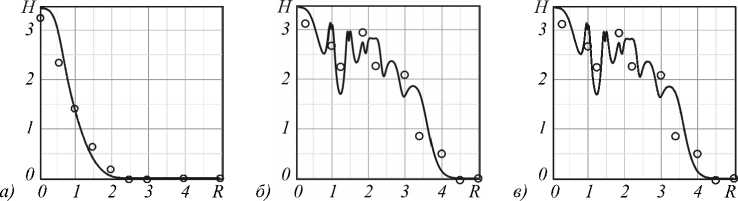
Рис. 7. Зависимость энтропии H m,n от радиуса апертуры R для различных исходных пучков ЛГ с одинаковыми топологическими зарядами m = 3, но различными радиальными числами n = 0 (a), n = 3 (б), n = 6 (в).

Сплошные линии – теория, кружки – эксперимент

Возрастание неопределённости в возмущённом пучке может быть оценено с помощью информационной энтропии H m,n (энтропии Шеннона) [38]. Чтобы найти энтропию H m,n в нашем случае, прежде всего заметим, что нормированный квадрат амплитуды C n е (0,1) в разложении (2) можно трактовать как условную вероятность P ( k / n ) встретить вихревой пучок в состоянии | к ) среди N состояний при условии, что внешнее возмущение R подействовало на пучок в состоянии | n ) , т.е. P ( к / n ) = C m2,_n ( R , к ). Такой подход учёта беспорядка вихревых состояний позволяет использовать формулу Шеннона [39] в виде

N

H m , n = - £ P ( к / П ) log 2 P ( к / n ) = к =0 N

= - y c m,n ( R , к ) log 2 c m , n ( R , к ) > 0, к =0

где энтропия измеряется в битах. С другой стороны, энтропию H m,n можно рассматривать как меру новой информации, которая появилась в пучке в результате действия возмущения пучка ЛГ. Эта интерпретация оказывается полезной для совершенствования квантовых криптографических систем, поскольку позволяет просто создавать требуемые распределения квантовых ключей [40].

Также важно отметить , что энтропия H m,n задается исключительно спектром квадратов амплитуд. Рис. 7 иллюстрирует возрастание неопределённости исходных состояний (3,0), (3,3) и (3,6) в виде зависимости H m,n ( R ). Все три состояния пучка характеризуются аналогичным типом эволюции энтропии: высокая величина энтропии H m,n соответствует малым радиусам апертуры R и её снижению до нуля при больших радиусах. Однако если энтропия состояния (3,0) испытывает монотонное снижение по мере увеличения радиуса возмущения R , то состояния (3,3) и (3,6) сопровождаются быстрыми осцилляциями, которые замечены на эксперименте.

Окончательным этапом процесса цифровой сортировки мод по радиальному числу является формирование комбинированного пучка с помощью спектра амплитуд C m,n,k на рис. 5 и рис. 6, который сопровождается формированием цифровой голограммы в жидкокристаллической ячейке SLM-модулятора и воспроизведением реального комбинированного пучка с оптимальной степенью корреляции п = 0,94.

Результат такой сортировки пучков демонстрирует рис. 8.

• 4.    Сортировка вырожденных состояний

Основным предметом исследований систем передачи и обработки оптической информации является смесь световых пучков с различными амплитудами и фазами [38]. В данном параграфе мы упростили задачу и выбрали невозмущённую комбинацию ЛГ-пучков с действительными амплитудами An без начальных фаз, возмущённую круглой апертурой. По аналогии с возмущением единичного пучка в параграфе 2 (11), запишем комплексную амплитуду смеси в виде

MN

X ££ A m , C

r ²

——+ im ф e ^{ct( z} )

G( z )

r

r

^ m /   ,2

J Я2^J

e ^r m . k ⁽ z ) ,

где M – полное число ЛГ – пучков. Из (22) видно, что каждой k -й компоненте соответствует M ЛГ – мод с амплитудами A m,n , т.е. каждая компонента спектра имеет M –кратное вырождение. Для того чтобы снять вырождение, необходимо подвергнуть пучок соответствующему преобразованию. Насколько нам известно, в настоящее время таких исследований не проводилось.

Физический аспект проблемы сортировки вырожденных пучков заключается в следующем. Каждую вырожденную k -ю моду волнового поля (22) запишем в виде

( m )

V т, k ( Г, ф, Z ) = |Z AnCm - n - k |v m, k ( Г, ф, Z ) , (23) x n=0 / где vm,k(r, ф, z) - комплексная амплитуда k-го пучка ЛГ. На эксперименте требуется отсортировать каждую такую моду. Но функция поля vm,k(r, ф, z) определяется только двумя числами – m и k, а в сортировке должно участвовать ещё исходное радиальное число n. Очевидно, что рассмотренный выше подход не позволяет выполнить такую операцию. Для этого необходимо поставить метку на амплитуду An, например, в виде дополнительной модуляции амплитуды или начальной фазы. Мы воспользуемся более простым методом, рассмотренным ниже.

Без потери общности ограничимся простым случаем сложного исходного пучка, содержащего три M =3 моды ЛГ с радиальными числами n 1 =0, n 2 =3, n 3 =6, но с одинаковыми топологическими зарядами m =3. Действие диафрагмы с круговым отверстием R приводит к возникновению широкого спектра вторичных мод ЛГ C m ( k ) для каждого исходного пучка ЛГ с индивидуальными спектрами C m,n₁ ( k ), C m,n₂ ( k ) и C m,n₃ ( k ), которые в общем случае перекрывают друг друга. Каждая k -я мода оказывается трижды вырожденной.

б)

Рис. 8. Распределение интенсивности (инверсия) 3 (r, ф) вихревого пучка с топологическим зарядом m = 3 и радиальным числом n = 6, возмущённого круговой апертурой R = 2,5: исходный возмущённый пучок (а), пучок, восстановленный с помощью цифровой сортировки мод (б), компьютерное моделирование возмущённого пучка (в). Степень корреляции изображений (а) и (б) составляет h = 0,94

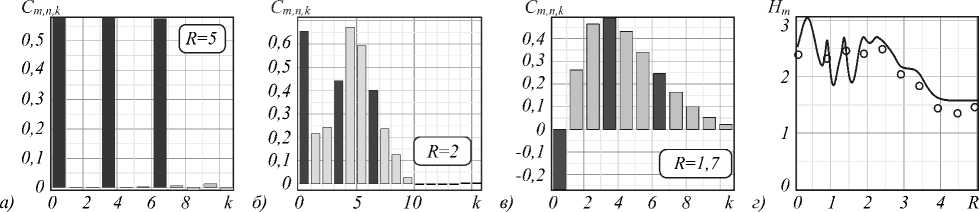
Рис. 9. Динамика ЛГ-мод (а, б, в) в вырожденном спектре мод C m,k с радиальными числами n 1 = 0, n 2 = 3, и n 3 = 6 соответственно, вызванная изменением радиуса апертуры R; энтропия H m (R) сложного пучка (г);

непрерывная линия – теория, эксперимент – кружки

Для компьютерного моделирования и реальной сортировки пучков можно воспользоваться алгоритмом, рассмотренным ранее, с учётом суммы в выражении (22). Однако спектр амплитуд содержит вырожденные моды. В случае невозмущённого пучка ( R ^к ) каждая спектральная амплитуда записывается в виде

M m •k ^ n=0 n , как показано на рис. 9а. На рисунке все три моды имеют почти одинаковые амплитуды в пределах ошибки измерений. Когда включается возмущение и с ним происходит перекачка энергии между модами, то возникают дополнительные спектральные моды в окрестности каждой моды с числом nj, j =0,3,6, которые перекрывают друг друга (рис. 9б). Малые изменения возмущения (AR = 1,7) приводят к резким изменениям формы спектра амплитуд вплоть до переключения знаков амплитуд Cm(k), как показано на рис. 9в.

Для того, чтобы расшифровать вырожденный спектр на рис. 9 б , требуется 3 ключа. Такими ключами являются спектры невырожденных пучков ЛГ (см. например, рис. 5) по аналогии с тем, как это делается в оптической спектроскопии при анализе спектров излучения источников света [41]. Особый интерес представляет измерение энтропии Шеннона сложного пучка с вырождением. В соответствии с формулой Шеннона (см. [39], стр. 8) энтропия сложного сигнала вычисляется как

MN

H m = ZE Ck n , k log 2 C m , n , k (bit),              (24)

n =0 k =0

где C m , _n , _k = p _n C 2n_n , _k являются перенормированными квадратами амплитуд C _m,_n,k , p _n = A 2,_n , есть вероятность обнаружить n -ю моду в исходном невозмущённом сложном пучке с вырождением. Другими словами, каждая k -я компонента в сумме (21) даёт вклад в n -й член в сумме (24) с вероятностью p n . Следовательно, имеет смысл сначала измерить энтропию сложного пучка, используя формулу (21), а затем сравнить её с энтропией (24), составленной из вторичных пучков ЛГ. Каждый модовый пучок в вырожденном спектре на рис. 9 вносит свой вклад в каждую линию сложного спектра, например,

С 3,0 = ^C 3,0,0 + ^C 3,3,0 + ^C 3,6,0 .

Используя спектры на рис. 5 а, б, в, находим C 3,0,0 * 0,9, C 3,3,0 * —0,05, C 3,6,0 * -0,22, откуда

C0 * 0,9-0,05-0,22 = 0,67, в то время как спектр на рис. 9б даёт Cз,о * 0,65, т.е. два альтернативных измерения отличаются в пределах ошибки измерений AC3,0 * 0,02.

Измерение меры неопределённости, введённой в сложный пучок возмущением, задаётся энтропией H m , зависимость которой от радиуса апертуры R приведена на рис. 9 г . Теоретическая кривая на рисунке иллюстрирует два режима динамики обмена энергией мод в вырожденном пучке. Быстрые осцилляции при малых радиусах апертуры сменяются монотонным стремлением энтропии к асимптотическому значению H _m * 1,584962501 после достижения радиусом критического значения R cr =4. В самом деле, когда радиус апертуры достигает своего критического значения, равного оптимальным размерам ЛГ-пучка R _n = V m + 2 n + 1, энтропия каждой моды достигает асимптотического значения H _m , _n ^- ( - 1/3log₂ 3 V2) и далее не изменяется. После того как радиус апертуры сравнивается с оптимальными размерами пятна ЛГ-моды R cr =4 с максимальным радиальным числом n = 6 изменение энтропии сложного пучка

H m .6 ^- 3 - ( - 1/3log3 ) * 1,584962501

прекращается.

а)

Рис. 10. Распределение интенсивности (инверсия) сложного пучка до сортировки (а); распределение интенсивности (инверсия) сложного пучка (б), сформированного рассортированными модами ЛГ с m = 3 и n 1 = 0, n 2 = 3, и n 3 = 6, R = 2. Степень корреляции изображений (а) и (б) составляет п = 0,92

б)

Экспериментальные точки на рис. 9 г следуют за теоретически предсказанным изменением энтропии с небольшими отклонениями. Довольно большая неопределённость, обозначенная энтропией сложного пучка, вносит ощутимую ошибку в измерительный процесс. Такие отклонения немедленно сказываются на процессе цифровой сортировки пучков. Реальным результатом сортировки являются два изображения сложных пучков на рис. 10.

Распределение интенсивности на рис. 10 а сформировано из трёх пучков ЛГ с различными радиальными числами на голографической решетке SLM-модулятора. Изображение на рис. 10 б является результатом цифровой сортировки мод этого пучка с последующим восстановлением также на SLM-модуляторе. Сравнение изображений даёт степень корреляции п* 0,92, которая едва превосходит критическое значение п cr * 0,9. Полученный результат, хотя и соответствует поставленным целям и задачам статьи, указывает на необходимость дальнейшего совершенствования метода цифровой сортировки пучков ЛГ для его практического использования.

Выводы

Таким образом, в результате проведённых исследований разработаны и воплощены основные принципы цифровой сортировки мод Лагерра–Гаусса по радиальному числу как в случае невырожденного, так и в случае вырожденного сложного пучка, подверженного возмущению в виде круглой апертуры переменного радиуса. Цифровая сортировка пучков ЛГ по ортогональному базису предполагает использование моментов интенсивности высших порядков и последующее сканирование соответствующих изображений модулированных пучков в фокальной плоскости сферической линзы. В результате получаем систему линейных уравнений относительно квадратов амплитуд и перекрёстных амплитуд мод возмущённого пучка. Решение системы уравнений задаёт массив квадратов амплитуд и перекрёстных амплитуд, которые позволяют определить амплитуды каждой моды ЛГ и восстановить как реальный массив пучков, так и сам комбинированный пучок в целом.

На эксперименте рассматривалось два типа пучков: простой пучок ЛГ и композиция простых пучков ЛГ с одинаковыми топологическими зарядами m (азимутальные числа) и различными радиальными числами n . Возмущение пучка осуществлялось посредством тонкой круглой диафрагмы с различными радиусами R отверстия. В результате возмущения возникало множество вторичных мод ЛГ с различными радиальными числами k , которое характеризовалось спектром амплитуд C m,n ( k ). Полученный спектр позволил восстановить как реальный массив мод ЛГ, так и сам возмущённый пучок со степенью корреляции не ниже η = 0,94. В качестве меры неопределённости, внесённой возмущением, измерялась информационная энтропия H m,n (энтропия Шеннона).

Возмущение сложного пучка приводило к возникновению вырожденного спектра амплитуд, когда одному радиальному числу k в спектре соответствует M возмущённых мод ЛГ с исходными радиальными числами n . Число вырождения равнялось числу исходных мод M . Для расшифровки и последующей сортировки вырожденного возмущённого числа потребовалось M ключей. В качестве таких ключей мы выбрали M спектров амплитуд C m,n ( k ) невырожденных возмущённых пучков при заданных радиусах R и начальных радиальных числах n . Измерения показали, что величина информационной энтропии существенно возрастала. Это сказалось на качестве сортировки реальных пучков, поскольку степень корреляции снизилась до η = 0,92, но не превышала критическую степень корреляции.

Рассмотренный новый метод цифровой сортировки пучков позволяет существенно упростить устройства сортировки пучков по радиальным числам, известные авторам, поскольку исключает из оптических устройств ряд интерферометрических элементов со сложным механическим и оптоэлектронным обеспечением. Вместо этого, измерения спектра пучка сводятся к сканированию распределения интенсивности и дальнейшей цифровой обработке массива данных с последующим восстановлением реальных пучков. Кроме того, использование вырожденных возмущённых пучков позволяет использовать новые распределения квантовых ключей в криптографии, в системах оптической связи и устройствах анализа рассеянного излучения от различных поверхностей.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-29-01233.