Сосредоточенная сила в однородной пористой среде

Большинство встречающихся в природе и используемых в науке и технике сред не являются однофазными и не могут быть отнесены к классу жидкостей, газов или твердых упруго деформируемых тел. Отличия в свойствах отдельных фаз, составляющих среду, и межфазные взаимодействия играют определяющую роль в динамике таких сред.

Теоретическое и экспериментальное исследования волновых процессов в упруго деформируемой пористой среде, насыщенной жидкостью или газом, являются актуальными и существенны для развития представлений о процессах, сопровождающих применение современных технологий использования пористых сред. К настоящему времени для теоретического исследования распространения волн в упруго деформируемой, пористой, насыщенной жидкостью среде имеется ряд подходов, из которых следует упомянуть теорию типа Френкеля-Био [1-3]. Данная математическая модель имеет ряд недостатков [4], и, кроме того, неясна возможность ее обобщения на случай конечных деформаций упругого скелета. В [5] отмечено, что произвольные изменения четырех параметров среды приводят к нефизичным результатам. Феноменологический подход, основанный на общих первых физических принципах, был использован при построении модели течения жидкости в упругой пористой среде для случая конечных деформаций [6]. Отметим, что система определяющих дифференциальных уравнений, построенных в [6], является гиперболической, однако привести все ее уравнения к симметрическому виду не удается. В [7] уравнения течения сжимаемой жидкости в упругой пористой среде выводятся с использованием метода термодинамически согласованных систем. Полученные дифференциальные уравнения

Работа выполнена при финансовой поддержке гранта Президента Российской Федерации „Ведущие научные школы“ НШ-5666.2014.5

образуют гиперболическую систему законов сохранения. Особенностью этих моделей является, наряду с распространением поперечной и продольной сейсмических волн, наличие второй продольной волны.

Данная работа посвящена получению решений линеаризованной системы уравнений пороупругости из [6] для простых сил. Отметим, что простейшие источники в пористых средах (модель Био) также рассматривались в [8-11] и в указанной в них литературе.

Пусть пространство R3 заполнено упруго деформируемой изотропной пористой средой. Распространения сейсмических волн в такой среде описываются следующей системой уравнений: линеаризованной системой динамических уравнений из [6]. Векторы скорости упругого скелета u и жидкости v удовлетворяют динамическим уравнениям для упругой и жидкой фаз в отсутствии диссипации энергии d2u — c2 Au + (c2 — a1) V V • u + a2 V V • v = F(t, x), dt2v + a3 V V • u — a4 V V • v = F(t, x),

где F = (F 1 ,F₂,F 3 ) — массовая сила, u = (u1,u₂,u₃), v = (v1,v₂,v₃), d t — частная производная по времени t, A, V и V^ - операторы Лапласа, градиента и дивергенции по x = (x 1 ,x₂,x₃) соответственно, коэффициенты a j, j = 1, 2, 3, 4 выражаются с одной стороны тремя упругими параметрами А, щ а = pa₃ + р2 и соответствующими парциальными плотностями упругой матрицы ps, жид кости p l формулами [6, 12]:

ai —----+ а ps,     a4 — a pi,     K — А + — щ, ps       p3

a 2 = ^p (K — ap ) ,    а з = K — ap s ,    p = p i + ps;

ρ ρsρ с другой стороны, тремя скоростями ct, cl. ,cl2 и соответствующими парциальными плотностями упругой матрицы ps, жид кости pl следующими формулами [13, 14]:

п _ pl  (22     2 Al 4 ps ai = J (cl. + cl2 + j ~ ct

■ z ^ρ

ρ

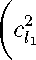
+ 2

-

2z —

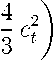
ρ s a 3 = — ^ρ

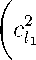
+ cl

-

2z —

ρ s a₄ = — ^ρ

+ cl

-

ρ s - ρ l z, ^ρ

p F = e f (t) ^( x - x o),

где e — единичнь :й вектор из R3, 5(x) — функция Дирака, f (t) — форма зондирующего сигнала по времени. Источники такого вида принято называть простой силой или сосредоточенной силой. Подставляя (3) в (1), (2) и переходя в полученных уравнениях к образам Фурье по времени, получим ш2 u — c2 VxVxu + а1 V V • u — а2 V V • v = —e — /(ш) 5(x — xo),         (4)

tρ ш2 v — аз VV • u + a4 VV • v = —e — f (ш) 6(x — xo),               (5)

ρ где Vx — оператор ротора no x, значок „крышка" означает преобразование Фурье по времени, ш — круговая частота.

Используя хорошо известную формулу векторного анализа e 8(x — xo) = — e- А^ = —   [VV • (e) -VxVx (e) i

4п R 4п       R /        V R и полагая u = Fo f (ш) V V • (Ui e) — VxVx(Ut e)J, v = Fo f (ш) VV-(vi e), из (4) и (5) получим

9 A1

ct Aut + ш ut =

4np R ш ui + ai Aui — a2 Avi =  -,

4np R ш v i — аз Aui + a4 Av i = --,

4npR где R = |R|. R = x — xo. c = Vц/ps.

Удобно ввести новые функции й^гч по формуле

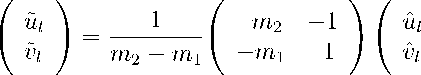
где mi = a3r- m2 = Дт a4-cl1            a4-cl2

Подставляя (11) в (9) и

(10), получим следующее уравнение

1 — 1/m2

c_h^Au i + ш u i =  ---------——,

• ¹              4np (1 — m 1 /m₂)R

• _{2        2}         1 — mi

• ^{C i} 2 ^A v ^{i +   1}   4np (m₂ — _mi)R.

  
  
  
  

Отметим, что при исчезновении пористости из (12), с учетом определения коэффициентов а₃, а₄, т 1, m 2 и определения скороетей продольных волн c _i1, c _{i 2}, получим уравнение для скалярного потенциала в упругой среде [15, 16].

Решениями уравнений (8)-(10), удовлетворяющих условиям щ(ш, 0) = 0, u_i(ш, 0) = 0, vi(w, 0) = 0, являются функции

-i kt R uMR) =  

4пш2рR ui(w,R) =

V l (ш,R)

1    1 - 1/m₂ 1 - e^-ik li ^R

4пш2р 1 — m1/m2R

1    1 — m 1 1 — e ^ik l2 ^R

4пш2р m2 — m1

где k n = n = t,l i ,l2.

c _n

Подставляя эти выражения в (6) и (7), получим

F 0 f (ш) e - ^ikt R__г (e ^ikt R e ik li R       e ^ik l2 R\ i

= ~A 2~ (    5 e ^{+ V V} "  e (   7,2 td     ^V 1 7,2 td     ^V 2   7,2 td )

4np q \ R           k \ч R       k 2 R       k t R ) a

A v =

F/ (ш)

0     ∇∇·

4пш2р

1              e i k l₁ R             e i k l₂ R

_R - m 1 ν 1   _{k t} 2 _R - m 2 ν 2   _{k t} 2 _R

⁶⁴ p i p s 4 c _t ⁴ .

9 p ²

где

1 — 1/m₂        1/m₂ — m 1 /m₂

1 — m 1 /m₂,   2      1 — m 1 /m 2

Формулы (14) и (15), используя единичную матрицу E = (5ij)3х3, можно представить в эквивалентном виде u = Fo /(ш)

4пш2р

_e - ik t R                      e - ik i1 R       e - ik i ₂ R

R )        ^     ^V 1    R ^{+ V} 2              e ,

A v=

F o /Н 4пш 2 р

w^ [E(l

R

- m 1 ν 1

e - i k l ₁ R k _t 2 R

- m 2 ν 2

]

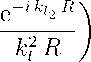
e .

Здесь 5 ij — символ Кронекера.

В этих формулах легко узнать, что выражения

G> ; x , x o ) = -Л_г- (VxVx ( E e-^ R ) — V V • 4пш²р X      \ R

E

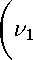
e - i k l ₁ R

R

+ V 2

_e - ik l₂ R

R

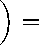
1           , e - ik t R           r_e - ik t R       _e - ik l1 R        _e -ikl ₂ R-,

4n^(1 + p l / p s ) \ R          _ k t R     ¹ k² R ² k² R

1                      1             e - i k l₁ R             e - i k l₂ R

G v^(ш; x , x ⁰’ = 4ПШ 2 Р ^{V V} • [^E (r ^{— m}1 ^V1Ц2Д -^— m^{2 V2} -iRR ) J =

1           /1            e - ik i1 R            e ~^ik i2 R\

= 4ПШ 2 Р^VV (r ^{— m}1¹¹RRT ^— m^2V2 "iRR-)

являются фундаментальной матрицей с компонентами Gu(ш; x, x₀), G v j.o (ш; x, x₀) (i0 = i + 3, j = j + 3, i, j = 1, 2, 3) системы уравнений пороупругости (9)-(ll), удовлетворяющей следующей системе дифференциальных уравнений:

ш2 Gu - c2 VxVxGu + ai W- Gu - a2 W • Gv = -p-1 E 5(x - xo), ш2 Gv - аз W • Gu + a4 W- Gv = -p-1 E 5(x - xo).

Тогда решения u и v через фундаментальные матрицы Gu и Gv выражаются согласно формулам u = Fo f(w) Gu e,    v = Fo f(w) Gv e.

Таким образом, получены решения системы уравнений пороупругости в частотной области для сосредоточенного источника. Показано, что при исчезновении пористости построенное решение переходит к решению системы уравнений линейной теории упругости в частотной области. Из построенных решений можно получить различные решения для разных сил в пористых, насыщенных жидкостью средах. Также из этих решений можно получить решения системы уравнений пороупругости во временной области.