Составление математической модели аксиально-поршневого гидромотора

во внедрении новых способов на основе инновационных технологий диагностики и анализа работоспособности гидроприводов. Для создания подобных устройств необходимо найти оптимальную запись математической модели гидропривода с возможными допустимыми упрощениями с одной стороны и с достаточным количеством параметров для ее более полного отображения с другой.

Цель работы: построение математической модели гидронасоса, позволяющей проводить исследование процесса работы гидростатической трансмиссии, как в штатных, так и в нештатных режимах работы, а также воспроизводить возможные дефекты и разрушения деталей гидропривода, что крайне важно при построении диагностической аппаратуры, основанной на методах неразборной диагностики и неразрушающего контроля.

Принцип работы гидростатической трансмиссии заключается в следующем: двигатель вращает вал насоса вместе с жестко соединенным с ним блоком цилиндров (рис. 1). Расположенный под углом к плоскости вращения обоймы опорный диск вызывает осевое перемещение опирающихся на него поршней. При этом рабочая жидкость из магистрали низкого давления попадает в полости, которые образуются в результате удаления поршней от распределительного диска. В процессе вращения блока цилиндров поршни начинают нагнетать жидкость в магистраль высокого давления. По ней жидкость попадает в рабочие камеры гидромотора, где ее давление передается на торцовые поверхности поршней, вызывая их перемещение в осевом направлении. Скользя по опорному диску, поршни устремляют за собой блок цилиндров, который жестко связан с выходным валом. Таким образом, на валу формируется крутящий момент. Пройдя рабочие камеры гидромотора, рабочая жидкость вновь возвращается в магистраль низкого давления. Расчетная схема гидромотора представлена на рис. 2.

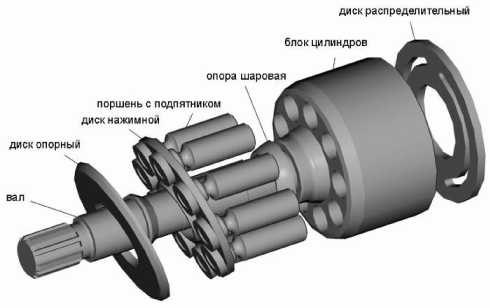
Рис. 1. Основные детали аксиальнопоршневого гидромотора и гидронасоса

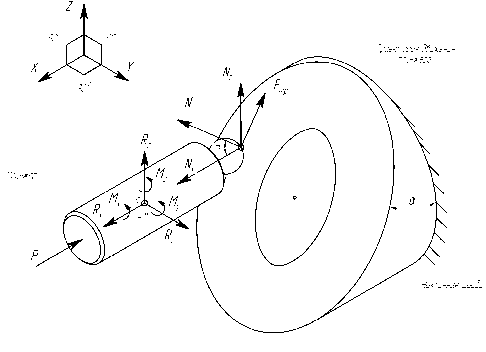
Рис. 2. Расчетная схема аксиальнопоршневого гидромотора

С одной стороны плунжер опирается на неподвижную наклонную шайбу, с другой на него действует сила Р, создаваемая давлением рабочей жидкости, которая поступает из магистрали высокого давления. В точке контакта плунжера и наклонной шайбы возникают 2 силы: нормальная сила реакции N, направленная перпендикулярно наклонной шайбе, и сила трения Fтр, которая является силой граничного трения, то есть представляет собой совокупность сил сухого и вязкого трения. Соотношение и величина составляющих сил трения зависит от степени износа наклонной шайбы, подпятника, плунжерной пары, качества рабочей жидкости, режима работы и т.д.

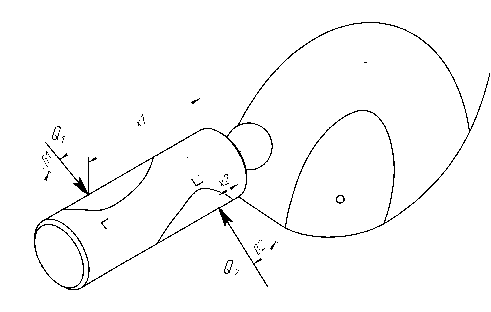
Рис. 3. Представление пространственной распределенной нагрузки

Контакт плунжера и обоймы создает две пространственно распределенных нагрузки q 1 и q ₂, которые можно заменить двумя равнодействующими силами Q 1 и Q ₂ (рис. 3), проходящими через ось поршня перпендикулярно ей под углами в 1 ^и А к плоскости xy и приложенными на расстоянии x 1 и x ₂ от точки контакта плунжера с наклонной шайбой. В этих точках также возникают силы трения F _тр1 и F _Tp2, направленные по касательной к поверхности плунжера. Приведем систему сил, действующих на плунжер со стороны обоймы, к главному вектору R и главному моменту M , приложенным в центре масс плунжера.

Запишем уравнения движения поршня в абсолютной системе координат:

mx = - P - R_x + N cos a - F_ooo ;

my = R y ^- F o ;

mz = R_z + N sin a - F_ooz ;

J_xv x = M x ;

J_y ф_y = - Pr cos( ^ ) + R_xr cos( ^ ) - R_zx_c - N cos a • r cos( ^ ) + ^{+ N sin a} • ^xN ^- F_dd3 ^{r cos(} ^ ) - F_dd z • ^xN + M y ;

J _z& _z = - Prsin( ^ ) + R_xr sin( ^ ) + R_yx_c + N cos a- r sin( ^ ) - ^{- F}odo ^{r sin(} T ) ^{+ F}oy • x N ^{+ M}z .

где Rx, Ry, Rz, Mx, My, Mz - соответствующие проекции главного вектора и главного момента на координатные оси, ф - угол поворота обоймы, x_c, x_N - координаты центра масс плунжера и точки контакта с наклонной шайбой, P - сила, создаваемая давлением жидкости, ^Fddx , ^Fddy , ^Fddz - соответствующие проекции силы трения на оси координат, которые выражаются следующим образом:

fN cos( F o₆ ; x ) sign (;&),| x | >  0;

F oox

= p x + i fN ^{cos( F} o_d ; ^x ) sign ( £ ^F x X ^x = 0, £ ^F x | >  fN ^{cos( F} o6 ; ^x );

£ ^F x , ^x = ⁰, £ ^F x | <  fN ^{cos( F} o6 ; ^x X

fN ^{cos( F} oo ; y ) sign ^{( y} XI ^y | > 0;

F ooy

= p y + \ ^{fN cos(F} 66 ; y ) sign ⁽ £ ^F y X ^y = ⁰, £ ^F y I >  fN ^{cos( F} 66 ; y );

£ ^F y , ^y = ⁰, £ ^F y I <  fN cos^{( F} 6 ₆ ; y X

fN cos( F oo ; z ) sign ( j&), | z\ >  0;

^F o6z = p z ^{+ <}

fN ^{cos( F} oa ; ^z ) sign ⁽ £ ^F z X ^z = ⁰, £ ^F z I >  fN ^{cos( F} oa ; ^z );

_ £ ^F z , ^z = ⁰, £ ^F z I <  fN ^{cos( F} oa ; ^z x

где J - коэффициент сухого трения.

В представленных выражениях составляющие M x , R y , M z описывают вязкое трение, пропорциональное скорости движения плунжера относительно неподвижной шайбы, в проекциях на координатные оси. Второе слагаемое описывает силу сухого кулоновского трения. Для определения углов между вектором силы трения и осями координат учтем, что линия действия этой силы совпадает со скоростью плунжера в точке контакта, а, следовательно, соответствующие углы могут быть определены следующим образом:

& cos(Foo ,x) = , 2 x2    2 ;

y )C + y + z

cos( F oo , у ) =

cos( F_oo , x ) =

у

2    -2    -2 ;

x + y + z

z

7 x & ² + y ² + z ²

Так как в уравнениях движения присутствует угол поворота обоймы, запишем уравнение вращения обоймы при условии, что на нее действует сила только со стороны одного плунжера:

J

y = r sin( ф );

y = r еos( ф ) • ф ;

y = r ( - sin( ф ) • ф ² + cos ^ ) • ф );

z = r еos( ф );

z = - r sin( ф ) • ф ;

z = - r (еos( ф ) • ф ² + sin( ф ) • ф ).

При условии безотрывного движения плунжера по поверхности шайбы координата x также может быть выражена через угол φ следующим образом:

z = ax + b = x • tg (90 + а ) + x ₀;

x = x 0 tg( а ) - z • tg( а );

.x = r • tg ( а ) • sin( ф ) • ф ;

x = r • tg( а ) • (еод( ф ) • ф ² + sin( ф ) • ф ).

Выводы: уравнения (1) и (4) с учетом выражений (2), (5) и (6) описывают работу аксиально-поршневой группы гидронасоса. Исследуя поведение системы при различных параметрах, в частности, при различных соотношениях составляющих вязкого и сухого трения между подпятником плунжера и наклонной шайбой и между плунжером и обоймой, можно выявить диагностические признаки, позволяющие определять дефекты методами неразрушающего контроля, такими как измерение вибрации корпуса, давления рабочей жидкости в магистралях и т. д.