Состояние и продуктивность водных экосистем. Математическое моделирование

Рассмотрим изменение биологических компонентов системы фитопланктон–биогены–свет с глубиной в стационарном режиме. Условие стационарности режима в системе уравнений в частных производных с диффузией приводит к следующей модели:

fd²P 1

-^=-Ve(P)-p(C,I,Ty\P dz^ к d2C у

^ = -W.i.n-MPW

V_Tz = -«(P.c)i .

Распределение объемной плотности P (t, z) биомассы фитопланктона по глубине z зависит от распределения концентрации C (t, z) массы минеральных питательных веществ (биогенов), освещенности (в частности, фотосинтетически активной радиации – PAR) I (t, z) и температуры T (t, z). Процесс происходит в течение времени t ∈ [0, tm] и по глубине z ∈ [0, zm]. Функция удельной скорости роста µ (C, I, T) основана на гипотезе независимо- сти выделенных влияющих факторов и выражается в видец(.с,1,т^ — Ho" HcQQ'i^iUV ИтСО, где µ0 – максимально возможная скорость роста фитопланктона, μс(С) – зависимость скорости роста от биогенов, соответственно μI(I) – от освещенности, μT(T) – от температуры. Для динамики биогенов важно, какую долю составляют учтенные минеральные вещества в растительных организмах – параметр γ, а также какова скорость возврата их в систему после бактериального разложения – параметр β, α (y, z) – удельная скорость ослабления освещенности. Здесь имеется краевая задача для z∈[0,zm], где zm – глубина фотического слоя. Данные дистанционного зондирования, характеризующие хлорофилл, температуру и облучение в поверхностном слое, могут быть использованы в качестве левого граничного условия (z = 0). Системное решение требует информации о количестве биогенов или растительного пигмента на дне или на нижней границе фотического слоя zm.

Следующая модель отображает подобный процесс посредством решения задачи Коши с использованием концепции адаптации [2, 3]:

rdP    du

"T=V1"P dz    dz dC

U = wf(P)C dz di где ν – определенная максимально возможная скорость роста сообщества. Функция f(P) основана на гипотезе об обратном влиянии фитопланктона на плотность минерального питания [4].

Модели, проверенные на основе данных in situ , показывают адекватное отображение динамики интегрированной биомассы в зависимости от внешних условий. Комплексное использование спутников и информации in situ дает возможность с хорошей точностью получать оценки численности фитопланктона на большой территории. Для сравнения распределений фитопланктона в теплый 2015 г. и холодный 2016 г. используется модель с функцией адаптации. Сравнение теплых и холодных лет на шельфе Западной Камчатки показывает динамику видового состава в зависимости от типа года. Основной вывод, содержащийся в литературных источниках [1], заключается в том, что видовой состав региона стабилен в многолетней динамике. Меняются только соотношения. Набор доминирующих видов изменяется в зависимости от условий окружающей среды. По объемам размножения видов при определенных температурных условиях можно сделать вывод,

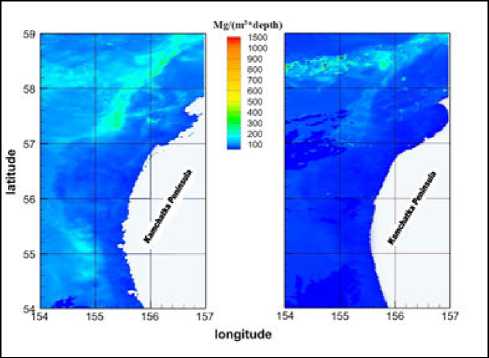
что структура доминирующих видов соответствует температурному режиму. Этот факт учитывает результаты модели в теплые и холодные годы. Видовой состав изменяется для лучшей приспособляемости сообщества фитопланктона к условиям окружающей среды.