Совершенствование методик расчета динамических параметров упругих элементов УДО роторов ГТД

При радиальном нагружении такого упругого элемента предполагалось, что ось подшипника перемещается в пространстве, сохраняя свое первоначальное направление, благодаря чему исключаются перекосы колец подшипника [1]. Однако это выполняется не при всех соотношениях геометрических параметров упругой втулки. Более обоснованные результаты можно получить, если использовать усовершенствованные методики расчета, основанные на методе конечных элементов. Для расчетов воспользуемся профессиональным комплексом конечно-элементного анализа конструкций ANSYS 5.5. Метод конечных элементов (МКЭ) позволяет рассчитывать упругие элементы любой конфигурации. Для получения приемлемой по точности расчета МКЭ модели, путем оптимизации элементной сетки, необходимо результаты расчета сравнивать с экспериментальными значениями жесткости упругой втулки.

В качестве исследуемого объекта в статье рас-

Рис. 1. Упругий элемент типа “беличье колесо”

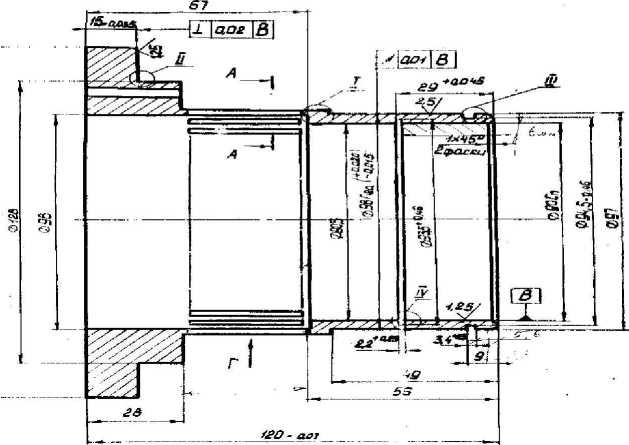
Рис. 2. Схема упругого элемента типа “беличье колесо” с геометрическими параметрами:

/, =34,2 мм - длина, /2 = 1,73 мм - толщина, 6=2,7мм - ширина упругих балочек соответственно; и=40 - число пазов; 1₀ = 120 мм - общая длина упругой втулки

сматривается упругий элемент типа “беличьего колеса” экспериментальной установки для исследований динамики ротора на опорах с ГДД [3], разработанной в СГАУ. Схема упругой втулки и обозначения приведены на рис. 2.

Жесткость такой упругой втулки определялась опытным путем [3]. На рис. 3 представлена схема измерения жесткости упругих элементов типа “беличьих колес”. Для экспериментального определения жесткости упругая втулка 2 устанавливается на стол 1 и с помощью механических прижимов закрепляется на столе. С одной стороны монтируется динамометр 4, через который с помощью винтового механизма прикладывается сила, фиксируемая индикатором 3. С противоположной стороны устанавливаются два индикатора часового типа 5 и 6, по показаниям которых определяется перемещение втулки под действием фиксированной силы. После статистической обработки экспериментальных данных вычислялись значения коэффициента жесткости упругой втулки. Разность показаний индикаторов 5 и 6 обозначает перекос рабочей поверх

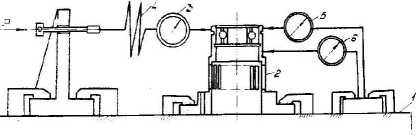
Рис. 3. Схема замера жесткости упругих элементов типа “беличьих колес”

ности упругой втулки, то есть отклонение ее от вертикальной оси.

На рис. 4 представлена конечно-элементная модель упругой втулки типа “беличьего колеса”, выполненная на основании данных рис. 2. При составлении конечно-элементной модели использован объемный конечный элемент типа “solid 45” оптимизированной формы (рис. 5).

В результате расчета при нагрузке втулки сосредоточенной силой 1 кН было получено в диаметрально противоположной точке перемещение величиной 188 мкм. В сравнении со среднестатистическими экспериментальными данными (при нагрузке в 1 кН среднее значение перемещения равнялось 200 мкм) погрешность составляет 6 %. Несоответствие рассчитанного значения перемещению в опыте объясняется погрешностью эксперимента и технологическими

Рис. 4. Геометрическая модель упругого элемента типа “беличьего колеса”

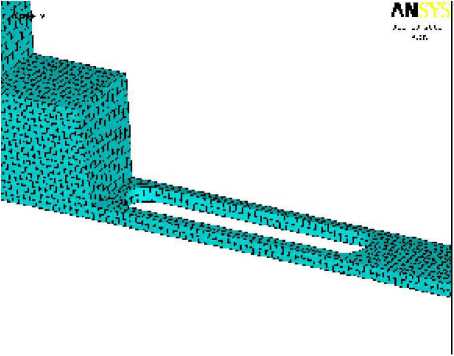
Рис. 5. Разбиение сектора упругого элемента при оптимальной форме конечных элементов отклонениями размеров реального упругого элемента от теоретической модели. Для уменьшения времени расчета, которое при использовании компьютера на базе процессора “Athlon 700” составило 23 часа, необходимо было оптимизировать конечно-элементную модель. С этой целью число разбиений объемов втулки справа и слева от упругих балочек уменьшено в десять раз, как показано на рис. 6.

Для оптимизированной модели было получено значение перемещения в рассматриваемой точке равное 185 мкм, что отличается от результата для исходной модели всего на 1,5 %, при этом время расчета сократилось до 1 часа.

Проанализировав конструкцию упругой втулки, можно предположить, что массивная фланцевая часть практически не деформируется и при составлении расчетной модели ее можно отбросить (рис. 7). Расчет, произведенный для теоретической модели без фланцевой части показал, что перемещение в рассматриваемой точке уменьшилось до 183 мкм, отличие от результата для оптимизированной модели менее 1 %, a для исходной модели 2,7 %, причем время расчета сократилось до 20 минут.

Рис. 6. Схема оптимизированного разбиения упругого элемента

Рис. 7. Усеченная конечно-элементная модель упругой втулки

На рис. 8 представлена деформационная картина упругого элемента типа “беличьего колеса”. Для определения величины перекоса на конце упругой втулки из области максимальной деформации был выделен фрагмент в виде сектора (рис. 9).

Из рис. 9 следует, что упругая втулка испытывает деформацию изгиба, а напряженное состояние, в основном, определяется напряжениями в упругих балочках. Причем максимальная величина напряжений согласно прочностным расчетам составила 450 МПа, что вдвое ниже предела прочности материала упругой втулки, изготовленной из стали 65Г.

Кроме того, из рис. 9 видно, что на конце втулки деформации больше, чем в районе упругих балочек. Таким образом, имеет место перекос цилиндрической поверхности, который в рассматриваемом случае составляет 5...6 мкм. Согласно экспериментальным данным перекосы на конце исследуемой упругой втулки не превышали 5 мкм. Следовательно, для ГДД с демпферным зазором величиной <7=0,1 мм его перекос составляет всего 5...6 %. Однако величина перекоса на конце упругой втулки зависит от геометрических параметров балочек. Конструкция упругого элемента типа “беличьего колеса”, спро-

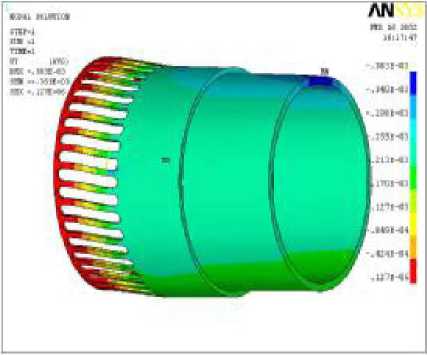
Рис. 8. Вертикальные перемещения в упругом элементе

Рис. 9. Вертикальные перемещения фрагмента упругого элемента ектированная для опоры перспективного двигателя НК-126 [4] со следующими геометрическими параметрами: L =33 мм; //=2 мм; 6=2,7 мм; /7=40; L = 56 мм, в случае приложения радиальной нагрузки, равной 800 Н, имеет расчетный! перекос цилиндрической части уже 15 мкм, что составляет 15 % от величины демпферного зазора d ,=0,1 мм. В динамике с увеличением нагрузки перекос увеличивается и может достигать 30 % от величины демпферного зазора.

Жесткость упругой втулки характеризуется коэффициентом жесткости c=F/y, (3)

где F сила нагружения; у - перемещение упругой втулки, замеренное в точке, противоположной точке приложения силы.

Для исследуемой конструкции упругого элемента (рис. 2) экспериментально полученный коэффициент жесткости имеет среднее значение

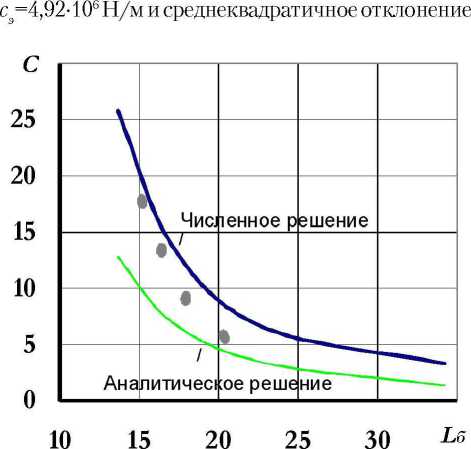
Рис. 10. Зависимость безразмерного коэффициента жесткости Сот безразмерной длины упругих балочек L₆

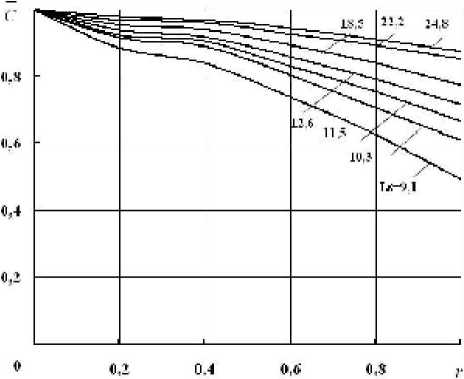
Рис. 11. График зависимости относительной жесткости С от относительного радиуса f при различных L₆

s =±0,34-10⁶Н/м. Согласно результатам численных расчетов перемещений исследуемой упругой втулки получаем из уравнения (3) значения коэффициента жесткости с=5,32...5,46-10⁶Н/м, что хорошо согласуется с экспериментальными данными. Расчет для аналогичного упругого элемента по аналитической зависимости (1) с учетом поправочного коэффициента /у дает заниженное значение коэффициента жесткости с=2,8-10⁶Н/ м. Таким образом, отличие аналитического значения коэффициента жесткости от экспериментального составляет более 40 %. На основании проведенных исследований можно сделать вывод, что метод конечных элементов дает более достоверные результаты, чем аналитический расчет. Кроме того метод позволяет получать картину распределения напряжений и деформаций в упругой втулке, что особенно важно для определе-

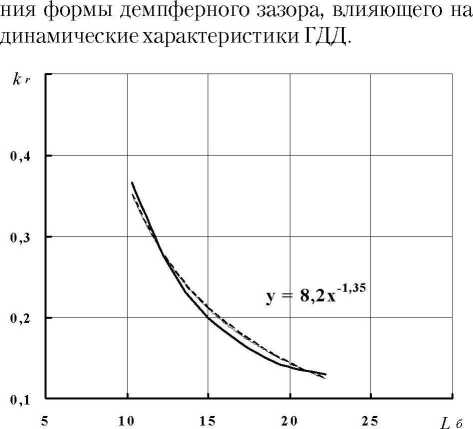
Рис. 12. Зависимость коэффициента к от безразмерной длины упругих балочек L_&

С целью обобщения полученных результатов исследований и распространения их на весь класс таких упругих элементов рассмотрим зависимости безразмерного коэффициента жесткости C _ ch] F от безразмерной длины упругих балочек L₆ = 1б /h (рис. 10) для случаев аналитического расчета – по зависимости (1) с учетом равенства (2), численного – по предложенной методике. С целью изменения жесткости опытного образца упругого элемента внутрь по переходной посадке устанавливалась толстостенная втулка. Экспериментальная зависимость значений коэффициента жесткости от относительной длины упругих балочек достигалась изменением положения дополнительной втулки в осевом направлении.

Из графиков рис. 10 видно, что с изменением длины прорезей жесткость упругого элемента изменяется. Экспериментальные значения существенно превышают аналитические данные, что объясняется принятыми допущениями в теоретической модели аналитического расчета. В частности, упругие элементы типа “беличьих колес” имеют аксиальные пазы не строго прямоугольной формы, а со скруглениями углов радиусом r , что обусловлено требованиями снижения концентрации напряжения. В связи с этим необходимо оценить влияние величины радиуса скругления на жёсткостные характеристики упругого элемента. Исследуем влияние безразмерного радиуса скругления пазов r = r/b на относительную жёсткость упругого элемента С _ с 0 / с , где с0 и с - коэффициенты жесткости, определяемые методом конечных элементов для нулевого и заданного радиуса скругления соответственно.

Из анализа графика на рис. 11 видно, что не-учёт радиуса скругления r пазов в расчете жесткости упругого элемента типа “беличьего колеса” может дать погрешность в определении коэффициента жесткости до 50 %. Анализ конструкций УДО роторов ГТД показал, что значения безразмерной длины упругих балочек лежат в диапазоне L6 = 10...25 . Уравнение для параметра относительной жёсткости С , учитывающего влияние радиуса скругления упругих балочек имеет следующий вид:

С _ 1 - krr .

Зависимость коэффициента k_r от L_б можно аппроксимировать степенной функцией вида у = ахт (рис. 12).

Тогда относительная жёсткость упругого элемента может быть аппроксимирована зависимостью С = 1 - 8,2 L-³⁵r .

Максимальная погрешность аппроксимации составила не более 8 %.

Выражение для жёсткости с учётом радиуса скругления примет вид

_ nEbh ( b ² + h ²) _k c = 2 P₆ (1 - 8,2 L-'■" r ) '•

Таким образом, получено аналитическое выражение для определения жёсткости упругого элемента типа “беличье колесо”, учитывающее величину радиуса скругления прорезных пазов. Данная зависимость существенно повышает точность определения жёсткостной характеристики.