Совершенствование методов измерения параметров сигналов для систем контроля и испытаний радиоэлектронной аппаратуры

и обеспечивающий повышение точности измерения ПГС за счет исключения данного вида погрешности. Кроме того, реализация метода сокращает общее время определения параметров, поскольку позволяет начинать процесс измерения в произвольный момент времени.

Метод измерения параметров с временным разделением мгновенных значений сигналов заключается в том, что на вход системы и на контролируемый усилительный тракт РЭА подают гармонический сигнал; в произвольный момент времени одновременно измеряют мгновенные значения входного напряжения и выходного напряжения, поступающего с выхода усилительного тракта; через образцовый интервал времени Δ t одновременно измеряют мгновенные значения входного и выходного напряжений; через такой же интервал времени снова одновременно измеряют мгновенные значения входного и выходного сигналов. Частоту, амплитудные значения входного и выходного сигналов, а также угол сдвига фаз между ними определяют по измеренным значениям. Временные диаграммы, поясняющие метод, представлены на рис. 1.

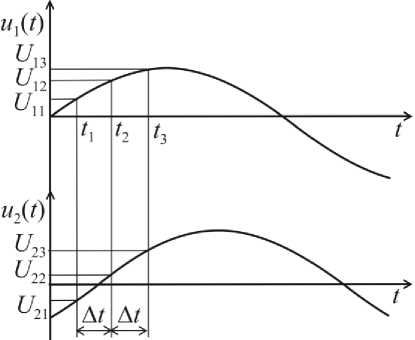
Рис. 1. Временные диаграммы, поясняющие метод

Входное напряжение и напряжение на выходе РЭА, имеющие гармонические модели, соответствуют следующим выражениям:

u1 (t) = Um 1 sin гоt; u2 (t) = Um2 sin(rot + ф), где U и U - амплитудные значения входного напряжения и выходного напряжения усилительного тракта; ω - угловая частота входного сигнала; φ - угол сдвига фаз между выходным и входным сигналами усилительного тракта.

В произвольный момент времени t 1 мгновенные значения сигналов на входе и выходе РЭА примут вид:

U11 = UmIsin «1 ; U21 = Um2 sin a2 , где α1 и α2 – начальные фазы сигналов в момент времени t1.

Через образцовый интервал времени Δ t (в момент времени t 2 ) мгновенные значения напряжений будут соответствовать:

U12 = Umi sin(a1 + mA t);

U2 2 = Um 2 sin(a2 + mAt).

Через интервал времени Δ t (в момент времени t 3 ) мгновенные значения сигналов будут равны:

U13 = Um1 sin(a1 + 2mA t);

U23 = Um2 sin(a2 + 2mAt).

Используя мгновенные значения сигналов, после преобразований можно получить следующие выражения:

cosa - 2 U 122 — U 13 U 11 — U и ;	(1)
cos Laj             < 2 U 12 V U 122 — U 13 U 11
( 2 U 22 — U13U ,,— U 2, ) 2 . sin a, = 1 —      12, / " 11 -----11    ; 1   \      4U 122 ( U 122 — U 13 U 11 )	(2)
cos a = 2U 222 — U 23 U 21 — U 221 ;	(3)
" 2    2 U 2 2 4U 222 — U 2 3 U 21
( 2 U 22 — U23U 2, — U 22, ) 2 . sin a, = 1 —      22    23 21    21    ; 2    \     4U 222 ( U 22 — U 23 U 21 )	(4)
cos mA t = U 13 + U 11 .	(5)

2 U 12

Из выражений (2) и (4) можно определить ам- плитудные значения сигналов на входе и выходе усилительного тракта РЭА:

временного интервала Δ t . Анализ (1) - (5) показывает, что знаменатели данных выражений обращаются в ноль или принимают некорректные значения, если U 12 = U m 1 sin ( a ₁ + mA t ) =0 и (или) U ₂₂= U„ ₂sin ( a₂+mA t ) =0 • Для того, чтобы устранить возможность деления на ноль, необходимо проводить анализ мгновенных значений U 12 и U 22 и, если хотя бы одно из них равно нулю, следует измерять четвертые мгновенные значения напряжений U 14 и U 24 через временной интервал Δ t' =2Δ t=t 4 - t 3 (рис. 2). Если, например, U 12 =0, а U 22 ≠0, то выражения (1), (2) и (5) преобразуются к виду:

cos a,

2 U 1²з — u 1 U 11 — u 2 ; 2 U 13 7 U 1²3 — U 1 U 11

sin aj =

1 1   ⁽ 2 ^U 23 ^{— U} 14 ^U 11 ^{— U} ;

V    4U23(U123 — U^UJ cos mAt =

U 14 + U 11 2 U 13

Выражения (3) и (4) остаются без изменения.

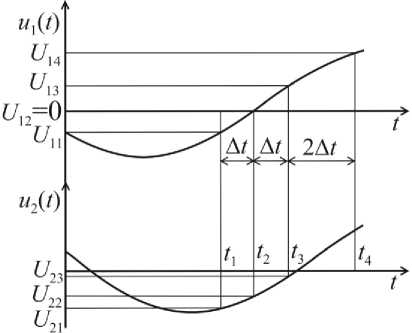
Рис. 2. Временные диаграммы при U 12 =0 и U 22 ≠0

Из выражений (6) и (7) следует, что для того, чтобы устранить некорректные результаты, необходимо проводить анализ мгновенных значений U 11 и U 21 и, если хотя бы одно из них равно нулю, следует измерять четвертые мгновенные значения напряжений U 14 и U 24 через временной интервал a t = t ₄ — 1 ₃ (рис. 3).

U

m 1

^U 11   ;

sin a]

U

U21 m 2       • sin a2

Из выражения (5) следует, что частота входного

сигнала равна:

f

=----- arccos

2 nA t

Г u 13 + u11J

I 2 U 12 ^J

Угол сдвига фаз между выходным и входным сигналами ф можно определить, используя выражения (1) и (3)

ф = a2 — aj = arccos (cos a2) — arccos (cos a,).       (9)

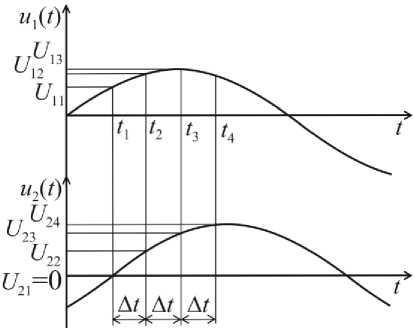
Рис. 3. Временные диаграммы при U 21 =0 и U 11 ≠0

В рассматриваемом методе время измерения не зависит от момента начала измерения, угла сдвига фаз между входным и выходным напряжениями и периода сигнала, а определяется в основном длительностью

Если, например, U 21 =0, а U 11 ≠0, то выражения (3), (4) и (7) преобразуются к виду:

sin a₂ =

= 2U 223 - U ₂₄ U ₂₂ - U 222 ;

2 U 2 3 7 U 223 - U 2 4 U 2 2

/i  ⁽ 2 ^U 23   ^U 24 ^U 22   ^U 22 У ;

1 ^;

V     4 U 23 ^ 0 223 - U 24 U 22 )

^U 22

Um 2     -  _ sin a2

V.» =^П ( 2 q + 1 ) - k a₂, ^где h uk U km ^- коэффициент ^{k -той} гармонической составляющей напряжения; q = 0; 1. Предельное значение абсолютной погрешности определения амплитуды сигнала в соответствии с (4) и (7) будет равно

Выражения (1), (2) и (5) остаются без изменения. Схема системы контроля и испытаний РЭА, реализующей данный метод, представлена на рис. 4. В состав системы входят: генератор синусоидального напряжения ГСН, первичные преобразователи напряжения ППН1 и ППН2, аналого-цифровые преобразователи АЦП1 и АЦП2, контроллер КНТ, шины управления ШУ и данных ШД .

A U m 2 =

d U m 2 d U 21

+

еи, m2

s U 22

+

d U.

5 U 23

m 2

max

.

Частные производные в выражении (12) с учетом (4), (7) и (11) приводятся к следующему виду:

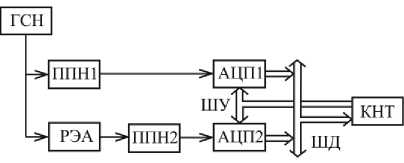
Рис. 4. Схема системы, реализующей метод

d U_m2 _ ctga₂   ctga₂ sin ( a₂ + 2 roA t )

d U21   2 sin roAt L       sin roAt sin(a2 + 2roA t) + 2 sin a2      1

sin a₂ sin(a₂ + roA t )      sin a₂

Рассматриваемый метод предназначен для определения параметров гармонических сигналов. Если усилительный тракт РЭА вносит нелинейные искажения, то при гармоническом входном сигнале неизбежно возникает погрешность, обусловленная наличием высших гармоник. При этом амплитудное значение и частота входного сигнала в соответствии с выражениями (6) и (8) определяются без методической погрешности.

Анализ погрешности метода из-за отклонения реального сигнала от гармонической модели. Проведем оценку погрешности, обусловленной отклонением реального сигнала от гармонической модели, используя методику оценки погрешности результата измерения параметра как функции, аргументы которой заданы приближенно с погрешностью, соответствующей отклонению реального сигнала от модели [5]. Пусть предельные абсолютные погрешности аргументов соответствуют наибольшему отклонению моделей от реальных сигналов

d U_{m 2} _ ctg a ₂     2 ___ cos a ₂

d U₂₂ “ sin a₂ L sin roA t  sin(a₂ + roA t )

cos a2 sin(a2 + roAt)

sin2 roAt_ dUm2 =      '

5 U23   2 sin a2 sin roAt cos a21

x -—77 —T-—:—— .

sin roA t  sin( a₂+roA t )

В общем случае относительная погрешность измерения амплитуды выходного напряжения будет равна

5 u

to

T huk k =2

d U m 2 3 U 21

+

SU , m 2

+

5 U m 2

3 U 23

^{A U} max = ^SuP

to

TU^ sin(ku + ka + k=1

- U 1 _m sin ( u / + a 2 )

где ^ i uk — угол сдвига фазы k-той гармоники напряжения относительно первой; и_ы - амплитудное значение k -той гармонической составляющей выходного напряжения; U - амплитуда первой гармонии выходного напряжения.

Если параметры первой гармоники реального сигнала совпадают с параметрами сигнала, соответствующего гармонической модели, то (10) примет вид

to

' 1+T huk k=2

а и ₂₂

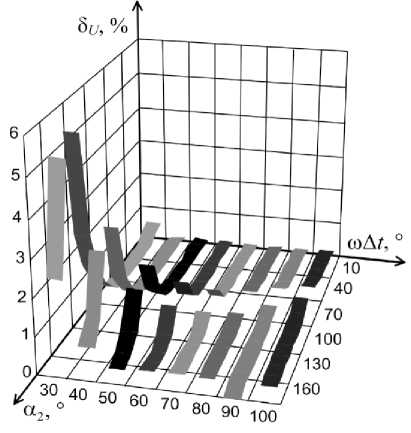
Рис. 5. Графики зависимости погрешности 5 и от a 2 и и Д t

to

A U „о.

= suP ^U 1 m £ h uk ^si n ( ^k » t ^{+ k} « 2 ⁺ V 1 uk ) ’

k = 2

Выражение (11) принимает максимальное зна-to чение U1 m Thuk, если |sin(krot + ka2 + Vi„t) = 1, т.е. при

На рис. 5 представлены графики зависимости погрешности 5 и от начальной фазы сигнала а 2 и и Д t в соответствии с (13) при наличии в сигнале 1-й и 3-й гармоник для h _u 3 = 0,1% .

Если абсолютные погрешности аргументов соответствуют наибольшему отклонению модели от реального сигнала, то предельное значение абсолют-

ной погрешности определения угла сдвига фазы между сигналами на входе и выходе РЭА в соответствии с (3) и (9) примет вид:

Аф =

дф    дф

U д Ц ;

дф д Ц 3

А U max

.

Частные производные в выражении (14) с учетом (3), (9) и (11) приводятся к следующему виду:

дф    0,5 [ sin2 гoA t - sin ( 2a₂ + 2 гоА t )]

д U21               sin гоА t sin a7         ;

+-- sin гоА t sin(a2 + гоА t)

дф       4       2 cos a₂

--- —---- д U22   sin гоА t  sin(a2+гoA t)

2cos a₂ sin(a₂ + гоА t )   ;

sin2 гоА t       _ дф _ sin2 a2 cos(a2 + гоАt)

д U₂₃    sin(a₂ + гоА t ) sin² гоА t

В общем случае приведенная погрешность измерения фазы между входным и выходным напряжениями будет равна

oo

У ф

Z hu_k — k = 2

^дф ₊ ф д U ₂₁    д U ₂₂

д U ₂₃

На рис. 6 представлены графики зависимости погрешности γ_φ от начальной фазы сигнала α 2 и ω Δ t в соответствии с (15) при наличии в сигнале 1-й и 3-й гармоник для h u з = 0,1% .

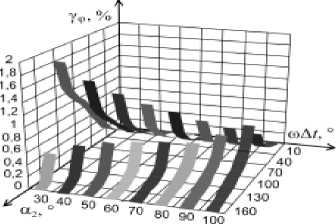
Рис. 6. Графики зависимости погрешности γ_φ от α 2 и ω Δ t

Анализ рис. 5 и 6 показывает, что при увеличении образцового интервала времени Δ t по сравнению с периодом сигнала погрешности измерения амплитуды

и угла сдвига фазы снижаются и достигают минимальных значений при m A t =90 ° , однако это приводит к возрастанию общего времени измерения. При дальнейшем увеличении угла сдвига ω Δ t погрешности снова возрастают. Разрывы графиков обусловлены значениями начальной фазы α 2 и ω Δ t , при которых знаменатели в соответствующих выражениях обращаются в ноль.

Выводы: разработанный метод определения параметров гармонических сигналов не использует дополнительные сигналы, что позволяет повысить точность измерения. В рассматриваемом методе время измерения не зависит от момента начала измерения, угла сдвига фаз между входным и выходным напряжениями и периода сигнала, а определяется в основном длительностью временного интервала Δ t . Проведенный анализ показывает, что наличие в сигналах высших гармоник приводит к существенному увеличению погрешности измерения ПГС. Полученные результаты позволяют подбирать оптимальное соотношение между образцовым интервалом времени Δ t и периодом сигнала исходя из требований по точности и времени измерения.

Работа выполнена при финансовой поддержке РФФИ (грант № 16-08-00252 А)