Совершенствование методов расчета электромеханического привода с учетом переменности нагружения
Автор: Ивановская Александра Витальевна, Богатырева Елена Владимировна
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 1-2 т.18, 2016 года.
Бесплатный доступ
В работе рассмотрена проблема описания нестационарных процессов отдельного класса электромеханических систем на примере неводовыборочного комплекса. В результате исследований была решена задача совершенствования методов расчета электромеханического привода с учетом переменности нагружения. Полученные аналитические зависимости для определения силы натяжения стяжного троса могут быть использованы на этапе проектирования ЭМП промысловых лебедок. Также результаты исследования, изложенные в данной работе, на этапе проектирования могут обеспечить повышение эксплуатационной надежности и эффективности работы системы привода на основе выбора рациональных параметров эксплуатации.
Электромеханический привод, математическая модель, промысловая лебедка, переменность нагружения, неводовыборочный комплекс, кошельковый невод, стяжной трос
Короткий адрес: https://sciup.org/148204367
IDR: 148204367 | УДК: 62-192
Текст научной статьи Совершенствование методов расчета электромеханического привода с учетом переменности нагружения
Очевидно, что главная задача агропромышленного комплекса – это обеспечение продовольственной независимости нашего государства. Для решения этой задачи важным направлением является добыча гидробионтов. В частности, лов рыбы требует высокого уровня механизации и автоматизации всех этапов технологического процесса. Все промысловое оборудование в процессе своей работы испытывает значительные динамические нагрузки, и, как следствие, имеет место большое число отказов в работе данного оборудования. Значимость данной проблемы привлекло к ее решению большое количество инженеров и ученых [14]. На сегодняшний день существующие методики расчета параметров работы данного класса механических систем хорошо апробированы и неплохо согласуются с практическими результатами. Но остаются слабоизу-ченными процессы, происходящие в переходных режимах. Особенность эксплуатации данного класса электромеханических систем в том, что переходные или нестационарные режимы работы составляют 3040% эксплуатационного времени. Поэтому исследования в данной области обусловлены запросами практики и актуальны.
Постановка проблемы. Анализ современного промыслового оборудования показал, что применяемые приводы отдельного класса грузоподъемных устройств по физико-энергетической сущности можно условно разделить на несколько видов: привод от двигателя внутреннего сгорания, электропривод и гидропривод. Наибольшее распространение в рыбопромысловых механизмах получил электрический привод. На рис. 1 представлена структурная схема системы электрического привода [5].
Рис. 1. Структурная схема электрического привода
Основные преимущества электрического привода – высокий кпд, безопасность и простота управления, возможность реверсирования и регулирования в значительных пределах скоростей вращения вала двигателя и соответственно исполнительного механизма, постоянная готовность к действию. Также важным достоинством электрического привода является удобство осуществления дистанционного и автоматического управления. Во время работы промысловые лебедки испытывают нестационарные динамические нагрузки, которые зависят от большого количества факторов. Существующие методики расчета привода промыслового грузового оборудования имеют приемлемую точность и апробированы для стационарных режимов работы комплекса. Однако нестационарные процессы на данный момент изучены слабо, в связи с чем элементы комплекса с учетом запасов прочности
рассчитывают, принимая, что будут возникать нагрузки, превышающие расчетные в 1,5-2 раза.
Цель работы совершенствование методики расчета электромеханического привода отдельного класса грузоподъемных устройств на примере неводовыборочного комплекса, за счет чего будет достигнуто повышение эксплуатационной надежности и эффективности работы промысловой лебедки и системы привода на основе выбора рациональных параметров ее эксплуатации.
Результаты исследований. Неводовыборочный комплекс является частью грузового палубного оборудования промыслового судна кошелькового лова, который по популярности занимает второе место и уступает только траловому лову. Основой неводовыборочного комплекса является промысловая лебедка. В состав судовой промысловой лебедки входят: элементы привода (двигатель, соединительные муфты, редуктор); элементы управления (муфты включения, тормозные устройства, канатоукладчики и т.д.); исполнительные элементы (навивной барабан, фрикционный барабан); элементы обслуживания (система смазки, регулирования, охлаждения тормозов и т.п.); опорные элементы; элементы передач (передача к грузовому валу, грузовой вал, передача к канатоукладчику и др.). Обычно для привода промысловых лебедок применяются электродвигатели постоянного тока со смешанным возбуждением.
Промысловые лебедки относятся к отдельному классу электромеханических систем (ЭМС). Электро- механический привод (ЭМП) промысловой лебедки целесообразно представить в виде эквивалентной двухмассовой электромеханической системы, упрощенная схема которой изображена на рис. 2. Данное замещение реального объекта возможно без ущерба для практических расчетов, так как приведенные массы или моменты инерции крайних элементов составляют не менее 80% приведенного значения масс или моментов инерции всей системы.
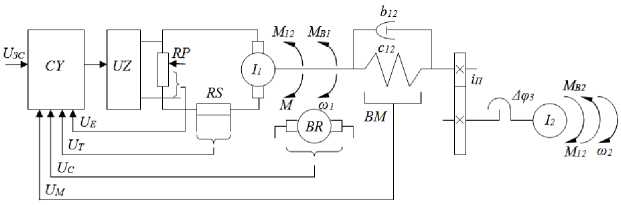
Рис. 2. Расчетная схема ЭМП:
I 1 и I 2 – суммарные моменты инерции масс установки, приведенные к валу двигателя и жестко связанные, соответственно, с валом двигателя и с выходным валом барабана; ω 1 и ω 2 – скорости вала двигателя и барабана; c 12 , b 12 – эквивалентная жесткость коэффициент внутреннего вязкого трения механических передач; M 12 – момент в упругом элементе; M – момент двигателя; M B1 и M B2 – прикладываемые к валу двигателя и барабана моменты сопротивления, в общем случае учитывающие влияние статической нагрузки, моментов трогания и внешнего вязкого трения
Для составления математической модели электрической части исследуемой системы привода (ЭЧС) допустим, что в исследуемой электромеханической системе электрические цепи удовлетворяют всем условиям квазистационарности, что допускает исследование методами теории электрических цепей. Необходимо также учесть, что в системе действуют потенциальные силы, диссипативные силы, неконсервативные обобщенные силы механической природы, пондеро-моторные силы. Диссипативная функция ЭМП состоит из электрической и механической диссипативных функций. При этом электрическая диссипативная функция не зависит от обобщенных скоростей q i и механическая диссипативная функция не зависит от токов i k .
При исследовании электромеханического привода отдельного класса грузоподъемных устройств, учитывающего переменность нагружения, в качестве обобщенной координаты принимаются угловые значения координат системы ф или линейные координаты x и заряды e k . Также необходимо учесть переменный момент, используя результаты, полученные при исследовании МЧС. Пондеромоторные силы в ЭМП определяются, в общем случае, принципом действия и конструктивным исполнением двигательного устройства. Для учета силового воздействия со стороны электропривода в математической модели привода необходимо учесть влияние ЭДС вращения Ед ( ^ ) , которая зависит от угловой скорости ^ t , а также влияние развиваемого двигателем момента Мд (ik , Фк ) , зависящего от значения тока i k в его электрической цепи и соответствующего потокосцепления Ф k .
С учетом этого система уравнений Лагранжа-Максвелла для исследуемого ЭМП будет иметь вид
iR + Ldt = Ек — ЕД ^ ^
d ( 5 L ) 5 L 8D „
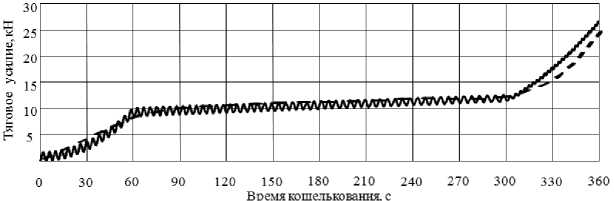
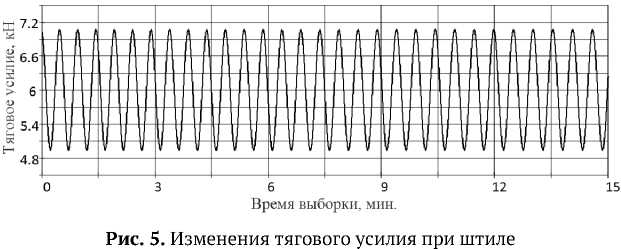
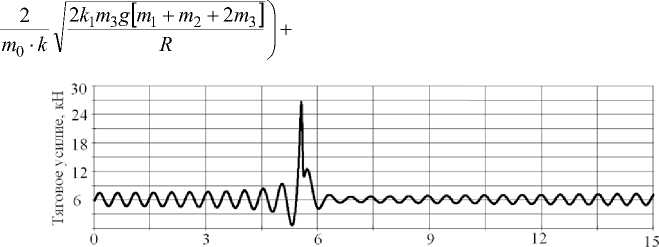
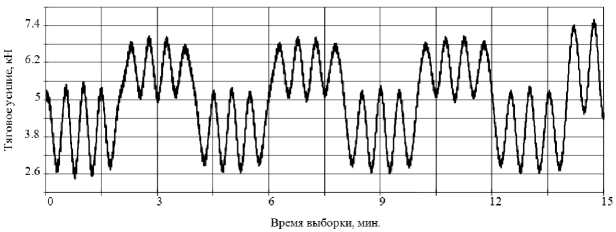
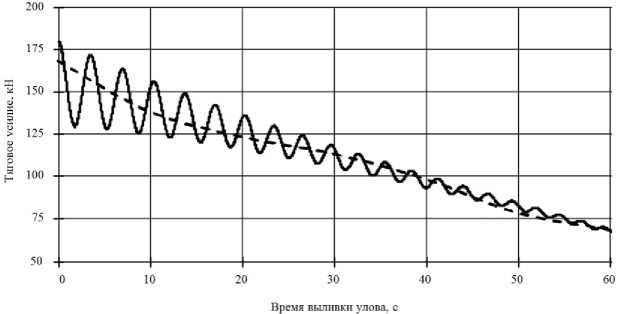
— I — 1 + — + —= FM, dt Vcqq J 8 q 8 При выборе рациональной схемы замещения механической части ЭМП следует по возможности выделить наибольшие и примерно одинаковые приведенные массы и моменты инерции, так, чтобы между ними находились элементы с минимальными коэффициентами жесткости. При получении обобщенной математической модели ЭМП с учетом упругих связей при описании механической части системы привода (МЧС) возникают наибольшие сложности, т.к. необходимо учесть различные виды нелинейностей, изменение параметров и характеристик системы как функции координат и времени. В работе были исследованы следующие процессы: подъем груза с переменной массой, изменение радиуса на навивочном барабане, следовательно, его момента инерции, свободные колебания концевых масс, возникающие при выгрузке, переменное сопротивление груза во время подъема, переменный момент вращения, влияние гидрометеорологических факторов. Все эти процессы можно достаточно точно проследить на примере неводовыборочного комплекса. При исследовании данного комплекса динамические модели МЧС были представлены в виде моделей с сосредоточенными параметрами, в которых число звеньев ограничено. Было принято, что инерционные свойства системы учитываются массами, которые сосредоточены в приведенной массе навивочного ва-ерного барабана и приведенной массе системы «ваер – орудие лова – объект добычи». Эти звенья соединены безынерционными упругодиссипативными геометрическими или кинематическими связями. Использование такого перехода от реальной системы к эквивалентной на практике приводит к тому, что в механизме и его приводе выделяются наиболее массивные элементы и податливые участки кинематической цепи, а инерционные, упругие и диссипативные свойства остальных элементов учитываются с помощью приведенных эквивалентных значений соответствующих параметров. Промысловая лебедка задействована на следующих этапах рыбопромысла: кошелькование (выборка стяжного троса), выборка невода и выливка уловка [1-3]. Наиболее энергозатратным является процесс кошелькования. По времени он составляет до 70% от всего технологического процесса. Согласно экспериментальным данным подъем груза грузоподъемными устройствами можно изобразить в виде трапецеидальной тахограммы. Поэтому и процесс кошелькования целесообразно разделить условно на три этапа, во время которого изменяется не только длина выбираемого стяжного троса, но и форма (рис. 3) и масса стягиваемого в воде невода, что оказывает значительное влияние на гидродинамическое сопротивление в исследуемой системе, а, следовательно, и на силу натяжения на ваерном барабане [6]. 4 Го X Рис. 3. Изменение формы невода в процессе кошелькования Математическая модель динамики движения системы «промысловое судно - стяжной трос - невод» с учетом переменных параметров груза была получена в виде уравнения Лагранжа второго рода тогда будет иметь вид [7]. - для первого и второго этапов кошелькования q 2g dl dф dt dt d2l _ ( dl)2 +l(1 + ф)—-2ф\ — \+ dt2I 2l2d2ф 3 dt2 , a l (t) q- - EFфRdx - для третьего этапа [ 2-2(ql + 3Q) d^ + - (ql + 2 Q )(1 + Ф) dl + 2 g L 3 dt2dt + 4l (ql + 3Q) -d^ - ql (1 + фf \ + 3 dt dtV 2 dl „dQ dф dlddOA + -l2\ q + 3 \ +1\ q + 2 \x 3 V dt dt) dt V dt dt) dl / ql) д l f) x (1 + ф) = 11 Q + — I - БРф- - x ' dt V 2) дф где q - вес погонного метра троса; О - вес колец невода, подходящих к канифас-блокам выстрела на третьем этапе кошелькования; R - сила гидродинамического сопротивления, зависящая от переменной площади сечения невода, перпендикулярного потоку ^ = -J[x2(У)-х1(У)]dy. Hi По полученным теоретическим зависимостям было проведено компьютерное моделирование, результаты которого имеют отклонение от экспериментальной динамограммы в пределах 7% (рис. 4). Рис. 4. Теоретическая и экспериментальная динамограммы натяжения троса во время кошелькования Следующим этапом технологического процесса добычи рыбы является выборка невода вместе с уловом. При выборке кошелькового невода усилие, действующее на неводовыборочную машину, складывается из двух величин - сопротивления невода при его подтягивании к судну и силы тяжести участка невода (часть в воде, часть в воздухе), которая непосредственно воспринимается лебедкой. По мере выборки часть невода, которая находится в воде, уменьшается, и сопротивление ее уменьшается. Следовательно, тяговое усилие в процессе выборки кошелькового невода постепенно уменьшается и под конец выборки становится минимальным и равным силе тяжести участка невода, которая непосредственно воспринимается лебедкой. Процесс выборки невода значительно усложняет качка судна. В результате волнения и качки судна к нагрузкам, которые определяются гидродинамическим сопротивлением невода и его весом, добавляется еще периодическая динамическая составляющая. При построении математической модели выборки невода уменьшается воздействие выталкивающей силы, и, как следствие, увеличивается вес невода. В силу того, что выборка осуществляется с постоянной скоростью, принято, что вес невода изменяется по линейному закону kim3дф, где к 1 - коэффициент пропорциональности, зависящий от температуры воды, ее солености, скорости выборки невода. Радиус и масса барабана в процессе выборки невода изменяются, также как и при кошельковании. Однако, оценить их достаточно сложно, так как на барабан наматывается теперь не трос с постоянным сечением, а жгут невода. В силу принятых допущений математическая модель процесса выборки невода имеет вид [mi + m 2 + 2 m 3 ] • d 2ф 1 ,. + - m 0 кФ dt2 2 + 2k1m3gR ф = 2 M (t) 2 Fc R2 R - вращающий момент на валу барабан имеет постоянное значение, и выборка осуществляется при штиле T = Fc + kim3 g I M0Fc- + [ Rki m 3 g ki m 3 g где m1, m2, m3 – приведенная масса соответственно барабана, жгутоформирователя, невода с уловом; M(t) – вращающий момент на валу барабана. При исследовании данного ЭМП были рассмотрены различные случаи воздействия внешних факто- f2 12 ki m3 g[mi + m 2 + 2 m 3 ] + к sin -----л --------------------- I m0• k V R + K21 cos V m 0 • k 2ki m3 g[mi + m 2 + 2m 3]) R J ров и получены аналитические зависимости для опре- деления силы натяжения: - процесс выборки происходит в условиях бортовой качки +К 22 cos vm 0 • k 2 ki m 3 g [mi + m 2 + 2 m3 ] R + K3 (t )sin pt + K4 (t )cos pt} ; T = Fc + kim3g1 -M0---Fc- + 3 [ Rk i m 3 g ki m3 g + Кi2sin V Время выборки, мин. Рис. 6. Изменение тягового усилия с учетом качки.Эффект резонанса - осуществляется прерывистый режим работы лебедки Ti = Fc+kim 3 g M0+ Mi 2Rk1m3g Fc k1m3g + + Ki3 2 ki m 3 g [mi + m 2 + 2 m 3 ] R f 2 /2ki m 3 g[mi + m 2 + 2m 3]) + к23 cos -------------------------- + I m 0 • k V R J + К3 (t )sin pt + К4 (t )cos pt + m • f nn ) r f nn л sin —t + L-, „ cos —t > V 1 J 2n V 1 J/J + Д Li n n =i \ Рис. 7. Изменение тягового усилия при прерывистом режиме работы Следующим этапом технологического процесса является выливка улова. После остановки органа навивки (барабана) механическая часть ЭМП промысловой лебедки «распадается» на две независимые одномассовые системы. Первая – сбегающая ветка жгута невода, вторая – набегающая ветка жгута невода с уловом. В этих двух механических системах после остановки осуществляются независимые свободные колебания концевых масс. Характеристики колебательных процессов в системе определяются массами, жесткостью элементов и коэффициентами диссипации, а также начальными условиями в момент остановки барабана. В это время возникают максимальные динамические нагрузки, знание которых важно при проектировании. Математическая модель свободных колебаний улова во время выливки. Отсюда аналитическая зависимость для определения тягового усилия может быть записана в форме T = m о (1 - kt) + mA 3н g + cxx(t) где 2b x (t ) = em 0 k^ x^ K 1cosl--^= I v m0kTc + K2 sin — V m 0 kVc; имеет вид + < — п cx X 1 | 1 + m + 3 н I 1 + 1mH m0 (1 — kt) + 1mH m 0 (1 —kt)+1 тн d2x _ dt2 + dx + а^—+ cxx = 0 dt где 8 - логарифмический декремент колебаний; а -поправочный коэффициент; m = m0(1 - kt) - масса Экспериментальная динамограмма и динамограмма, построенная по теоретической зависимости, изображены на рис. 8. Как видим, они хорошо согласуются, имея расходимость в пределах 8%. Полученные аналитические зависимости позволяют также качест- венно оценить процесс, находить характеристики движения, такие как период, амплитуду, моменты попадания в резонансную зону. Рис. 8. Теоретическая и экспериментальная динамограммы натяжения троса во время выливки улова Выводы: 1. Получена комплексная математическая модель электромеханического привода отдельного класса грузоподъемных устройств на примере неводовыборочного комплекса, характерной особенностью которого является переменность нагружения. 2. Получены аналитические зависимости для определения силы натяжения стяжного троса, которые могут быть использованы на этапе проектирования. 3. Применение результатов исследования, изложенные в данной статье, на этапе проектирования могут обеспечить повышение эксплуатационной надежности и эффективности работы системы привода на основе выбора рациональных параметров эксплуатации.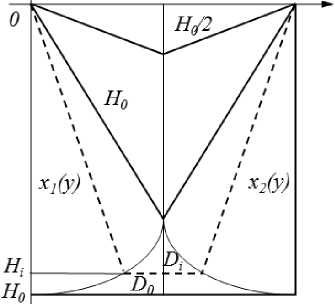
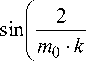
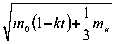
Список литературы Совершенствование методов расчета электромеханического привода с учетом переменности нагружения
- Торбан, С.С. Промысловые механизмы для комплексной механизации кошелькового лова рыбы. -М.: Пищевая промышленность, 1971. 384 с.
- Дверник, А.В. Устройство орудий рыболовства/А.В.Дверник, Л.Н. Шеховцев. -М.: Колос, 2007. 272 с.
- Карпенко, В.П. Механизация и автоматизация процессов промышленного рыболовства/В.П. Карпенко, С.С. Торбан. -М.: Агропромиздат, 1990. 464 с.
- Ивановская, А.В. Анализ факторов, влияющих на эффективность работы неводовыборочного комплекса/А.В. Ивановская, Е.В. Богатырева//Современные проблемы теории машин: сб. науч. трудов междунар. науч.-практ. конф. -г. Новокузнецк, 19-20 мая 2015 г. С. 137-141.
- Рыбак, А.Т. Совершенствование методики расчета системы приводов технологического оборудования/А.Т. Рыбак, И.В. Богуславский//Вестник машиностроения. 2010. №10. С. 39-46.
- Ивановская, А.В. Формализация динамики работы неводовыборочного комплекса на этапе кошелькования/А.В. Ивановская, Е.В. Богатырева//Вестник Харьковского национального технического университета сельского хозяйства: . 2015. Вып. 163. С. 178-185.
- Ивановская, А.В. Исследование динамических процессов при работе неводовыборочного комплекса/А.В. Ивановская, Е.В. Богатырева//Инновационные технологии в науке и образовании ИТНО-2015: сб. науч. трудов междунар. науч.-практ. конф., посвященной 85-летию ДГТУ. г. Ростов-на-Дону -п. Дивноморское, 7-10 сентября 2015. С. 198-203.


