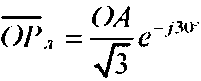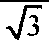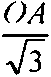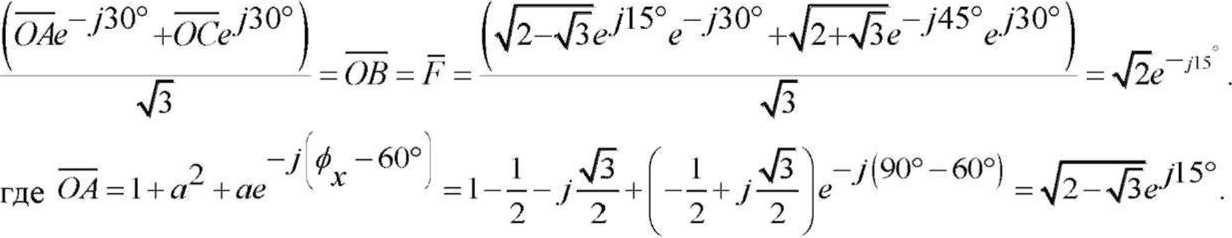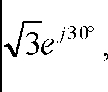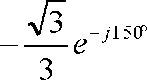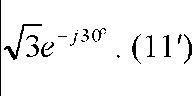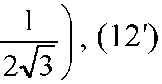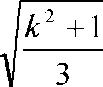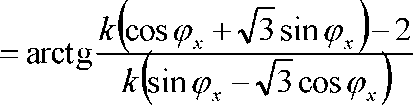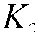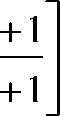Совершенствование методов расчета симметричных составляющих токов и напряжений

ГОСТ 13109-97 [1] регламентирует показатели качества электроэнергии. Одним из показателей является коэффициент несимметрии по напряжению обратной последовательности К2и.

Анализ литературных источников, например [2, 3] и ряда других, показал достоинства и недостатки предпринятых попыток решить задачу определения К21 j при помощи «метода трех вольтметров».

Среди основных недостатков можно отметить следующее: громоздкость аналитических выражений для определения модулей симметричных составляющих [2], что предполагает составление вспомогательных расчетных таблиц, которые весьма громоздки для использования в повседневной инженерной практике:

• -    неполнота получаемой информации, (отсутствие формул для аргументов

СС) и, как следствие, невозможность определить комплексный коэффициент несим-метрии, например для целей симметрирования режимов электрических сетей;

• -    ограниченная область применения. Например, в [1], в случае крайней несим-метрии при Uab=0 и Ubc=Uca, дроби в подкоренном выражении дают неопреде-

• Ulc+UL 0 ленность вида------- — ;

• -    упрощение формул зачастую приводит к значительным погрешностям [3] получаемого результата;

• -    графики, номограммы при всей своей наглядности обладают низкой точностью и весьма неудобны при обработке больших массивов данных, в том числе и на компьютерах.

Задачи, решаемые в данной статье, вытекают из вышеизложенного и заключаются в следующем:

• —    разработать математическую модель, позволяющую исследовать закономерности изменения симметричных составляющих на окружности в 360 . Данная модель должна давать адекватные результаты во всех режимах работы электрических сетей: от КЗ (двухфазного без земли) до обрыва фазы, включая полнофазные несимметричные режимы, а также и симметричный. Возможность использовать предлагаемую модель для решения задач о СС в стандартной постановке (т.е. при задании модулей и аргументов несимметричных линейных токов или напряжений);

• -    повышение точности вычислений всех составляющих несимметрии при значительном снижении сложности используемых формул, алгоритмов, затрат интеллектуального труда и простейших вычислений для K21- в соответствии с [1];

• —    получение результата в любом интересующем виде (алгебраическом, показательном, тригонометрическом) в зависимости от целей исследования, при непременном условии простоты используемых формул, как основы инженерной методики расчета СС.

А втором предложена следую щая формула для уравнения окружности в векторном виде:

F - ҒҮ + а^ +ае 'ІФх где F^1 =Fe /12GF = а1 - для окружности единичного радиуса, и

ҒАа = Ғе^

где а и сГ - операторы поворота соответственно на 120^J и (-120^J).

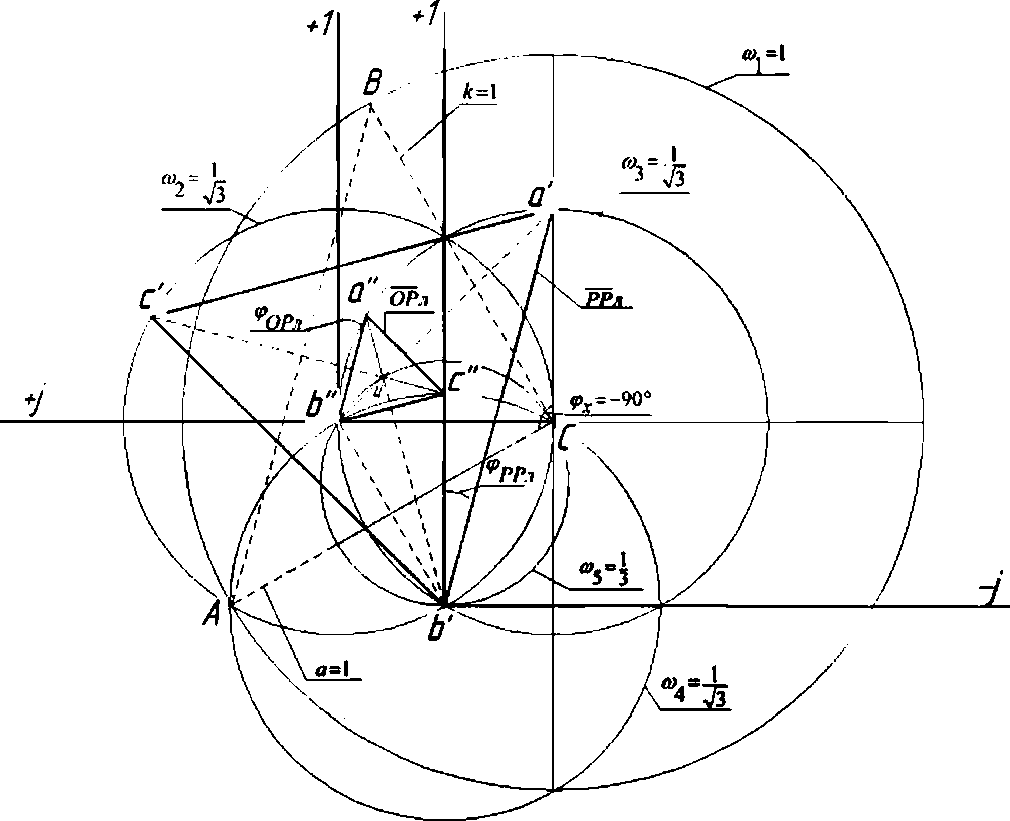
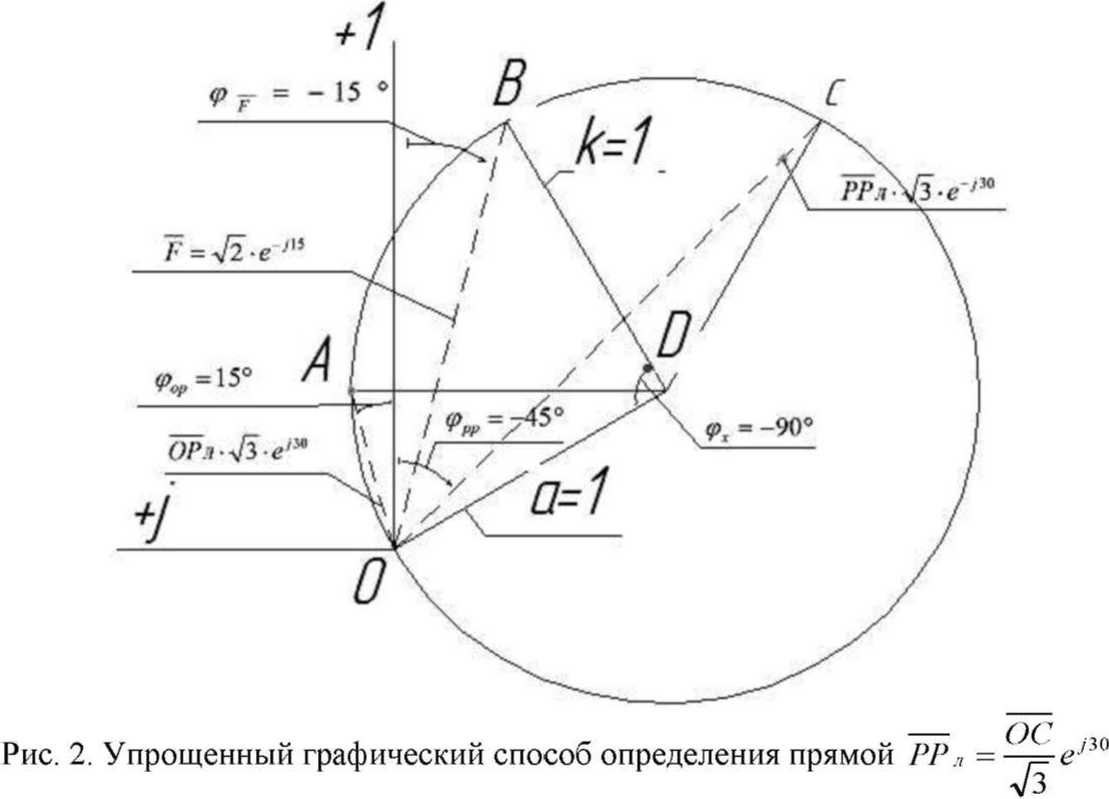
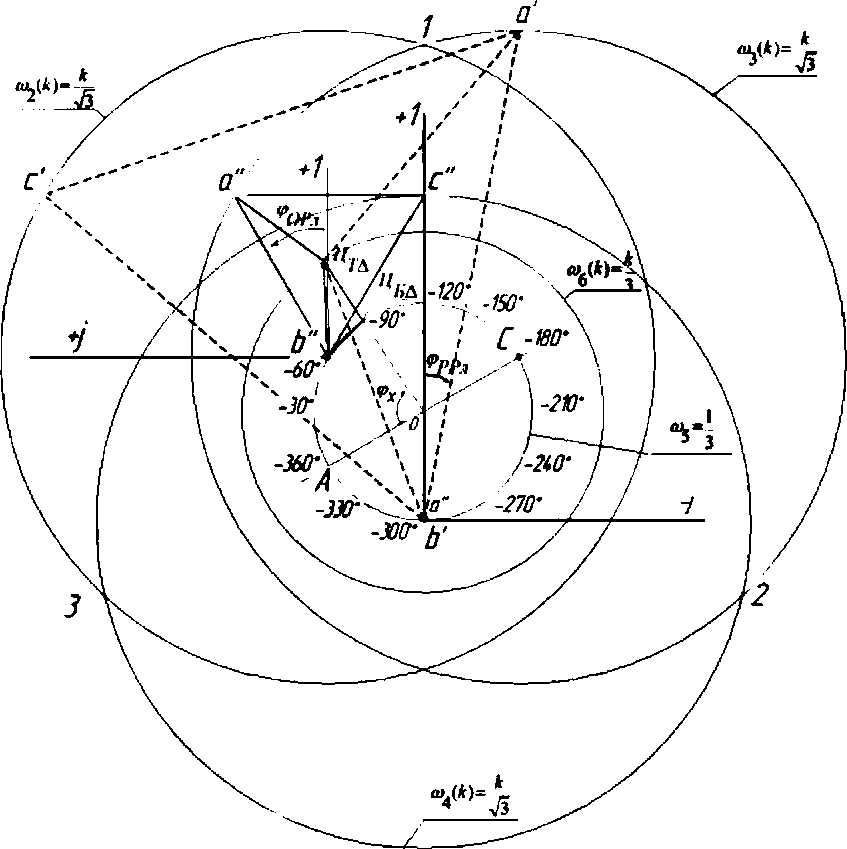
Известно, что 1 іліл“=0. но если оператор поворота а вращать по часовой (или против) стрелке путем умножения его на оператор поворота е J

На рисунке 2 показан Ба при (з =-90° и 1<-1 Тогда, в соответствии с (1), векторное уравнение F примет вид

Теперь, если последовательно, например при помощи метода Фортескью, определить линейные СС (симметричные составляющие), РР л и ОР л - векторы линейных параметров1 прямой и обратной последовательностей для стягивающей стороны AB = F (см. рис. 1), то выявятся следующие закономерности.

При повороте вектора а (например) по часовой стрелке по окружности ^=1, векторы (№ -) и (ОР л) последовательностей будут перемещаться по окружностям „ 1                                      1

радиуса К = —j=, одна из которых со₃ = —= л/3                         V3

описана из того же центра, что и окружность радиуса гц =1, а вторая, ац, из точки 1

на оси +j, тоже радиусом со₂ -—р и пересекает со^ в центре (в точке С), третья,

6У₄ = —р, из точки пересечения первых двух, Ь', как указано на рисунке 1. Центры окружностей (о₂, <о_л и со₄ обозначены, соответственно, как Ь", с, Ь'.

Рис. 1. Определение РР_Л и ОР_Л последовательностей для Бд, (при <9_ү= 90°. k = 1)

с применением комплексной циркульной плоскости (термин автора), где Бд - базовый несимметричный треугольник (АВС), построенный на окружности единичного радиуса ^ = 1, две стороны которого (неподвижная (АС) и подвижная (ВС)) - радиусы этой окружности; третья сторона Бд - стягивающая сторона двух вышеназванных,

к -

= 1 о.е. - средняя (подвижная) сторона несимметричного Б \

Центры тяжести всех треугольников (исходного несимметричного(АВС), РР л и ОР л) перемещаются в функции <р по окружности радиуса <у5 = -, центр которой

1 находится на векторе а на расстоянии — а от центра окружности f^ = 1. Найден упрощенный способ определения прямой

= РР _ч и обратной         = OP_:i

V3                    V3

последовательностей, относительно стягивающей (F ) стороны Бд (см. рис. 2).

Алгоритм нахождения РР _л и ОР_Д в упрощенном виде можно свести к следующему:

Если вектор 7*’ несимметричного Бд ОВД равен:

F = \ + а2 + aF"p’',

— ОА и обратной ОРч = —=е /3°, последовательностей Б\ОВД

V3

то линейный вектор прямой последова тельности РРл\

7з             7з а линейный вектор обратной последова тельности ОР л

2 , М_х -60^ а + ае ^VVx

е У»

-(4)

где е^ (для РР ;О ^{и е} '^ (д^ляОР л) -

ОС операторы поворота векторов —^ и

V3

до совмещения их с вектором К =ОВ. Для стягивающей стороны F Б_х векторы РРл =а'Ь' и ОР л -а"Ь" сонаправлены (см. рис. 1).

Таким образом,

(£^ІІ^У^       (5)

V3

т е. стягивающая (^) сторона исходного несимметричного Б_х равна геометрической сумме двух векторов ОА и ОС, один из которых ^ОС\ получен поворотом исходного вектора К=1 на дополнительный угол (-60°) и ОА - на угол (+60 ), разделенных на Vb и повернутьгх соответственно на е ^,4V (для определения ОР их} и е*^ (для определения РРбх\

Покажем работу (5) на Бд, изображенном на рисунках 1 и 2.

И

ОС = I + J +ae-^M+w = 1 + а² +ае^^5а' = V2 + ТЗе"-'⁴⁵".

Из рисунка 1 видно, что если воспользоваться стандартной процедурой перехода от линейного вектора ОР_л tOh" к фазному ОРф = цЬ'¹ =----/=---= ОР ф, (6)

то для F Бд получим обратно направленный фазный вектор обратной последовательности. Обратно направленный фазный вектор прямой последовательности полу-

—*   ~РР чим как РР ф =---=— .             (7)

V3

В рамках предлагаемого метода, несимметричный ТОП (треугольник общего положения, у которого, в общем случае, все стороны различны по модулю, далее Тд, рассматривается как сумма Бд, плюс

Исследования показали, что Цтд перемещается относительно Цбд в направлении, параллельном вектору к на величи- к~ 1 /(12(У ну, пропорциональную —-—е

Уравнение ОР фі-х, в соответствии с (4), (6) и рисунком 3 примет вид

= ОТф+ — е№^ =

- / 60                                            /     1

=------ 1 + йг -vae ■ н--e^j .

3 V                     /    3

Алгоритм нахождения фазных и линейных С С Тд представлен на рисунке 3.

Рис. 3. Определение фазных и линейных симметричных составляющих Тд-треугольников

Из рисунка 3 следует, что векторная разность

ОР фт^ -         = РР фта ,       (9)

Л _ s где —неподвижный вектор соеди няющий точки Ь" и Ь'.

Определившись с обратными фазными векторами СС ТЛ, переходим к истинным линейным векторам СС по формулам:

ОР_лТ, =ОРфп^^31Г,        (10)

РР,п =рр'фт^е ■'^от,        (И)

В развернутом виде формулы (10) и (11) примут вид:

ОРЛ^ =

— 1 + а2 +        1 + — е2І12(ғ-й 1

3   \                    /    3

^{5 V} 0 ,  2 ,        6(0^  1 ;(12СР

3 v                      7     3

(10')

Из формул (10') и (1 Г) получаем сокращенные выражения в показательном виде, в о.е.: ___      „-/30" г

РР^ =Ц=- ке Аф- 1261 +1 ,(12)

V3 L

____        , /90" г, п

ОР гл =—ке х +1 ,(Ь)

Л L J

После применения тригонометрических формул для суммы и разности углов, получаем алгебраический вид сокращенных выражений (12) и (13) в о.е.:

—    (к sin          (к cos со

РРтл = --+ - + / --Л

( Vs 2J V3

—т,     (Asm 67    к ]    [ к            к  .         1

ОРтЛ - ---Л"--COS (О + / --,= SIH --Sin 0 —/=

I 2V3  2  m            2 V3

(13’)

Для модуля l/VyJ вывод формулы приведем полностью, а для <7/’7Л запишем без

вывода:

к² sin²ф. 2£sin0. 1   1 к¹ cos²ф,. 2ксо$ф. 1     1

----— +--- + — +----— +--—— + —

3 Л 2 4    3 Л 2Л И

к +1 к ( г- .

--' “ (у 3 sin ф_х - cos Ф_х 3      3 ^х

о.е.

Кл| =

sin^x + cos с? I, о.е.

Все вышеприведенные формулы для несимметричных треугольников линейных параметров результат дают в относительных единицах (о.е.), т.е. по сути являются переводными коэффициентами для определения СС в именованных единицах. Если принять за параметр напряжение U, то

U ■                f с можно записать: а = —— = 1; к - ——;

^min

= гДе U^Yq,, U^ - соответ- ственно минимальная, средняя и максимальная величины измеренных напряжений (модулей). Тогда

Ф_х = arccos--угол между {/_mjll и

2к

U_cp (или а и к)^ определенный по теореме косинусов для Т.\, выраженного в о.е.

л/Ззіп фх +cos^. = -2 cos (^ +120°), формулы можно записать несколько иначе:

иі№^ -      + у cosfe + 120 )

Формулы для определения модулей СС в именованных единицах:

|77,>|rU-r71(,,^      (17)

КГ1+4+«+В).    (18)

Из формул (12') и (13') получим выражения для аргументов СС:

4% - arctg

2к cos tp_s -1 2к sin ф_х + л/з

4%

Для проверки правильности вычислений нужно использовать следующие фор-

мулы:77_ = F=O_lA=V*-, (21)

или ^ | = \F\ = ^KW + WTH^d (В),       (22)

, = |ЦУ>иЦ_4+_|у!+_ KJcos^KJccM, ’

Коэффициент несимметрии по напряжению обратной последовательности, в соответствии с ГОСТ 13109-97

IL         kA™ I • к² +1 + 2к cosb +120^о)1°'

-100% = L+^U------- ---------

U_H                  J3Uh

к„. = ^.ioo%= - и,

к² +1 + 2к cos(^._Y +120°) к² +1 + 2к cos(^_x -120°)

100%.

При решении вопросов, связанных с симметрированием, используется комплексный коэффициент несимметрии по току обратной последовательности:

А, = — е^м--^ф'-* • 100% = е"'^№

£ ^"/(^,+12+)

100%

Выводы

Предложенная методика позволяет определять С С в полном виде (модули и аргументы) на окружности 360° доступными в повседневной инженерной практике вычислительными средствами, без применения вспомогательных таблиц, номограмм и сложных алгоритмов.