Совершенствование многономенклатурных систем управления запасами в торговле аннотация
Автор: Старикова Л.Н., Силин А.В.
Журнал: Экономика и социум @ekonomika-socium
Статья в выпуске: 6-3 (19), 2015 года.
Бесплатный доступ
В данной статье рассмотрены проблемы оценки готовности многономенклатурных систем управления запасами торгового предприятия. Проанализированы характерные особенности путем разработки и внедрения логистических инноваций в управление запасами, в том числе многономенклатурными системы управления запасами.
Логистика, многономенклатурные системы управления товарными запасами, марковские модели
Короткий адрес: https://sciup.org/140115209
IDR: 140115209
Текст научной статьи Совершенствование многономенклатурных систем управления запасами в торговле аннотация
В данной статье рассмотрены проблемы оценки готовности многономенклатурных систем управления запасами торгового предприятия. Проанализированы характерные особенности путем разработки и внедрения логистических инноваций в управление запасами, в том числе многономенклатурными системы управления запасами.
Ключевые слова: логистика, многономенклатурные системы управления товарными запасами, марковские модели.
Одним из главных направлений интенсификации деятельности торговых предприятий является повышение степени готовности их систем управления запасами (СУЗ) к обслуживанию клиентов и снижению уровня потерь от возможного дефицита товаров.
Решить эти задачи можно путем разработки и внедрения логистических инноваций в управление запасами, в том числе многономенклатурными СУЗ. Главными причинами снижения готовности СУЗ к обслуживанию и увеличения потерь от дефицита остается не всегда обоснованный выбор методов управления и контроля запасами.
Для того, чтобы управлять товарными запасами необходимо планировать определенный объем и структуру запасов в соответствии с поставленными перед торговой организацией целями и контролировать, чтобы товарные запасы постоянно отвечали установленным критериям. Управление должно быть систематическим. Иными словами, должен быть предусмотрен некий организационный механизм, который сам по себе обеспечивал бы поддержание нужных товарных запасов.
Запасы на предприятии образуются по двум основным причинам.
-
1. Несоответствие объемов поставки объемам разового потребления.
-
2. Разрыв во времени между моментом поступления материала и его потреблением.
Товарные запасы могут образовываться на всех стадиях товародвижения: на складах производственных предприятий, в пути, на складах оптовых и розничных товарных предприятий.
Целью управления запасами является нахождение такой их величины, которая, с одной стороны, минимизирует общие затраты по их поддержанию и, с другой стороны, была бы достаточной для успешной работы предприятия. Первым этапом процесса управления является идентификация всех затрат по завозу и хранению запасов.
Задача управления запасами, в общем случае, формулируется следующим образом: определить оптимальный размер запаса, размер, частоту и сроки поставки заказа, минимизирующие суммарные затраты. В затраты обычно входит стоимость закупки, доставки и хранения продукции.
Необходимость контроля состояния запасов обусловлена повышением издержек в случае выхода фактического размера запаса за рамки, предусмотренные нормами запаса. Контроль состояния запаса проводится на основе данных учёта запасов и может осуществляться непрерывно, либо через определённые периоды [1; 2].
Исследуемое торговое предприятие - ООО «СуперСтрой-Пермь», входящее в состав ООО «Трест СКМ». Сокращенное наименование организации «ООО «Трест СКМ» - крупнейший в Урало-Сибирском регионе и первый по количеству магазинов в России оператор на рынке строительных и отделочных материалов, работающий с 1993 года. Постоянный ассортимент – более 3,5тыс. наименований товара.
Предметом основной деятельности предприятия является оптовая и розничная торговля стройматериалами.
Уровень товарных запасов в торговом предприятии ООО «СуперСтрой-Пермь» контролируется с помощью программы «Account». В программе установлен расчет уровня товарных запасов по системе «минимум-максимум», который ориентирован на ситуацию, когда затраты на учет запасов и издержки на оформление заказа настолько значительны, что становятся соизмеримы с потерями от дефицита запасов. Поэтому в этой системе заказы производятся не через каждый заданный интервал времени, а только при условии, что запасы на складе магазина в этот момент оказались равными или меньше установленного минимального уровня. В случае выдачи заказа, его размер рассчитывается так, чтобы поставка пополнила запасы до максимально желаемого уровня.
Для примера, был проведен анализ работы МСУЗ торгового предприятия ООО «СуперСтрой-Пермь» на предмет определения объема среднего уровня запасов, параметра продаж по периодам и уровня упущенных продаж по одной из групп товаров.
Для определения сходимости результатов по вероятности дефицита, «упущенной выгоды» по товарным позициям, при реализации модели многономенклатурной МСУЗ «минимум – максимум», произвели расчет фактических параметров за один квартал текущего года.
Для этого провели расчет анализа уровня запасов по исследуемой группе товаров в ООО «СуперСтрой-Пермь» за 3 квартал 2014 г., как показано в табл. 1.
Таблица 1 - Упущенные продажи по группам товаров ООО
«СуперСтрой-Пермь» за 3 квартал 2014 г.
|
Показатель |
Квартал |
Всего (тыс. руб.) |
Среднее значение |
||
|
Май |
Июнь |
Июль |
|||
|
Количество реализованных товаров (ед.) |
400 |
500 |
500 |
1400 |
467 |
|
Выручка (тыс. руб.) |
264,92 |
333,29 |
331,19 |
927,34 |
309,1 |
|
Сумма упущенных продаж (тыс. руб.) |
95,37 |
119,98 |
115,91 |
331,26 |
110,42 |
Оценим долю упущенных продаж в общем объеме выручки:
Dvп = -УП x 100% = , 6 x 100% = 35,7 = 36%
УП TR 927,34
где, DУП – доля упущенных продаж, %;
CУП – сумма упущенных продаж, тыс.руб.;
TR – выручка, тыс. руб.
Таким образом, по результаты расчета упущенных продаж по группам товаров за три месяца текущего года потери составили - 331,26 тыс. руб. или 36% от выручки, причем основной причиной этого являлось отсутствие каких-либо товаров на складе.
Для оценки готовности к обслуживанию и эффективности МСУЗ по вероятности возникновения дефицита, его величине и среднему времени его существования широко применяются марковские модели и методы систем массового обслуживания (СМО) [3].
Ниже приводится один из подходов расчета этих параметров для МСУЗ, используемых стратегию двух уровней «максимум-минимум» (Jmax, Jmin), на примере группы из 4-х товаров, реализуемых в течение полугода (при Т = 180 дней). Исходные данные оптимальных параметров поставок товаров представлены в табл. 2.
Таблица 2 - Параметры оптимальных поставок товара
|
Наименование и класс товаров |
Потребность в товаре за период Qi(ед) |
Оптим. объемы заказов qi(ед) |
Объем в грузовых единицах gi (у.г.е.) |
Средний уровень запасов Ji cp (руб.) |
Число заказов товаров ni, N∑ |
Периоды поставки заказов tiП (дн.) |
|
М1 (А) |
1000 |
50 |
2 |
1000 |
10 |
18 |
|
М2 (В) |
1000 |
100 |
4 |
500 |
5 |
36 |
|
М3 (С) |
800 |
100 |
4 |
400 |
4 |
45 |
|
М4 (D) |
400 |
100 |
4 |
300 |
4 |
45 |
|
Σ |
14 |
2200 |
23 |
Рассмотрим параметры марковской модели для определения вероятности дефицита при реализации модели МСУЗ типа «минимум -максимум» для 4-х видов товаров, изображенной на рис. 1
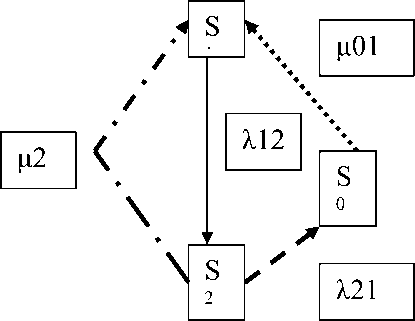
Рис. 1. Марковская модель MСУЗ для двухуровневой системы управления запасами «минимум - максимум»
На рис. 1 приняты следующие обозначения для данных модели:
-
– S1 – исходное состояние МСУЗ, при котором уровни текущих запасов JТЗi n товаров всей номенклатуры пополнены до максимальных значений Jmax или находятся в пределах между максимальным и минимальным их значением Jmin i, т.е. выполняется условие Jmax i ≤ JТЗ i < Jmin i;
-
– S2 – состояние МСУЗ, при котором уровень текущего запаса любого из товаров достигает минимального уровня текущего запаса Jmin I и возникает угроза дефицита по этому товару;
-
– S0 – состояние МСУЗ, при котором уровень текущего запаса любого из номенклатуры товаров находится в дефиците до момента их очередной доставки;
-
– λ i,j – интенсивность перехода МСУЗ из состояния i в состояние j , соответствующее расходу запаса того или иного товара номенклатуры;
-
– µji – интенсивность перехода МСУЗ из состояния j в состояние i ,
соответствующее пополнению запаса того или иного товара из номенклатуры.
Уточним сущность значений интенсивностей переходов.
M
m ij П ij m=1
состояние j ,
,
λm де, ij - интенсивность перехода из состояния i в соответствующее среднему дневному расходу запаса m –го товара из номенклатуры;
-
t П – пери од поставки (или контроля);
-
m , - количество видов товаров в номенклатуре.
M
^ i=tn xZ ^m m=1 , . (3) .
где, µ ji – интенсивность перехода из состояния j в состояние i, соответствующее пополнению запаса m – го товара из номенклатуры;
m , – количество видов товаров в номенклатуре.
Для данной модели приведем систему, состоящую из уравнений Колмогорова [3]:
P 1 X ^ 12 = P 2 X ^ 2 1 + P0 X ^ 0 1
P
o
+P
1
+P
2
=
1
Из системы уравнений (4), путем подстановок, находим выражения для расчета вероятности нахождения МСУЗ в том или ином состоянии S:
p _
A
)1
X (
^
20
+
^
21
)
x p
^
20
X
^
12
< P =
^
01
xP
2
^
20 0
P
0
=
I I
^
01
!
№01
x
(
^
20
+
^
21
)
^
20
^
20
^
12
-
1
Интенсивности прямого
X
ij
и обратного ц
ji
перехода из одного состояния S
i
в другое S
j
и обратно будет пропорциональны отношению среднего расхода единиц товара q за период поставки tП, что аналогично среднему дневному потреблению товара за период Т или tП, то есть:
^
i
=
Q
i
qi
T
i
t
Пi
Аналогичным образом находятся интенсивности пополнения запасов µi,j, учитывая среднее время доставки заказа от поставщика.
Рассмотрим интенсивности потребления
^
i,j с учетом особенностей модели СУЗ типа «минимум-максимум», представленной на рис.1.
В общем случае, интенсивность потребления будет носить случайный характер и будет распределяться по закону Пуассона.
Интенсивность потребления
1
1,2 характеризует переход системы из S1 в состояние S2. Это предусматривает периодический расход всех товаров А, В, С, D одновременно, интенсивность расхода каждого из которых по формуле (6) будет равна:
Л = = 50 = 2,8 ед / дн Л = 100 = 2,8 ед / дн tП 1 18 2 36 , ; ;
Л
=---=
2,2
ед
/
дн
3
45
;
Л
= =
2,2
ед
/
дн
4
45
Суммарная дневная интенсивность перехода
1
1,2 по всем товарам будет равна:
ls
=
2,8
+
2,8
+
2,2
+
2,2
=
10
ед/дн.
Пополнение запасов с центрального склада происходит, когда почти все запасы исчерпаны, для нашего случая, это 1 раз в 45 дней, тогда интенсивность перехода 11,2 из S1 в S2 пропорциональна суммарной интенсивности расходования всех товаров 12 в течение 45 дней. Исходя из этого, формулу (7) можно записать в следующем виде:
1Ъ
2 =
Л
х
tn
=
(2,8
+
2,8
+
2,2
+
2,2)
х
45
=
450
ед/дн. (
Также пополнение товаров может происходить и с регионального склада между циклами пополнения товаров с центрального склада, когда некоторые из товаров переходят в состояние S0 дефицита. Интенсивности пополнения запасов µ01 находятся с учетом того, что формирование заказа происходит, когда объем дефицита становится равным примерной грузовместимости транспортного средства для его доставки от поставщика и происходит в течение 5 дней. В самом деле, не гонять же автомобиль за одним ящиком гвоздей. Будем полагать, что, в общем случае, формирование заказа начинается при наступлении дефицита по всем товарам номенклатуры, тогда максимальная интенсивность перехода будет равна: 50 100 100 100
---= 70
ед
/
дн.
^
oi =--1---1---1--
01
5 5 5 5
Для нашего примера, такой же заказ будет сделан на центральный склад и на 36 день, когда будут пополнены все товары. Тогда интенсивность перехода µ21 из состояния S2 в состояние S1, будет пропорциональна интенсивности µ01 пополнения всех запасов, через 36 дней, и равна:
^
i =
^
i =
70
ед
/
дн
.
В общем случае, вероятность перехода системы из состояния S2 в состояние дефицита S0 может произойти обвально, ближе к окончанию цикла потребления товаров, и быть пропорционально более сложному потоку событий, например, потоку Эрланга n–го порядка, что значительно осложнит расчеты. Поэтому, принимая определенные допущения о стационарности и ординарности потоков в системе, запишем интенсивность перехода Х20 в виде интенсивности упущенного потребления за 5 дней всех товаров, и получим:
^
0 =
А
2
х
х
t%
=
10
х
5
=
50
ед
/
дн
Подставив значения из (8) – (11), в формулы (5), получим:
Р =
0,38
х
0,36
=
0,13
р = — х
0,36
=
0,51
2
50 , ,
^
0
=
70 70 +---1--х 50 50
(50
+
70)
-
1
=
0,36
Таким образом, рассмотренная МСУЗ «минимум - максимум», в целом обеспечивает снабжение клиентов товарами, но предполагает нахождение в состоянии дефицита некоторых товаров с вероятностью Р0 = 0,36. Полученные выражения для вероятностей состояний МСУЗ типа «минимум - максимум» характеризуют ее готовность к обслуживанию клиентов предприятия. Так, если МСУЗ находится в состояниях S1 и S2, то обслуживание клиентов не прекращается, а в состоянии дефицита S0 уровень обслуживания клиентов снижается, так как будет иметь место нехватка хотя бы одного товара из рассматриваемой номенклатурной группы. Таким образом, степень готовности МСУЗ типа «минимум – максимум», для нашего случая, будет характеризоваться таким показателем, как коэффициент готовности к обслуживанию (КГО), который будет равен сумме вероятностей Р1 и Р2, то есть: КГО = Р1 + Р2 = 64 %. (13) При этом предприятие из-за дефицита, в среднем, будет нести убытки в объеме, определяемом по формуле: СД = Р0 × ТR, (14) где, CД – штрафы (потери) из-за дефицита (упущенный доход), тыс. руб.; Р0 – вероятность нахождения МСУЗ в состоянии дефицита, в долях; TR – товарооборот (выручка) торгового предприятия, тыс. руб. Более точные значения упущенного дохода могут быть найдены по зависимости от плотности вероятности нахождения МСУЗ в состоянии дефицита за период Т, например, по формуле: T
C
Д
=
∫
e
-
λ0
⋅
t
⋅
p
t
⋅
dt
=
λ
0
(t)
⋅
eλ0
⋅
t
⋅
p
t
0
=
P0
⋅
TR
0 , (15) λ где, 0 - интенсивность перехода МСУЗ в состояние дефицита, ед./дн.; р t – средний объем продаж за единицу времени, тыс.руб./дн.; Т - период работы МСУЗ, дн.; Р0 – вероятность нахождения МСУЗ в дефиците, в долях (%). TR – товарооборот (выручка) торгового предприятия, тыс. руб. λ
Из формулы (15) следует, что значение 0 равно сумме всех возможных переходов в состояние дефицита. Заметим, что для установившегося режима работы МСУЗ все переходы в состояние дефицита будут составлять определенную долю (или %) от общего времени
Т
работы системы. Кроме того, средняя стоимость продаж в день за весь период работы МСУЗ будет равна или пропорциональна товарообороту (выручке)
TR
в тысячах рублей за год.
Хотя функция затрат является показателем экономической эффективности МСУЗ, однако, она не всегда является определяющей, так как в некоторых случаях через функцию затрат невозможно достаточно полно учесть все факторы, связанные с созданием запасов и возникновением дефицита. Следует заметить, что рассмотренная на рисунке 1 модель МСУЗ типа «минимум - максимум» носит достаточно общий характер, но при необходимости, может уточняться с учетом особенностей управления той или иной номенклатурной группой товаров. Причем, для снижения дефицита может быть эффективно применен аппарат имитационного моделирования, который позволит оптимальным образом подобрать параметры МСУЗ, такие как интенсивности и периоды пополнения запасов. С другой стороны, снижение дефицита и организацию товароснабжения торгового предприятия с минимальными затратами можно добиться за счет разработки и использования перспективных МСУЗ, ориентированных на оптимизацию партий поставки с учетом периодов контроля и доставки. Одной из таких систем может быть МСУЗ «с фиксированными интервалами проверок и пополнением до контрольных уровней» [4]. Для определения возможности применения подобной МСУЗ необходимо закупаемые товары разбить на компонентные группы в рамках конкретной логистической миссии, используя при этом наиболее эффективные методы логистического, например, АВСD - анализ. МСУЗ «с фиксированными интервалами между проверками и подпиткой текущих запасов до контрольных уровней» предполагает формирование оптимальных объемов и периодов пополнения запасов на основе модели Уилсона с учетом коэффициента К, показывающего соотношение затрат на доставку и хранение партий многономенклатурных запасов. Существенным отличием предлагаемой МСУЗ от уже известных является то, что формирование периодов контроля осуществляется на основе теоремы Котельникова-Шеннона, а по результатам контроля проводится подпитка любого вида запаса до контрольного уровня в течение ближайшей совместной плановой поставки любого из номенклатурной группы товаров. Применение предложенного подхода наиболее эффективно для номенклатурных групп, выделенных например, по мощности источников поставки или по грузовместимости транспортных средств доставки, либо в рамках сформированных миссий логистического управления. Модифицированная марковская модель МСУЗ «с фиксированными интервалами между проверками и подпиткой текущих запасов до контрольных уровней» изображена на рис. 2 Рис. 2. Марковская модель МСУЗ «с фиксированными интервалами между проверками и подпиткой текущих запасов до контрольных уровней» На рис. 2 приняты обозначения для данной модели:
–
S1 – исходное состояние МСУЗ, при котором уровни текущих запасов JТЗi n товаров всей номенклатуры пополнены до максимальных значений Jmax или находятся в пределах между максимальным и первым контрольным уровнем, т.е. выполняется условие Jmax i ≤ JТЗ i < J k 1;
–
S2 – состояние МСУЗ, при котором уровень текущего запаса JТЗ i любого из товаров достигает второго контрольного уровня текущего запаса J k 2 и возникает угроза дефицита по наиболее интенсивно потребляемому товару А;
–
S3 – состояние МСУЗ, при котором уровень текущего запаса JТЗ i любого из товаров достигает третьего контрольного уровня текущего запаса J k 3 и возникает угроза дефицита по товарам А и B из номенклатуры с интенсивностью их потребления за время подпитки;
–
S4 – состояние МСУЗ, при котором уровень текущего запаса JТЗ i любого из товаров достигает четвертого контрольного уровня текущего запаса J k 4 и возникает угроза дефицита по товарам С и D из номенклатуры с интенсивностью их потребления за время подпитки;
–
S0 – состояние МСУЗ, при котором уровень текущего запаса любого из номенклатуры товаров может оказаться в дефиците и требует пополнения;
–
µ j,j
– интенсивность перехода МСУЗ из состояния
j
в состояние
i
, соответствующее пополнению или подпитке запаса того или иного товара из
номенклатуры до максимального или контрольного уровня.
-
A
i,j
— интенсивность перехода МСУЗ из состояния
i
в состояние
j
,
соответствующее расходу запаса того или иного товара из номенклатуры до контрольного или минимального уровня. Проведем расчет параметров представленной модели, применяя систему уравнений Колмогорова для СМО c учетом уравнения нормирования.
P
1
Х
(Х 12
+
A
10
)
—
P
0
Х
Н
01
+
P
2
Х
Н
21
Р2 Х
(
X2з + ^20 + Н21) — Р1 Х Х^2 + Р3 Х Ц32
<
Ρ
3
Ρ
4
Х
(
X
34
+
X
30
+
Ц
32
)
—
Р
2
Х
X
23
+
Р
4
Х
Ц
43
Х
(Х40
+
Ц43
)
—
P
3
Х
X34
Ρ Х Ан
—
Р
1
Х
X10
+
P2
Х ^2Q
+
P
3
Х
X
30
+
P
4
Х
X
40
[
Р
0
+
Р
1
+
Р
2
+
Р
3
+
Р
4
—
1
Рассмотрим интенсивности потребленияA i,j с учетом особенностей модели. Интенсивность потребления Х1,2 характеризует переход системы из S1 в состояние S2, соответствующее первому уровню контроля. Это предусматривает периодический контроль расхода всех товаров A, B, C, D одновременно, интенсивность расхода каждого из которых будет равна:
Л
1
= 7^ =
50
=
2,8
ед
/
дн
Л
=
100
=
2,8
ед
/
дн
t П 1 18 ; 2 36 ,
Л
=---=
2,2
ед
/
дн
Л
=---=
2,2
ед
/
дн
3 45 4
;.
Суммарная интенсивность перехода
7
1,2 по всем товарам в течение периода между контрольными проверками, то есть за 9 дней, будет найдена по формуле (8) равна:
\2 =
(2,8
+
2,8
+
2,2
+
2,2)
x
9
=
90
ед/дн.
Интенсивность потребления
Л
2,3 характеризует переход системы из S2 в состояние S3, соответствующее второму уровню контроля. Это предусматривает контроль расхода трех товаров В, С, D одновременно, поэтому она равна сумме интенсивностей расхода товаров в течение 9 дней между очередным контролем:
^ 3 = (2,8 + 2,2 + 2,2) x 9 = 64,8 « 65ед / дн.
Интенсивность потребления
Л
3,4 характеризует переход системы из S3 в состояние S4, соответствующее третьему уровню контроля. Это предусматривает контроль расхода двух товаров C и D одновременно, поэтому она равна сумме интенсивностей расхода товаров за 9 дней:
^
4 =
(2,2
+
2,2)
x
9
=
39,6
«
40
ед
/
дн.
Интенсивность потока
7
10 характеризует переход системы из S1 в состояние S0 дефицита, что маловероятно для любого из материалов A – D, поэтому этот переход носит чисто формальный характер и может считаться равным нулю:
^i о =
0
x
5
=
0
ед
/
дн
Интенсивность потока
7
20 характеризует переход системы из S2 в состояние S0 дефицита в течение периода (5дней) пополнения первого материала A:
Х2 0
=
2,8
x
5
=
14
ед
/
дн
Интенсивность потока
Л
30
, характеризует переход системы из S3 в
состояние S0 дефицита в течение периода (5дней) пополнения второго материала B: ^ п = 2,8 x 5 = 14 ед / дн
3,0
(22)
Интенсивности потоков Л40, характеризует переход системы из S4 в состояние S0 дефицита в течение периода (5 дней) пополнения третьего C и четвертого D материалов:
X
4,0
=
(2,2
+
2,2)
X
5
=
22
ед./дн
Потоки µ j,i будут характеризовать интенсивности потоков пополнения и подпитки материалов. Интенсивность потока µ 2,1 характеризует переход системы из S2 в состояние S1 соответствующее первому уровню контроля. Это предусматривает пополнение товара A:
ц2 x = у = 10
еД/Дн
Интенсивности потоков µ 4,3, µ 3,2 характеризуют переход системы из S4 в состояние S3, а также из S3 в состояние S2, соответствующее 3-му и 2му уровням контроля соответственно. Это предусматривает последовательное пополнение товаров D и C, поэтому они будут равны:
H
4,3
=
H 3,2
= - =
20
5
ед./дн.
Интенсивность потока µ 0,1 характеризует переход системы из S0 в состояние S1, что соответствующее 1-му уровню контроля. Это предусматривает пополнение всех товаров, которые находятся в состоянии дефицита, поэтому она в предельном случае будет равна сумме интенсивностей пополнения всех товаров 50 100 100350 H 01 = —+ + == 5 5 5 5 ед/дн(26) Подставим полученные значения из (17) - (26) в систему уравнений (16), в состав которой включим нормировочное уравнение, и получим:
'P
x
90
=
Po
x
70
+
P2
x
10
P2
x
(
90
+
14
+
10
)
=
Pj
x
90
+
P3
x
20
P3
x
(
90
+
14
+
20
)
=
P2
x
90
+
P4
x
20
'
P4
x
(22
+
20)
=
P3
x
90
[
Р
0
+
Р
1
+
Р
2
+
Р
3
+
Р
4
=
1
Упростим цифровые значения в системе (27):
'P
=
0,78
x
Po
+
0,11
x
P2
P2
=
0,79
x
Pj
+
0.18
x
P3
P3
=
0,79
x
P2
+
0,18
x
P4
> 4 = 2,13 x P3
[
Р
0
+
Р
1
+
Р
2
+
Р
3
+
Р
4
=
1
В итоге вероятности состояний будут равны: Р0 = 0,1; Р1 = 0,1; Р2 = 0,16; Р3 = 0,2; Р4 = 0,44. Таким образом, МСУЗ будет находиться в состоянии S0 дефицита 10 % времени в течение периода функционирования, то есть в течение 36 дней в год (при ТГОД = 360 дней), или в течение 9 дней в квартал (при ТКВ = 90 дней). Согласно формуле (14) при объеме квартальной выручки, равной 927,34 тысячи рублей (табл. 1), потери от упущенных продаж при использовании МСУЗ «с фиксированными интервалами проверок и пополнения до контрольных уровней» в среднем могли бы составить:
Dw
=
0,1
x
TR
=
0,1
x
272,34
=
27,234(
тыс
.
руб.)
Это на 26% или на 304026 рублей меньше, чем при использовании МСУЗ типа «минимум – максимум». Состояние Р0 соответствует состоянию МСУЗ при дефиците по любому из товаров. Вероятности состояний Р1, Р2, Р3, Р4 характеризуют бездефицитные состояния МСУЗ и возможность обслуживания клиентов по любому виду товаров, тогда коэффициент готовности к обслуживанию согласно (13) будет равен: КГО = Р1 +Р2 +Р3 +Р4 = 90% Полученный результат показывает, что применение МСУЗ «с фиксированными интервалами проверок и пополнения до контрольных уровней» может сократить долю упущенных продаж и повысить коэффициент готовности МСУЗ к обслуживанию на 26%. Таким образом, нами рассмотрены варианты марковских моделей функционирования МСУЗ типа «минимум-максимум» и МСУЗ «с фиксированными интервалами проверок и пополнения до контрольных уровней», которые позволяют определять уровни упущенных продаж от возникновения дефицита и коэффициент готовности системы управления запасами к обслуживанию клиентов. Применяемая на торговом предприятии МСУЗ типа ««минимум- максимум», обеспечивает ее готовность к обслуживанию клиентов на 64%, однако, может приводить к потере выручки на 36% , за счет упущенных продаж. Этот показатель подтверждается анализом продаж предприятия, проведенным за 3 квартал 2014 года. Наиболее выгодным инновационным проектом для предприятия, может стать внедрение МСУЗ «с фиксированными интервалами проверок и пополнения до контрольных уровней», которая обеспечивает ее готовность к обслуживанию клиентов на 90% и снижает потери выручки от упущенных продаж на 26%. Дальнейшие исследования в этом направлении могут быть направлены на разработку новых марковских и полумарковских моделей для типовых видов СУЗ и дальнейшее совершенствование предложенных моделей. Применение предложенного подхода к оценке готовности СУЗ к обслуживанию клиентов наиболее эффективно для номенклатурных групп, выделенных, например, по мощности источников поставки или по грузовместимости транспортных средств доставки, либо в рамках сформированных логистических миссий управления.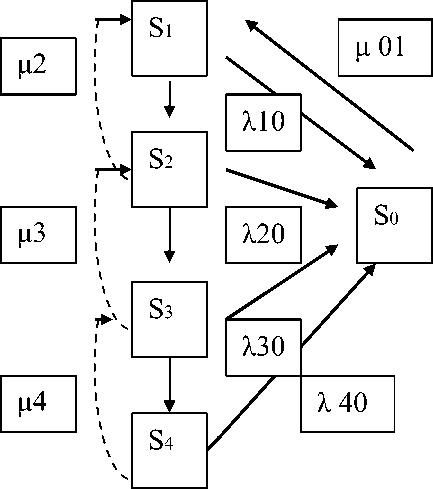
Список литературы Совершенствование многономенклатурных систем управления запасами в торговле аннотация
- Аникин Б.А. Логистика: учеб. пособие/под ред. Б.А. Аникин, Т.А. Родкиной. -М.: ТК Велби, Изд-во Проспект, 2008.
- Гаджинский А.М. Логистика: Учебник. -14-е изд., перераб. и доп. -М.: Издательско-торговая корпорация «Дашков и К˚», 2007.
- Голик Е.С. Математические методы системного анализа и теории принятия решений. Ч. 2. -М. С-Пб, 2006.
- Силин А.В. Оптимизация периодов контроля в логистических системах управления запасами на основе теоремы Котельникова.//Современная торговля: теория, практика, инновации: Материалы IV всероссийской научно-практической конференции с международным участием (Пермь, 21-23 ноября 2011 г.). Том 1/ПИ (Ф) ФГБОУ ВПО РГТЭУ. -Пермь: изд. «ОТ и ДО», 2011.


