Совершенствование неразрушающего метода определения механических характеристик элементов многослойных конструкций на примере дорожных одежд

Многослойные среды находят широкое распространение в инженерной и строительной практике. Одним из часто встречающихся видов многослойных сред являются дорожные одежды на автомобильных дорогах. Дорожная одежда – один из наиболее ответственных и дорогостоящих элементов автомобильной дороги, призванных обеспечить как комфорт движения и безопасность пользователей автомобильной дороги, так и ее долговечность в пределах всего расчетного срока службы. Как правило, они включают в себя слои асфальтобетонного покрытия, слои основания, обработанного или не обработанного вяжущими материалами, а также слои из инертных материалов, выполняющие функции дополнительного слоя или рабочей зоны грунта земляного полотна. При деформировании слои дорожной одежды проявляют достаточно широкий спектр свойств, объединяющий механизмы упругого и вязкоупругого деформирования, что приводит к сложностям при оценке их состояния на этапе эксплуатации [1–3].

На данный момент основным методом неразрушающего контроля, применяемым на стадии эксплуатации и позволяющим оценить жесткостные свойства отдельных элементов, является метод «обратного» расчета, базирующийся на решении обратной коэффициентной задачи восстановления модулей упругости по замеренной в полевых условиях чаше упругих прогибов [4–8]. Данный подход имеет как серьезные достоинства, определившие его широкое внедрение в мировой практике, но вместе с тем и определенные недостатки, связанные с некоторой идеализацией исследуемых сред. Главным достоинством данного метода является возможность получения конкретных расчетных механических параметров слоев дорожной конструкции, которые в дальнейшем могут быть использованы для принятия проектных решений и расчетов усиления конструкций в рамках капитального ремонта [9–11]. К недостаткам можно отнести применение достаточно сложного математического аппарата и неоднозначность способов преодоления некорректности задачи. К таким способам можно отнести численные итерационные методы типа

Ньютона, Левенберга – Марквардта, генетические алгоритмы [12–15]. В виде отдельного научного направления в последние годы выделилось применение искусственных нейронных сетей [16–19], однако здесь первоочередной проблемой является адекватность и полнота данных, на которых происходит их обучение. Поэтому, резюмируя вышесказанное, следует отметить, что, на наш взгляд, дальнейшее развитие данного класса методов должно базироваться на более полном учете физической природы механизмов деформирования конструктивных слоев под воздействием нагрузок. Это приводит к заключению, что наряду с модулями упругости очевидна необходимость восстановления и параметров потерь энергии деформирования [20–23], что в рамках реализованных на данный момент методов не представляется возможным. Исходя из этого целью данной работы является разработка метода определения параметров упругости и потерь отдельных конструктивных слоев дорожных одежд, по замеренным в полевых условиях петлях динамического гистерезиса.

1. Методы

Энергетический баланс в упругой многослойной среде может быть представлен в следующем виде [24; 25]:

W = W ν , z + W R , z

где W – общий поток энергии, закачиваемой в cреду; W _{ν , z} – энергия, уносимая от источника колебаний продольными волнами и волнами сдвига; W _{R , z} – энергия, уносимая волнами Рэлея на бесконечность.

Величина потока энергии продольных и поперечных волн может быть определена в соответствии со следующим соотношениями:

В свою очередь энергия потерь W _loss с позиции анализа экспериментальных данных распадается на отдельные составляющие и может быть представлена в виде:

W, = w +W + W loss вязк разр темп , где Wвязк – величина энергии потерь, затрачиваемая на вязкоупругое деформирование материала; Wразр – величина энергии потерь, рассеиваемая при различных аномалиях дефектах и разрушениях в теле материала; Wтемп – энергия, необратимо рассеянная в пространстве в виде тепла.

Таким образом, можно заключить, что величина энергии потерь однозначно характеризует структурные свойства всей конструкции в целом и отдельных элементов ее конструктивных слоев и является эффективным индикатором состояния слоистой конструкции.

С практической точки зрения учет энергии потерь при деформировании многослойной конструкции может быть полезен при решении задачи восстановления характеристик слоев многослойной дорожной конструкции неразрушающим методом. Так, стандартная постановка обратной коэффициентной задачи о минимизации функционала minΦ(Ej)=min∑ Uэксп(Ri)-Uрасч(Ej,Ri)2 (6) i может быть дополнена требованием минимума функционала minW *:

W * = min

t

∑∫ i0

эксп σ

( R 0 ) £ эк™ ( R i ) dt - J а расч ( R 0 ) £^расч

( R i ) dt , (7)

w

ν , z

χ

=-      Im R ( α , 0) | Q 3 ( α ) | 2 α d α ,

4π

W R , z =-^ω 4 r e sR ( α ,0)| α=ξ | Q 3 ( ξ )|² ξ ;         (3)

где R ( α ,0 ) – функция, входящая в состав символа-матрицы Грина, построенной для упругого полупространства [25]; Q ₃ – Фурье-образ вертикальной компоненты нагружения на поверхности многослойной среды; ω – круговая частота; χ – верхний предел зоны комплекснозначности; α , ζ – Фурье-образы координаты движения поверхностной нагрузки.

Вместе с тем для случая многослойного вязкоупругого полупространства зависимость (1) может быть представлена в виде:

W = W ν , z + W R , z + W loss              (4)

где W _loss – величина энергии потерь, связанная с проявлением вязких свойств конструктивных слоев многослойной конструкции.

где U ^эксп ( R _i ) – функция, описывающая форму чаши упругих прогибов на поверхности многослойной среды, зарегистрированных на расстояниях R i от точки приложения ударной нагрузки; U ^расч ( E _i , R _i ) – функция, описывающая зависимость расчетных значений упругих прогибов от значений модулей упругости конструктивных слоев многослойно среды, строящаяся с использованием математической модели динамического НДС; R 0 – центр приложения нагрузки; σ эксп , ε эксп – напряжения и деформации поверхности дорожной конструкции, регистрируемые при экспериментальном нагружении; σ расч , ε расч – напряжения и деформации поверхности дорожной конструкции, рассчитываемые с использованием математической модели.

Итоговый вид минимизируемого функционала соответствует аналогу процесса регуляризации по Тихонову и можно записать следующим образом:

M = Φ+λ W *, (8)

где λ – параметр регуляризации.

Построение зависимостей вида ст ^расч ( е ^расч) для случая определения НДС многослойного вязкоупругого полупространства затруднительно, в связи с отсутствием нормированных параметров затухания как отдельных слоев дорожной конструкции, так и ее в целом. Таким образом, в отличие от модулей упругости, где точка отсчета в виде начальных значений модулей упругости, на основе которых строится расчетная чаша прогибов, существует, здесь – отсутствует. Однако применение современного измерительного оборудования в виде установок динамического нагружения с падающим грузом позволяет осуществлять регистрацию динамических петель гистерезиса на поверхности дорожной одежды в координатах «нагрузка ( F ) – перемещение (u)» F ^эксп ( u ^эксп) [26; 27]. Площади, зарегистрированных таким образом петель гистерезиса, служат аналогом величины диссипации энергии на удалении от точки приложения нагрузки.

В расчетной модели представляется возможным аналогичное представление F ^расч ( u ^расч) путем наложения расчетного импульса силы F ( t ), подчиняющегося синусоидальному закону на амплитудно-временную характеристику деформирования на поверхности многослойной среды u ( R , t ):

I F 0 .;_( П t V

I м2 sin I I , t ^{G [0} , t имп ^] ; /ГГ1 F ⁽ t ) 'п R ² ( t имп J ⁽⁹⁾

[c, t 4 [0, tимп ], где F0 – усилие на поверхности конструкции, распределенное по пятну контакта радиуcом R; tимп – время импульса (tимп =30 мс).

Форма амплитудно-временной характеристики перемещений может быть получена путем разложения функции внешней нагрузки F ( t ) во временной ряд Фурье;

M

• ^{u ( R} , t ) = s p k ( ^- cos ^{n im} i ^uR , . ex i. k t , ] . (10) + sin n _k Re [ u ( R , to _k )exp( - i to k t ) ] } ,

• 2. Результаты

  Инструментальные исследования были проведены на участке автомобильной дороги М4 «ДОН» км 933– 1024. Конструкция дорожной одежды на обследованных

где p _k – коэффициенты разложения импульса ударного нагружения в ряд Фурье; to _k - набор круговых частот, определяемый исходя из параметров импульса приложения нагрузки; n k - параметр фазового сдвига, определяемый исходя из набора круговых частот to k .

Более подробно механизм решения задачи об определении динамического НДС многослойной среды изложен в работах [28–30]. В качестве меры диссипации энергии в данной статье будет использоваться тангенс угла потерь энергии tg ф .

участках включала в себя слои асфальтобетона толщиной 20–35 см, слои основания из неукрепленной вяжущим щебеночно-песчаной смеси толщиной 30–40 см и грунта земляного полотна. Помимо представленной конструкции на локальных участках встречались слои из щебеночно-песчаной смеси, укрепленной цементом, толщиной 15–24 см. В рамках данной статьи рассмотрены два варианта конструкции дорожной одежды, содержащей слой основания, укрепленный цементом, и со слоем основания, не обработанным вяжущим (табл. 1).

Таблица 1

Конструкция дорожной одежды на опытных участках

Тable 1

Construction of pavement on experimental sites

Конструкция дорожной одежды с неукрепленным основанием	Толщина слоя, см	Конструкция дорожной одежды с укрепленным основанием	Толщина слоя
Асфальтобетон	34	Асфальтобетон	17
Щебеночнопесчаная смесь	35	Щебеночно-песчаная смесь, укрепленная цементом	17
Грунт – глина	-	Щебеночно-песчаная смесь	41
		Грунт	-

Экспериментальные измерения чаш упругих прогибов осуществлялись с использованием установки динамического нагружения с падающим грузом FWD PRIMAX 1500, оснащенной комплектом датчиков-геофонов для регистрации чаш упругих прогибов1.

Экспериментальные чаши упругих прогибов, зарегистрированные на данных участках, а также расчетные (построенные в программном комплексе АЭМ) представлены на рис. 1.

Результаты расчета динамических модулей упругости представлены в табл. 2.

Также были экспериментально зарегистрированы (рис. 2) и построены с использованием математической модели петли гистерезиса для каждого из датчиков установку динамического нагружения с падающим грузом (рис. 3).

Как видно из представленных рисунков, при схожем форм-факторе расчетных и экспериментальных петель динамического гистерезиса присутствует отличие в величине их площади. Это наглядно продемонстрировано в табл. 3, в которой приведено сопоставление расчетных и экспериментальных площадей петель гистерезиса. Так как площадь петли гистерезиса определя- ется процессами диссипации энергии в структуре дорожной одежды была произведена итоговая корректировка значений тангенсов углов потерь в слоях дорожных конструкций для минимизации отклонений площадей петель гистерезиса (табл. 4).

Результаты корректировки в виде расчетных петель динамического гистерезиса приведены на рис. 4. Итоговые значения модулей упругости слоев дорожной одежды и тангенсов углов потерь энергии в конструктивных слоях приведены в табл. 5.

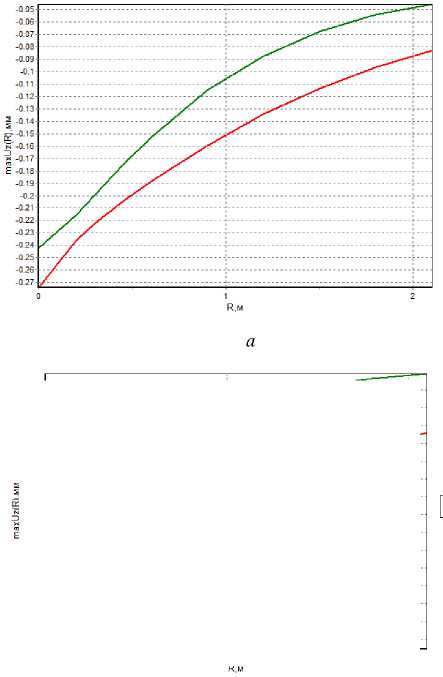
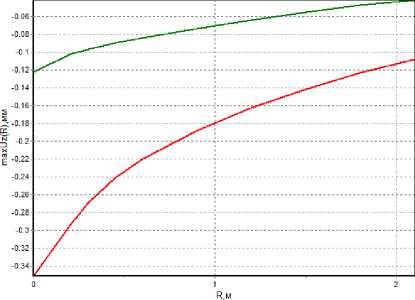
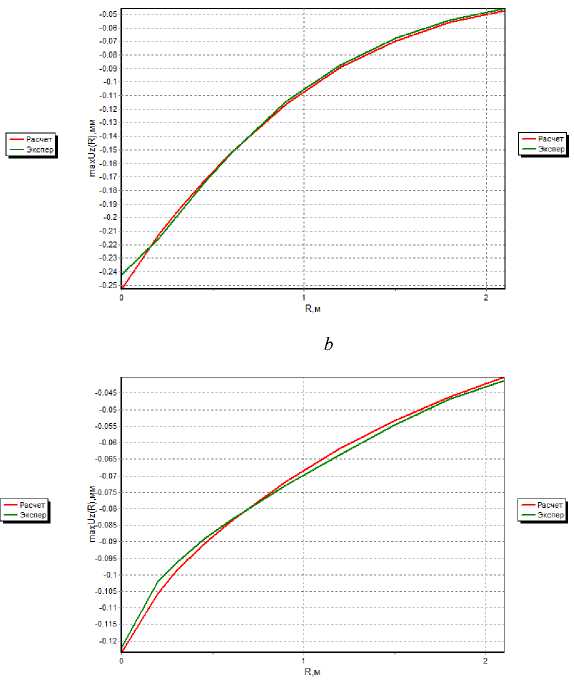
Рис. 1. Расчетные и экспериментальные чаши прогибов до и после корректировки ( а , b – для дорожной одежды с неукрепленным основанием соответственно; c , d – с укрепленным)

d

Fig. 1. Calculated and experimental bowls of deflections before and after adjustment ( a , b – for pavement with unreinforced base, respectively; c , d – with reinforced)

Таблица 2

Значения модулей упругости конструктивных слоев дорожных одежд после корректировки

Table 2

Values of modulus of elasticity of structural layers of pavements after adjustment

Конструкция дорожной одежды с неукрепленным основанием	Динамический модуль упругости, МПа	Конструкция дорожной одежды с укрепленным основанием	Динамический модуль упругости, МПа
Асфальтобетон	2870	Асфальтобетон	6400
Щебеночно-песчаная смесь	80	Щебеночно-песчаная смесь, укрепленная цементом	5000
Грунт – глина	120	Щебеночно-песчаная смесь	600
		Грунт	150

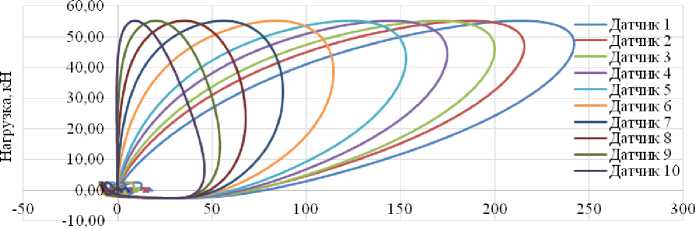
Вертикальные деформации, мкм

а

b

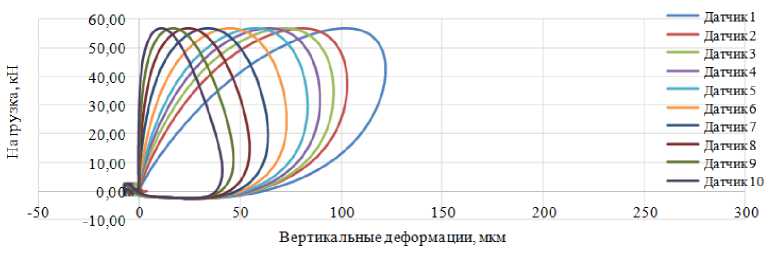
Рис. 2. Экспериментальные петли динамического гистерезиса, зарегистрированные на участках автомобильной дороги с неукрепленным ( а ) и укрепленным ( b ) основанием

Fig. 2. Experimental dynamic hysteresis loops recorded in the areas road with unreinforced and reinforced base

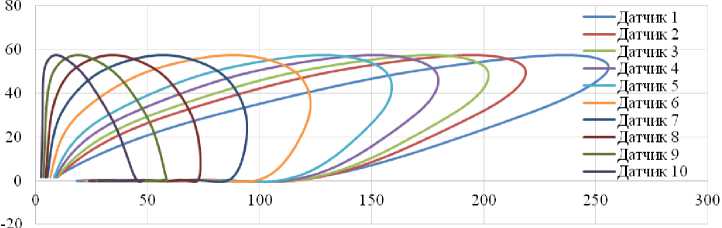
a

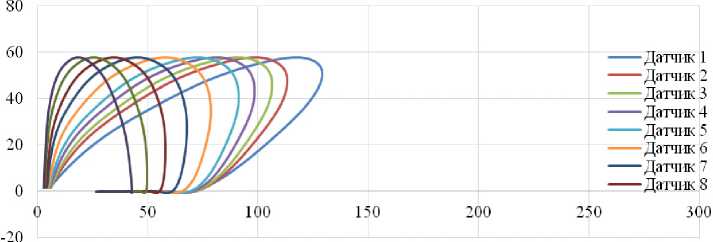
b

Рис. 3. Расчетные петли динамического гистерезиса, зарегистрированные на участках автомобильной дороги с неукрепленным ( а ) и укрепленным ( b ) основанием

Fig. 3. Calculated dynamic hysteresis loops recorded in sections of the automobile roads with unfortified ( a ) and fortified ( b ) base

Table 3

Experimental and calculated areas of hysteresis loops, and the magnitude of deviations between them

Датчик	D1	D2	D3	D4	D5	D6	D7	D8	D9	D10
Конструкция 1 – диссипация энергии по датчику, Дж/м3
Эксперимент	7,28	6,78	6,60	6,09	5,60	4,70	3,95	3,23	2,59	2,02
Расчетные значения	4,88	4,87	4,83	4,73	4,61	4,28	3,85	3,37	2,86	2,35
Отклонение	-0,49	-0,39	-0,37	-0,29	-0,21	-0,10	-0,02	0,04	0,09	0,14
Конструкция 2
Эксперимент	4,40	4,05	3,95	3,79	3,62	3,32	2,98	2,58	2,19	1,85
Расчетные значения	3,76	3,74	3,72	3,67	3,61	3,44	3,22	2,95	2,65	2,32
Отклонение	-0,17	-0,08	-0,06	-0,03	0,00	0,04	0,08	0,12	0,17	0,20

Table 4

Results of Comparison of the Total Areas of Calculated and Experimental Hysteresis Loops

Датчик	D1 {	D2 {	D3 {	D4 {	D5 {	D6 {	D7 {	D8 {	D9 {	D10
Конструкция 2 – диссипация энергии по датчику, Дж/м3
Эксперимент	7,28	6,78	6,60	6,09	5,60	4,70	3,95	3,23	2,59	2,02
Расчетные значения	6,88	6,27	5,99	5,61	5,24	4,54	3,90	3,30	2,74	2,25
Отклонение	-0,06	-0,08	-0,10	-0,09	-0,07	-0,03	-0,01	0,02	0,05	0,10
Конструкция 2 – диссипация энергии по датчику, Дж/м3
Эксперимент	4,40	4,05	3,95	3,79	3,62	3,32	2,98	2,58	2,19	1,85
Расчетные значения	4,12	3,79	3,66	3,51	3,37	3,10	2,84	2,57	2,29	2,01
Отклонение	-0,07	-0,07	-0,08	-0,08	-0,07	-0,07	-0,05	0,00	0,04	0,08

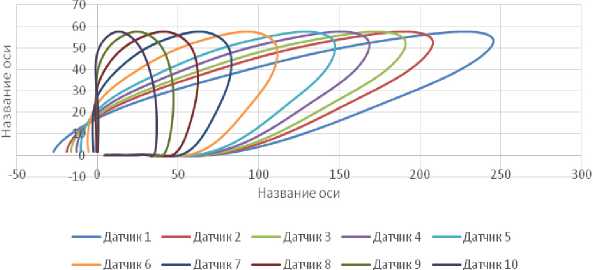
а

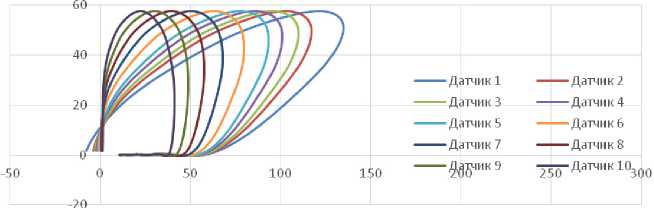
b

Рис. 4. Расчетные петли динамического гистерезиса, зарегистрированные на участках автомобильной дороги с неукрепленным ( а ) и укрепленным ( b ) основанием, откорректированные с учетом диссипации энергии в дорожной конструкции

Fig. 4. Calculated dynamic hysteresis loops recorded on sections of the road with unreinforced ( a ) and reinforced ( b ) bases, corrected for energy dissipation in the road structure

Таблица 5

Итоговые результаты расчета модулей упругости и тангенсов углов потерь с учетом корректировки расчетных чаш прогибов и петель гистерезиса

The final results of the calculation of the elastic moduli and loss tangents, taking into account the correction of the calculated deflection bowls and hysteresis loops

Table 5

Конструкция дорожной одежды с неукрепленным основанием	Модуль упругости, МПа	Тангенс угла потерь	Конструкция дорожной одежды с укрепленным основанием	Модуль упругости, МПа	Тангенс угла потерь
Асфальтобетон	3170	0.86	Асфальтобетон	7400	0.91
Щебеночно-песчаная смесь	80	0.73	Щебеночно-песчаная смесь, укрепленная цементом	5000	0.80
Грунт – глина	170	0.75	Щебеночно-песчаная смесь	600	0.80
			Грунт	160	0.82

В ходе корректировки было установлено, что значения модулей упругости слоев дорожной одежды и тангенсов углов потерь в них оказывают комплексное влияние на площади динамических петель гистерезиса и характера затухания энергии на удалении от точки приложения нагрузки. При этом в наибольшей степени на площадь динамических петель гистерезиса влияние оказывает модуль упругости подстилающего полупространства, не ограниченного по толщине, а уменьшение рассеиваемой энергии на удалении от точки приложения нагрузки связано, в первую очередь, с тангенсами углов потерь энергии в слоях полупространства, принимающих значения, указанные в табл. 5. При этом, очевидно, дискуссионным является представление о том, что данные значения тангенсов углов потерь характеризуют исключительно вязкость материала, так как полученные значения достаточно велики, чтобы характеризовать мнимую составляющую комплексного модуля упругости материала. Основным объяснением получаемых значений служит то, что они учитывают закономерности рассеяния энергии на границах контактирующих слоев дорожной одежды, а также возможные аномалии и расслоения в рассчитываемых конструкциях. Как видно из представленных результатов корректировки, расчетная картина затухания энергии на удалении от точки приложения нагрузки практически полностью соответствует экспериментальной, не отклоняясь ни по одному из датчиков на величину более 10 %.

Заключение

Представлены результаты совершенствования метода неразрушающего контроля состояния конструктивных слоев нежестких дорожных одежд, основанного на решении «обратной» задачи, в части учета их вязко