Совершенствование определения коэффициента интенсивности напряжений методом малобазной тензометрии

При расчетах срока службы и надежности элементов металлических конструкций с применением параметров механики разрушения требуется знание выражения для определения коэффициента интенсивности напряжений (КИН) для элементов различной формы, отличающихся схемой приложения нагрузок и содержащих трещины произвольной ориентации.

Прогнозирование распространения усталостной трещины, основанное на концепции силового параметра механики разрушения – КИН, полученного при анализе упругих напряжений у неподвижной трещины при статическом нагружении, предполагает, что КИН сохраняет свое значение лишь тогда, когда пластическая зона мала. То есть условия локального пластического деформирования в вершине трещины определены для упругопластического тела с неподвижной трещиной подвергнутого статическому нагружению такой нагрузкой, при которой пластическая зона в вершине трещины локализуется внутри области, в которой упругие сингулярные поля доминируют [1]. В этом случае КИН является параметром поля напряжений, который включает эффекты схемы нагружения, геометрии и размера трещины и предполагает однозначный контроль размера пластики в вершине трещины.

В работе [2] была реализована методика определения КИН тензометрическим методом с использованием цепочек 2-компонентных тензорезисторов с базой 0,5 мм, обеспечивающими высокую чувствительность и широкий измерительный диапазон в окрестности вершины трещины. Однако в данной методике при вычислении напряжений игнориро- валось наличие в вершине усталостной трещины зон пластических деформаций и остаточных сжимающих напряжений, сформировавшихся при разгрузке в ее окрестности (величина и распределение которых неизвестны), различия в закономерностях деформирования материала в пределах циклической пластической зоны (проявляется эффект Баушингера) и вне ее.

В работах [3, 4] установлено, что выражения линейной механики разрушения применимы для вычислений АКI, поскольку размер циклической пластической зоны впереди фронта трещины Агц во много раз меньше ее длины Агц << l и интенсивность циклических пластических деформаций полностью контролируется AKI, а распределение размаха напряжений Асту за пределами зоны Агц описывается асимптотическими выражениями а^=А^(6) - (1)

V 2п r где AKI - размах коэффициента интенсивности напряжений; fij (9) - тригонометрические функции от угла 9 ; 9 - угол между плоскостью трещины и радиусом вектором; при 9 = 0, fj (9) = 1.

Это позволяет скорректировать тензометрический метод определения КИН: использовать предлагаемую в [2] методику для определения размаха КИН. В качестве примера на рис. 1 приведены эпюры распределения размахов деформаций Ае у ( r ), Ае х ( r ) и нормальных напряжений Аст у ( r )

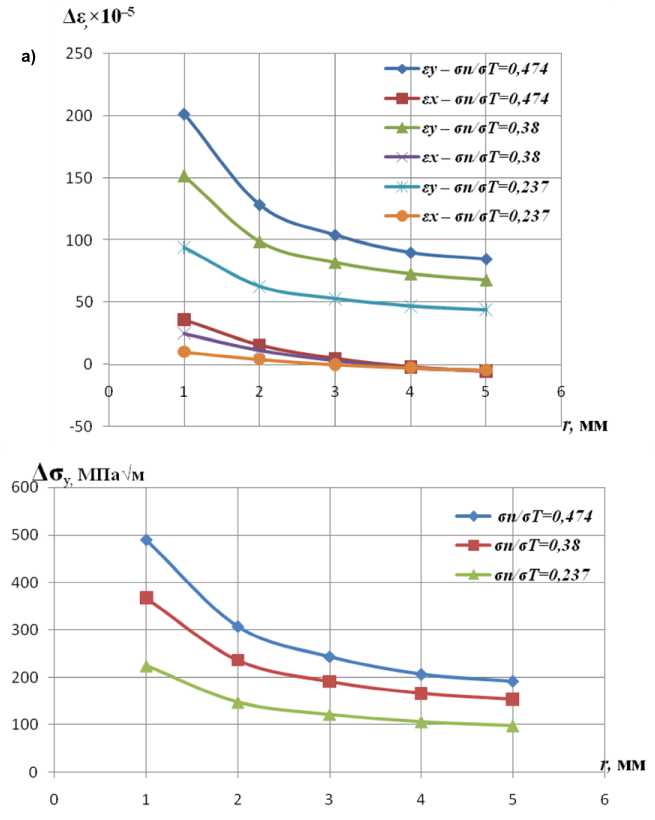
Рис. 1. Распределение размахов деформаций (а) и напряжений (б) перед вершиной трещины

в направлении продолжения трещины в образце на центральное растяжение (ЦР). Образец был изготовлен из стали 09Г2С. Переход от измеренных деформаций к напряжениям осуществлялся с использованием циклической диаграммы деформирования стали 09Г2С.

Экспериментальные зависимости Ас у (r), по лученные при различных уровнях номинальных напряжений и относительных длинах трещины l[W , были использованы для определения AKI по выражению (1) при 0 = 0, fj (0) = 1.

На рис. 2 экспериментально полученные значения размаха КИН сопоставлены с вычисленными по формуле

A K = Ac n п lsec ( п l)w ) .                   (2)

Видно, что имеет место хорошее соответствие сравниваемых значений.

Данный подход был применен для экспериментального определения КИН для сварных на- хлесточных соединений из двух спаренных уголков, изготовленных из стали С390.

Испытания проводили в следующей последовательности. После достижения усталостной трещиной относительной длины l W = 0,15; 0,25; 0,3; 0,5 при циклическом нагружении с уровнем напряжений с n js _т = 0,23; 0,26 в сварных нахлесточных соединениях из двух спаренных уголков испытательную машину останавливали. Наклеивали непосредственно перед вершиной трещины в направлении траектории ее развития миниатюрные многокомпонентные цепочки фольговых тензоре-зисторов с базой 0,5 мм.

Затем к узлам прикладывали повторностатическую нагрузку (с заданным уровнем номинальных напряжений и коэффициентом асимметрии цикла R по нагрузке) и измеряли деформации у вершин трещины. После измерений соединения подвергали циклическому нагружению до момента достижения трещиной следующей величины относительной длины. Последовательное повторение

Теория расчета строительных конструкций

указанных операций позволило в процессе испытания соединений получить экспериментальные зависимости Ле у = f ( r ) (рис. 3) и Ла у = f ( r ) (рис. 4), вычислить размах КИН для испытанных соединений при различных относительных длинах трещины и определить функцию f _{1 k} (рис. 5).

напряжений и относительных длинах трещины l]W , были использованы для определения Л К ₁ следующим образом. В наиболее общем виде выражение для Л К ₁ для сквозных трещин можно записать:

Л К = Ла nJl f i k ,

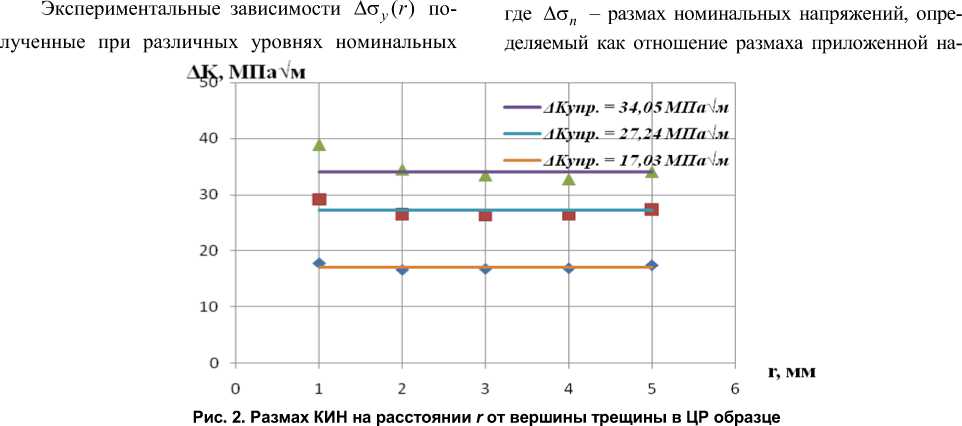
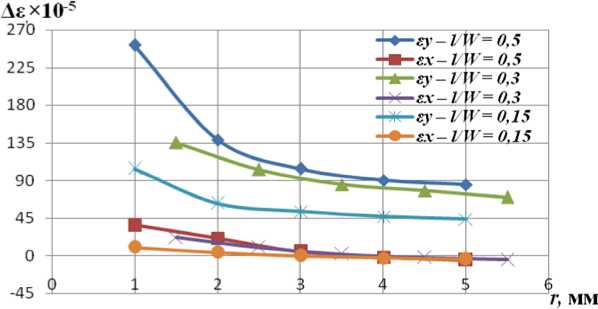
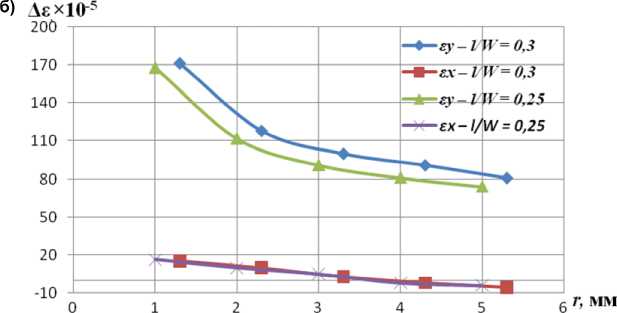
Рис. 3. Распределение размахов деформаций в вершине трещины в сварных нахлесточных соединениях из двух спаренных уголков при различных относительных длинах l W и уровнях нагружения:

а) Ла n /а _т = 0,23; б) Ла n /а _т = 0,26

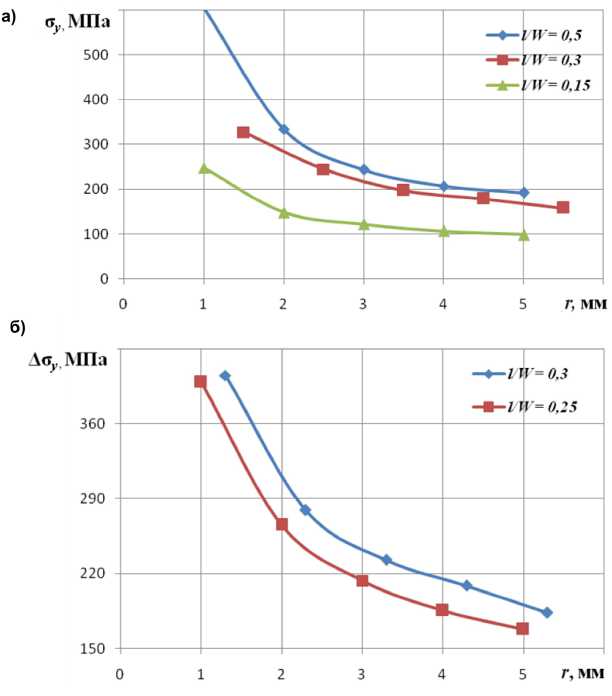
Рис. 4. Распределение размахов напряжений в вершине трещины в сварных нахлесточных соединениях из двух спаренных уголков при различных относительных длинах l W и уровнях нагружения: а) До n ^5 _т = 0,23; б) Да n /а _т = 0,26

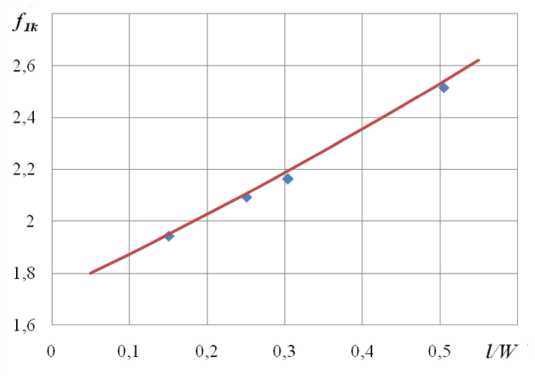
Рис. 5. Зависимость f _{1 k} от относительной длины трещины l W

грузки к площади сечения брутто; l – половина длины трещины; f _{1 k} – функция, характеризующая схему нагружения, форму и конечные размеры элемента с трещиной. Приравнивая (3) и (1), выразим f _{1 k} :

/ 1 к = [^До у V²^/ ^До n ^ ] r ¹² . (4)

Следует отметить, что для указанных разма-хов номинальных напряжений и относительных длин трещин, распределение размахов напряжений на значительном участке в окрестности вершины трещины описывается КИН. Границы участка Д г ц min и Д г ц max , в пределах которого асимптотическое выражение линейной механики разрушения

Теория расчета строительных конструкций

вполне согласуется с полученными экспериментальными данными, достигали значений: 0,013^0,038 < А г ц /I < 0,1 ^ 0,173, что для испытанных соединений составило примерно от 1 до 7 мм.

Экспериментально полученные значения f1k были аппроксимированы зависимостью fk = 1,7282 +1,415| — 1 + 0,3836(—)2.    (5)

• ^{1    k}                  I w J            w

Как видно из рис. 5, аппроксимирующая кривая хорошо согласуется с экспериментальными данными, полученными при испытании сварных нахлесточных соединений.