Совершенствование организации производства на текстильных предприятиях Азербайджана на основе ресурсосбережения

Наряду с экономическими требованиями к эффективности производства данных изделий государственным заказом устанавливаются повышенные требования к качеству изделий, прежде всего, к показателям формоустойчивости, вытекающие из особых условий эксплуатации одежды этого вида. В настоящее время из-за применения нерациональных технологических процессов и организационных решений эти требования часто не выполняются. В связи с этим возникает проблема проектирования экономических технологических процессов, обеспечения выполнения требований по качеству. В рамках этой проблемы актуальным является разработка методики количественной оценки прогнозирования значений показателей качества, в частности, формоустойчивости деталей, узлов и изделия в целом.

В известных работах по проблемам повышения эффективности швейного производства задачи выбора конструкции изделий, проектирование изолированно. При несомненном научно-методическом и практическом значении этих работ, они оставляли неиспользованным дополнительный резерв повышения эффективности швейного производства, связанный с комплексным рассмотрением организационных и технологических факторов в рамках единой оптимизационной модели. Целью работы является исследование и решение важной для народного хозяйства Азербайджана проблемы, связанной с повышением эффективности использования трудовых и материальных ресурсов при изготовлении одежды стабильного ассортимента, удовлетворяющей повышенным требованиям по качеству, на основе комплексной оптимизации организационнотехнологической подготовки производства с использованием многокритериальных моделей и методов динамического и стохастического программирования.

Многовариантная технологическая последовательность изготовления кителя предусматривает до 3 ²⁸ вариантов изготовления изделий. Разница между самым дорогим и дешевым вариантом составляет ~ 30 руб., а самым производительным и непроизводительным вариантом – 3000

сек. Реализация наиболее производительного варианта в условиях предприятия на данном этапе неприемлема, т.к. не обеспечивает требуемого уровня прибыли.

При этом трудно «сходу» выбрать такие операции, свойства которых гарантировали бы получение указанной прибыли при требуемой производительности. Вместе с тем принципы оптимизации технологического процесса, обеспечивающие получение необходимой прибыли при запланированных затратах времени, достаточно очевидны.

Если оптимизировать процесс с целью получения максимальной прибыли, то оптимальную стратегию можно записать в виде:

С →min ⌈Т⌉ где С – себестоимость изделия;

T – затраты времени на изготовление изделия;

[Т] – нормативные затраты времени.

Если основной целью является минимизация затрат времени на изготовление изделия, то оптимальная стратегия будет иметь вид:

Т→ min

С≤⌈ С ⌉

Задача оптимизации технологического процесса для изготовления одежды стабильного ассортимента может быть также сведена к рациональному комплексу между величинами С и Т при установленном уровне оптовых цен на сырье, материалы, оборудование и т. д.

Вышеприведенный анализ позволяет сделать заключение о возможности в рамках срока действия стандарта варьирования в достаточно широких приделах конструктивных решений деталей, узлов изделия, методов их обработки, используемого оборудования в применяемых материалов без ухудшения функциональных свойств изделий.

На базе такого варьирования может быть генерировано множество рациональных вариантов изготовления одежды ста- бильного ассортимента, допустимых с точки зрения обеспечения требуемого ее на изготовление, как правило, являются дискретно – убывающей функцией, т. е. самый дешевый вариант изготовления полочки (вариант 3) является наиболее трудоемким и наоборот (вариант I).

C 3 = C min =159,4 руб.

T 3 =T max = 0,010 ч.

C 1 =C max = 195,4 руб.

T 1 =T min = 0,008 ч.

Аналогичная картина получается и для технологического процесса изготовления изделия в целом, функция С (Т) также носит характер дискретно – убывающий зависимости между суммарной стоимостью и затратами времени.

Решение такой задачи рассматривается как процесс последовательного получения частных решений по конкретным значениям некоторых параметров.

С учетом этого достижение сформулированной цели по минимизации материальных и трудовых затрат на обмундирование в работе обеспечивается последовательным выполнением определённого комплекса мероприятий, обуславливаемого спецификой производства этого обмундирования и предъявляемым к нему требованиям. Минимизация некоторого показателя, в частности критерия затрат W на производство заданных видов одежды в требуемых количествах, является генеральной целью, а математическое выражение для критерия W – целевой функцией.

В соответствии с классификацией, представленной ранее, все изделия, поставляемые для нужд страны, подразделяются на i -е виды ( i = I, 2, ... , m ). Производство изделий распределяется на j потокам (j = I, 2, ... , n) . Существует принципиальная возможность изготовления каждого из i- ых видов изделия на каждом из j-ых потоков.

Одновременно с этим каждый из i-ых видов изделий изготовляется последовательным выполнением R-го числа технологических операций (R = I, 2, ..., K). При этом существует принципиальная возможность варьирования (в условиях обес- печения функциональных требований) материалами и конструкцией узлов и деталей изделия, режимами (способами) их обработки и применяемыми с этой целью средствами (оборудованием, оснасткой, транспортирующими устройствами и т.п.). Таким образом, имеет принципиальная возможность изготовления каждого i-го вида изделия на j-ом потоке R-ым числом операций, каждая из которых может быть выполнена l-м числом вариантов (l = I, 2, ... , L) по применяемым материалам, технологии, оборудованию, средствам оснастки.

На основе изложенных принципов изготовления одежды стабильного ассортимента представляется возможным развернуть генеральную цель в иерархической графе целей и задач, которой применительно к минимизации критерия затрат представлен на рисуне.

В качестве критерия может быть выбрана также трудоемкость, расход ткани или какой-либо другой показатель.

В представленном на рисунке пятиуровневом графе целей и задач цели любого нижнего уровня могут рассматриваться как задачи, решение которых приводит к достижению целей верхнего уровня.

Процедура выбора оптимальных решений используется для достижения цели каждого уровня вплоть до уровня 0, т. е. – генеральной цели.

Таким образом, существо принятия решений при развертывании генеральной цели в иерархический граф целей и задач составляет выбор групп оптимальных целей из множества их совместных вариантов. С учетом ситуаций, встречающихся в практике изготовления изделия, возможны различные подходы к проблеме выбора оптимальных решений, отвечающих стратегии W→min (генеральной цели) или целей любого другого уровня, с которых начинается реализация задач по достижению генеральной цели.

Проблема выбора решений, отвечающих стратегии:

w =     в ij → min        (3)

Актуальна для отрасли и складывается из последовательности оптимальных решений, оптимальных для каждого потока (предприятия) отдельности.

В выражения (3)

Сij – затраты на изготовления i-го вида изделия на j-ом потоке;

вij – объем производства i -го вида изделия на j-ом потоке.

С учетом того, что значение вij для конкретного предприятия является величиной фиксированной, рассмотрена на основе связей, существующих между целями уровней 2, 3, 4, 5 графа (рис.), задача минимизации затрат (себестоимости) Сij , являющаяся одной из наиболее актуальных, при нормируемой трудозатрате – Т ij.

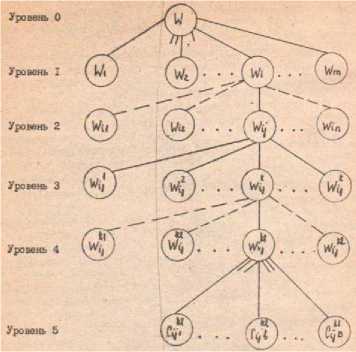
Рисунок 1. Граф целей и задач минимизации критерия затрат

В работе выделены типовые ситуации, возникающие в условиях массового производства одежды стабильного ассортимен- та, для которых решены задачи оптимального синтеза технологических процессов по критерию Cij:

– для одного изделия на одном потоке;

– для нескольких изделий (комплектов) на одном и нескольких потоках;

– для всей совокупности заданных видов изделий в рамках отрасли.

Приведем постановку задачи синтеза технологического процесса (m) для одного изделия при заданном суммарном времени изготовления Tij*.

Пусть ТП для i-го изделия включает K операций, каждая из которых может быть реализована различными вариантами. Обозначим множество вариантов для R –й операции через {L}k. Каждый вариант характеризуется значениями длительности выполнения t ij^ke стоимостью C ij^ke . Требуется определить последовательность вариантов реализации каждой операции так, чтобы выполнялись условия:

с = У Г" ^ min ij                       ij к=1

и

k

X j Т , к = 1

Процесс синтеза искомой последовательности вариантов представлен как многоэтажный, где этапу соответствует очередная операция, и для решения применен метод динамического программирования. Рекуррентное соотношение имеет вид:

kk

Х* • ГП* • fij I Tij 1 = ^min1

k к к 1 Т’* *  Т1* *

Cij +. fij I Tij - Ti^j

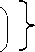
kk где fj [ Tij ]

минимальная стоимость

выполнения первых K операций;

k

Tij – длительность выполнения первых

K операций, определяющих «состояние» в схеме динамического программирования.

Аналогичным образом решается задача, когда требуется минимизировать затраты времени, расход ткани или какой-нибудь другой показатель фиксированной последовательности изготовления изделия. Для случая, когда допускается варьирование последовательности обработки деталей, оптимизационная задача сводится к задаче целочисленного программирования.

Приведённая методика определения затрат в работе использована и для случаев, когда один и тот же вид изделия может быть изготовлен выполнением разного по количеству числа операций. В этом случае решается Z оптимизационных задач отмеченного типа, в результате чего получают ряд величин , , , . Наилучшим является технологический процесс, отвечающий стратегии:

→min

Рассмотренные примеры оптимизационных моделей позволяют решить задачу синтеза технологии для изготовления одного изделия в рамках одного потока. Вместе с тем для некоторых предприятий и производственных объединений требуется решить задачу по оптимальному изготовлению нескольких видов одежды (комплектов) на имеющихся потоках в требуемых объемах.

Задача построения оптимального технологического процесса для комплекта изделий может быть сведена к решению нескольких (по числу изделий в комплекте) задач, постановка которых соответствует модели (4) с возможно дополнительным ограничением на общее время изготовления комплекта.

Отраслевая задача включает требование обеспечить выполнение задания по объему производства изделий с учетом мощностей потоков. В работе для этой задачи также предложена математическая модель и алгоритм решения по методу динамического программирования.

Аналогичным образом формируется в работе задача оптимизации производства применительно к другим критериям (трудозатратам – фонду рабочего времени, расходу ткани и т.д.).

Наряду с оценкой вариантов производства изделия на основе одного критерия ( стоимости, трудозатрат или расхода ткани ) в работе предложена многокритериальных задач осуществляют с помощью привлечения дополнительных гипотез [3].

Допустим, требуется решить оптимизационную задачу, отвечающую стратегиям:

Cij→ min; Tij→ min; Sij→ min (6) где,

Tij – затрата времени на изготовление i-го изделия на j-ом потоке;

Sij – масса i-го изделия, изготавливаемого на j-ом потоке;

Tij≤ Tij* и Sij≤ Sij*       (7)

мы получаем возможность свести многокритериальную задачу к однокритериальной:

Cij→min         (7)

при ограничениях (7)

Аналогичным образом может решаться задача минимизации

W→min, A→min где A – фонд рабочего времени, необходимый для изготовления i-х заданных видов изделия на j-х потоках в требуемых объемах.

Выбор оптимального варианта производства высококачественной одежды стабильного ассортимента осуществляется из множества допустимых вариантов на основе математического описания технико- экономических критериев и ограничивающих условий (математических моделей), учитывающих совокупность свойств элементов одежды (узлов и деталей), а также технологий, используемых для их обработки (в том числе свойств трудовых ресурсов, оборудования, транспортных средств, организационной и технологической оснастки). Для определения допустимости генерируемых вариантов изготовления одежды по функциональным свойствам предложены и осуществлены инструментальные и экспертные методы оценки качества.