Совершенствование предметной компетентности учителя математики в решении профессиональных задач

Введение. Учитель математики в школе для обучающегося является источником нового предметного знания, проводником современных идей, методов, технологий, обеспечивающих формирование и развитие у учеников компетенций, ориентирующих их на более эффективные способы деятельности при решении различного класса задач. Кроме того, наблюдается рост «общественного запроса на качественное математическое образование и повышение роли математической грамотности как общественно-значимого фактора» [1, с. 245].

Для подготовки и обучения профессионалов в системе образования всегда, «в первую очередь требуется развитие их профессиональных компетентностей» [2, с. 85].

В связи с этим, уровень профессионализма учителя и будущая успешность в профессии определяются качеством его фундаментальной математической подготовки, уровнем сформи-рованности теоретических знаний по предмету, умений и навыков оперирования с математическими объектами и др., то есть предметной компетентностью.

Предметная компетентность особенно необходима учителям для качественной подготовки обучающихся к сдаче единого государственного экзамена по математике и участия в предметной комиссии ГИА.

Результаты диагностики предметной компетентности учителей Ямало-Ненецкого автономного округа показали, что у учителей математики возникают трудности применения математических знаний при решении математических задач повышенной сложности.

В соответствии с данной проблемой цель нашего исследования заключается в определении и обосновании педагогических условий совершенствования предметной компетентности учителя математики в условиях цифровизации образования.

Поскольку предметная компетентность учителя должна постоянно совершенствоваться, то для достижения этой цели наилучшим образом подходит система дополнительного образования педагогов. В системе повышения квалификации учителей создаются наиболее благоприятные условия для корректировки и систематизации предметных знаний учителя, компенсации его знаниевых дефицитов, связанных с недостатком когнитивных ресурсов. В этой связи для решения фундаментальной задачи повышения предметной компетентности учителей в системе дополнительного образования, отвечающей всем глобальным вызовам в сфере образования на современном этапе ее развития, с 2020 года на базе Ярославского государственного педагогического университета им. К. Д. Ушинского функционирует научнометодический центр сопровождения педагогов — центр трансфера образовательных технологий «Новая дидактика». В рамках деятельности данного центра разрабатываются и реализуются не только различные программы повышения квалификации учителей, но и новые дидактические решения, нацеленные на преодоление у действующих педагогов множества профессиональных дефицитов.

Обзор литературы. Вопросам формирования предметной компетентности будущего учителя математики еще при обучении в педагогическом вузе посвящены, например, работы Н. Л. Стефановой, Т. С. Волковой [3], Л. В. Шке-риной [4] и др. исследователей.

Однако предметная подготовка будущих учителей математики в вузе не всегда в полной мере обеспечивает их качественную подготовку. Для устранения дефицитов в предметной подготовке учителей математики предлагается использовать ресурсы дополнительного профессионального образования.

Аспекты повышения профессионализма учителей математики в системе повышения квалификации рассмотрены в работах различных исследователей.

Так, А. В. Камышов предлагает к реализации в рамках системы дополнительного образования учителей математики программу повышения квалификации, посвященную решению задач с параметрами в средней школе [5].

В своей работе [6] авторы обосновывают необходимость разработки модульных программ повышения квалификации педагогов с целью обеспечения персонифицированной им помощи в устранении профессиональных затруднений.

Выявлению существенных факторов связи профессиональных дефицитов учителей с образовательными результатами школьников посвящена работа Л. А. Новопашиной, Е. Г. Григорьевой, Д. В. Кузиной, Ю. А. Черкасовой. Авторы отмечают, что учебная результативность школьников напрямую «зависит от специфики профессиональных дефицитов, умений и компетентностей учителей» [7, с. 21].

На основе проведенного сопоставительного анализа результатов ЕГЭ по математике профильного уровня выпускников 11-х классов с результатами тестирования учителей математики, показавшего прямую корреляционную зависимость между решаемостью заданий учителями и учащимися, В. Р. Попова [8] предлагает организовать работу проектных и методических мастерских. В рамках работы проектной мастерской проектируется тематическая линия базовых задач, а в рамках методической мастерской — разложение сложной задачи на базовые с учетом возрастных способностей обучающихся.

Д. Ю. Амерева [9] утверждает, что при реализации персонализированной дополнительной профессиональной программы может быть использована стажировка учителя, в том числе виртуальная.

В работе В. П. Вейдт [10] представлены предложения по совершенствованию модели повышения квалификации педагогов через изменение содержания дополнительных профессиональных программ, процедуры выстраивания индивидуального образовательного маршрута с учетом профессионального стандарта педагога. Автор предлагает перед построением индивидуального образовательного маршрута педагога проводить входное тестирование педагога на уровень владения предметной областью.

Построение индивидуальной траектории обучения слушателей на основе сочетания различных игровых, активных и интерактивных методов обучения, в частности веб-квеста, предложено в работе [11], показана необходимость интеллектуальной и профессиональной самообразовательной работы учителя математики в межкурсовой период — гибкой и мобильной системы, которая решает задачи учебно-методического обеспечения на основе удо- влетворения потребностей педагогов в профессиональном совершенствовании с использованием дистанционных и онлайн-технологий.

Мы разделяем позицию, сформулированную в статье [12], посвященной вопросам совершенствования системы непрерывного педагогического образования в условиях цифровизации образования, согласно которой должна быть обеспечена «приоритетность неформального образования в повышении профессионального мастерства педагогических работников: мастер-классов, семинаров, стажировочных площадок и др. аналогичных мероприятий». В этом случае учитель будет выступать активным субъектом в построении личной траектории профессионального роста.

На основании вышеизложенного можно сделать вывод об актуальности и значимости обучения учителей математики в центрах дополнительного профессионального образования. Следовательно, вполне логично определить и обосновать педагогические условия совершенствования предметной компетентности учителя математики в системе дополнительного профессионального образования с учетом использования различных форм и технологий обучения, в том числе, и сетевых технологий.

Методология (материалы и методы).

Методологической основой исследования выступают положения компетентностного подхода в образовании, согласно которым возникает потребность формирования у учителей необходимых компетенций и, как следствие, создание специальной системы подготовки и переподготовки педагогических кадров.

Состояние сложного образовательного пространства профессионально-педагогической подготовки учителя можно охарактеризовать терминами синергетики: аттрактор, бифуркация, флуктуация, которые соотносятся с базовыми понятиями традиционной педагогики, раскрывая их роль в развитии предметной компетентности учителя математики. Осмысление и переосмысление содержания предметного знания, соотнесение его сущности с актуальными значениями, установление причинноследственных и интуитивных связей учителям математики в рамках системы дополнительного образования позволяет использовать синергетический подход для совершенствования предметной компетентности педагога. Во время этого процесса появляются на основе дивер- гентности и открытости коммуникаций новые цели, методы и средства подготовки, меняется содержание образовательных конструктов, возникает нелинейность как образовательного процесса, так и педагогического результата. Увеличивающаяся насыщенность образовательного информационного пространства и его синергия выводят систему коммуникаций из устойчивого равновесия, возникают ситуации неопределенности, проблемные ситуации. При этом ситуативные проявления аттрактора наблюдаются в виде наличия относительно устойчивых возможных состояний взаимодействия при актуализации процессов проявления единства во множественных суждениях о сущности математических проблем, тогда как бифуркация присутствует в критический момент неопределенности будущего развития личности преподавателя, когда появляются альтернативные развилки веера возможностей.

Результаты и их описание

В Ямало-Ненецком автономном округе был проведен мониторинг предметных компетенций учителей математики общеобразовательных организаций, направленный на решение следующих задач:

• 1.    Выявление учителей математики, обладающих высоким уровнем сформированности предметных компетенций и способных качественно подготовить обучающихся к сдаче ЕГЭ по математике и участия в предметной комиссии ГИА.

• 2.    Определение предметных затруднений учителей математики.

• 3.    Совершенствование у учителей предметных компетенций, необходимых для обеспечения высокого качества образования.

• 4.    Создание благоприятных условий для профессионального роста педагогов посредством разработки индивидуальных образовательных маршрутов педагогических работников.

Всего в диагностике приняло участие 261 учитель математики.

Диагностика включала в себя следующие 13 базовых разделов школьного курса математики, которые позволяют определить уровень сформированности предметных компетенций учителей математики:

• 1.    Действительные числа.

• 2.    Уравнения.

• 3.    Неравенства с параметром.

• 4.    Неравенства.

• 5.    Финансовая математика.

• 6.    Начала математического анализа.

• 7.    Координаты и векторы.

• 8.    Планиметрия.

• 9.    Планиметрия (высокий уровень).

• 10.    Стереометрия.

• 11.    Тригонометрия.

• 12.    Элементы комбинаторики и теории вероятностей.

• 13.    Числовые задачи (последовательности).

В тестировании использовались следующие формы ответов: выбор одного варианта ответа, ввод численного ответа, установление соответствия и упорядочивание.

В соответствии с количеством набранных баллов были определены следующие уровни сформированности предметных компетенций учителя: недопустимый; базовый; повышенный и высокий. Результаты диагностики учителей представлены в таблице 1.

Таблица 1

Результаты диагностики предметных компетентности учителей общеобразовательных организаций Ямало-Ненецкого автономного округа

Компетенции	Справились с заданием, %	Частично справились, %	Не справились, %
Действительные числа (повышенный уровень)	91	5	4
Уравнения (базовый уровень)	70	0	30
Неравенства с параметром (повышенный уровень)	66	0	34
Неравенства (повышенный уровень)	55	25	20
Финансовая математика (базовый)	79	16	5
Начала математического анализа (повышенный уровень)	56	3	41
Координаты и векторы (повышенный уровень)	56	30	14

Компетенции	Справились с заданием, %	Частично справились, %	Не справились, %
Планиметрия (базовый уровень)	89	0	11
Планиметрия (высокий уровень)	43	0	57
Стереометрия (высокий уровень)	29	42	29
Элементы комбинаторики и теории вероятностей (повышенный уровень)	84	0%	16
Тригонометрия (повышенный уровень)	74	0	26
Числовые задачи (последовательности) (повышенный уровень)	65	0	35

Результаты анкетирования показали, что у учителей достаточный уровень базовых знаний и умений, которые связаны в большей степени с базовыми знаниями содержания предмета, но в тоже время вызвали затруднения задачи по началам математического анализа и неравенства с параметрами, так как данные задачи были высокого уровня сложности.

Анализ работ учителей показал, что наибольшие затруднения вызвали следующие виды задач:

— Неравенства (повышенный уровень), в том числе неравенства с параметрами.

— Начала математического анализа (повышенный уровень).

— Координаты и векторы (повышенный уровень).

— Планиметрия (высокийуровень).

— Стереометрия (высокий уровень).

Приведем примеры перечисленных выше видов задач, включенных в КИМы, и некоторые методические комментарии к их решению.

Начала математического анализа

Задание на выбор одного варианта ответа

Каково наименьшее расстояние от точки А (2;   0) до точек графика функции

?

3    ^27 (х-2)

Определите, в каком из промежутков находится ответ на вопрос задачи и укажите его номер:

1) '.- \;             2) У- ' Л;;

• 3,  : :              40,25 ;0,3];    5) - |].

В конус, высота которого равна 1 и угол при вершине осевого сечения равен - вписываются всевозможные цилиндры. В каких пределах изменяется при этом объем цилиндра?

Выберите верный вариант ответа и укажите его номер:

1) с 5:

• 3) ^ ^;

• 5)    другой вариант.

  2> ' ^

  ⁴> С -Г"

  
  

Приведенные задачи могли вызвать затруднения у учителей в связи с тем, что по условию требуется составить функции для исследования и, при этом, использовать знания как из раздела алгебры и начал анализа, так и по геометрии.

При исследовании составленной функции, являющейся математической моделью ситуации, описанной в условии задачи, учителю стоило обратить внимание на то, что требование задачи может быть сформулировано по- разному:

— найдите наибольшее (наименьшее) значение функции;

— найдите область значений функции;

— определите, в каких пределах изменяется оптимизируемая величина.

Планиметрия

Задание на выбор одного варианта ответа

Найдите радиус окружности, проходящей через точку пересечения диагоналей равнобедренной трапеции и касающейся большего основания и боковых сторон трапеции с основаниями 1 и 8. Выберите верный вариант ответа и укажите его номер:

1) V;        ²> ¥

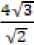
4) 5

5) другой вариант.

При решении задачи требуется выполнить дополнительное построение — провести прямую, параллельную основаниям и проходящую через точку пересечения диагоналей трапеции; после чего рассмотреть окружность, вписанную в равнобедренную трапецию. Далее использу- ется подобие треугольников; свойство касательных, проведенных к окружности или свойство четырехугольника, описанного около окружности. Возможно найти высоту трапеции (диаметр окружности), зная ее стороны; или найти радиус, проведенный к боковой стороне трапеции, как высоту прямоугольного треугольника. Требуемые для решения задачи знания разных разделов курса планиметрии не выходят за рамки базовых. Задачу необходимо разбить на типовые подзадачи, что, возможно, и вызвало затруднения при ее решении.

Таким образом, результаты анкетирования показали, что предметные знания учителей математики нуждаются в дальнейшей корректировке.

Как справедливо отмечает Л. В. Шкерина, одной из причин профессиональных дефицитов учителя математики является недостаточность распространения «адресного повышения квалификации учителя, направленного на устранения конкретных пробелов в знаниях педагога» [13, с. 87].

Полагаем, что наиболее благоприятные условия для корректировки и систематизации предметных знаний учителя математики, компенсации его профессиональных дефицитов создаются при реализации системы комплексного непрерывного повышения компетентности педагога, включающей курсы повышения квалификации, построение индивидуальных образовательных маршрутов педагогов, проведение стратегических сессий, практикумов, методических семинаров, обмен опытом педагогов и трансляцию эффективных практик по проблемным вопросам.

Таким образом, перед системой ДПО ставится актуальная задача адресной поддержки педагогов на протяжении всей педагогической деятельности. Доминирующим направлением в адресной поддержке педагогов с целью повышения их предметной компетентности являются программы повышения квалификации учителей, в том числе и в дистанционном формате.

На основе диагностики учителей математики и выявленных затруднений необходимо в программу курсов повышения квалификации педагогов включить следующие вопросы.

• 1.    Выполнение действий с геометрическими фигурами, решение задач на координатный метод.

• 2.    Решение неравенств с параметрами.

• 3.    Построение и исследование простейших математических моделей.

• 4.    Планиметрические понятия и методы при решении стереометрических задач.

• 5.    Метод координат при решении стереометрических задач в ЕГЭ по математике.

В рамках методических семинаров для учителей математики возможно организовать обсуждение методических подходов к работе с одаренными детьми, аспекты подготовки обучающихся к ГИА в 9-х и 11-х классах, выполнение различных кейс-заданий. Приведем пример кейс-задания и результат его обсуждения учителями.

Кейс-задание. На уроке обобщения и систематизации знаний по теме «Уравнения и неравенства, содержащие переменную под знаком модуля. Урок одной задачи» в 10-м классе предложено решить неравенство разными способами. В результате «мозгового штурма» были выявлены некоторые способы решения данной задачи. Класс разделился на группы, каждая из которых выбирает определенный способ решения и выполняет его.

Задания:

• —    решите данное неравенство одним из найденных учащимися способов;

• —    перечислите положительные стороны применения групповой работы на уроке одной задачи;

• —    опишите, как организовать работу групп и всего класса в целом;

• — укажите, как происходит учет индивидуального вклада каждого;

— опишите, как можно организовать подведение итогов работы групп.

Вам необходимо ознакомиться с представленными способами решения неравенства и написать комментарии по каждой из указанных выше позиций.

Решите неравенство:

4 x - 2

≥ x - 2 x + 1

1-й способ. Метод интервалов или раскрытие знака модуля по определению.

2-й способ. Учитывая то, что неравенство может иметь решение только при условии 4x - 2 ≥ 0 , то есть при x ≥ , замена исходного x- неравенства равносильным:        ≥ x - 2

x + 1

(почему?) и решение методом интервалов или раскрытием знака модуля по определению.

3-й     способ.     Замена     неравенства x-2 ≤

4 x - 2

равносильной ему системой.

x + 1

4-й способ. Возведение обеих частей неравенства в квадрат.

5-й способ. Графический (2 способа).

Результат обсуждения учителей может быть представлен в формах ответов (табл. 2).

К особенностям формирования предметных компетенций у учителей математики в системе ДПО с использованием различных форм и технологий обучения отнесем проведение стратегических сессий, построение индивидуальных образовательных маршрутов педагогов, реализацию персонифицированного учета и консультирование учителей по различным вопросам на основе использования информационнообразовательной среды (ИОС).

Результаты

Таблица 2

Выполнение задания	Комментарии
Приведено правильное решение неравенства одним из способов	Способ решения — на выбор экзаменуемого. Ответ: [1; 5]
Перечислены положительные стороны применения групповой работы на уроке одной задачи	— создание благоприятных условий для обобщения и систематизации в условиях совместного обсуждения; — возможность самостоятельно найти разные способы решения задачи в результате групповой работы; — создание ситуации успеха для каждого участника группы; — совместная работа способствует выявлению собственных ошибок и их причин; — групповая работа повышает познавательную активность каждого и способствует формированию учебной мотивации; — урок одной задачи с использованием групповой работы содействует развитию математического мышления школьников и исследовательских учебных умений
Описано, как организовать работу групп и всего класса в целом	1.    В группах учащиеся могут распределить роли: — ведущий, который в завершении будет представлять результат работы группы; — консультант, который помогает понять и уточнить все шаги решения и отвечает на вопросы при защите; — технические секретари, оформляющие решение. 2.    Участники группы обсуждают план решения, выполняют его самостоятельно и совместно анализируют полученные результаты, формулируют выводы о результатах проделанной работы. 3.    Учитель в начале напоминает о правилах поведения в группах, формах подведения итогов работы групп и класса в целом. 4.    Учитель консультирует группы в случае необходимости, способствует созданию комфортной работы на уроке, следит за временем
Указано, как происходит учет индивидуального вклада каждого	Учет, с одной стороны, ведет учитель из наблюдений за работой групп. С другой стороны, по завершении работы группы производится оценка участниками группы ее работы и самооценка каждого. При этом оценивается не личность участника группы, а его деятельность при работе в группе
Описано, как можно организовать подведение итогов работы групп	Каждая группа представляет у доски свой способ решения задачи, остальные обсуждают предложенный способ и фиксируют его. Ведущий рассказывает решение, консультант отвечает на вопросы. Общий итог работы учащиеся подводят самостоятельно после выступления всех групп, обобщая полученные выводы по результативности проведенной работы

Под ИОС будем понимать систему инструментов, ресурсов и средств, способствующих эффективному совместному информационному взаимодействию всех субъектов образовательного процесса, познавательной деятельности на основе использования различных распределенных информационных ресурсов.

Для организации ИОС в рамках системы ДПО наилучшим образом подходит платформа Moodle, реализующая философию «педагогики социального конструкционизма» и предоставляющая «существенное расширение возможностей традиционных форм обучения» [14, с. 22], интерактивного доступа ко всем образовательным ресурсам в любом месте и в любое время.

С использованием платформы Moodle в личном кабинете педагога возможен различный набор элементов индивидуальной траектории обучения с учетом степени подготовленности учителя, скорости усвоения материала и др.: теоретический материал, задания, глоссарий, форум, тест и др.

Формой интеграции фундаментальной и профессионально-педагогической составляющих в развитии предметной компетентности учителя математики являются сетевые сообщества педагогов, участники которых объединены по интересам и их взаимодействие способствует актуализации личностного опыта, профессиональному развитию учителя. В сетевом сообществе возможно организовать стратегические сессии по обсуждению методических подходов к работе с одаренными детьми, обсудить аспекты подготовки обучающихся к ГИА в 9-х и 11-х классах и др. вопросы, связанные с освоением сложного математического знания.

Совершенствование предметной компетентности учителя математики в сетевом сообществе должно происходит за счет осуществления методической деятельности педагогов при решении учебных и учебно-методических разноуровневых задач; поэтапного «фундирования опыта личности и актуализации индивидуального стиля деятельности педагога» [15, с. 7]. Принцип фундирования процесса повышения квалификации учителя, по мнению Д. И. Прохорова, «определяет основные направления становления личности учителя математики в опоре на спиралевидное обогащение, расширение и углубление предметно-методических профессиональных компетенций» [16, с. 220].

На основе проведенного теоретического исследования, анализа диагностики сформиро-ванности предметной компетентности у учителей математики определим и обоснуем педагогические условия совершенствования предметной компетентности учителя математики с использованием ресурсов системы ДПО.

• 1.    Педагогическое условие — актуализация группы мотивационных установок на совершенствование профессионального мастерства учителя и формирование мотивационноценностного компонента предметной компетентности учителя математики. Педагоги должны быть заинтересованы в осуществлении учебной деятельности, в повышении своего профессионализма. С этой целью в содержание курсов ДПО должны быть включены разнообразные педагогические кейсы, в которых описаны реальные учебные ситуации из профессиональной деятельности современного учителя математики.

• 2.    Обеспечение непрерывного и целостного развития предметной компетентности учителя математики в течение всей его профессиональной деятельности на основе обучения в ИОС.

• 3.    Обеспечение единства предметной, операциональной и профессионально-педагогических характеристик содержания и технологий изучения методов решения математических задач на основе коммуникативной деятельности учителей в сетевом сообществе. Реализация этого условия позволяет развить у педагога представления о возможных способах поведения, ценностях профессиональной деятельности и собственной роли в ней и рассмотреть процесс обучения математике как формирование опыта продуктивной учебной деятельности учителя через накопление индивидуального, личного педагогического опыта.

Обсуждение

Основная часть исследования состояла в анализе профессиональных дефицитов учителей математики и определении возможных путей их устранения в рамках дополнительного профессионального обучения педагогов. В процессе исследования были определены и обоснованы педагогические условия совершенствования предметной компетентности учителя математики в овладении способами решения математических задач повышенной сложности с использованием ресурсов системы

ДПО. Перспективным направлением дальнейшей исследовательской работы нам представляется в разработке программ повышения квалификации учителей математики на основе сетевых технологий, а также разработке системы онтологий для обеспечения взаимосвязей и согласованности различных исследований, то есть выполнение онтологического инжиниринга содержания предметной компетентности учителя математики, что будет способствовать структуризации основных понятий и разработке методологических основ этого процесса. Рассмотренные в статье актуальные вопросы требуют широкого обсуждения не только в научном сообществе преподавателей системы ДПО, но и в педагогической среде учителей математики.

Заключение

На основе проведенного исследования заключаем, что рост общественного запроса на качественное математическое образование и повышение роли математической грамотности как общественно значимого фактора в настоящее время позволяет актуализировать одну из самых важных проблем в современном образовании — повышение предметной компетенции учителя математики.

Результаты предметной диагностики учителей показали, что большинство из них не справляются с заданиями по математике высокого уровня сложности.

Для корректировки и систематизации предметных знаний учителя, компенсации его знаниевых дефицитов, связанных с недостатком когнитивных ресурсов, наиболее благоприятные условия создаются в системе дополнительного профессионального образования на основе синергетического подхода через осмысление и переосмысление содержания предметного знания, соотнесение его сущности с актуальными значениями, установление причинноследственных и интуитивных связей при решении математических задач.

К особенностям формирования предметных компетенций у учителей математики в системе ДПО отнесены следующие: проведение стратегических сессий, построение индивидуальных образовательных маршрутов педагогов, реализация персонифицированного учета и консультирование учителей по различным вопросам на основе использования информационно- образовательной среды, например платформы Moodle, а также взаимодействия педагогов в сетевом сообществе.

На основе проведенного исследования заключаем, что для устранения профессиональных дефицитов и совершенствования предметной компетентности учителей математики целесообразна реализация следующих условий:

• —    разработки модульных программ повышения квалификации учителей с обеспечением их методическими материалами;

• —    актуализации группы мотивационных установок на совершенствование профессионального мастерства учителя на основе включения в содержание курсов ДПО разнообразных педагогических кейсов, в которых описаны реальные учебные ситуации современного учителя математики;

• —    активного использования ИОС, в том числе сетевых сообществ педагогов;

• —    адресной поддержки педагогов на протяжении всей педагогической деятельности.

В качестве перспектив мы рассматриваем обогащение методического инструментария проведением онтологического инжиниринга содержания предметной компетентности учителя математики, что будет способствовать структуризации основных понятий и разработке методологических основ этого процесса.