Совершенствование программы технического обслуживания пассажирских лифтов на основе имитационного моделирования режимов их работы

Введение. Согласно основному нормативному документу1, лифт — это устройство, предназначенное для перемещения людей и (или) грузов с одного уровня на другой в кабине, движущейся по жестким направляющим, у которых угол наклона к вертикали составляет не более 15°. Лифт является уникальным транспортным средством массового пользования. Им управляет сам пассажир или персонал, которому не требуется высокой квалификации [1] Поэтому лифт должен отвечать всем требованиям безопасности и комфортности при перевозке пассажиров. Лифт относится к числу сложных электромеханических устройств повышенной опасности [2]. К проектированию, изготовлению, монтажу и техническому обслуживанию лифтов в процессе эксплуатации предъявляются жесткие требования, сформулированные в Техническом регламенте и других нормативных документах. В зависимости от типа привода лифты бывают электромеханические и гидравлические [3]. В электромеханических лифтах в качестве подъемного механизма применяется привод, состоящий из электродвигателя, редуктора и канатоведущего шкива (рис. 1), а в гидравлических — гидропривод поступательного действия.

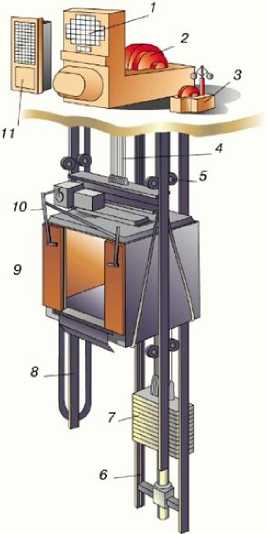
Рис. 1. Конструкция лифта с электромеханическим приводом: 1 — электродвигатель;

• 2    — лебедка; 3 — ограничитель скорости; 4 — тяговые канаты; 5 — направляющие ролики кабины;

• 6    — направляющие противовеса; 7 — противовес; 8 — направляющие кабины; 9 — кабина;

• 10    — дверной механизм; 11 — пульт управления

Наибольшее распространение в современных многоэтажных зданиях получили лифты с электромеханическим приводом [4]. В настоящей статье предметом исследования являются лифты с редукторным электромеханическим приводом.

В конце 2020 года, согласно информации Национального лифтового союза, в Российской Федерации насчитывалось более 500 тыс. лифтов, эксплуатируемых в жилом фонде и различных учреждениях 2 . Порядка 160 тыс. из них отработали свой установленный нормативный срок, но продолжают эксплуатироваться. С каждым годом увеличивается количество новых многоэтажных строений по всей стране, что приводит к росту фонда лифтового оборудования.

Наиболее важными требованиями, предъявляемыми к лифтовому оборудованию, являются безопасность и комфортность пассажиров, которые могут быть обеспечены за счет правильного выбора параметров вертикальной транспортной установки и постоянного поддержания лифта в исправном состоянии [4–5].

На показатель безопасности лифта основное влияние оказывают следующие группы факторов:

• —    качество изготовления лифтового оборудования;

• —    уровень загруженности несущих элементов и его соответствие нормативным значениям с учетом величины отработанного ресурса;

• —    реализуемая программа технического обслуживания.

  Машиностроение и машиноведение

  
  

  • ² Данные Национального лифтового союза РФ / URL: http://www.lift.ru/index.php/ru/ebiblio.html (дата обращения: 11.05.2021).

Безопасность лифта 3 характеризуется общепринятыми показателями: наработка на отказ, вероятность безотказной работы, коэффициент готовности.

Показатель «транспортная комфортность» введен национальным стандартом 4 . Он характеризует интервал движения лифтов, выраженный в виде периода времени между двумя последовательными отправлениями кабины лифта в заданном направлении на основном посадочном этаже, на котором входящие в здание люди имеют доступ к лифтам. Таким образом, уровень комфортности — это условное время ожидания пассажиром очередного рейса. Отметим, что показатель транспортной комфортности является случайной величиной и, естественно, в реальных условиях изменяется от минимального до максимального значения. Наиболее представительной величиной показателя комфортности может являться средняя величина в различные периоды суточной эксплуатации.

Обратимся к программам технического обслуживания лифтов. Периодичность ТО лифтового оборудования устанавливается исходя из двух основных документов: паспорта оборудования и «Правил…» 5 . Периодичность принята одинаковой для всех объектов лифтового хозяйства.

В последние годы выполнен ряд фундаментальных исследований в России [4–6] 678 и за рубежом [7–10], относящихся к обеспечению надежности и безопасности лифтового оборудования. Следует отметить, что в рассмотренных работах при установлении периодичности ТО лифтов не принимаются во внимание такие параметры, как плотность заселения этажей и квартир, а также уровень силовых нагрузок, реальное время работы лифта, количество включений главного привода в единицу времени.

Несмотря на одинаковую этажность, идентичный тип и количество лифтов аналогичные строения могут значительно отличаться по количеству проживающих, а также по степени эксплуатации лифтового оборудования. Это оказывает существенное влияние на чистое время работы, эквивалентные нагрузки, испытываемые лифтовым оборудованием, что изменяет реальный темп отработки ресурса, срок службы каждого комплекта лифтового оборудования. При этом плановый назначенный срок службы их будет одинаков.

Важно отметить, что в нормативных 3,4,5 и литературных отечественных [6] 6,7,8 и зарубежных [7–10] источниках к настоящему времени отсутствуют определение и рекомендации по применению критериев загруженности лифтов. Нет также аналитических и инженерных методов проектирования программ ТО лифтов в разработках научно-исследовательских, проектных и эксплуатационных организаций. Отсутствие методической базы по проектированию системы и программы ТО лифтов приводит в одних случаях к превышению необходимого объема ремонтных воздействий с одновременным ростом затрат, в других — к необоснованному увеличению межремонтного интервала. Это сказывается на снижении показателей надежности и в целом на безопасности при эксплуатации лифтовых установок.

Для поддержания уровня безопасности и комфортности лифтовых установок при необходимом и достаточном уровне ремонтных воздействий в настоящей работе предусматриваются исследования в следующих направлениях:

• —    использование имитационного моделирования для установления реальных эквивалентных нагрузок и режимов работы;

• —    обоснование комплексного показателя, с помощью которого можно сформировать оценку уровня нагруженности силовых элементов лифта;

• —    разработка рекомендаций по периодичности обслуживания лифтов как в уже эксплуатируемых, так и в проектируемых зданиях.

Это позволит контролировать правильность принятых проектных решений (прежде всего по параметрам главного привода), за счет эффективной организации ТО снизить вероятность возникновения отказов в работе оборудования.

Следует отметить, что при моделировании лифтовых установок, находящихся в эксплуатации, можно использовать кинематические показатели режима, полученные в результате наблюдений диспетчерских служб: 3

Национальный стандарт Российской Федерации. Лифты. Общие требования безопасности при эксплуатации : ГОСТ Р 55964-2014 / Федеральное агентство по техническому регулированию и метрологии. Москва : Стандартинформ, 2019. 16 с.

• 4    Национальный стандарт Российской Федерации. Лифты пассажирские. Проектирование систем вертикального транспорта в жилых зданиях : ГОСТ Р 52941-2008 / Федеральное агентство по техническому регулированию и метрологии. Москва : Стандартинформ, 2008. 15 с.

• 5    Правила организации безопасного использования и содержания лифтов, подъемных платформ для инвалидов, пассажирских конвейеров (движущихся пешеходных дорожек) и эскалаторов, за исключением эскалаторов в метрополитенах / Утверждены постановлением Правительства РФ от 24 июня 2017 года № 743. URL: https://docs.cntd.ru/document/436745439#/reg/ (дата обращения: 11.06.2021).

• 6    Мечиев, А. В. Разработка путей обеспечения безопасной эксплуатации лифтов : автореф. дис. … канд. техн. наук / А. В. Мечиев. Москва, 2018. 18 с.

• 7    Горожеев, М. Ю. Разработка и исследование прибора для экспресс-диагностики лифтов в процессе их эксплуатации : автореф. дис. … канд. техн. наук / М. Ю. Горжеев. Москва, 2013. 25 с.

• 8    Федяев, Р. В. Методы повышения надежности лифтов и подъемников : автореф. дис. … канд. техн. наук / Р. В. Федяев. Томск, 2013. 23 с.

чистое машинное время и удельное количество включений [11]. Для этих лифтов актуальным является получение в результате моделирования данных по силовым нагрузкам.

При комплексном моделировании режимов работы проектируемых лифтов необходимо предварительно решить задачу выбора их основных параметров.

Целью работы является научное обоснование концепции и методики разработки программы технического обслуживания конкретных лифтовых установок на базе исследований уровня и режима нагружения основных несущих узлов в течение заданного или прогнозируемого периода эксплуатации.

Материалы и методы. Континуальная постановка задач. В соответствии с общей концепцией решения проблемы и для достижения цели настоящей работы определены структура задач и методическое обеспечение каждого направления. Прежде всего планируется выполнить описание объекта моделирования как системы массового обслуживания, работающей в циклическом режиме и подвергающейся случайным внешним воздействиям. Предварительно необходимо изучить совокупность случайных факторов, воздействующих на главный привод лифтовой установки.

Эффективным методическим приемом исследования закономерностей рабочих процессов в условиях случайных воздействий признано имитационное моделирование. Для реализации процедур моделирования необходимо обосновать математические модели формирования силовых воздействий на привод лифтовой установки и модели формирования распределений случайных воздействий. К основным влияющим случайным факторам отнесены число пассажиров в кабине случайного рейса, номера этажей стояния, вызова и назначения, количество остановок в период цикла, продолжительность чистого машинного времени и общей продолжительности цикла.

Предусматривается разработка алгоритмов и программ имитационного моделирования влияния важнейших факторов на величину эквивалентных нагрузок и кинематические характеристики режима работы привода лифтовой установки на основе одного из современных языков программирования.

Необходима оценка адекватности и анализ результатов имитационного и силового моделирования для построения обобщенных зависимостей влияния основных факторов на режимные показатели лифтовых установок.

Впервые предусматривается формирование концептуальных подходов к разработке программ технического обслуживания лифтового оборудования во взаимосвязи с реальными режимами его нагружения и последующей разработкой инженерной методики формирования регламента ТО лифтовой установки.

В статье даются результаты представления лифта как системы массового обслуживания, выбора показателя эквивалентной нагрузки, модели формирования силовых воздействий на вал главного привода. Другие этапы и результаты моделирования кинематических показателей и силовых режимов будут представлены в очередных номерах журнала.

Результаты исследования. Лифт как система массового обслуживания. Для адекватного математического описания функционирования пассажирского лифта в многоэтажном доме необходимо принять некоторые очевидные условия, определяющие его основные свойства. Каждая лифтовая установка характеризуется паспортными параметрами, определяющими условия работы и ее возможности:

Машиностроение и машиноведение

• —    этажность дома, N;

• —    максимальная грузоподъемность, выраженная массой поднимаемого груза Q, кг, или количеством пассажиров, R;

• —    установившаяся скорость движения кабины (и противовеса), v, м/с.

Прежде всего необходимо принять, что работа лифтовой установки при перемещении пассажиров производится отдельными циклами. Каждый i-й цикл состоит из отдельных этапов: появление пользователей, случайное их число r, на случайном этаже M и вызов кабины; кабина лифта по окончании предыдущего цикла находится на случайном этаже L; кабина перемещается при Q=0 в период вызова с этажа L на этаж M; посадка r пассажиров на этаже M и движение на случайный этаж назначения S, 1≤r≤R; в процессе движения на участке M→S возможны случайные по числу Υ и расположению в здании промежуточные остановки для посадки и высадки отдельных пассажиров; высадка пассажиров на этаже назначения S; по окончании перемещения кабины в i-м цикле возникает пауза случайной продолжительностью Δi — ожидание очередного цикла.

Из описания следует, что лифт может быть представлен как оригинальная одно- или многоканальная система массового обслуживания — СМО [12], работающая в режиме воздействия ряда случайных факторов — M, L, S, r, Υ, Δ. Отличительная особенность лифтовой СМО в том, что продолжительность обслуживания заявки от момента вызова до доставки пассажира на конечный этаж назначения S является функцией многих случайных переменных. Каждые из случайных величин (M, L, S, r) являются независимыми. Функции распределения этих величин могут быть установлены либо опытным путем, либо на основе логического анализа. Отдельная задача решена для установления случайной величины — числа промежуточных остановок Υ [13,14]. Известное классическое решение может быть использовано только для описания случайного времени ожидания очередного цикла Δ.

В теории СМО доказано, что, если

• а)    вероятность поступления очередной заявки p n (t) зависит только от промежутка времени между

заявками t,

• б)    два события никогда не происходят в один и тот же момент времени,

• в)    вероятность того, что за очень малый промежуток времени Δt, выбранный в любой момент,

произойдет хотя бы одно событие, то вероятность p n (t) выражается законом Пуассона [12]:

PnW =

(Xt)ne-xt

.

n!

Распределение интервала времени между двумя последовательными случайными событиями Τ подчиняется экспоненциальному закону, т. е.

P(T>t)=e-T, где среднее значение случайной величины Т равно

τср=1/λ.

Таким образом, для моделирования потока заявок, поступающих на вход одиночного лифта, можно принять экспоненциальный закон распределения интервала Δ. При этом необходимо на основе экспериментальных наблюдений или нормативных данных установить среднее время ожидания очередной заявки Δ_ср. Решение этой задачи, а также обоснование функций распределения случайных величин M, L, S, r,Υ приведено в работах [13, 15].

Выбор показателя эквивалентной нагрузки лифта представляет собой самостоятельную задачу. Прежде всего необходимо определить критерий, которому должен отвечать этот показатель. Этот критерий должен быть взаимосвязан с условиями назначения или изменения периодичности ТО основных узлов лифтовой установки. Главным условием является накопленный расход ресурса узла по сравнению с его нормативным значением. Очевидно, что расход ресурса узла или детали определяется двумя факторами: временным и силовым, т. е. показатель эквивалентной нагрузки должен учитывать распределение нагрузки во времени эксплуатации так, чтобы при увеличении длительности эксплуатации и величины воспринимаемых нагрузок эквивалентный показатель возрастал. Предлагается по аналогии с оценкой нагрузки электродвигателя при длительном режиме эксплуатации с большой частотой включений в качестве показателя эквивалентной нагрузки M экв принять среднеквадратическую нагрузку за весь межремонтный период эксплуатации лифта 9 с корректировкой ее путем введения в расчет относительной частоты включений.

С учетом приведенных аргументов предлагаемая математическая модель для расчета эквивалентной нагрузки силовых элементов лифта будет иметь вид:

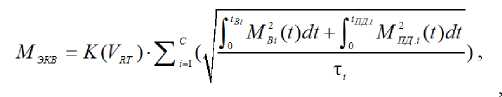
где M Bi ( t ), M _ПД .i ( t ) — соответственно моменты на валу двигателя (или в другом звене трансмиссии лифта) в функции времени t в суммарные периоды вызова лифта t Bi , перемещения t _ПД_.i кабины лифта с пассажирами;

• ⁹ Епифанов, А. П. Основы электропривода : учебное пособие / А. П. Епифанов. Санкт-Петербург : Лань, 2009. 192 с.

• τ i — продолжительность полного i-го цикла работы установки, включая продолжительность движения кабины при вызове, с пассажирами, торможении, паузах на загрузку и выгрузку пассажиров, а также ожидании очередной заявки на использование лифта, с;

С — общее количество циклов за заданный отрезок времени Т;

V _rt — частота циклов включения лифта за расчетный период T , т. е. число циклов в единицу времени, 1/ч или 1/сутки:

V — — —

^Vrt = _т =

С 1

K ( V_RT ) — корректирующий коэффициент, учитывающий частоту включения лифта; пределы изменения коэффициента K(V RT ) мин ≤ K(V RT )≤ 1 устанавливаются экспертным путем.

При частотах включения привода, близких к нормативным, K ( v _RT ) = 1 При увеличении частоты включений V _rt эквивалентная нагрузка возрастает за счет увеличения коэффициента K(V _RT ) ;

• С 1 — число включений главного привода за расчетное время Т, т. е. в периоды вызова лифта, движения с пассажирами и промежуточных остановок.

Целесообразно выделить многократно повторяющиеся массовые режимы, которые будут главным образом определять эквивалентную нагрузку за период наблюдений. Предлагается на данном этапе исследований разделить суточный период функционирования лифта в рабочие дни на четыре временных отрезка [10].

Обоснование математических моделей формирования силовых воздействий на привод лифтовой установки. Нагрузка М в период выполнения цикла работы лифта на определенном временном интервале τ i может быть представлена случайными графиками М(t) для этапов вызова и движения с пассажирами (рис. 2).

Как ранее показано, за один и тот же временной интервал между ТО лифт может совершать различное количество циклов работы, которые, в свою очередь, будут иметь различные характеристики по длительности τ i и по величине нагрузок M _экв , воспринимаемых двигателем и другими элементами лифта.

M , Hm

Нагрузка на силовой привод

Тез ;

Тдб

___ | /ТбиженсеХ | Вызоб'' X (с гпссожирели ^

t , c

Нагрузка на тормозной механизм

M, Hm t, c

Рис. 2. Цикл работы лифта: τ i — время цикла; τ _вз. i — время вызова; τ _дв. i — время движения с пассажирами; ∆ i — время, через которое поступает заявка на использование лифта после окончания цикла

На длительность выполнения заявки, величину нагрузки на привод и силовое оборудование лифта будут оказывать влияние случайные величины: M i =1, 2 …N; L i =1, 2,…N; S i =1, 2,…,N, где N — этажность дома; относительный уровень загрузки лифта по грузоподъемности; γ=Q i /Q_пасп, γ_мин<γ<γ_макс, где Q_пасп — номинальная (паспортная) грузоподъемность; интервал времени ожидания ∆ i .

Для того чтобы найти зависимость нагрузок на силовые узлы лифта от времени при воздействии перечисленных случайных величин, остановимся на определении нагрузок, которые испытывают силовые части лифтового оборудования.

Машиностроение и машиноведение

Тяговые канаты (усилие S k1 ) и канаты противовеса (усилие S п1 ) в произвольный момент времени подвергаются действиям статических нагрузок в точках набегания-сбегания с канатоведущего шкива (КВШ), которые соответствуют расчетной схеме и определяются по формулам (рис. 3):

— при подъеме-спуске кабины с _ (Ск+С$кУЗ±(Рк+Рг) ।    ,      m   Ah

^ ki           2        + л q_TK (H   ^{Ah )} g,                                 (1)

^ б

— при подъеме-спуске противовеса

5 п1 = [О н • g ± ^ п ] • Л б + И • q_TO • Ah , • g.                                     (2)

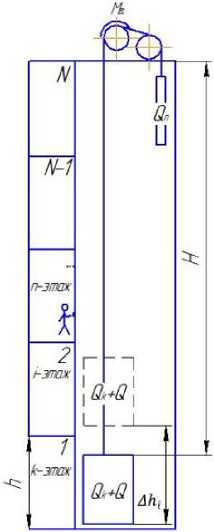
Рис. 3. Схема к расчету усилий в тяговых канатах

Знак «плюс» — при движении кабины или противовеса вверх, «минус» — при движении кабины или противовеса вниз. В формулах обозначено: Q i — масса груза в i- м цикле, кг; Q К — масса кабины, кг; Q П — масса противовеса, кг; F K — сила сопротивления движению кабины, Н; F Г — сила сопротивления движению груза, Н; F П — сила сопротивления движению противовеса, Н; η б — КПД блока канатной системы; n — число тяговых канатов; q_TK — погонная масса тягового каната, кг/м; ДК , — расстояние между уровнями первого этажа и расположения кабины с пассажирами в данный момент времени (рис. 3).

Как видно по формулам (1) и (2), натяжение ветвей тяговых канатов и канатов противовеса в точках набегания-сбегания с КВШ напрямую зависит от следующих факторов:

• —    направления перемещения кабины и, соответственно,0 противовеса;

• —    расстояния ДК , ,определяющего случайное положение и перемещения кабины. В свою очередь, изменение ДК , происходит в зависимости от случайного сочетания в данном цикле номеров этажей M i , L i , S i ;

• —    случайного значения массы перевозимых пассажиров Q i .

Помимо статических нагрузок, действующих на канаты лифта и передающихся на его приводные элементы в периоды неподвижного состояния и установившегося движения (КВШ, редуктор, двигатель, тормозное устройство), система испытывает и динамические нагружения в периоды неустановившихся движений при пусках, торможениях и др.

Типовая схема привода и трансмиссии лифта представлена на рис. 4. В данном случае рассматривается схема редукторного привода. В настоящее время получают распространение системы безредукторных приводов с двигателем, имеющим частотное регулирование для изменения скорости. Эти системы требуют отдельного исследования, выходящего за рамки настоящей работы.

Будем рассматривать совокупность кинематически соединенных элементов «двигатель — редуктор — КВШ — канаты — кабина — противовес» как систему с одной степенью свободы. В реальных условиях кабина и противовес, подвешенные на канатах, могут совершать, кроме общих, кинематически согласованных движений вместе со всеми элементами, дополнительные колебательные движения и вызывать соответствующие нагрузки в канатах и других соединенных с ними элементах.

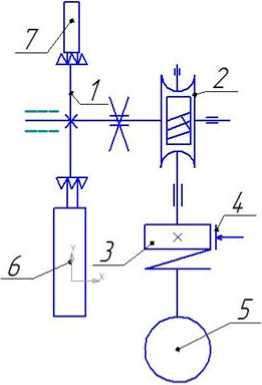
Рис. 4. Расчетная кинематическая схема лифта с редукторной трансмиссией:1 — КВШ;

2 — редуктор червячный; 3 — соединительная муфта с тормозным шкивом;

4 — колодочный тормоз; 5 — электродвигатель; 6 — кабина; 7 — противовес

Для решения такой задачи требуется представление системы привода лифта как минимум в трехмассовой постановке. Необходимо отметить, что низкочастотные колебания кабины в процессе перемещения пассажиров существенно ухудшают уровень комфортности, поэтому предусматриваются конструктивные решения, исключающие возникновение колебательных процессов.

В дальнейшем будем рассматривать совокупность взаимосвязанных частей как приведенную одномассовую систему 10 . Центром приведения принята ось вращения электродвигателя. Как видно на схеме, представленной на рис. 4, нагрузки от сил тяжести кабины и противовеса прикладываются не напрямую на электродвигатель, а передается через ряд промежуточных элементов. Таким образом, можно записать для привода лифта известное уравнение динамики электропривода 7 :

J np^ = M gB -ZM c , (3), где /пр — приведенный к валу двигателя момент инерции системы «двигатель-редуктор-ведущий шкив-канаты–кабина–противовес», кг˴м 2 ;

М дв (ω) — крутящий момент, развиваемый двигателем в функции угловой скорости, Н·м, это соотношение определяется механической характеристикой двигателя;

ΣМ _с — сумма приведенных к валу двигателя моментов сопротивлений от перемещения кабины, противовеса, канатов и потерь в передачах, Н·м.

В общем случае

^М с =Z 1 S_t • г_к/1 ред , где (4)

S i – усилие в канате в точках набегания и сбегания с КВШ, Н, определяемое по формулам (1) и (2). В этих формулах r k -радиус канатоведущего шкива, м; 1_ред - передаточное число редуктора; ю - угловая скорость двигателя, 1/с; t – текущее время, с.

Из формул (1), (2), (3) и (4) следует, что мгновенное значение суммарного момента M _дв i зависит от приведенного к валу двигателя момента инерции системы J _пр i , усилий в ветвях каната S _п1и S k1 , которые, в свою очередь, определяются сочетанием представленных ранее случайных величин M, L, S и γ.

Вместе с тем, в соответствии с целью работы необходимо установить влияние всех составляющих нагрузок и режима их формирования в целом на периодичность ТО лифта. Для этого необходимо определить так называемую представительную эквивалентную нагрузку на лифт, например, крутящий момент M экв , которая и будет величиной, оказывающей влияние на программу ТО, прежде всего на периодичность ТО. Условная ось в системе привода лифта, относительно которой вычисляется М экв , принципиального значения не имеет, т. к. с помощью известных методов приведения эквивалентная нагрузка может быть пересчитана в произвольную точку. В настоящей работе точкой приведения выбран вал главного двигателя.

Крутящий момент на валу двигателя лифта в функции времени M _д.i =f(t) на каждом отдельном этапе движения — при вызове или движении с пассажирами — определяется в результате решения дифференциального уравнения (3).

Машиностроение и машиноведение

• ¹⁰ Епифанов, А. П. Основы электропривода : учебное пособие / А. П. Епифанов. Санкт-Петербург : Лань, 2009. 192 с.

Приведенный момент инерции системы J _npi будем рассматривать в течение данного i-го цикла как постоянную величину, равную сумме моментов инерции вращающихся и поступательно движущихся масс: ротора двигателя/_дв, редуктора, включая КВШ, кабины с грузом, противовеса и ветвей канатов. Используя известное правило приведения масс и моментов инерции, получим соотношение для расчета приведенного момента инерции системы в i-м цикле работы лифта:

г2

/npi   /двКвр + [Qk + Qn + Qnacn ' Xi + Як - nk - (^   1) ' ^эт I 2,, где Квр — коэффициент, учитывающий вращающиеся массы редуктора и КВШ;

Qnacn — паспортная грузоподъемность лифта, кг;

Сумма моментов сопротивления £ М_С , приведенных к валу двигателя, при подъеме кабины:

£М_С =(г_к/1 р _е д ) (S k1 -S n1)—                                     (5)

Пред при спуске кабины:

£М с =(г_к/1 ред ) (5 п1 -5_К 1) Л ред .                                           (6)

Для расчета суммы моментов на валу двигателя значения Sk1и Sn1 необходимо подставлять из формул (1) и (2) с учетом правила знаков. При этом для случая подъема кабины с пассажирами — по формуле (5), сумма моментов будет положительной, для спуска грузов (6) — отрицательной. При подъеме кабины в формулу (5) значения Sk1и Sn1 нужно подставлять в виде:

_S k1 =    .     .   .^F _{+ п} • Я тк • (_Н - _ДЬ) • g. ₅ n1 = [Q n •g-F n ] • Л б + п • Я тк • АЬ • д.

^П б

При спуске кабины в формулу (6) значения S_n1и S_k1 нужно подставлять в виде:

S n1 = ^[Q n • g + F n ^] • Л б + п • Я тк • АЬ • g,0.

с _ ⁽ Q i +Q k ^)- g ^—(F k ^+F T ⁾ ।    ,     .ГЦ   Ahl л

^Sk1           2        ^{+ п Я} тк ^{(Н   АЬ ) g} .

^П б

В последнем случае сумма моментов сопротивлений £ М_С , рассчитанная по формуле (6), будет отрицательной, т. к. S_k1 >S_n1. При решении дифференциального уравнения (3) необходимо учитывать, что момент, развиваемый двигателем при пуске и после окончания пуска, М_дв< 0.

При решении дифференциального уравнения (3) необходимо задать начальные и конечные условия. Начальные условия для всех режимов движения с грузом или без груза одинаковы: при t=0, φ=0, ω=0. В результате решения уравнения получаем изменение момента на валу двигателя М_дв, перемещения кабины h (м), угловой скорости ω (рад/с) от времени. Рассмотрим решение уравнения (5) в целях получения функций времени М_дв, Ь, t, to.

Параметры двигателя и его механическая характеристика M дв (ω) представлены графически на рис. 5.

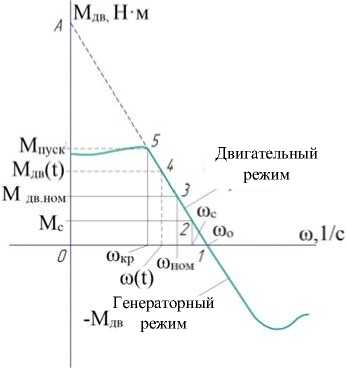
Рис. 5. Механическая характеристика асинхронного короткозамкнутого двигателя:

1 — идеальный холостой ход (синхронная угловая скорость); 2 — соответствует статической нагрузке (£ МС) в двигательном режиме; 3 — номинальной нагрузке двигателя; 4 — текущему состоянию двигателя;

5 — пусковому (критическому) режиму работы

Процесс движения в каждом цикле (с пассажирами или без них, вверх или вниз) включает в общем случае четыре этапа (рис. 6):

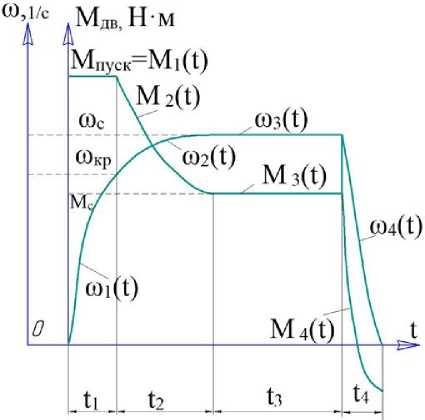
Рис. 6. Качественная картина изменения угловой скорости ω(t) и момента на валу двигателя M _дв (t) по периодам движения лифта

Необходимо отдельно рассмотреть решение уравнения при подъеме кабины £ МС > 0 (двигательный режим) и спуске кабины £ МС < 0 (генераторный режим).

Двигательный режим. На первом этапе момент, развиваемый двигателем, равен пусковому, M пуск .

Величина его сохраняется в течение всего первого периода М_дв()) = М_пуск. Уравнение (3) принимает вид: do

^;пр1 • "dt = М пуск - ^ М_С 1.

Решая дифференциальное уравнение, после преобразований получим выражения для расчета момента двигателя, времени каждого этапа и пути, проходимого кабиной. Для первого этапа:

h i

М дв1 (() = М пуск .

£   /пр1 ^ о (1 ^— ^ кр ) (^--^ ном ) ^^Мдв С^ пусК^с )

_ _ УпрЛ^О^-^ кр ) • ^(1—‘ ^ НОМ

.

^^•^•СЛ пуск ^- ^ сУ ‘ ред

)т

.

На втором этапе пуск продолжается от угловой скорости ωкр до угловой скорости ωс, соответствующей моменту статической нагрузки £МС, т. е. на отрезке юс< ю< юкр(рис. 5 и 6). Движение происходит на рабочем участке характеристики двигателя. Результаты решения и преобразований на участке 2:

М_№ 2 =М_№(а) ср) =^(1-^У ^э ном ^{4 -} ном^/

H^V^-1)];

где

^О ср 2 ⁽²    *"^кр   ^ с ^ ном ),   ^ пуск , ^- с

—

—гп^Гь h2 =-^(2, 2‘ред соответственно

отношение

пускового

момента двигателя,

статического момента сопротивления к номинальному.

По завершении второго этапа двигатель переходит в режим установившегося движения, скорость кабины определяется по формуле

^ 2 = -0-^ (1-Л с 5 ном ).                                            (7)

‘ ред

На третьем этапе происходит движение системы с установившейся скоростью, которая определяется по формуле (7). Для расчета пути третьего этапа h 3 необходимо: вычислить высоту подъёма (спуска кабины) при вызове или движении с пассажирами как разность уровней этажей (L–M)h или (M–S)h, где h — межэтажная высота; определить сумму расстояний, которые прошел лифт на первом и втором этапах: h 1 +h 2 ; вычислить путь третьего этапа: h 3 =(L–M)h–(h 1 +h 2 ).

Таким образом, получены все необходимые соотношения для силового моделирования работы лифта в

двигательном режиме.

В генераторном режиме, когда при спуске кабины с грузом, Мс<0, продолжительностью разгона можно пренебречь. Система «двигатель — редуктор — КВШ — канаты — кабина — противовес» за короткое время

Машиностроение и машиноведение

переходит в генераторный режим, двигатель создает тормозной момент, вращаясь с сверхсинхронной скоростью. Скорость спуска определяется по механической характеристике при подстановке М дв =–М с (рис. 5):

v =^(^_s +1)

• ген     1 ред    И ном ном        ^.

При расчете М_с<0 в формуле (6) необходимо вводить КПД редуктора в числитель. Зная v_reH, можно найти по аналогии с предыдущим высоту h ген и продолжительность опускания кабины на высоту Kh ген , где K — число межэтажных пролетов, проходимых лифтом.

Имитационное моделирование силовых режимов лифта выполнено по программе 11 . На рис. 7

представлены фрагменты результатов моделирования эквивалентных нагрузок. Как видно на графиках, момент на валу главного двигателя увеличивается пропорционально квадрату этажности дома и существенно зависит от времени наблюдений.

Обсуждения. Вопросы обоснования регламента ТО пассажирских лифтовых установок остаются весьма актуальными. Сущность проблемы в том, что программы ТО, рекомендуемые в нормативных документах и используемые на практике, не учитывают реальных режимов нагружения основных узлов по величине и во времени. Для воспроизводства реальных режимов лифтовых установок, функционирующих под влиянием многочисленных случайных воздействий, доказана необходимость и целесообразность имитационного моделирования.

Особенность полученных результатов исследования в сравнении с известными нормативными и литературными данными в том, что выбор регламент ТО конкретного лифта связан корреляционными соотношениями с режимными характеристиками и остаточным ресурсом установки.

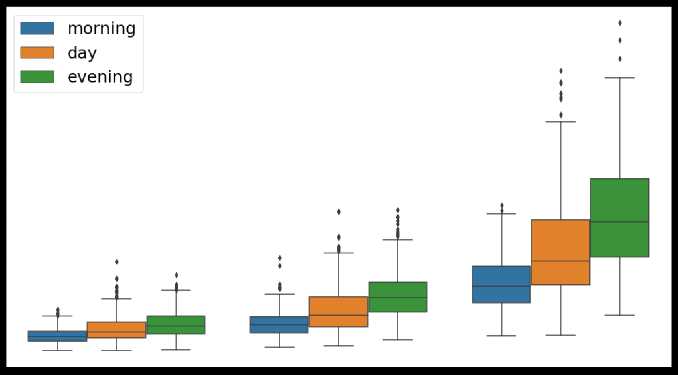
Рис. 7. Зависимости эквивалентного момента на валу двигателя лифта от этажности жилого дома (9, 16, 22 этажа) и отрезка времени наблюдений: утро (morning), день (day), вечер (evening)

Заключение. В результате исследований предложен комплексный показатель загруженности лифта, учитывающий чистое время работы, величину эквивалентной нагрузки, удельное число включений и степень отработки ресурса. В соответствии с величиной показателя определяется структура ТО. Разработаны математические модели рабочих процессов, в том числе функции распределения случайных воздействий, позволяющие осуществлять имитационное моделирование режимов работы лифтов с учетом случайного характера влияющих факторов. Детально описаны соотношения для расчета статических и динамических усилий привода лифта. Получены базовые соотношения влияния параметров лифта и условий эксплуатации на силовые и кинематические показатели лифтовой установки.