Совмещение профиля резьбы бурильной трубы с эталонным профилем

С развитием оптических измерительных приборов стало возможным проводить геометрические измерения объектов , представленных в виде совокупности точек на плоскости или в пространстве. По этим измерениям проводят совмещение с эталонными сигналами для определения геометрических параметров.

Теоретические работы по оцениванию геометрических параметров стали вестись с конца 70-х годов . Одни из первых работ были посвящены оценке параметров эллиптических профилей [1]. Однако практический интерес и, соответственно, рост публикаций по этой тематике наблюдается в последние 10-15 лет, что связано с широким распространением профильных систем для контроля геометрии объектов [2-7].

В представленной статье рассматривается частная задача, посвященная выводу алгоритма совмещения профиля резьбы буровой трубы с эталонным профилем. Данная задача возникает при оценке изношенности резьбовых соединений (например , различных видов износов, оставшегося количества скручиваний трубы, контроля осевого натяга и т.д.)

В статье использовались методы, предложенные в [8], но с учетом особенностей объекта исследования.

Постановка задачи

Профиль резьбы бурильной трубы представлен на рис . 1. Конкретные значения параметров p , a * и т.д. зависят от типа резьбы [9]. Как можно видеть из этого рисунка, на профиле можно выделить прямолинейные участки, описываемые уравнением прямых. Задачу совмещения, измеренного с эталонным профилем, можно показать на следующем примере . Пусть будут даны точки на плоскости, соответствующие измеренному профилю (см. рис . 2). Точки образуют две совокупности с координатами (р.^,) и (vJ, лежащие на различных прямых.

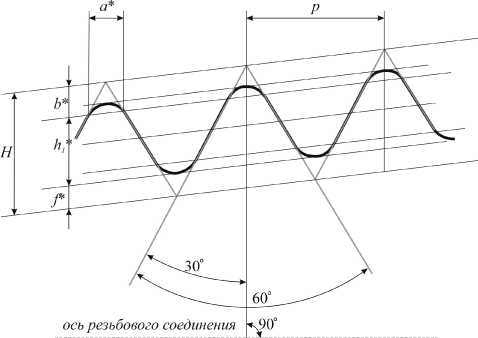
Рис. 1. Профиль резьбы

Совокупность точек Vp^ соответствует уравнению у = к_ххл-Ь_х эталонного профиля, а k>^vJ – уравнению у = k₂x + b₂ . Задача совмещения – найти так е преобразование, после которого точки {p<>y будут лежать на прямой у = к_ххл-Ь_х, а k-^vJ – на у = k₂x + b₂.

Вывод алгоритма

Согласно вышеописанному, можно записать:

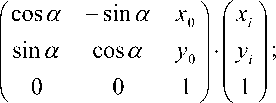
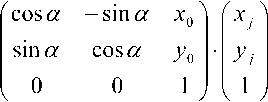
где •^ I 1 z 1 ^ «^ j      2 j ^

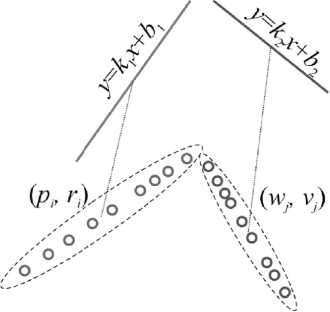
Рис. 2. К задаче совмещения профиля резьбового соединения с эталонным сигналом

Рассмотрим выражение (1), из которого можно выразить:

Xi = cosa^Pi -x₀)+ sin«(r; -_y₀);

y, =-sma{pi - x₀)+ cos a^ -y₀).

Перепишем эту систему уравнений, заменив A = cos a, В = sin a, A² +B² = 1:

^xi =Ap. -^хо)^+в^ ~Уо)’

У, =~^B{Pi -^o)+4^ -Jo)-

Подставим найденные выражения в уравнение прямой У г -klXi +^1=0, и для определения неизвестных параметров ^V0,y0J воспользуемся методом наименьших квадратов:

M В, x₀, y₀) = ^ {[- В^_{ - x₀) + Ду - д)] -- 7 Ma " v₀) + Bb - Jo)] + M ^ ^min, (3) где n – число точек;

Ш5,х0,>.„)= s +

ев 1          1

0fU.B.^y«LNiXg+Mi=Oi df(A,B,xn,y,x)                n

^{7 v} ’ °’^Ло/ = N₃ v₀ + M₃ = 0, бУо

A = X~B2 ,

^i = 2Z by - v0 + ke b - у о ))x x (^1 - АЬ -y0)+Akl (Pi - x0)),

^Mi = ²E by - ^xo + ^ki bi - Vo ))², ^2 =-²h(^B + A-kXb_x + B-_Pi-AX -j₀)+ + kU-Pi + Bb -УоЖ

M2 = 2^B + AkX , n, -г^и-вУМ-Ar,+B(_P,-x„y + k(Br. + A(p. -xj)),

М^г^А-ВкУ.

Таким образом, система уравнений запишется как:

' N_xBxM_x = 0;

Л^2 X_q + ^2 ⁼ ^ ’

TV's Уо "i” '^'з ~ 0 ’

A = bl -B2.

При выводе этой системы учитывались только точки С учетом ^j^A выражение (3)

перепишется как:

f(A, B, x0, v0) = ^ {[- B^Pi - x0) + A^ - y0)] - ki VAPi - v0)+вЬ - л)]+6i}+

+ Ё1“ ^i - Vo)+ ^(v_z - Jo )]-

7=1

- ^ki M^w₇ - v₀ )+ fib, - Jo)] + ^₂} ^ ^min • (⁵) •

Соответственно, выражение для коэффициента

^1 = ²i by - v₀ + ^кл bi - Jo)) ^x

X X - AX - Jo ) + A k, Xi - v₀)) +

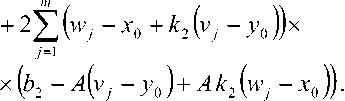
Аналогичным образом изменяются формулы для M_x; N₂ и т.д. Система нелинейных уравнений (4) решается итерационным способом, алгоритм оценивания имеет следующий вид.

• 1.    Задается первоначальное приближение: x₀,y₀,B,A = 71-5² .

• 2.    По координатам (PiP',b k’V/) и параметрам XaY b^^biY X^B,x_Q,yX рассчитываются N_X,N,,N₃,M_X,M,,M₃. '

• 3.    Рассчитываются значения В =--^,

• 4.    Присваиваем: A = A', В = В', x₀ = Xg, y₀ = Vg, a = asinXY

• 5.    Переходим к шагу №2.

^Х«⁼"^Г'^У«⁼"^Г’^Л =Yi-(b'Y ■ 7v₂              in з

Число переходов от шага №2 к шагу №5 определяет количество итераций. Аналогично тому как алгоритм проводит обработку двух совокупностей точек, он может быть расширен на три и большее их количество.

Компьютерное моделированиеи    натурные испытания

В ходе компьютерного моделирования к координатам (v,j) добавлялась помеха с гауссовым распределением и заданным СКО и по результатам работы алгоритма оценивалась среднеквадратичная ошибка. Использовались две прямые: kx = 1, bx = 0, k2 = -1, b2 = 6. Каждой прямой соответствовало 10 точек, параметры преобразования: « = 10°, x0 =20, j0 =30. Ре- зультаты точностей измерения представлены на рис. 3-4.

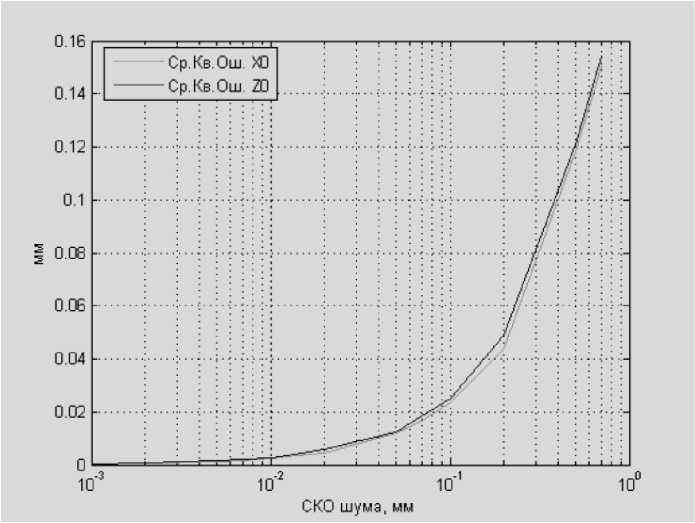
Рис. 3. Зависимость среднеквадратической ошибки измерения X ₀ , Z ₀ от шума

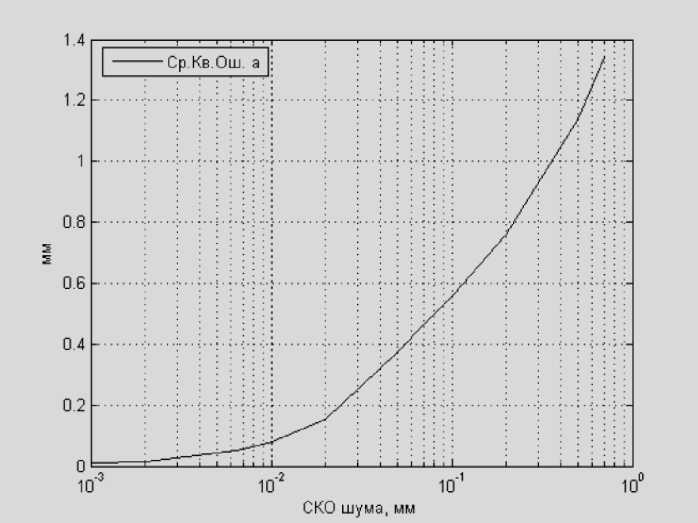
Рис. 4. Зависимость среднеквадратической ошибки измерения a от шума

На рис. 5 показан процесс получения профиля резьбового соединения бурильной трубы с использованием профильного сканера, где яркая линия на поверхности исследуемого объекта соответствует лазеру сканера.

Рис. 5. Получение профиля резьбы профильным сканером

На рис. 6 показан результат совмещения профиля резьбы с эталонным профилем в ходе натурных испытаний с использованием предложенного алгоритма.

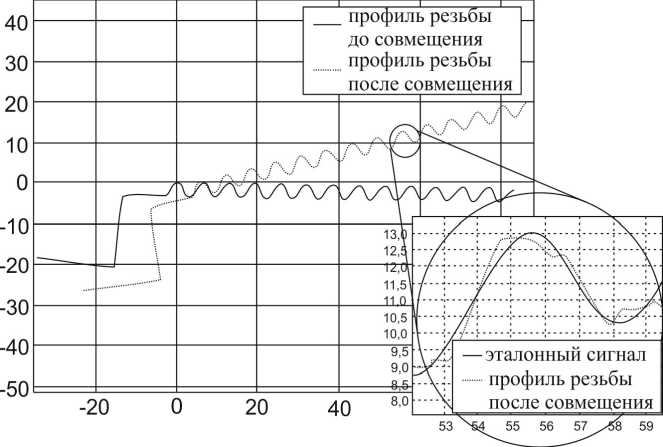
Рис. 6. Совмещение профиля резьбы с эталонным сигналом

Заключение

В работе были представлены материалы, полученные в ходе исследований сигналов профильных систем для резьбовых соединений бурильных труб. Методы оценивания для разработки алгоритма оценивания с успехом используются в теории связи уже на протяжении многих лет. Они обладают очень большой гибкостью и поэтому достаточно просто переносятся на решение задач, несколько отличных от тех, что существуют при обработке телекоммуникационных сигналов. Данная работа является продолжением [8], где использовались аналогичные способы. Последующие работы по данной тематике будут посвящены задачам совмещения профиля, отдельные участки которых описываются уравнением не только прямых, но и кривых (эллипсов, парабол и т.д.). Подобные сложные профили используются при описании профилей объектов, качество изготовления которых необходимо контролировать (например, пазы в трубах, автомобильные фары, рельсы и т.д.)