Совместная фильтрация дискретного и непрерывных 12 параметров многомерных коррелированных импульсных сигналов
Автор: Медведева Елена Викторовна, Петров Евгений Петрович, Метелев Александр Петрович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 4 т.9, 2011 года.
Бесплатный доступ
Рассмотрен синтез алгоритмов совместной фильтрации дискретного и непрерывных параметров многомерных двоичных коррелированных сигналов. Предполагается, что все параметры являются марковскими процессами. Совместная фильтрация параметров осуществляется в присутствии белого гауссовского шума (БГШ). Синтезированные алгоритмы требуют для своей реализации минимальных ресурсов и позволяют повысить помехоустойчивость приема импульсных сигналов.
Совместная фильтрация, коррелированные сигналы, марковские процессы
Короткий адрес: https://sciup.org/140191502
IDR: 140191502 | УДК: 621.391.2
Текст научной статьи Совместная фильтрация дискретного и непрерывных 12 параметров многомерных коррелированных импульсных сигналов
Введение. Постановка задачи
Синтез приемных устройств для обработки импульсных коррелированных сигналов ведется в большинстве случаев без учета взаимного влияния качества фильтрации дискретного параметра (манипулированной фазы, частоты и т.д.) на непрерывные параметры радиосигнала (амплитуда, задержка и т.д.). В действительности реализация статистической избыточности импульсных коррелированных сигналов приводит к увеличению вероятности их распознавания, что эквивалентно увеличению точности оценки непрерывных параметров при приеме некоррелированных импульсных сигналов. Задача синтеза в этом случае сводится к установлению механизма взаимодействия между устройствами фильтрации дискретного и непрерывных параметров импульсных коррелированных сигналов.
В различных постановках задача совместной фильтрации параметров бинарных импульсных сигналов, представленных простой цепью Маркова с двумя состояниями, рассматривалась в работах [1-4], в которых предполагалось, что импульсные сигналы некоррелированы. Это сужает возможности практического использования результатов работ [1-4] в системах передачи информации. Наиболее полные исследования совместной фильтрации параметров коррелированных импульсных сигналов проведены в работах [5-6].
В настоящее время наибольший практический интерес представляет совместная фильтрация параметров многомерных многоуровневых коррелированных импульсных сигналов, примером которых являются видеопоследовательности цифровых полутоновых изображений (ВП ЦПИ), представленных g -разрядными двоичными числами [7]. Совместная фильтрация дискретного и непрерывных параметров многомерных многоуровневых импульсных коррелированных радиосигналов мало изучена. Как показано в [7], ВП ЦПИ, представленные трехмерной цепью Маркова с 2g состояниями, обладают большой статистической избыточностью, реализация которой существенно увеличивает помехоустойчивость приема ЦПИ, что эквивалентно повышению точности измерения непрерывных параметров при отсутствии корреляции элементами РДИ ВП ЦПИ. Для исследования механизма воздействия оценок всех фильтруемых параметров необходима их совместная фильтрация.
Необходимо синтезировать алгоритмы совместной фильтрации дискретного и непрерывных параметров (амплитуды и задержки) многомерных двоичных коррелированных сигналов, адекватных элементам РДИ, эффективно реализующие статистическую избыточность для повышения помехоустойчивости приема многомерных импульсных коррелированных сигналов и требующие для своей реализации минимум ресурсов. Совместная фильтрация параметров осуществляется в присутствии БГШ и(0 с нулевым средним и дисперсией °" и •
Уравнения совместной фильтрации дискретногоинепрерывныхпараметров трехмерных двоичных импульсных сигналов
Разобьем g -разрядные ЦПИ, представляющие трехмерные цепи Маркова с 28 равновероятными состояниями, на g РДИ. Возьмем в качестве многомерных коррелированных импульсных сигналов трехмерные бинарные импульсные сигналы, адекватные элементам I -ых ( I e g ) РДИ ВП ЦПИ, дискретный параметр которых является трехмерной однородной цепью Маркова.
На рис. 1 представлены два соседних кадра I -ых РДИ ВП ЦПИ, разделенных на области Fqk , элементы которых являются цепью Маркова различной размерности.
Алгоритмы фильтрации элементов первых трех областей известны и хорошо изучены [7].
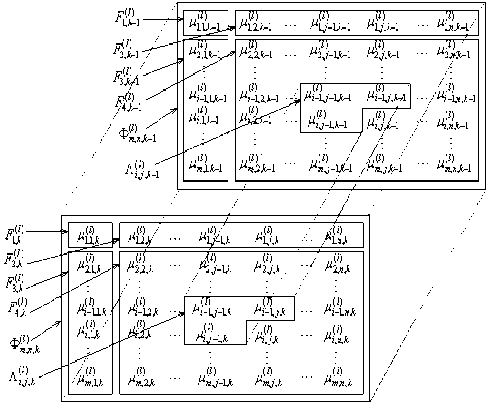
Рис. 1. Соседние кадры последовательности l -го разряда ВП ЦПИ
Наибольшую сложность представляет алгоритм фильтрации элементов области ^4k . Фильтруемый элемент ^4 ) - Hi J,к области ^4k зависит от состояний семи окрестных элементов (см. рис. 2):
^4
где
V^ uf1
r3 Hi—YJ—Y,k *>
Hi-Y,j-Y,k-\ 9
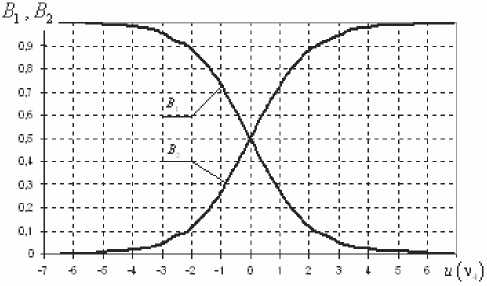
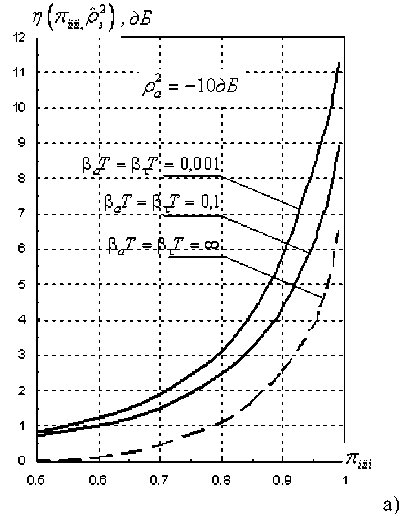
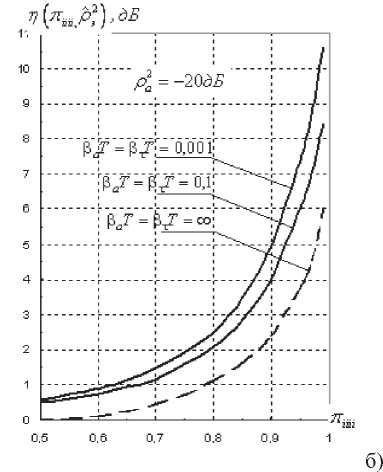
v VY Hi,j-Y,k ’ И2 Hi-YJ^k *> Hij-Y^-Y ’ Hi-Yj^-Y ’ Hij,k-Y ' Рис. 2. Фрагмент трехмерной модели l-го РДИ области ^4k Для упрощения дальнейшего изложения материала, учитывая, что алгоритмы фильтрации импульсных сигналов всех g разрядов ВП ЦПИ отличаются лишь значениями элементов матриц вероятностей переходов (МВП), индекс (/) опустим. Будем считать, что фильтрации подлежат дискретный параметр трехмерного импульсного сигнала, адекватного двоичным элементам A j к РДИ ВП ЦПИ, и два непрерывных параметра: флуктуирующая часть a амплитуды импульса А = а + о(а - среднее значение) и его задержка т. Остальные параметры полагаются априорно известными. Дискретный параметр Ц^ j к бинарных трехмерных импульсных сигналов, адекватных состояниям элементов РДИ ВП ЦПИ, представляет собой однородную трехмерную цепь Маркова с двумя равновероятными (Рх = Р^ состояниями Мх и М2 и МВП вида: а + Риа = УЛ<У ^Р^уЛ^Ь (5) где Ра ’ Pt – ширина спектров флуктуаций амплитуды и задержки соответственно; Pi (О - белый шум на единицу полосы G,, / = 1,2. Представим многомерную апостериорную плотность вероятности (АПВ) параметров трех- мерных двоичных импульсных сигналов, адекватных элементам последовательностей РДИ ВП ЦПИ, как произведение АПВ дискретного и не- "iiii "iiij ах ах ^iiji ^iijj оу а' ^ijii ^tiij аз аз Л-- Л-- «4 «4 — n = 43 х 43] = , /,7 = 1,2; i^j. (2) njiii 71 jiij а5 а5 Л1У1 Л5Щ «6 «б ЛЦп лцу ап aq \р jjji 71 jiij ) va% а'% у прерывных параметров, полагая их апостериорно независимыми [7]: к m п ^И.^гНППП^^ 9=1 /=1 >1 XPT («А )W(°|°A )X (ГА )M?(r|rA ) Матрица п симметричная и удовлетворяет условию нормировки as + a's = 1; s = 1,8. Элементы первой строки матрицы П определяются выражениями 1 7 с^ iiij У У У 2i 5 6 где 77ii | вестных элементы МВП по горизонтали, априорно из-вертикали и кадрам: п = п = 71IX Хг ^22 Если i= i = q = \, to P\u. „ 1 = 0,5 ; если z = 1,7 >1,^ = 1, TO ^{Ai./.i} = ^{а.1.|}П^{аa 1^!j} ; если z > l,y > \,q = 1 to ^{a./.i} = P{Ajj}nriw{A./.i Ki.,-i.i} ’ где 7=2 1=2 ^{Лп} _ априорная начальная трехмерная плотность вероятности; «^,.ьч \р,Н,ч ,P1-X.]-X,q,Pl-\,],q,P1J-Xfl-\,PM,H.4-' , Mi-\.j.q-\^Mi,j.q-\ \ - п = 4^2, x x и сопутствующих МВП одно- мерных цепей Маркова с двумя равновероятными состояниями : II П П; II П П; 6П= П 4П; П= П 4П = П П П. априорная условная плотность вероятности перехода от комбинации элементов окрестности Kj , к значению элемента Pui-q". a=aVV^\ ак=сУу); r=r(v4). rk = r(v,) (см. рис. 2); K(aAj аж к – апостериорные плотнос- Вычисление остальных элементов матрицы П (2) осуществляется в соответствии с состояниями элементов окрестности Л, . к . Непрерывные параметры трехмерного импульсного сигнала, адекватного элементу v4 РДИ ВП ЦПИ (см. рис. 2): флуктуирующая часть амплитуды a и задержка сигнала г независимые гауссовские марковские процессы с непрерывным пространством изменения и удовлетворяющие стохастическим дифференциальным уравнениям: ти вероятностей непрерывных параметров; w(tz|z7/(), w(r|rj – плотности вероятностей перехода непрерывных параметров. Плотность вероятности перехода дискретного параметра в (6) может быть представлена в форме их ia2)= = ^ 7T(.v^ = M^ I v^ = M^;...; v'^ = M^) x (7) x6 где М; – возможные состояния дискретного параметра г,.1 ^(') – дельта-функция. Примем для апостериорных плотностей вероятностей непрерывных параметров гауссовские распределения: где vk = РР; 0t=0(vj – апостериорные оценки флуктуирующей части амплитуды и задержки бинарных импульсных сигналов, адекватных элементам V; РДИ ВП ЦПИ; ^^i), “к =«4V^ – дисперсии апостериорных оценок непрерывных параметров импульсного сигнала в элементе V] РДИ ВП ЦПИ (рис. 2). Плотность вероятности перехода для флуктуаций амплитуды a : где ba = 1 - exp {-2 Д 7}, r - exp {-Д p. T – период тактовой частоты системы;^a=GJ^Pa – априорная дисперсия флуктуаций амплитуды. Для случайной задержки т плотность вероят- ности перехода имеет вид где br = 1 - exp (-2 Д 7} ; rr = exp {-Д p; (12) a;=Gjip – априорная дисперсия флуктуаций параметра т. Будем считать, что при наличии БГШ, искажающего изображение, функцию правдоподобия дискретного параметра сигнала для последовательности элементов РДИ можно записать в фор- ме [4]: F^Pij.k а,т к Vj.q^^ где /ур,.^0^ – логарифм функции правдоподобия элемента Pi-j-k РДИ в q -ом кадре. Подставив (7)-(11) в (6), проинтегрировав с 5 -функциями по всем элементам окрестности ^i.j.k и, при- равняв коэффициенты при одинаковых дельта-функциях ^Р^~М,), получим систему нелинейных рекуррентных уравнений совместной фильтрации дискретного и непрерывных параметров импульсных сигналов, адекватных элементам РДИ ВП ЦПИ: где ^тк ^r ^k "+" 6r ^r ’ ^ak ^ a ^k ~*~ ^a ^a ’ к+1 4 ) ^ к 4*1 4 ) ^ к ci к – экстрапо лированная оценка флуктуирующей части амплитуды импульсного сигнала элемента V] РДИ ВП ЦПИ;®A=rA– экстраполированная оценка задержки импульсного сигнала элемента vt РДИ ВП ЦПИ, c – коэффициент нормировки. Будем считать, что флуктуации амплитуды сигнала малы, то есть выполняется условие ^»a и p; =^«1. Тогда, проинтегрировав уравнение (14) по непрерывным параметрам, разделив полученное выражение с v4 = Mt на выражение с v4 = M и прологарифмировав, получим рекуррентный алгоритм нелинейной фильтрации дискретного параметра бинарных трехмерных импульсных сигналов, адекватных элементам РДИ ВП ЦПИ в виде: M(v4) = [/(Mi WX A4)-/(^2(v4),(; ,®t)] + +[ф(аЬ)аа,0,)-ф(л^2(у4),^ ,©,)]+ +m(v, ) + z, [m(v, ),'я-..] + и(у2) + +z2[m(v2),2«-,7] + m(v4 ) + z4^(v; ),X]+ (15) +m(v3' ) + z7[m(v( ),A.-]-l/(v3)- -z3[г/^рл-,.]-^,' )-z5[m(v; ),p]- -Mp )-z6[«(v' ),6л-..]>Я, где – логарифм отноше- Рг (^4 ) ния АПВ состояний элемента v4 (см. рис. 2); / м>4 л A – логарифм функции прав- доподобия дискретного параметра м, в экстраполированной на такт точке оценки амплитуды и задержки сигнала в элементе Vj РДИ ВП ЦПИ; H – порог, минимизирующий ошибки различия бинарных сигналов по критериям идеального наблюдателя [1]; где ^"тг7– коэффициент, определяющий ши- 1 yo рину спектра единичного импульсного сигнала. Запишем уравнение для апостериорной оценки задержки ®A- + 1 и ее нормированной на <7^ дисперсии ^4+1 в виде: "r (•) =ln -,C) = ln X + X/exP{-MW X + '^,,exp{M(vz)} r/r,+ Xvexp|-«(v; ) г^ + 'Х,ехр{м(1Д )} r ли (z = 1,2; r = 1,7) – элементы МВП в одномерных цепях Маркова с двумя состояниями; ; q = 1,3; r = 1,3; (16) ;= 1,4;/•= 4,7; (17) Вычислим логарифм функции правдоподобия дискретного параметра сигнала: ^/(w^X Aj „ _ A1! где – оценка отношения сигнал/шум в О A A / , _ A единичном импульсе; A = AlvT j = a + Kt – экстраполированная оценка амплитуды в элементе v, РДИ в q -ом кадре ВП ЦПИ (см. рис. 2). Для импульсов гауссовской формы нормированная автокорреляционная функция имеет вид где T, – эффективная длительность единичного импульса. При малой апостериорной неточности измере ния задержки величина мала, поэтому экспоненту в правой части (20) можно разложить в ряд Тейлора и ограничиться двумя членами разложения причем 5, + S, = 1, p"T = —^ . На рис. 3 представлены графики изменения коэффициентов Bx ,B, . Рис. 3. Значения коэффициентов Bx и B-, Первый сомножитель в знаменателе (23) представляет собой сумму экстраполированной на такт апостериорной и априорной дисперсии задержки, а второй равен обратной величине дисперсии единичного замера на выходе дискриминатора задержки, то есть второе слагаемое в знаменателе (23) есть не что иное, как отношение двух дисперсий задержки. Уравнение для оценки флуктуирующей части амплитуды сигнала при гауссовских флуктуациях: vw = ^ + Xw ^81 (Z1 -a- Vk ) + B2{f2-a- Vk )] , (25) гДеХм = b,P>k;Xk x^baP>k;xk < “к zk =—■ О" (Т Будем считать, что используются ФМ импульсные сигналы, для которых л=-л- Пренебрегая шумами измерения задержки по сравнению с БГШ, окончательно алгоритм фильтрации дискретного параметра двоичного сигнала можно представить в виде +m(v' ) + z4(w(v' ),y) + «(v; ) + z7(m(tV )>Х)- (29) -m(v,)-z3 (и(и.),у j-z/^' )-z5(z/(v,' ),"X)- -»(V2 )--6(»(V2 )/\)^Я- Если шумы на входе приемника малы, то, пренебрегая шумовым членом в квадратной скобке (29) и используя разложение (21), получим = 4/77. (30) Из (30) следует, что добавка к сигнальной части ц©к-^ позволяет скомпенсировать уменьшение отношения сигнал/шум на выходе приемного устройства, вызванное незнанием истинного значения задержки. Результаты исследования На рис. 4 представлен выигрыш по мощности п^ни,р-^ при совместной оптимальной фильтрации дискретного и непрерывных параметров (амплитуды и задержки) сигнала. Сплошными линиями обозначены графики выигрыша при наличии каналов измерения задержки и амплитуды, пунктирными – при их отсутствии. Отношение сигнал/шум на входе приемного устройства У =-ЗдБ (см. рис. 4а; б). Статистическая избыточность трехмерных коррелированных импульсных сигналов, адекватных элементам РДИ ВП ЦПИ, даже при относительно небольшой корреляции по каждому измерению х = 0,8 (z = l,2; r = l,g) имеет большую величину (^ш = 0,99), реализация ко- торой в условиях флуктуирующей амплитуды и случайной задержки дает выигрыш по мощности сигнала до 12 дБ и мало зависит от Ра . Рис. 4. Выигрыш в отношении сигнал/шум на выходе приемного устройства На рис. 5 показан пример нелинейной фильтрации ВП ЦПИ «Самолет» из 5 кадров размером 1300x800. На рис. 5а приведен незашумленный первый кадр ВП ЦПИ, а на рис. 5б – тот же кадр, зашумленный БГШ при Рвх = На рис. 5в; г представлены отфильтрованные 1-ый и 5-ый кадры ВП ЦПИ при отсутствии каналов измерения задержки и амплитуды, на рис. 5д;е – отфильтрованные 1-ый и 5-ый кадры ВП ЦПИ при наличии каналов измерения задержки и амплитуды. Рис. 5. Совместная нелинейная фильтрация ВП ЦПИ при наличии каналов измерения задержки и амплитуды Из приведенных результатов следует, что учет при фильтрации дискретного параметра импульсных сигналов каналов измерения задержки и амплитуды позволяет повысить качество приема ВП ЦПИ. Заключение Результаты исследования совместной нелинейной фильтрации дискретного информационного и непрерывных параметров многомерных импульсных сигналов, адекватных элементам РДИ ВП ЦПИ, показали, что совместную фильтрацию параметров импульсных сигналов имеет смысл производить для коррелированных сигналов, содержащих большую статистическую избыточность, которая при ее эффективной реализации может значительно повысить помехоустойчивость приема импульсных сигналов.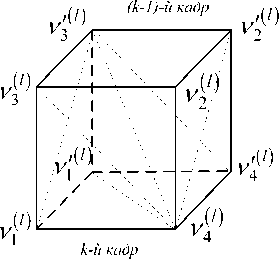
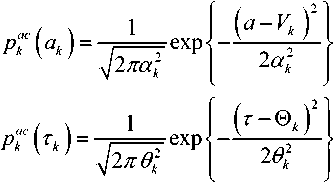
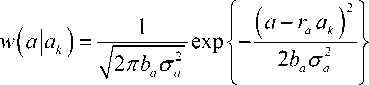
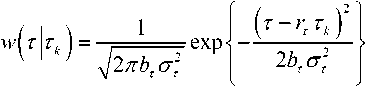
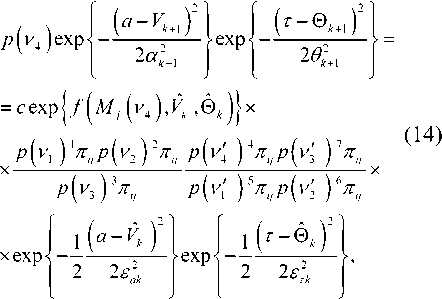
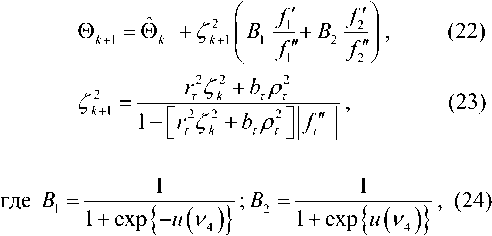
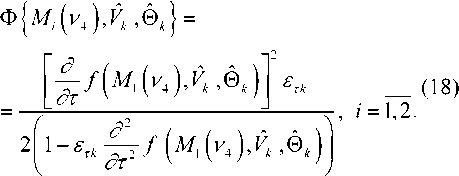
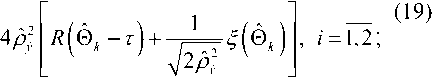
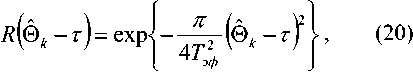
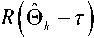
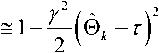
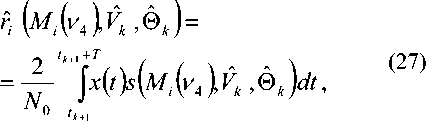
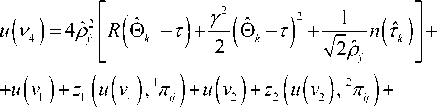
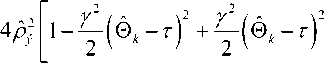

Список литературы Совместная фильтрация дискретного и непрерывных 12 параметров многомерных коррелированных импульсных сигналов
- Тихонов В.И., Степанов А.С. Совместная фильтрация непрерывных и дискретных марковских процессов//Радиотехника и электроника. №7, 1973. -С. 1376-1383.
- Ярлыков М.С., Миронов М.А. Повышение эффективности и качества систем синхронизации за счет использования информационной избыточности//Радиоэлектроника. Труды вузов Лит.ССР. Синхронизация систем связи. №19(3), 1983. -С. 72-77.
- Трифонов А.П., Шинаков Ю.С. Совместное различение сигналов и оценка их параметров на фоне помех. М.: Радио и связь, 1986. -264 с.
- Амиантов И.Н. Избранные вопросы статистической теории связи. М.: Сов. радио, 1971. -416 с. «Инфокоммуникационные технологии» Том 9, № 4, 2011 19
- Петров Е.П. Совместная фильтрация дискретного и непрерывных параметров двоичных коррелированных сигналов//Труды IV МНТК Радиолокация, навигация, связь. Воронеж, 1998. Т.1. -С.46-53.
- Петров Е.П., Прозоров Д.Е., Кишмерешкин П.Н. Совместная фильтрация параметров импульсных коррелированных сигналов с не известной амплитудой и задержкой//Труды VII МНТК Цифровая обработка сигналов и ее применение. М., 2005. Т.1. -С. 243-247.
- Медведева Е.В., Метелев А.П., Петров Е.П., Трубин И.С. Нелинейная многомерная фильтрация цифровых полутоновых изображений//Труды XI МНТК Радиолокация, навигация, связь. Воронеж, 2009. Т.1. -С. 182-192.


