Совместная реконструкция и сегментация изображений: сравнение двух алгоритмов малоракурсной томографии

algorithm, FISTA) [21], позволяет получить точную реконструкцию всего по 15 ракурсам (FORBILD фантом головы), а алгебраический алгоритм реконструкции с регуляризацией посредством минимизации нормы полной вариации (algebraic reconstruction technique with total variation (TV) regularization, ART-TV) [22,23] – по 20 ракурсам (фантом Шеппа–Логана). Интенсификация исследований в области FVT способствовала выявлению целого ряда практических немедицинских приложений томографии, где желаемым стало получение точной реконструкции по еще меньшему числу ракурсов (7–9). К таким приложениям можно отнести контроль багажа в аэропортах [24], эмиссионную томографию плазмы [25], томографию сборок тепловыделяющих элементов [26], электронную томографию наноматериалов [27], томографию сильно поглощающих сред [28,29] и пр. В свете изложенных обстоятельств авторам настоящей статьи, которые работают в области последнего из названных приложений, актуальной виделась разработка такого алгоритма FVT, который бы позволил осуществить еще один качественный переход: от точной реконструкции по 15–20 ракурсам к точной реконструкции по 7–9 ракурсам. Опыт алгебраической реконструкции [29–33] и построения масок изображений [34–36] позволил нам предположить, что подобная задача может быть решена посредством дополнения алгоритма ART-TV эвристической процедурой сегментации и организации цикла, в котором

ART-TV и алгоритм сегментации будут работать последовательно один за другим. Такой гибридный алгоритм был нами разработан и получил название ART-TVS (ART-TV с сегментацией). Уже первые результаты, казалось бы, превзошли все наши ожидания: удалось получить точные реконструкции модели обжатой взрывом металлической оболочки по 8 ракурсам, а модели газодинамической среды – по 4 ракурсам. Эти результаты были представлены на Международной конференции «XIII Забабахинские научные чтения» (Снежинск, Россия, март 2017 г.) [37], получили высокую оценку участников конференции и расценивались нами как революционные. Однако проведенный позже более скрупулёзный анализ зарубежных литературных источников столкнул нас со статьей Стората и соавт. [38], где была представлена точная реконструкция фантома Шеппа–Логана всего по 7 ракурсам. Более того, авторами указанной статьи утверждалось, что их итерационный алгоритм минимизации функционала Поттса (iterative Potts minimization algorithm, IPMA), подобно нашему ART-TVS, выполняет совместную реконструкцию и сегментацию изображений. В создавшейся ситуации возникло естественное побуждение сравнить эти два алгоритма (IPMA и ARTTVS) и выявить, какой из них и по каким критериям превосходит другой. Результаты подобного исследования представлены в настоящей статье.

Статья организована следующим образом. В параграфе 1 дано описание и качественное сравнение алгоритмов IPMA и ART-TVS. Постановка и результаты численного эксперимента по реконструкции двух 2D-моделей: фантома Шеппа-Логана и QR-кода с использованием двух указанных алгоритмов, а также их сравнительный количественный анализ представлены в параграфе 2. В заключении дано обобщение полученных результатов, сформулированы выводы и обозначены направления дальнейших исследований.

1.    Описание и качественное сравнение алгоритмов

В настоящей статье ставится и решается задача реконструкции кусочно-постоянного изображения, описываемого вектором f = { f j } J ( J - число пикселей изображения). Далее вектор f мы будем условно называть изображением. Модель кусочно-постоянного изображения хорошо подходит для рентгеновской компьютерной томографии, информативный параметр которой – линейный коэффициент ослабления приблизительно одинаков в различных однородных областях объекта. В случае малого числа ракурсов задача сводится к решению сильно недоопределенной системы линейных алгебраических уравнений

Wf = g , (1) где g = { g i } I - вектор проекционных данных ( I - число лучей, соединяющих источники и детекторы), а W = { W j } 1J - матрица весовых коэффициентов, которые рассчитываются классическим образом [2, 3], как длины отрезков пересечения лучей с пикселями изображения.

Алгоритм IPMA

Алгоритм IPMA решает оптимизационную задачу Поттса [38, 39], которая ставится в виде

||V f| |0 ^ min s.t. Wf = g ,                      (2)

где ||Vf||0 - L о - норма изображения V f , а оператор набла V в данном случае обозначает дискретное градиентное преобразование f . Как известно, L 0 – норма изображения – это число его ненулевых пикселей. Дискретное градиентное преобразование кусочнопостоянного изображения представляет собой разреженное изображение, ненулевые пиксели которого образуют границы структур изображения исходного (см., например, [22]). Таким образом, решение задачи (2) подразумевает условную минимизацию полной длины всех границ исходного кусочно-постоянного изображения. Задача минимизации решается методом неопределенных множителей Лагранжа. При этом функционал Лагранжа (он же функционал Поттса) записывается в виде [38, 39]

• P , ( f ) = | |Wf - g| |2 +y||V f| ^                           (3)

где ||Wf - g| |2 - L ₂ - норма (Эвклидова норма) невязки проекционных данных g , а у - параметр регуляризации (он же множитель Лагранжа).

Алгоритмически задача минимизации функционала (3) решается посредством организации итерационного процесса, где на каждой ( n + 1)-итерации выполняется последовательность следующих операций [39]. Во-первых, определяется вспомогательное изображение f ⁽ n ^{+ 1)} размера f по формуле

• f ⁽ n ^{+ 1)} = ( I - W * W ) f ⁽ n ) + W * g ,                      (4)

где I – единичная матрица, W ^* – комплексно-сопряжённая матрица. Во-вторых, методом динамического программирования решается классическая задача Поттса, характерная для процедуры удаления шума или блюринга изображения,

• f ^{( n + 1)} = arg min | |f - f ^{( n + 1)}|| +y||V f||0 .                     (5)

Метод динамического программирования, основная идея которого состоит в решении задачи путем ее разбиения на подзадачи, рекуррентно связанные между собой, кратко описан в статьях авторов IPMA [38,39]. За более подробным описанием метода мы отсылаем читателей к статье Мамфорда и Шаха [40]. Итерации повторяются до полной сходимости алгоритма. Критерием выхода из итерационного цикла является достижение заданного значения s отношением

II f ( n + 1) - f ( n )||

II f^{( n +1}1+1 f^{( n} )IL      ,                                          ⁽⁶⁾

которое в [39] условно названо «относительным L 2 – расстоянием» между двумя соседними приближениями решения.

IPMA реализован авторами статей [38,39] кодом в среде MATLAB, который находится в открытом до- ступе в сети Internet [41]. Этот код мы и использовали в нашем численном эксперименте (см. параграф 2) для получения результатов реконструкции тестовых моделей с помощью IPMA. При этом мы варьировали параметр регуляризации γ в пределах [0,005; 0,5]. Наилучшие результаты, представленные в параграфе 2, соответствуют значению γ = 0,01 в случае реконструкции фантома Шеппа–Логана и значению γ = 0,04 – в случае восстановления QR-кода. Параметр останова итерационного цикла ε был выбран равным значению 10 -6 в соответствии с рекомендациями [39].

Алгоритм ART-TVS

Наш алгоритм ART-TVS задуман как улучшенная модификация ART-TV и включает две стадии. Первая стадия – это собственно ART-TV в версии авторов статьи [23]. Вторая стадия – это эвристическая процедура сегментации, реализованная с использованием известного метода наращивания областей [42]. Далее мы организуем цикл, в котором эти две стадии работают последовательно одна за другой. На ART-TV стадии уже осуществляется выбор дискретных значений, которые должны определить кусочнопостоянную структуру изображения. Однако в случае малого числа ракурсов TV-регуляризация не справляется с задачей правильного выбора дискретных значений, в результате ART-TV сходится к неверному решению. Введение нами в алгоритм стадии сегментации призвано упорядочить процедуру выбора правильных дискретных значений реконструируемого изображения и, таким образом, добиться эффекта дополнительной регуляризации процесса алгебраической реконструкции. Особенностью нашего алгоритма ART-TVS является тот факт, что после сегментации мы далее применяем алгоритм ART-TV посег-ментно, обрабатывая не все изображение сразу, а последовательно выбираемые сегменты из сформированного списка сегментов. Таким образом организуется цикл еще и по сегментам. С учетом сказанного последовательность шагов алгоритма ART-TVS может быть представлена следующим образом.

Шаг 1. Восстановить изображение с помощью алгоритма ART-TV.

Шаг 2. Применить к полученному изображению метод адаптивной сегментации и сформировать список сегментов, подлежащих дальнейшей обработке.

Шаг 3. Выбрать случайным образом необработанный сегмент из списка сегментов.

Шаг 4. Восстановить выбранный сегмент с помощью алгоритма ART-TV. При этом в пиксели, принадлежащие другим сегментам, поправки не вводятся.

Шаг 5. Удалить обработанный сегмент из списка сегментов.

Шаг 6. Если список сегментов не пуст, то перейти на шаг 3, иначе – на шаг 7.

Шаг 7. Проверить стоп-критерий. Если он не выполняется, то перейти на шаг 2. В противном случае закончить выполнение алгоритма.

В качестве стоп-критерия мы используем скорость сходимости итерационного процесса. Т. е. цикл прерывается, когда достигается заданное значение v скорости

II Wf ^{( z )} - g ₂ - Wf ^{( z + 1)} - g ₂

II Wf ( z ) _-g I 2

≤ν ,

где z – индекс итераций внешнего цикла ART-TVS. При проведении численного эксперимента, описанного в параграфе 2, значение v варьировалось в пределах от 0,0005 до 0,001. В ряде случаев итерации приходилось продолжать и после достижения скоростью сходимости заданного значения с тем, чтобы улучшить результат реконструкции. Тогда в силу вступал критерий визуального сходства восстанавливаемого изображения и исходной модели.

На ART-TV стадии реконструкции (шаги 1 и 4 алгоритма ART-TVS) ставится и решается следующая оптимизационная задача

IIf _TV → min s. t. Wf = g , (8) где || f || _TV – норма полной вариации (TV-норма) изображения f . Эта норма представляет собой не что иное, как L 1 – норму дискретного градиентного преобразования изображения f , т.е. || f || TV ≡∇ fII ₁ . Таким образом, ART-TV, так же как и IPMA, представляет собой CS-алгоритм, ориентированный на реконструкцию кусочно-постоянных изображений, которые переводятся в разряд разреженных посредством дискретного градиентного преобразования. Задача минимизации (8) решается неявно посредством реализации двух раздельных шагов, которые при необходимости циклически повторяются. На первом шаге (ART-шаге) выполняются стандартные итерации алгебраической реконструкции в соответствии с формулой [2, 3]

g i - ∑ W ij f j ^{( k )} f j ^{( k + 1)} = f j ^{( k )} +λ^{∑ j} ₂ W ij , (9)

∑ j Wij где k – индекс итерации, λ – управляющий параметр, i = 1,2, ..., I; j = k mod J + 1. На втором шаге (TV-шаге) TV-норма полученного изображения минимизируется с применением стандартного алгоритма наискорейшего спуска, выполняющего градиентные итерации в соответствии с формулой [23]

f ( s + 1) ₌ f ( s ) _-τ ^∂ || f ^{( s )} || TV ^jj    ∂ f j

,

где s – индекс итерации, τ – шаг итерации. Для вычисления нормы || f(s)||TV и ее градиента ∂|| f(s)||TV ∂fj мы используем приближенные формулы сглаженной изотропной версии ART-TV, подробно описанной в статье Юу и соавт. [23]. Далее организуется цикл, в котором ART-шаг и TV-шаг последовательно чередуются. Итерационный процесс управляется оператором и прекращается, когда изображения, полученные на двух соседних итерациях, становятся визуально неотличимыми друг от друга. Реально число внутренних итераций ART- и TV-шагов не превышает 5, а число итераций ART-TV цикла – 50. Поэтому наш алгоритм ART-TVS, несмотря на наличие нескольких внутренних циклов, оказывается конкурентноспособным и даже выигрывает у IPMA в скорости реконструкции (см. параграф 2). Что касается управляющих параметров алгоритма ART-TV, то параметр λ выбран на основании нашего опыта алгебраической реконструкции [29–33] равным λ = 0,9, а шаг итерации τ подстраивается на каждой итерации в соответствии с алгоритмом, описанным в [23]. Начальное значение шага итерации также выбрано в соответствии с рекомендациями, сделанными в указанной статье: τ0 = 0,997.

Как отмечено выше, стадия адаптивной сегментации (шаг 2 алгоритма ART-TVS) реализуется с использованием метода наращивания областей. На данном этапе исследований мы не ставили целью разработать оптимальный с точки зрения минимизации числа ракурсов алгоритм сегментации. Цель была – выбрать из существующих алгоритмов сегментации наиболее простой и стабильный алгоритм, но при этом минимально зависимый от интерактивного вмешательства оператора. Требование адаптивности к алгоритму сегментации обусловлено желанием максимально сократить время работы алгоритма ARTTVS, в цикле которого процедура сегментации должна повторяться многократно. Как известно, стандартная реализация метода наращивания областей [42] зависит от выбора начальной точки наращивания. Наиболее простой и эффективный путь избавиться от этой зависимости и сделать алгоритм адаптивным – это рандомизировать выбор начальной точки [43]. Мы пошли именно этим путем.

Таким образом, мы инициируем точку (пиксель) наращивания случайным образом. Все пиксели полученного сегмента исключаются из массива необработанных пикселей изображения. Следующий пиксель выбирается также случайным образом из оставшихся необработанных пикселей. Процедура повторяется до тех пор, пока остается хотя бы один необработанный пиксель. На основании сказанного наш алгоритм адаптивной сегментации может быть представлен следующей последовательностью шагов.

Шаг 1. Случайно выбрать пиксель из множества необработанных пикселей сегментируемого изображения.

Шаг 2. Применить алгоритм наращивания областей в реализации, описанной в статье Менерта и Джеквея [42].

Шаг 3. Пометить пиксели полученного сегмента как обработанные.

Шаг 4. Если есть еще необработанные пиксели, перейти на шаг 1. В противном случае закончить выполнение алгоритма.

Значение порога при выполнении шага 2 задается оператором, исходя из особенностей сегментируемого изображения. Для описанного ниже численного эксперимента порог находится в пределах от одного до десяти процентов максимальной интенсивности изображения.

Обе стадии алгоритма ART-TVS реализованы авторами настоящей статьи кодом в среде MATLAB.

Качественное сравнение алгоритмов

Как пишут в [38] сами авторы IPMA, их алгоритм можно качественно характеризовать с двух сторон. С одной стороны, IPMA решает обратную задачу относительно кусочно-постоянной функции, т.е. выполняется реконструкция изображения. С другой стороны, в результате работы алгоритма образуется фрагментарная структура, каждый фрагмент (или сегмент) которой характеризуется своим собственным значением интенсивности, т.е. выполняется сегментация изображения. Однако совершенно очевидно, что IPMA в ходе итерационного процесса (4)–(5) не сегментирует изображения в явном виде. Сегментация как бы скрыта внутри алгоритма реконструкции и является следствием решения обратной задачи. При этом фрагментарная структура образуется, как мы увидим из дальнейшего рассмотрения, независимо от того, к правильному или неправильному решению алгоритм сходится. Таким образом, авторы IPMA вполне обоснованно утверждают, что их алгоритм выполняет «совместную реконструкцию и сегментацию изображений». В отличие от IPMA алгоритм ART-TVS сегментирует промежуточные результаты реконструкции в явном виде. Сегментация искусственно вводится в алгоритм с тем, чтобы усилить эффект TV-регуляризации с целью синтеза «правильной» фрагментарной структуры. При этом реконструкция и сегментация последовательно сменяют друг друга внутри итерационного цикла. Поэтому ART-TVS в отличие от IPMA было бы корректнее назвать не алгоритмом, выполняющим совместную реконструкцию и сегментацию, а алгоритмом, сочетающим эти две процедуры.

Теперь о возможности обоснования сходимости алгоритмов. IPMA ставит и решает оптимизационную задачу реконструкции (2) в явном виде. По этой причине представляется возможным строго доказать сходимость алгоритма, что и сделано его авторами в статьях [38,39]. Алгоритм ART-TVS минимизирует, как мы полагаем, TV-норму изображения, но делает это неявно. Строго доказать сходимость нашего алгоритма в силу того, что в него включена эвристическая процедура сегментации, представляется затруднительным. Опосредованно же объяснить сходимость ART-TVS можно, например, следующим образом. Алгоритм ART-TV ставит и решает оптимизационную задачу (8). Он сходится. Это доказано строго в [23]. Мы вводим сегментацию для того, чтобы улучшить фрагментарную структуру, которая получается в результате работы ART-TV. Таким образом, нужно убедиться в том, что действительно происходит улучшение, а не ухудшение. Это можно сделать посредством сравнения результатов, полученных на различных итерациях ART-TVS. В качестве примера на рис. 1 сравниваются фрагменты промежуточных результатов реконструкции фантома Шеппа–Логана, соответствующие 5-й (рис. 1в и 1г), 15-й (рис. 1д и 1е) и 30-й (рис. 1ж и 1з) итерациям ART-TVS. Левый столбец фрагментов (рис. 1в, 1д и 1ж) представляет результаты, полученные после работы ART-TV, но до применения процедуры сегментации, а правый столбец (рис. 1г, 1е и 1з) – это уже фрагменты сегментированных изображений. Мы видим, что после сегментации фрагменты приобретают выраженную «пятнистую» структуру, свойственную сегментированным изображениям. При этом хорошо заметно, что после 15-й итерации фрагментное изображение (рис. 1е) получилось более близким к оригиналу (рис. 1б), чем после 5-й (рис. 1г), а после 30-й (рис. 1з) – более близким, чем после 15-й (рис. 1е). Что наглядно подтвер-

ждает сходимость нашего алгоритма.

а)

б)

в)

д)

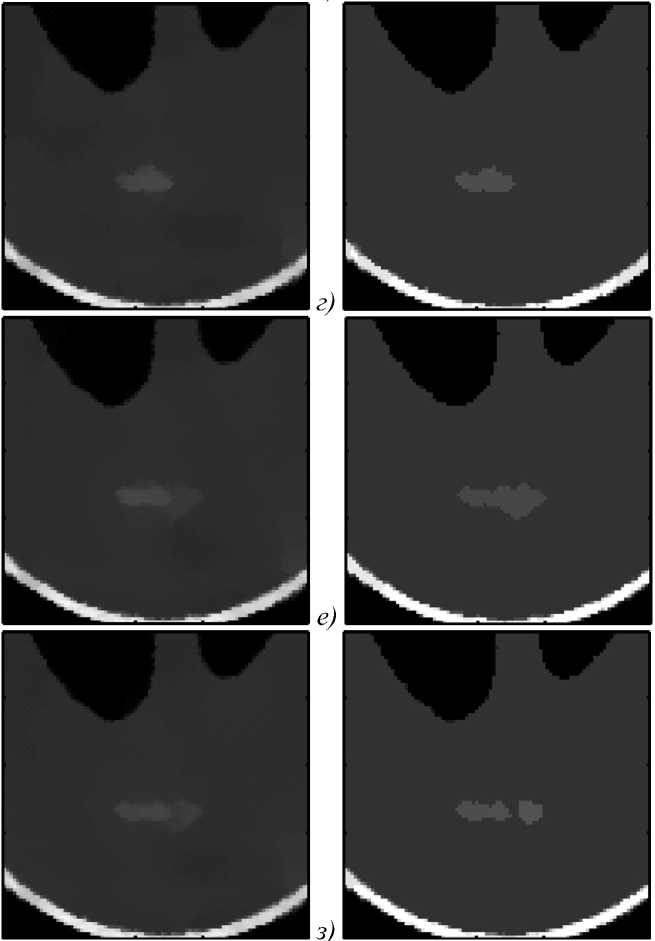
Рис. 1. Фантом Шеппа–Логана, заданный на сетке

256 х 256 (а); увеличенный фрагмент фантома (б); фрагменты промежуточных результатов реконструкции фантома до (слева) и после (справа) сегментации, соответствующие 5-й ((в) и (г)), 15-й ((д) и (е)) и 30-й ((ж) и (з)) итерациям ART-TVS

2. Численный эксперимент и анализ его результатов

Для того чтобы сравнить алгоритмы IPMA и ARTTVS количественно, нами поставлен численный эксперимент по реконструкции двух 2D-моделей: фантома Шеппа–Логана и QR-кода текста «Совместная реконструкция и сегментация изображений» (рис. 2). Фантом Шеппа–Логана, как известно, является «золотым стандартом» при тестировании алгоритмов реконструкции. А QR-код выбран нами как объект, точная реконструкция «тонкой» высокочастотной структуры которого представляет собой задачу повышенной сложности. Идея выбрать именно такой объект для исследования алгоритмов заимствована нами из статьи [44]. Моделировалась веерная геометрия съема данных: расстояние между источником и центром объекта – 70 у.е.д. (условных единиц длины), расстояние между источником и линейкой детекторов – 125 у.е.д. Область реконструкции – квадрат со стороной 6 у.е.д. Расстояние между центрами соседних детекторов выбрано равным 0,02 у.е.д. Число детекторов линейки равно 500. Схема расположения источников вокруг объекта – полукруговая с равным угловым шагом между ракурсами. Проекционные данные, по которым восстанавливались томограммы моделей, моделировались посредством вычисления сумм

J gh =£wjfl, h=1,2;                       (ii)

j = 1

где f h = { f jh } J - вектора, описывающие исходные модели, h – индекс модели. Для того чтобы исключить «инверсное преступление» (inverse crime) [45], все расчеты прямой задачи (11) выполнены для матрицы 1000 х 1000. В то время как томограммы фантома Шеппа–Логана восстанавливались на матрицы 256 х 256 и 500 х 500, а томограммы QR-кода - на матрицы 228 х 228 и 513 х 513.

Рис. 2. Тестовые модели, заданные на сетке 1000 х 1000: фантом Шеппа–Логана (а), QR-код (б)

В качестве характеристик качества реконструкции, позволяющих оценить, насколько точно удается восстановить исходные численные модели, мы выбрали коэффициент корреляции k cor и показатель отклонения k dev :

ж)

k cor

£( ГТ - Г” )( fsr - rr j = 1

( J - 1) А f^{t om} А f ^sc

kd ev

J 7 1 ( f tom - fr ) ²

V J j = 1

А f ^sc

где f и Af- среднее значение и среднеквадратическое отклонение, вычисленные по всем J ячейкам изображения, а индексы «src» и «tom» обозначают отношение к исходной модели и реконструированному изображению соответственно. Наш опыт (см., например, [36]) свидетельствует об удобстве и эффективности использования этих характеристик в тех случаях, когда исходная модель известна. Значение kcor, близкое к единице, показывает высокую корреляцию между исходной моделью и реконструированным изображением и свидетельствует о высокой точности реконструкции. Значение kdev, близкое к нулю, говорит о хорошем совпадении двух изображений и также характеризует высокую точность реконструкции. Если же значение kcor ближе к нулю, чем к единице, а значение kdev близко или превышает единицу, значит, мы восстановили изображение плохого качества.

Результаты реконструкции моделей с использованием алгоритмов IPMA и ART-TVS по идеальным проекционным данным (11) приведены на рис. 3–5, а по зашумленным проекционным данным – на рис. 6 и 7. Шкала интенсивности изображений во всех случаях проградуирована в обратных у.е.д. Значения характеристик качества (12) и (13), рассчитанные для всех томограмм рис. 3–7, приведены в табл. 1.

Табл. 1. Характеристики качества изображений, представленных на рис. 3 – 7

Рис.	Фантом	Алгоритм	Число ракурсов	Сетка	Шум, %	K cor	k dev
3 а	Шеппа– Логана	IPMA	7	256 х 256	–	1,0000	0,0098
3 б		ART-TVS				1,0000	0,0053
3 в		IPMA		500 х 500		0,8366	0,5858
3 г		ART-TVS				1,0000	0,0037
3 д		IPMA	9			1,0000	0,0082
3 е		ART-TVS				1,0000	0,0031
4 а	QR-код	IPMA	7	228 х 228		0,4228	1.0346
4 б		ART-TVS				0,6352	0.8046
4 в		IPMA	17			0,5145	0,9268
4 г		ART-TVS				0,9990	0,0453
4 д		IPMA	34			1,0000	0,0032
4 е		ART-TVS				1,0000	0,0016
5 а		IPMA	31	513 х 513		0,7594	0,6855
5 б			32			0,9994	0,0117
5 в		ART-TVS	20			0,8551	0,5338
5 г			21			0,9989	0,0273
6 а	Шеппа– Логана	IPMA	7	256 х 256	0,1	0,9999	0,0125
6 б		ART-TVS				1,0000	0,0085
6 в	QR-код	IPMA	34	228 х 228		1,0000	0,0044
6 г		ART-TVS	17			0,9975	0,0713
7 а	Шеппа– Логана	IPMA	7	256 х 256	0,5	0,9929	0,1195
7 б		ART-TVS				0,9997	0,0231

а)

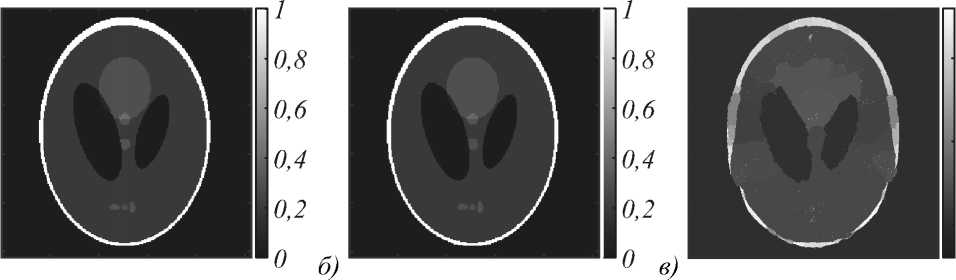
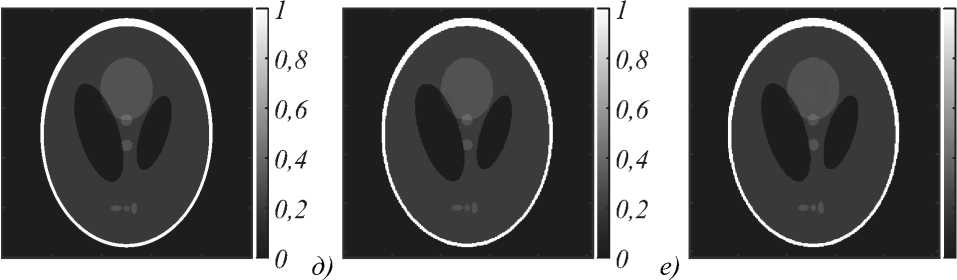
Рис. 3. Реконструкции фантома Шеппа—Логана по идеальным данным: (а) IPMA, 7ракурсов, 256 х 256; (б) ART-TVS, 7 ракурсов, 256 х 256; (в) IPMA, 7ракурсов, 500 х 500; (г) ART-TVS, 7ракурсов, 500 х 500; (д) IPMA, 9ракурсов, 500 х 500;

(е) ART-TVS, 9ракурсов, 500 х 500

Рис. 3 представляет реконструкции фантома Шеп-па–Логана. Начальный выбор числа ракурсов 7 и размера сетки 256 х 256 (рис. 3а и 3б) обусловлен нашим желанием повторить с помощью IPMA и ART-TVS результат, полученный авторами статьи [38]. После нескольких неудачных попыток нам удалось подобрать для IPMA значение параметра регуляризации, близкое к оптимальному (у = 0,01), и получить точ- ную реконструкцию фантома (рис. 3а). ART-TVS также справляется с задачей точной реконструкции фантома Шеппа–Логана по 7 ракурсам (рис. 3б). Причем он делает это и при переходе на более густую сетку 500 х 500 (рис. 3г). А вот IPMA при реконструкции по 7 ракурсам на сетку 500 х 500 имеет проблему со сходимостью к правильному решению (рис. 3в). Мы видим, что мелкие детали фантома на рис. 3в разрешаются неудовлетворительно. Впрочем, стоит только увеличить число ракурсов с 7 до 9, эта проблема исчезает и снова получается неплохой результат (рис. 3д), вполне сравнимый с аналогичной реконструкцией по ART-TVS (рис. 3е). Характеристики качества лучше у нашего алгоритма (табл. 1).

Рис. 4. Реконструкции QR-кода по идеальным данным

на сетку 228 х 228: (а) IPMA, 7ракурсов; (б) ART-TVS,

7 ракурсов; (в) IPMA, 17 ракурсов; (г) ART-TVS, 17 ракурсов; (д) IPMA, 34 ракурса; (е) ART-TVS, 34 ракурса

На рис. 4 представлены реконструкции QR-кода на сетку 228 х 228. Попытки точно восстановить модель по 7 ракурсам с помощью как IPMA (рис. 4а), так и ART-TVS (рис. 4б), очевидно, не увенчались успехом. Точные реконструкции получаются минимум по 17 ракурсам в случае ART-TVS (рис. 4г) и только по 34 ракурсам в случае IPMA (рис.4д). По характеристикам качества (12) и (13) ART-TVS вновь имеет преимущество над IPMA (табл. 1). Что касается результатов восстановления QR-кода на более густую сетку 513 х 513 (рис. 5), то получить точную реконструкцию удается по 21 проекции с помощью ART-TVS (рис. 5г) и по 32 проекциям с помощью IPMA (рис. 5б). Как мы видим, в данном случае увеличивать количество проекций при переходе на более густую сетку потребовалось не для IPMA, а для ART-TVS. В целом анализ результатов, представленных на рис. 3–5, свидетельствует, что для точной реконструкции фантома Шеппа–Логана требуется существенно меньшее количество ракурсов (7–9), нежели для точной реконструкции QR-кода, имеющего высокочастотную структуру (17–34 ракурсов). При этом если в первом случае по данному показателю ART-TVS и IPMA весьма близки друг к другу (7 против 7–9 ракурсов), то во втором ART-TVS заметно превосходит IPMA (17–21 против 32–34 ракурсов). Из полученных результатов также вытекает, что далеко не каждый объект, имеющий кусочно-постоянную структуру, алгоритмы IPMA и ART-TVS способны восстановить точно по числу ракурсов меньше, чем 10. Так, QR-код и, вероятно, другие объекты с высокочастотными составляющими к числу таковых не относятся. В этом смысле необходимы дальнейшие иссле- дования по совершенствованию рассматриваемых, а также других CS-алгоритмов.

0,8

0,6

0,4

0.2

а)

б)

Рис. 5. Реконструкции QR-кода по идеальным данным на сетку 513 х 513: (а) IPMA, 31 ракурс; (б) IPMA, 32 ракурса; (в) ART-TVS, 20 ракурсов; (г) ART-TVS, 21 ракурс

Помимо точности реконструкции, важным критерием сравнения алгоритмов является также время реконструкции. IPMA реализован ресурсоемким методом динамического программирования, а ART-TVS имеет несколько внутренних циклов. Как следствие, время работы обоих алгоритмов измеряется часами даже в 2D-случае. Задачи реконструкции фантома Шеппа–Логана мы запускали на персональных компьютерах с различными характеристиками. Поэтому для данной модели не представляется возможным привести сколько-нибудь корректную статистику по временам реконструкции. На точную реконструкцию QR-кода IPMA затрачивает 3295 с в случае сетки 228 х 228 (рис. 4д) и 31 790 с в случае сетки 513 х 513 (рис. 5б). У ART-TVS соответствующие цифры примерно в 2 раза лучше – 1 743 с (рис. 4г) и 16 978 с (рис. 5г). Это если рассматривать реконструкции по минимальному числу ракурсов, необходимому для точного воспроизведения структур. Если же сравнить времена реконструкции по одинаковому числу ракурсов (34), то здесь ART-TVS имеет десятикратное пре- восходство над IPMA: 320 с (рис.4е) против 3295 с (рис.4д). Все цифры приведены для персонального компьютера Intel PC с процессором 2,6 GHz Core 2 Duo и 4 ГБ RAM. Разумеется, указанные времена счёта могут быть улучшены посредством оптимизации кодов и распараллеливанием вычислений, к чему придётся прибегнуть в обязательном порядке при переходе от реконструкций 2D-изображений к 3D-реконструкциям. Тем не менее представленные выше цифры позволяют судить о том, что и по данному критерию сравнения ART-TVS имеет преимущество над IPMA.

Исследуя алгоритмы реконструкции изображений, естественно задаться вопросом, насколько эти алгоритмы устойчивы к ошибкам результатов измерений, в частности, к шуму проекционных данных. Для ответа на этот вопрос мы наложили на идеальные проекционные данные (11) пуассоновский шум сначала величиной 0,1%. Т.е. к детерминированным величинам (11) мы прибавили возможные значения распределенных по закону Пуассона случайных величин с относительным среднеквадратическим отклонением, равным 0,1% от максимального значения (11). Такая величина шума проекционных данных типична, например, для медицинских применений FVT [22].

Реконструкции моделей, представленные на рис. 6, свидетельствуют: для того чтобы точно восстановить изображение по зашумленным данным, не требуется увеличивать число ракурсов ни в случае IPMA, ни в случае ART-TVS. Это означает, что оба алгоритма вполне устойчивы к шуму заданной величины. Чтобы определиться, какой же из алгоритмов является более устойчивым, мы увеличили значение относительного среднеквадратического отклонения шума до 0,5%. Такой шум следует квалифицировать как аномально большой, т.е. его не должно быть в реальной ситуации. Соответствующие результаты реконструкции фантома Шеппа–Логана приведены на рис. 7. Хорошо видно, что IPMA с таким шумом уже не справляется (рис. 7 а и табл. 1), в то время как с помощью ART-TVS по-прежнему удается получить результат высокого качества (рис. 7 б и табл. 1). Т.е. ART-TVS оказывается более устойчивым к шуму, чем IPMA. Таким образом, по результатам анализа численного эксперимента мы можем с удовлетворением констатировать, что с точки зрения и точности, и скорости реконструкции, и устойчивости к шуму, а также минимального числа ракурсов, необходимого для точной реконструкции, наш алгоритм ART-TVS имеет некоторое преимущество на IPMA.

Заключение

В настоящей статье рассмотрены два алгоритма малоракурсной томографии: итерационный алгоритм минимизации функционала Поттса (IPMA) и алгебраический алгоритм реконструкции с TV-регуляризацией и адаптивной сегментацией (ARTTVS). Мы сравнили их качественно и количественно по таким критериям, как точность и скорость реконструкции, устойчивость к шуму, а также минималь- ное число ракурсов, по которым еще возможно точное воспроизведение структур. Совершенно различные по структуре и содержанию алгоритмы объединяет то, что оба они ориентированы на реконструкцию кусочно-постоянных изображений, используют теорию опознавания со сжатием и совмещают реконструкцию и сегментацию изображений. Для того чтобы выявить лучший из алгоритмов, мы провели численный эксперимент по реконструкции двух 2D-моделей: фантома Шеппа–Логана и QR-кода. Показано, что оба алгоритма способны точно восстановить фантом Шеппа–Логана всего по 7 ракурсам. В случае QR-кода, имеющего высокочастотную структуру, минимальное число ракурсов составляет 17 в случае ART-TVS и 32 – в случае IPMA. Показано также, что ART-TVS превосходит IPMA по количественным характеристикам точности реконструкции, таким как коэффициент корреляции и показатель отклонения, а также выигрывает в скорости реконструкции как минимум в 2 раза. Оба алгоритма устойчивы к шуму проекционных данных, характерному для медицинской компьютерной томографии. Однако лучшую устойчивость к аномально большому шуму проявляет алгоритм ART-TVS. Таким образом, фактически по всем критериям сравнения ART-TVS имеет некоторое преимущество над IPMA.

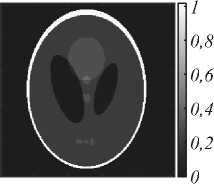
б)

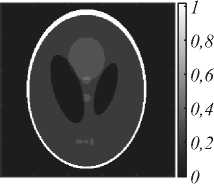
Рис. 6. Реконструкции моделей по данным, зашумленным шумом 0,1% : (а) фантом Шеппа–Логана, IPMA, 7ракурсов, 256 х 256; (б) фантом Шеппа-Логана, ART

TVS, 7ракурсов, 256 х 256; (в) QR-код, IPMA, 34 ракурса, 228 х 228; (г) QR-код, ART-TVS, 17ракурсов, 228 х 228

а)

Рис. 7. Реконструкции фантома Шеппа-Логана по данным, зашумленным шумом 0,5% на сетку 256 х 256: (а) IPMA, 7 ракурсов; (б) ART-TVS, 7 ракурсов

Оба рассмотренных CS-алгоритма успешно используют сегментацию в процессе итерационного восстановления изображения. Можно утверждать, что в случае кусочно-постоянных структур сегментация, реализуемая в алгоритме реконструкции явно (ARTTVS) или неявно (IPMA), дает эффект дополнительной регуляризации, позволяющий улучшить сходимость алгоритма и минимизировать число ракурсов, по которому изображение может быть восстановлено точно. И хотя в случае ART-TVS математически строго данное утверждение еще только предстоит доказать (если это реально возможно), в настоящей статье оно убедительно обосновано представленными практическими примерами.

Хотелось бы сформулировать еще один вывод, который с точки зрения дальнейших перспектив представляется нам, пожалуй, более значимым, нежели полученный ответ на вопрос, какой из двух рассмотренных алгоритмов (IPMA или ART-TVS) лучше. Результаты, приведенные в настоящей статье, показывают, что уже сегодня в мире существуют алгоритмы реконструкции, способные точно восстанавливать внутреннюю структуру объектов по числу ракурсов меньше, чем 10. И пусть сегодня такое утверждение справедливо только для объектов определенного класса, есть все основания полагать, что завтра оно станет реальностью для всех типов объектов без ограничений. Можно также не сомневаться, что количество подобных алгоритмов из года в год будет стремительно увеличиваться. Они будут совершенствоваться и уже в ближайшее время будут в полной мере готовы к практическому использованию как в медицинской, так и немедицинских сферах применения малоракурсной томографии. Таким образом, можно констатировать, что тот качественный переход, о котором было упомянуто во введении (переход от точной реконструкции по 15–20 ракурсам к точной реконструкции по 7–9 ракурсам), очень близок к своему осуществлению.

Не вызывает сомнений, что алгоритм ART-TVS может быть улучшен. Наши дальнейшие исследования будут связаны с разработкой алгоритма адаптивного выбора и подстройки параметров ART-TVS, поиском альтернативного метода сегментации, а также более эффективного стоп-критерия. Успешное решение этих задач должно позволить нашему алгоритму выйти на более высокий качественный уровень и еще в большей степени минимизировать число ракурсов, по которым возможна точная реконструкция. Кроме того, мы планируем ускорить наш алгоритм с помощью GPU или FPGA для того, чтобы сделать практически реальной 3D-реконструкцию. Конечно, особый интерес вызывает адаптация ART-TVS к работе с данными физического эксперимента.