Совместное использование имитационных и аналитических подходов при моделировании эколого-биологических систем

Первые успехи количественной экологии связанны с моделями А. Лотки и В. Вольтерры. Они показали свою эффективность при решении биологически значимых задач, но ограниченные возможности аналитических (докомпьютерных) подходов не позволили развить этот успех. Ситуация изменилась после того, как Дж. Форрестером был предложен метод имитационного моделирования, известный как «системная динамика» с примером его блестящего применения в форме модели современной цивилизации «Мировой динамики (World dynamics)». Метод имитационного моделирования максимально приблизил процедуру построения моделей к экспертам-биологам, сделал их активными участниками на большем числе его этапов: от генерации исходных предположений модели до анализа ее свойств и обсуждений результатов вычислительных экспериментов. Имитационные модели создают возможности для учета практически всех предположений. Это, конечно, приближает модели к реальным объектам, но теряется простота аналитических моделей, может возникнуть эффект «необозримости».

Предлагаемый метод. Для преодоления недостатков имитационных моделей предлагается использовать комплексные исследования. Такие исследования объединяют формальные и неформальные методы, имитационные и аналитические подходы и включают в себя полный набор операций – от отбора биологической информации до построения набора взаимосвязанных моделей, в том числе упрощенных, допускающих аналитические (параметрические) исследования; что позволяет преодолеть недостатки чисто имитационных подходов (ограничения численными расчетами, необозримость моделей, ...). Конечной целью комплексных исследований является формулирование биологически значимых гипотез о механизмах исследуемого явления.

На основе предложенного метода комплексных исследований было проведено моделирование динамики численности популяции леммингов [1, 5]. В частности, было получено следующее разностное уравнение [1, 3, 5]. Для нормированной переменной L = L / L max оно имеет вид

~

L

n + 1

С PL n ,             L n <  1/ P ,

Ln -1/P)  1/P < Ln < B, d,              Ln > B.

где P – прирост биомассы леммингов в благоприятный год; величина 2? определяется из условий возникновения бескормицы в конце зимы; d – нормированная биомасса леммингов в оптимальном биотопе; коэффициент r – характеризует изменение численности леммингов в условиях нехватки кормов в весенний период. График данного уравнения представлен на рис. 1.

Анализ полученного разностного уравнения позволил обосновать гипотезу: ведущее значение в формировании колебаний численности леммингов имеют два безразмерных показателя – относительная скорость прироста численности популяции P и доля выживших особей в наиболее неблагоприятных условиях d (минимальная численность популяции леммингов, после пика). Были проведены вычислительные эксперименты с моделью (1) при сценарии изменения параметра d от 1 до 0 [3]. На рис. 2 представлена зависимость траекторий модели от величины d. Вертикальное сечение графика при выбранном значении d представляет собой точки траектории. Можно видеть, что в этом случае последовательно возникают зоны стабильности с устойчивыми циклами. Внутри зоны стабильности период циклов постоянный, при переходе от одной зоны к другой период изменяется в последовательности натурального ряда (1, 2, 3, 4, …). Зоны стабильности отделены друг от друга переходными зонами с более сложными режимами. Похожая картина наблюдается в исходной имитационной модели [5].

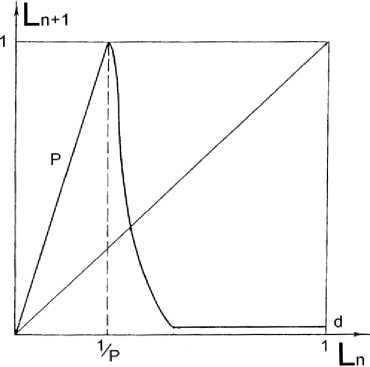
Рис. 1. Функция последования, связывающая численность леммингов L_n в двух соседних годах.

Здесь P – скорость прироста биомассы леммингов в благоприятный год, d – численность леммингов в оптимальном биотопе (после пика численности)

уравнения. В простейшем виде это разностное уравнение можно представить в виде

^Ln + 1

PLn,  L < B, d, L > B.

На рис. 3 представлена зависимость периода цикла от параметров P и d .

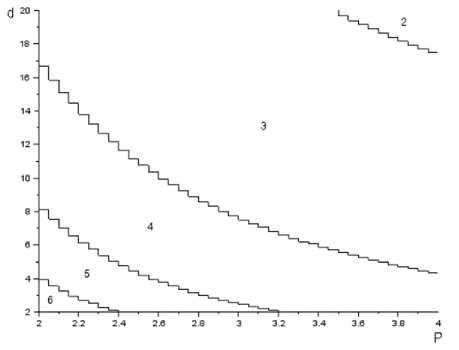
Рис. 3. Зависимость периода цикла от параметров P и d разностного уравнения (2). Цифрами на графике указан период цикла

Параметр Р зависит от многих параметров, в том числе от следующих биологически значимых параметров исходной имитационной модели сообщества «растительность-лемминги-песцы».

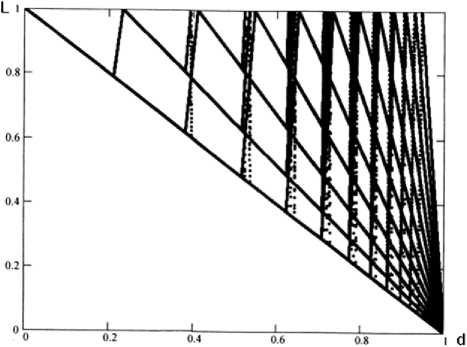
Рис. 2. Зависимость траекторий расчетной модели (1) от параметра d. Результаты вычислительных экспериментов

P = f ( a 2 , b ₅, b ₉, b io ,..)

где a₂ – коэффициент выедания растительности весной и летом, b₅ – коэффициент смертности, если корма хватает, b 9 – коэффициент перехода биомассы растительности в биомассу леммингов для весны и лета, b 10 – коэффициент перехода биомассы растительности в биомассу леммингов для зимы.

На основе анализа разностного уравнения (2), используя формулы пересчета, удалось определить зависимость периода цикла от биологически значимых параметров имитационной модели «растительность–лемминги–песцы» (рис. 4 -7).

Определение длины цикла в зависимости от биологически значимых параметров на основе упрощенной модели. В результате создания набора моделей разной степени детализации и получения формул, связывающих параметры этих моделей, удается произвести приближенное параметрическое исследование исходной имитационной модели с помощью сопряженного разностного

2H----------,----------,---------------------1---------------------,---------------------,---------------------,---------------------1------ ,         ,

0.02       004       0.06       008        0.1        0.12       0 14       0.16

a2

Рис. 4. Зависимость периода цикла от параметра a 2 – скорости выедания растительности леммингами летом

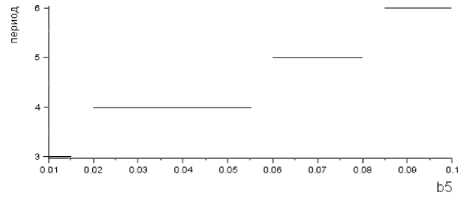
Рис. 5. Зависимость периода цикла от параметра b 5 – коэффициента смертности, если корма достаточно

О 0.1 0.2 0.3 0.4 0.5 0.5 0.7 0.8 0.9    1    1.1 1.2 1.3 1.4 1.5 1.6

Ь9

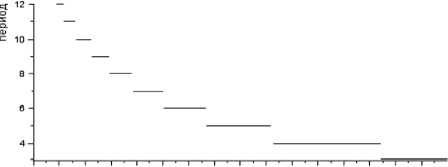
Рис. 6. Зависимость периода цикла от параметра b 9 – коэффициента перехода биомассы растительности в биомассу леммингов для весны и лета

МО

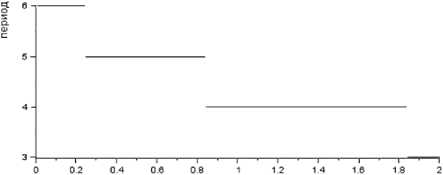
Рис. 7. Зависимость периода цикла от параметра b 10 – коэффициента перехода биомассы растительности в биомассу леммингов для зимы

Выводы: сформулированы количественные гипотезы о ведущих механизмах формирования колебаний численности леммингов. Наличие переходных зон находится в некотором соответствии с зарегистрированной динамикой реальных популяций. При отсутствии четкого трехлетнего цикла, характерного для Таймыра, в более теплых регионах встречаются двух и пятилетние временные интервалы между пиками численности [4]. Полученное разностное уравнение может служить простым инструментарием для прогноза возможной численности леммингов (и, следовательно, песцов), для настройки исходной имитационной модели на необходимые режимы. Для оценки же, например, последствий антропогенных воздействий необходимо использовать детальную имитационную модель. Предложенный метод комплексных исследований может быть использован для изучения других биологических объектов. В частности, он апробирован для исследования взаимодействия северного оленя с кормовыми ресурсами [2].