Совместное распределение огибающих с учетом корреляции

Получен закон распределения огибающих в симметричном виде для узкополосного сигнала в канале с замираниями, когда в точку приема приходит два луча и общий сигнал представляет суперпозицию этих сигналов.

Задачи с математическими моделями, представленными в симметричном виде, зачастую решаются более просто, чем такие же задачи с моделями в несимметричном виде. Типичным примером является распространение понятия спектра на область отрицательных значений. Для описания каналов связи известно [1] совместное распределение плотности вероятности огибающих с учетом их корреляции в нессиметричном виде. Целью данной статьи является получение закона распределения огибающих с учетом их взаимной корреляции в симметричном относительно друг друга виде.

Обычно сигналы, используемые для передачи информации по радиоканалу, являются узкополосными. Узкополосный сигнал s ( t ) описывается изменениями огибающей S ( t ) и фазы 6 ( t ) , изменяющимися значительно медленнее по сравнению с фазой высокочастотного заполнения ω ₀ t при использовании записи вида s ( t ) = S ( t ) cos[ to 0 1 + 9 ( t )] .

При распространении по каналам связи с переменными параметрами сигнал подвергается воз- действию мультипликативной помехи посредством коэффициента передачи k(t): u(t) = k(t)s(t), который изменяет фазу и амплитуду узкополосного сигнала. В каналах с замираниями в точку приема приходит множество лучей, и общий сигнал представляет суперпозицию сигналов ui (t):

n

u(t)=E ui(t) •                 (1)

i =1

Будем считать, что в (1) узкополосные сигналы u i ( t ) можно разложить на квадратурные составляющие (КС) X i и У; , распределенные по нормальному закону:

где K ^-1 – определитель матрицы K ^-1 , обратной корреляционной матрице K = K. . ;

_{M i}                  i,j

^1, j , где K - определитель

;

K j = (-1)"7 K\ корреляционной матрицы K = ||Ki-,j ||; Mi нор определителя |k| , получаемый из него вы-

черкиванием i -ой строки и j -го столбца.

ui (t) = Ai cos(to0t + 0i) = Xi cos(ro0t) - Y sin(^0t)

с математическими ожиданиями m _X и m _Y и дисперсиями ст 2 = ст 2 = ст ² • Коэффициент корреляции между одноименными КС r X i Y i = 0 , а между КС разных сигналов r _X Y, = 0 , r _X ,X, = r _YY, = r i,j •

Плотность распределения вероятности (ПРВ)

n -мерного нормального закона такого закона имеет вид [2]:

wn ^{( Z} 1 , z 2

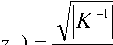
z" ) ( 2п Y

x exp <

I EE k . (Zi

² -= i j= i

— m z ^{)( Z} j — m z Я , ij

i , j - ми-

Считая нечетные номера переменных z в (2) через КС X i , а четные через КС Y i , можно для двух сигналов ( n = 2) с коэффициентом r _{i , j} = r

корреляционную матрицу представить в виде

	⎡1	0	r	0
K=σ 2	⎢⎢ 0	1	0	r
	⎢r	0	1	0
	⎢⎣0	r	0	1

Определитель этой матрицы равен |К| = с ⁸ (1 - r ² ) ² . Обращение матрицы K приводит к матрице вида

		Г 1	0	-r	0
K - 1	⎢ =      1	0	1	0	⎥ -r ⎥
	CT 2 (1 - r 2 )	-r	0	1	0
	⎢	[ 0	-r	0	1 J

определителькоторойравен K ^{- 1}

— 8/1      2\2 • ст (1 - r )

Тогда закон (2) примет вид

W 2 (X 1 , Y 1 , X 2 , Y 2 ) =

____________1____________ ст4 (1 - r2 )(2п)2

	⎧
x exp •	2o- 2 (1 - r 2 )	⎡ 2 2                                           2 2                                   ⎤ EE k i,j ( X i - m X i )( X j - m x j ) + EE 4j( Y i - m Y. )(Yj - m Y , ) ⎣ i= 1 j= 1                                                       i= 1 j= 1                                             ⎦

где k i,j

1, i = j;

⎨

L- r, i * j.

Преобразуем (4) к полярным координатам

Xi = Ai cos 6i ; Yi = Ai sin 0i ;

A,= JX2 + Y2; Si = arctg^L .      (5)

^X i

	dX 1	dX 1	dX 1	dX 1
	dA 1	d θ1	dA 2	d θ2
	dY 1	dY 1	dY 1	dY 1
A -	dA 1	d θ1	dA 2	d θ2
	dX 2	dX 2	dX 2	dX 2
	dA 1	d θ1	dA 2	d θ2
	dY 2	dY 2	dY 2	dY 2
	dA 1	d θ1	dA 2	d θ2

Аналогичным образом для регулярных составляющих амплитуд α и фаз β получим mX, = a cos в ; mYi = a sin в ;

2      2                     ^m Y ²

a = Jm;X, + mY_ ; в = arctg —2^ • mXi

Вычислим якобиан преобразования

который с учетом (5) равняется

	cosθ1	- A 1 sin6 1	0	0
A =	sinθ1 0	A 1 cosθ1 0	0 cosθ2	0 - A 2 sin 0 2	= A i A 2
	0	0	sinθ2	A 2 cosθ2

В полярных координатах ПРВ получается заменой переменных в (4) на новые (5) с учетом якобиана преобразования A = A 1 A 2 :

w2 (A1,91, A2,92) = W2 (X1, Y,, X 2, Y2) A .

Для простоты примем регулярные составляющие фаз β = 0 . Тогда после тригонометрических преобразований получим

w 2 ( A i , 9 1 , A 2 , 9 2 ) =

A 1 A 2

ст ⁴ (1 - r ² )(2 n ) ²

x exp

¥ ( A i , 9 1 , A 2 , 9 2 , a , r ) 1 2ст ² (1 - r ² ) J

x

, (6)

где для удобства при дальнейшем анализе введена функция

T (A1,9 1, A2,92, a, r) = A12 + A22 +

+ 2a (1 - r)[a - A1 cos 9 1 - A2 cos 92 ] - (7) - 2 rA1 A2 cos( 9 1 - 92) .

Для определения совместного распределения огибающих необходимо проинтегрировать (6) по всем переменным в области возможных изменений фаз [ -п , п ] . Если корреляция отсутствует ( r = 0), получим

AA

^W 2 ^{( А} 1 , ⁶ 1 , A 2 , ⁶ 2 ) = ~ 2 4" ^Х

4п ст

Обратное преобразование имеет вид

U1 = (Ai - mi) cos x + (A2 - m2 )sin x,

U2 = (A2 - m2)cosx - (Ai - mi)sinx.

Подставляя в (6) вместо старых координат А ₁ и А ₂ новые U ₁ и U ₂, с учетом (7) получим

V(U1,01 ,U2,02,a,r) = U12 + U22 - - 2r cos(01 - 02 )(U12 - U2 )cos x sin x -- 2UU2r cos(01 - 02 )(cos2 x - sin2 X) + + 2(U 1 cos x - U2 sin x)x x [m1 - a(1 - r)cos 01 - 2rm2 cos(01 - 02)] +

+ 2(U2 cosx + U 1 sin x)x x [m2 - a(1 - r)cos02 - 2rm1 cos(01 - 02)] +

+ ml + m2 - 2a (1 - r) x x (m1 cos 01 + m2 cos02 - 2rm1m2 cos(01 - 02) +

+ 2a ² (1 - r ).

Приравнивая коэффициент при U x U 2 к нулю, получаем решение χ = ± π/4. Для устранения слагаемых с первой степенью огибающих получим систему уравнений

х exp

A + A ² + 2a ²

- 2 A 1 a cos9 1 - 2 A 2 a cos9 ₂ ]

2σ ²

Поскольку здесь переменные A и A ₂ независимы, совместный закон распределения огибающих принимает вид

W ( A i , A 2 ) =

A 1 A 2 σ ⁴

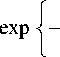
A 2 + A 2 + 2 a ² I —¹------ ²          x

2 ст ²           I

m ₁

⎩ m ₂

- a (1 - r ) cos 0 1 - rm ₂ cos( 0 1 - 0 ₂ ) = 0, - a (1 - r ) cos 0 ₂ - rm 1 cos( 0 1 - 0 ₂ ) = 0,

решение которой имеет вид

M s

= m1 + m2

x

। A 1 a ]| A 2 a

I 0 1 _ 2 I I 0 1 _ 2 <  ст ; <  ст

где I ₀(.) – функция Бесселя первого рода нулевого порядка.

Для интегрирования (5) с учетом корреляции целесообразно произвести разделение переменных интегрирования. В выражении (3) области

интегрирования по квадратурным составляющим представляют собой эллипсы. Поэтому и в поляр-нойсистемекоординатпрификсированныхзначе-нияхХв(6)функция T( A 1 ,0 1 , A 2 ,0 2 , a, r ) = X для огибающих А и А ₂ является эллипсом.

Введем смещение системы координат на величины m и m ₂, соответственно, и повернем ее на угол χ . Новые координаты U и U ₂ связаны со старыми соотношениями

f Ai = (U1 cos x - U2 sin x) + mi,

1                                                (7)

[ A2 = (U2 cos x + U 1 sin x) + m2 ■

M d

m1

= m1 - m.

_ a (1 - r)(cos01 + cos02)

1 - r cos(0 1 - 0 2 )

_ a(1 - r)(cos01 - cos 02)

1 + r cos( 0 1 - 0 2 )

=2(M,.+md)=

x cos0, + rcos02cos(0, -

= a(1 - r )--- ¹—5------——

1 - r2 cos2 (01 - 0 2)

, (9)

, (10)

_{θ 2 )} , (11)

m2 = 2(Ms - Md ) =

²                                     . (12)

x cos02 + rcos0, cos(0, -02)

= a(1 - r )--- ²—5------—---—

1 - r2 cos2 (01 - 0 2)

В результате (6) принимает вид

T (U1,01 ^U 2,02 ,a, r) = U12 [1 - r cos(01 - 02)] +

+ U2 [1 + r cos(0i - 02)] + 2a2 (1 - r) -          (13)

-2[Ms2{1-rcos@ -62)}+Md{1+ rcosfi -0,)}]

и описывает каноническое уравнение эллипса.

Результаты обратного преобразования (8) с учетом (9)-(12) приводят к соотношениям

V2 , .       .

U1 = ~(A1 + A2

4 4

w ( A , a₂ ) = ₄    ²₂ x

O- ⁴ (1 - r ² )

<

U 2

-

--”(A1 - A2

Ms ),- Md),

x exp < -

A 1² + A ₂ ² + 2 a ² (1 -

2 o ² (1 - r ² )

r )

— 1 x

_T ( A, a (1 + r ) К ( A₇ a (1 + r ) 12

^X I 0 I         -2 I I 0 I         -2

(    о ) V    о

при этом функция (13) принимает вид

T(A0, A2,92 ,a, r) =

= A12 + A2 - (A1 + A2 )Ms [1 - r cos(91 - 92)] -

- (A1 - A2 )Md [1 + r cos(91 - 92)]+2a2 (1 - r), и с учетом введенных обозначений (9-(10)

T( Ai ,91, A2,92 ,a, r) =

= A 1² + A 2 - 2 a (1 - r )( A 1 cos 9 2 + A 2 cos 9 1 ) + (14) + 2 a ² (1 - r ).

Такимобразом,совместныйзаконможнопред-ставить в виде произведения двух компонент

W(A,91,A2,92) = W(Ai,92)-W(A2,91), (15)

в котором переменные как по огибающим, так и по фазам разделены, что позволяет получить симметричное выражение для совместных огибающих в виде

Закон распределения (16) имеет симметричный относительно огибающих вид, что отличает его от известных законов [1]. Это позволяет использовать его как для упрощения задач по расчету вероятности ошибки в каналах связи, так и при тестировании программ для исследования систем связи различного назначения с помощью метода статистического имитационного моделирования [3].