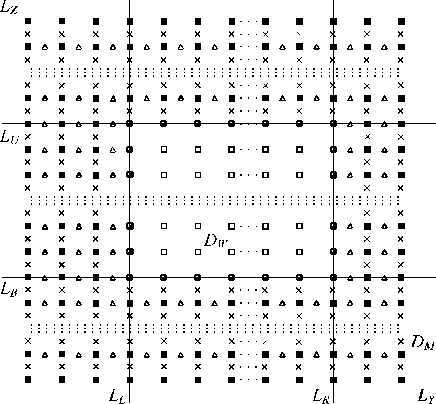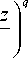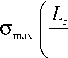Совместное разностное решение уравнений Даламбера и Максвелла. Двумерный случай

Развитие нанофотоники [1] сопровождается как появлением новой элементной базы, так и разработкой численных методов расчёта дифракции света. Наибольшей популярностью среди последних пользуется FDTD (Finite – Difference Time – Domain) подход [2], основанный на разностном решении уравнений Максвелла и характеризующийся в силу этого универсальностью. Он позволяет моделировать распространение произвольных электромагнитных волн в любой среде, в том числе и с учётом их нелинейного взаимодействия. К сожалению, применение упомянутого метода сопровождают высокая вычислительная сложность и требования к объёму оперативной памяти, являясь платой за перечисленные достоинства.

Сокращение вычислительной сложности при реализации FDTD-метода традиционно связывают с использованием аппаратных средств, позволяющих организовывать параллельные и в екторные вычисления по нему. Результаты многолетних исследований в этой области подробно представлены в монографиях [2–4] и использованы при разработке множества программных пакетов, среди которых хочется выделить свободно распространяемые с открыты м кодом MEEP [5] (кластерные вычисления) и B–CALM [6] (вычисления на графических процессорах).

Проблеме сокращ ения объёма оперативной памяти при организации вычислений по рассматриваемому методу также посвящён ряд работ. Например, в [7] и [8] для этого используются подвижные и неравномерные сеточные области, в [9] предлагается декомпозиция области, в [10] – метод пирамид.

Вместе с тем в вычислительной оптике существует тенденция упрощать математическую модель ис-след уемого явления, сводя её к уравнениям, процедура решения которых менее требовательна к системным ресурсам. Например, метод RCWA изначально формулировался для исследования дифракции монохроматического света на решётках, BPM – в скалярном параксиальном приближении и т.д.

Развиваемый в предлагаемой работе подход характеризуется переходом к двумерному случаю ди- фракции TE-волны [2] на цилиндрическом элементе (упрощение модели), приводящему к уравнению Даламбера. Разностное решение последнего (как будет показано далее) совпадает с результатами расчётов по FDTD-методу в указанном случае, но отличается хранением одной сеточной функции на двух временных слоях в отличие от FDTD (три сеточных ф ункции на одном слое по времени), что позволяет на треть сократить требования на объём используемой оперативной памяти. Простота программной реализации также выгодно отличает выбранный подход.

Будучи в свое время в фокусе внимания исследователей, разностное решение уравнения Даламбера постепенно утратило популярность в связи с развитием FDTD-метода и применялось исключительно для формирования поглощающих граничных условий [11] для последнего. Возвращение интереса к нему в настоящее время [12] связано с отмеченными преимуществами, но происходит недостаточно быстро в силу отсутствия разработанного математического аппарата задания падающего поля, наложения поглощающих слоёв и учёта дисперсии материала. Последняя проблема недавно успешно решена в [13], а преодолению двух первых посвящена предлагаемая работа. Авторы находят разумным совместить разностные решения уравнения Даламбера (в области нахождения оптического элемента) и уравнений Максвелла (в поглощающих слоях), сочетая достоинства первого (сокращение требования к объёму оперативной памяти) и второго (разработанный математический аппарат TF/SF-методики и PML-слоёв) методов.

• 1.    Согласование разностных решений уравнений Даламбера и Максвелла на границе сеточных подобластей

Для уравнений Максвелла ограничимся рассмотрением случая Н-волны:

∂Hy   ∂E    ∂H∂

µ0      = - x ,µ0

∂t      ∂z      ∂t∂

∂ E  ∂ H ∂

εε ^x z _-

• 0 ∂t     ∂y∂

  
  

записав разностную схему Yee:

Ц о

н« +0,5 y m , к + 0,5

H n -0,5

y m, к + 0,5

En xm, к+1

Eⁿ x m , к

ht

hz

Задавшись целью совместного отыскания разностного решения уравнений (1) и (3), согласуем вычисления на D^W и D^M в табл. 1.

Ц о

H n +0,5 z m + 0,5, к

H n -0,5 z m + 0,5, к

ht

1 n _En xm+1, к        xm, к hz

E^{n + 1}

^Е 0 ^Е m , к

- En xm, к

H n +0,5 z m + 0,5, к

Hn +0,5

z m - 0 ,5, к

ht

h y

H n + ^0,5 y m , к + 0,5

H n +0,5 y m , к - 0,5

hz

где сеточная проекция электрического поля на ось x -

Eⁿ , магнитного на z и y - H^{n + 0} , ⁵ и H^{n + 0} , ⁵ соответ- x m , к                                                       ^z m+ 0,5, к          ym , к + 0,5

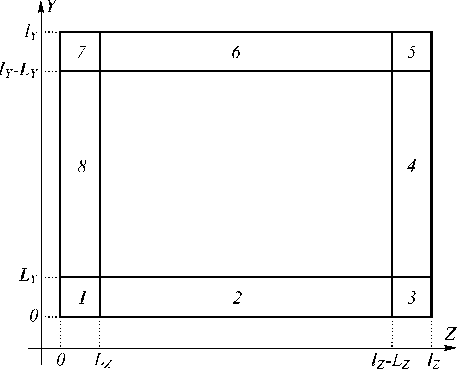
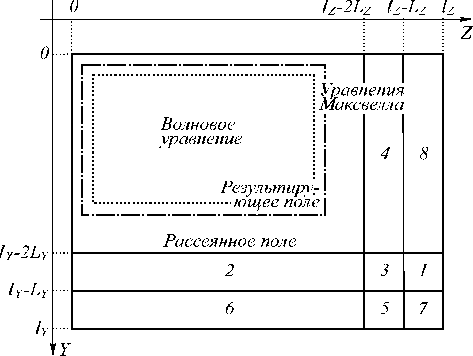
ственно. Решая уравнение (1), введём D (0

N-1, y_m=mh_y, m=1, .., M-1, z_k+0,₅=(k+0,5)h_Z, к=0, .., К-

1}, проекцию    H^n+0,5-    {(tn+0,5,    ym+0,5,    Zk):

zm+ 0,5, к tn+o,5=(n+O,5)ht, n=0, 1, .., N-1, ym+o,5=(m+O,5)hy, m=0, .., M-1, zk=khZ, к=1,.., К-1}. Выделим на D подобласть Dc (0

Таблица 1. Равные значения сеточных функций Exnm,k и Um,,k на границах сеточных областей DM и DW
Границы области	Узлы сеточных областей
W левая граница Dh	m=L, B
W правая граница Dh	m=R, B
W верхняя граница Dh	k=U, L
W нижняя граница Dh	к=В, L

На границах объединённой области установим электрическую стенку. За начальное условие примем отсутствие поля в момент в ремени t=0.

Алгоритм перехода на следующий временной слой при реализации совместного решения состоит в определении сеточных функций в узлах DW и DM в соответствии с табл. 2

Таблица 2. Расчёт совместного решения (1) и (3) на временном слое n+1

считать, что E" определена в узлах{(tn, ym, zk): xm, к tn=nht, n=0, 1, .., N=T/ht, ym=mhy, m=L,...,R, L=Ll/hy,

R=L,/h„ zk=khz, к=В, ..,U, U=Lu/hz, B=Lъ/hz}, Hn+05 -r         z               uz z y                                                                       ?       ym, к+0,5

{(tn+0,5, ym, Zk+0,5): tn+0,5 = (n+0,5)ht, n=0, 1, .., N-1, ym=mhy, m=L+1, .., R-1, Zk+o,5=(k+O,5)hz, к=В, .., U-1}, H"⁺⁰'5 ~ {(tn+0,5, ym+0,5, Zk): tn+0,5 = (n+0,5)ht, n=0, 1, .., N-m+ 0,5, к

1, ym₊₀,₅=(m+0,5)h_y, m=L, .., R-1, z_k=kh_Z, к=В +1, .., К-1}. Тогда решение (1) по схеме (2) будет отыскиваться на DM = D\D^c, а сеточные уравнения схемы (2)

решаться на DM = Dh \Dh.

Аналогично для волнового уравнения:

д U дy 2

+

д²Ux

дz ²

ЦЕ-

д U

д t²

= 0

запишем разностную схему:

иⁿ⁺¹ Um, к

n

^2Um, к

+ U^{n-1 +}Um, к

h2

n c (U m +1, к

^Еm, к

n

^2Um, к

n

⁺Um-1, к

^hy

Um_k+1- 2Uⁿ_mfc + U:_M

I m, к + 1          m, к        m, к 1

hZ

).

Решение (3) будем искать в D^c сеточной области DW, наложенной на D^c, реализуя вычисления по (4) на сеточной области DW . Тогда проекция Um _к определена в узлах {(tn, ym, Zk): t_n=nht, n=0, 1, .., N=T/ht, y_m=mh_y, m=L, .., R, L=Ll/h_y, R=Lr/h_y, z_k=kh_Z, к=В, ..,U, B= Lb/hz, U=Lu/hz}.

Узлы сеточных областей Подобласти вычислительных областей Решаемые уравнения m=0, 0<к<К левая граница DM Enn = 0 xm, к к=0, 0

un+; e 2u:,+une m,k        m,k      m,k	c	n (LVm +1,k	n 2Um,k	+Em-1, k
ht2	Em, k		hy2
u;t+2u:,+u^ m, k + 1         m, k       m, k hz2	^,
un +1e 2u:,+un -п m,k        m,k      m,k	c	n ( Em +1, k	n 2Um,k	+um.	1,k
ht2	Em, k		hy2
unt+i- 2unk + Unmk m, k + 1         m, k       m, k hz2	^,
un +1- 2unfc + une1 m,k        m,k      m,k	c	n (   m+1,k	n 2Um,k	+um.	-1, k
ht2	Em, k		hy2
un,. 1- 2unk+Enk m, k + 1         m, k       m, k hz2	-~),
un +1- 2unmk + un -1 m,k        m,k      m,k	c	n m+1,k	n 2Um,k	+um.	-1, k

+

+

+ ht

t

E m, k hy2

+

чения функци и напряжённости электрического поля (наполовину закрашенные квадратики).

Рис. 1. Объединение сеточных областей без учёта дискретизации по времени.

Квадратам соответствуют проекции Eⁿ, xm,k

+

E

n

' m, k+1

^^^^^^е

ⁿ 2U_m,k

n

⁺Um ,k e1

h

),

z

n+1

Um,k

^^^^^^e

ⁿ 2Um,k

+u

n-1

m,k

c

ht

t

^Em, k

(^U

n

m+1,k

^^^^^^s

ⁿ 2Um,k

+e.

n

m -1,k

h

y

+

Яп +0, 5                           n+0,5

^,, крестикам – H ^, *                                    zm+ 0,5, k                                    ym,k+0,5

+

U

n

m,k+1

^^^^^^s

2U

n

m,k

+E

n

' m, k-1

h

),

z

n+1

Um,k

^^^^^^^

ⁿ 2U_m,k

+U

n -1

m,k

c

ht

t

^Em, k

(^U

n

m+1,k

^^^^^^^

ⁿ 2U_m,k

+E

n

' m-1, k

h

y

+

+

E

n

' m, k+1

^^^^^^^

ⁿ 2Um,k

n

⁺Um ,k e1

h

),

z

n+1

Um,k

^^^^^^^

ⁿ 2Um,k

+U

n-1

m,k

c

ht

t

^Em, k

(

n

Em +1, k

^^^^^^^

2U

n

m,k

h

y

+

E

n

' m, k+1

^^^^^^^

ⁿ 2U_m,k

n

⁺Um ,k e1

h

),

z

+U

n

m -1, k

+

n+1

Um,k

^^^^^^e

ⁿ 2Um,k

+U

П -1

m,k

c

ht

t

Em,k

(

n

Em +1, k

^^^^^^e

2U

n

m,k

h

y

+

U

n

m,k+1

e

2U

n

m,k

+E

n

m ,k e1

h

).

z

+U

n

m -1, k

+

Для подтверждения правомерности предложенного

подхода к совместному решению на одной вычисли-

Эксперименты проводились при различных значениях дискретизации сеточной области Q,Qt и QT, где первый параметр характеризовал число узлов сеточной области по пространств у (приходящееся на одну длину волны); второй – количество узлов по времени (приходящееся на временной интервал, за который плоский волновой фронт в вакууме пройдёт расстояние в одну длину волны); третий – «длительность» запускаемого цуга в длинах волн. При этом они менялись от (10, 20, 5) минимальных значений, удовлетворительно описывающих распространение плоской однородной волны в свободном пространстве, до (100, 200, 15), соответствующих весьма низким величинам погрешности. В качестве вычислительной области D брался квадрат с длиной стороны 20λ, при этом шаги по пространств у полагались равными.

В первой серии экспериментов были повторены результаты из работы [14], полученные при распространении плоской однородной электромагнитной волны в вакууме при задании жёсткого источника. Их совпадение свидетельствует о правомерности излагаемого выше подхода в случае свободного пространства.

тельной области уравнений Максвелла и волнового

уравнения авторы провели серии вычислительных экспериментов. При этом использовались операционная система Windows 7 Professional SP1, вычислительный комплекс Matlab 7.0.1 и процессор Pentium (R) Dual – Core CPU T 4400 @ 2.20 GHz, RAM 3.00 CB.

На рис.1 уравнения Максвелла решаются относительно сеточных функций Hz (обозначены треугольниками), Hy (крестиками) и Ex (закрашенными квадратиками); уравнения Даламбера – относительно сеточных функций Ex (незакрашенными квадратиками); на общей границе сеточных областей расположены зна-

2. Задание падающей волны по технологии TF/SF при совместном решении

Моделирование распространения излучения через оптический элемент, кроме наложения сеточной области и записи на ней разностных уравнений, т реб ует задания приходящего извне поля, падающего на элемент. Действительно, результат б удет зависеть не только от геометрии изучаемого оптического элемента и материала, из которого он изготовлен, но и от вида падающей электромагнитной волны – распределения комплексных амплитуд проекций её векторов в пространстве и времени .

Непосредственное использование модели жёсткого источника (вполне приемлемой в одномерном случае) в двумерном варианте оказывается неудачным при необходимости корректной работы с отражённой от оптического элемента волны. Наиболее популярным приёмом в этом случае является задани е падающей волны по технологии TF/SF, связанной с искусственным разделением поля на результирующее (в оптическом элементе и его непосредственной окрестности) и рассеянное (в остальной области). Выражения, описывающие указанное разделение полей, содержат слагаемы е с аналитически (или численно) заданным падающим полем. Таким образом, происходит учёт последнего.

Реализация методики TF/SF связана со след ующей модификацией разностной схемы Yee:

г

En+1

xLs1,k

E^{n x}Ls, k

Hn^+0,5 zLs0 ,5,k

(H

n+0,5

^zL-1,5, k

+ H

. n+0,5

zL-1,5, k

)

г

ht

hy

Ц

~ n+0,5   ~ns0,5

H yk+0,5 ^sH yk+0,5 h_t

^Exk+1   ^Exk

hz

k = 0, K s 1, n = 0, N s 1,

г

_Fn + 1

Ex_k

Ex_k

ht

~ n+0,5   ~ n+0,5

Hyk+0,5 ^sHyks0,5

hz

k = 0, K, k = 0, N s 1,

Eb s1 = sin tonht.

Hn+0,5 yLs1,k+0,5

En+1 xR+1,

H n+0,5 yLs1,ks0,5

hz

;

1,k

Eⁿ xR+1,k

( Hn+0,5 zR+1,5,k

+ H

, n+0,5

^yR+1,5, k

) _sHⁿ⁺0,5 zR+0,5,k

H

г

ht

hy

n+0,5

yR+1,k+0,5

En⁺¹

xm,U+1

Hn^+0,5 yR+1,ks0,5

hz

E

n

xm, U+1

г

;

H n+0,5 zm+0,5,

, U+1

H n+0,5 zms0,5,U+1

ht

hy

Замысел второй серии экспериментов состоял в верификации возможности задания падающей волны по методике TF/SF при совместном решении уравнений Максвелла и Даламбера.

Усложняя задачу (по сравнению с первой серией экспериментов), исслед уем дифракцию на бесконечном однородном диэлектрическом цилиндре кругового сечения, совместив его центр с центром области D^c , определив радиус, равный половине длины волны, показатель преломления n=1,5. Остальные параметры вычислительного эксперимента остались аналогичными первой серии. Сравнивая полученные результаты с известным аналитическим решением [15], для оценки погрешности воспользуемся величиной εR

A_k sN\

(г_д= max^J-------¹, N - значения, полученные разно -

R k      Ak стными методами, Ak – соответствующие аналитическому решению), отыскивая её на оптической оси элемента, варьируя k = B,U и m = 10Q + 1.

(Hn+0,5

ym,U+1,5

En+1

xm,Bs1

s

s

+ H

n+0,5

ym, U+1,5

) s H

n+0,5

ym,U+0,5

hz

;

Eⁿ xm,Bs1

H n+0,5 zm+0,5,Bs1

s

H n+0,5 zms0,5,Bs1

s

ht

hy

Hn+0,5 ym ,Bs0,5

s

(H

n+0,5

ym,Bs0,5

+H

. n+0,5

ym, B 4,5

)

H

n+0,5

hz

;

Таблица 3. Результаты второй серии вычислительных экспериментов

Число шагов		QT = 5	QT = 10	QT = 15
Q	Qt	£r
10	20	0,1338	0,1424	0,0809
20	40	0,0608	0,0682	0,0183
50	100	0,0307	0,0215	0,0075
100	200	0,0274	0,0096	0,0037

Ц

zLs1,5,k

s

Hn s0,5 zLs1,5,k

(En xLs1, k

s

n

^ExL s1,k

) sEn xLs2, k

ht

hy

;

Ц

Hn+0,5 zR+1,5,k

s

Hns 0,5 zR+1,5,k

Eⁿ xR+2,k

s

(Eⁿ

^{V   x}R+1, k

s

n

Ex xR+1,k

)

ht

hy

;

Ц

Hn+0,5 ym,Bs1,5

s

Hns0,5 ym, B s1,5

s

(En xm,Bs1

s

F ⁿ

E xm,Bs1

) s Eⁿ

^       xm, B s2

ht

hz

;

Ц

Hn+0,5 ym ,U+1,5

s

Hns 0,5 ym,U+1,5

s

Eⁿ xm,U+2

s

(Eⁿ

^X xm Ц+1

s

n

Ex xm,U+1

)

ht

hz

,

где сеточные функции под тильдо й свя заны с падающим по лем и являются его компонентами. Ав-

торы остановились на численном зад ании пад аю-щего поля, для чего отыскивают разностное решение одномерных уравнений Максвелла с привлечением жёсткого источника:

Рассматрив ая результаты из табл. 3, соответствующие как совместному решению уравнений Даламбера и Максвелла, так и разностному решению исключительно уравнений Максвелла, отметим точное совпадение обоих решений при любых параметрах дискретизации и сходимость разностного решения к аналитическому.

Очевидно, для получения удовлетворительного результата (сочтём за него решение не более чем с 2% погрешностью) достаточно использовать цуг в 10 длин волн. При QT = 15 удовлетворительный результат достигается при дискретизации Q,Qt, равной (20, 40). При меньшей длине цуга поле в исслед уемой области не успевает устояться, волна не является монохроматической, в силу чего результаты характеризуются высокой погрешностью. Таким образом, можно заключить, что разработанный метод является достойной альтернативой «чистому» FDTD.

3. Наложение поглощающего слоя при совместном решении

Важной задачей при моделировании дифракции электромагнитного излучения разностным методом является помещение поглощающих слоёв (PML – perfectly matched layer [16]) у границ вычислительной области для исключения отражения от последних. По замыслу авторов настоящей работы, рассмотрение задачи дифракции на оптическом элементе уместно связывать с решением волнового уравнения в области непосредственного нахождения этого элемента, а организацию поглощения у границ вычислительной области (вне элемента) – с решением уравнений Максвелла, моделирующим PML-слой. При этом сокращаются требования к системным ресурсам ЭВМ по сравнению с FDTD-методом (в двумерном случае) и используется современная методика наложения PML-слоя вместо устаревшего подхода Мура [11], традиционно сопровождающего решение волнового уравнения.

Один из способов записи уравнений Максвелла в поглощающем слое (предложен Беренже в 1994 году [16]) характеризуется введением, наряду с электрической проводимостью σ, магнитной σ*, связанных соотношением σ = (ε₀ /µ₀)σ^*. Тогда уравнения (1) при-

σz

-

L z

в областях 1, 8, 7;

σ max

Lz

σz

- lz + z

L z в областях 3, 4, 5, где q ∈ R .

Рис. 2. Схема расположения PML

нимают вид:

∂H

µ ∂ty+σ∗Hy= µ∂Hz +σ∗Hz = ∂t

-

-

∂Ex ∂z ;

∂Ex ∂y ;

∂E       ∂H

ε x + σE = z

∂t

x    _∂y

-

∂Hy ∂z

.

Представляя распространение

и затухание поля

вдоль разных направлений отдельными уравнениями, производят расщепление электрической компоненты и проводимостей [16], записывая

µ∂∂Hty +σ∗zHy= µ∂∂Htz+σ∗yHz=

-

∂(E -E ) xz xy

∂z ∂(Exz+Exy)

Соответствующая конечно-разностная аппроксимация (16) в поглощающих слоях [16]:

Hn+0,5 _-Hn-0,5 0    ym,k+0,5          ym ,k+0,5

ht

+σ^∗H zm ,k+0,5

n-0,5

ym ,k+0,5

En -En  +En xym,k+1        xym,k         xzm,k+1

hz

Hn+0,5 - H n-0,5 zm+0,5,k          zm+0,5,k ht

+σ

-

Eⁿ xzm ,k

∗ ym+0,5,k

H n-0,5 zm+0,5,k

n nn n

Exym+1,k    Exym ,k⁺Exzm+1,k    Exzm, k

hz

εm,k

En+1 xzm,k

-

Eⁿ xzm,k

ht

+σ zm,k

Eⁿ xzm,k

hz

ε ∂Exz + σ E

_∂t       z xz

∂E_xy

ε ∂t + σyExy

∂y      ;

_-∂Hy;

∂z

∂Hz

∂y ,

где Ex = Exz + Exy , а отличные от нуля проекции µ0σy = ε0 σ^∗_y и µ0σz = ε0 σ^∗_z обеспечат затухание волны в соответствующих направлениях.

Располагая поглощающие слои, как показано на рис. 2, определяют отличные от нуля проводимости в виде:

σy⁼ σmax

( Ly - y

L к y 7

к^

, в областях 1, 2, 3;

εm,k

n+1 xy_m,k

En xym,k

ht

+σ Eⁿ ym ,k xym,k

Hn+0,5 zm+0 ,5,k

_-H n+0,5 zm-0,5,k

.

hy

σy⁼ σmax

Г L

y

-

l_y + y

q

L

к у 7

, в областях 5, 6, 7;

Упрощая программную реализацию вычислений по схеме (17) и оптимизируя её векторизацию (увеличивая длину векторов в PML-области [17]), авторы переходят от краевых условий первого рода (электрической стенки) к периодическим условиям [18], что позволяет объединить поглощающие слои. В частности, прежние слои с нечётными номерами объединятся в один, также попарно объединятся слои 2, 6 и 4, 8 (рис. 3).

Таким образом, на рис. 3 б удем различать границы вычислительной области (чёрная линия), поглощающих слоёв (тонкая чёрная линия), рассеянного и результирующего полей (пунктирная линия) и сеточных областей D_h^Mи D_h^W (линия из точек).

В ходе третьей серии вычислительных экспериментов определим толщину объединённых поглощающих слоёв в две длины волны, длину квадратной

вычислительной области (Ly=Lz) положим равной четырём длинам волн (сократив по сравнению с предыдущими экспериментами на порядок за счёт использования PML).

Рис. 3. Взаимное расположение TF/SF, PML и области решения волнового уравнения при циклических граничных условиях

Параметры поглощающих слоёв σmax и q б удем варьировать в зависимости от дискретизации сеточной области, след уя рекомендациям из [19]. Границу раздела полей расположим непосредственно за граничными условиями (левая и верхняя части границы раздела) и PML-слоями (нижняя и правая части) на расстоянии одного шага сеточной области по пространству от них. На таком же расстоянии от границы полей расположим границу раздела сеточных областей. Центр диэлектрического цилиндра разместим в точке (λ, λ).

Разница межд у разностным решением уравнений Максвелла на всей вычислительной области (классический подход) и совместным решением уравнений Максвелла и Даламбера (авторский метод) является незначительной (порядка машинного нуля) при всех параметрах дискретизации.

Таблица 4. Результаты третьей серии вычислительных экспериментов

Число шагов		QT =10	QT = 15
Q	Qt	εR
10	20	0,1629	0,1576
20	40	0,0628	0,0592
50	100	0,0206	0,0221
100	200	0,0087	0,0088

Отметим, что в отличие от предыдущего случая (табл. 3) увеличение длительности временного интервала с QT=10 до QT=15 не привело к заметному снижению погрешности (табл. 4). Если при QT=10 результаты из табл. 3 и 4 почти совпадают (применение PML не внесло значимых искажений в результат), то для QT=15 они отличаются в два–три раза. Следовательно, величины из последней колонки табл. 4 характеризуют в значительной степени погрешность, связанную с использованием PML-слоёв.

Заключение

В настоящей работе продемонстрирована возможность совместного разностного решения уравнений Даламбера и Максвелла, при котором на область вычислительного эксперимента налагаются различные сеточные подобласти. Указанное разностное решение обеспечивается согласованием значений сеточных функц ий на границе таких подобластей.

На примере задачи дифракции плоской волны на цилиндре было проведено исследование сходимости численного решения к аналитическому при уменьшении шагов дискретизации, которое выявило снижение погрешности примерно в два раза при одновременном уменьшении шагов.

При совместном численном решении была использована методика TF/SF, применение которой при использовании только волнового уравнения является малоэффективной, а также наложение поглощающих слоёв (PML). Результаты использования обеих методик при совместном решении уравнений Максвелла и волнового уравнения практически неотличимы от аналогичного решения уравнений Максвелла, что позволяет говорить об эквивалентности сеточных задач и, соответственно, получаемы х реш ениях.

Таким образом, совестное решение разностных уравнений Максвелла и Даламбера позволяет использовать лучшие стороны обоих методов.