Совместное решение уравнения Клейна–Гордона и системы уравнений Максвелла

Изучение взаимодействия электромагнитного поля с веществом – важнейшая и старейшая тема как классической, так и квантовой физики. Она имеет множество ответвлений, одним из которых является взаимодействие сильного импульсного лазерного поля с атомами и молекулами. Под «сильным» здесь понимается поле, сравнимое с электрическим полем в атоме, удерживающим электроны вокруг ядра. Сильное поле может приводить к интенсивной одно- и многократной ионизации атома или молекулы. Изучая угловые и энергетические распределения этих электронов, физики рассчитывают получить информацию о структуре квантового объекта и тонких механизмах ионизации (отрыва электрона от атома). Становление теории таких процессов связывают с пионерскими работами Л.В. Келдыша [1] и его последователей. С тех пор появилось множество работ, где анализировались плюсы и минусы этой теории, исследовались границы применимости. Одно поверхностное их перечисление заняло бы половину объёма журнала, поэтому мы отметим только несколько недавних обзоров [2-12], где можно видеть пути развития данной науки. Теоретическое и математическое содержание большинства работ последних лет, однако, сместилось в сторону развития численных схем решения базовых уравнений, что связано с интенсивным ростом вычислительных возможностей современных ЭВМ. Несмотря на значительный прогресс такого подхода в понимании процессов, происходящих в квантовом объекте под действием интенсивного электрического лазерного импульса, аналитические модели остаются чрезвычайно актуальными, поскольку имеют предсказательное значение. Точное решение поставленной задачи известно для очень небольшого круга локальных потенциалов, в частности для потенциала осциллятора [4, 5]. Однако в этом поле нет состояний ионизации. Для простейшего акту- ального случая атома водорода уже приходится рассматривать различные приближения, математическая корректность которых не всегда ясна. В этой связи на помощь часто приходит свойство калибровочной инвариантности электромагнитного поля, которое, в свою очередь, позволяет получать различные эквивалентные формы уравнения Шрёдингера, связанные между собой унитарными преобразованиями, которые, как известно, ведут к инвариантности физических величин, задаваемых квадратичными формами волновой функции. Напомним, что уравнения Максвелла для электромагнитного поля можно записать в терминах скалярного и векторного потенциалов. Эти потенциалы вполне однозначно определяют наблюдаемые характеристики электромагнитного поля: напряжённости электрического и магнитного полей. При этом сами потенциалы определены неоднозначно. Например, два набора потенциалов дают одни и те же напряжённости электрического и магнитного полей для произвольной функции.

Формы уравнения Шрёдингера при использовании различных калибровочных преобразований электромагнитного поля и некоторые полезные следствия составляют содержание данной работы.

Строгое описание взаимодействия электромагнитного поля с носителями заряда, находящимися в периодическом поле кристаллической решётки, возможно только в рамках квантовой теории поля. Описание кинетических явлений в твёрдых телах, основанное на квантово-полевой теории, приводит к сложным уравнениям, анализ которых затруднён. Однако во многих практически важных случаях для описания явлений можно применить подход, основанный на решении одночастичных уравнений.

Трудность состоит в том, что обычно поведение носителей заряда в кристалле описывается с помощью уравнения Шрёдингера, которое не является инвариантным относительно преобразований Лоренца, а поведение электромагнитного поля описы- вается с помощью уравнений Максвелла, которые обладают релятивистской инвариантностью. Это приводит к тому, что трудно построить законченную теорию, которая описывает поведение носителей заряда в кристалле при наличии электромагнитного поля. Выход состоит в использовании уравнения Клейна–Гордона для описания поведения носителей заряда. В результате получаются правильные выражения для плотности тока и заряда, которые, в свою очередь, удовлетворяют закону сохранения электрического заряда. Следует отметить, что заряды и токи, входящие в уравнения Максвелла, должны удовлетворять этим требованиям.

Недостаток существующих записей уравнений, которые включают систему уравнений Максвелла и уравнение Шрёдингера (Клейна–Гордона), состоит в том, что уравнения Максвелла записаны относительно электромагнитных полей, а уравнение Шрёдингера или Клейна–Гордона в стандартной записи содержат электромагнитные потенциалы.

Другая сложность состоит в том, что полученная система уравнений не обладает свойством линейности. Это связано с тем, что выражения для плотности токов и зарядов содержат произведения волновой функции и её комплексного сопряжения.

Современное состояние проблемы изложено в работах [13, 14]. Однако в этих публикациях не приведены явные выражения для решений уравнения Клейна– Гордона в присутствии электромагнитного поля.

В данной работе предлагается запись системы уравнений, описывающей взаимодействие квантовой системы с электромагнитным полем, без указанных выше недостатков.

Рассмотрено калибровочное преобразование, приводящее к тому, что уравнение Клейна–Гордона также содержит выражения для электромагнитных полей.

Система уравнений, полученная в данной работе, линеаризуется. Линеаризация возможна в случае, когда внешнее электромагнитное поле является слабым по сравнению с кристаллическим полем. Для решения линеаризованных уравнений можно использовать методы, которые используются для решения уравнений Максвелла, например метод разделения переменных или метод разложения по базису.

• 1.    Основные положения

  • 1.1.    Уравнения Максвелла в присутствии заряженного скалярного поля

Поведение заряженной частицы в электромагнитном поле описывается системой уравнения Максвелла и уравнения Клейна–Гордона.

Система уравнений Максвелла имеет вид

4nj  1 дЕ rot H =+, c c д t (1) 1 дН rot E =, c д t (2) div H = 0, (3) div E = 4 пр ,

где E , H - напряжённости электрического и магнитного полей, j , р - плотности токов и зарядов [15, 16]:

р =

e

2 mc ²

|     д v| ih— + e ф№* l д tI

д aLiI

V I ih--eф I v , l дtI

• e i f f w e * I

• 1    =-- I v - ih V + — A v - 2 mV I I c J

, , ll                        J

I

e

• -| v I - ih V — A IV I I , ll c ) J)

A , ф - электромагнитные потенциалы, v - волновая функция заряженной частицы.

Уравнение Клейна–Гордона для волновой функции имеет вид [15, 16]

—г I ih--eф I v = c2I    д t       I

e I 2 2

- ih V — A I v + m c v . c )

Плотность заряда и плотность тока нельзя выбирать произвольно. Они должны быть связаны законом сохранения заряда ip+div j=0.                                (8)

Уравнения (1 – 8) полностью описывают движение заряженной частицы в электромагнитном поле. При этом частица описывается с помощью одночастичного квантово-механического уравнения, а электромагнитное поле – с помощью неквантовых уравнений Максвелла.

Электромагнитные потенциалы связаны с электромагнитными полями следующими соотношениями

1 ал

E = - - -Vф ,                          (9)

c д t

H = rot A .

Условие калибровки следует из закона сохранения заряда и имеет следующий вид:

• - дф ( x , t )

д—- + div A ( x , t ) = 0.                   (11)

В отличие от электрического и магнитного полей электромагнитные потенциалы определены неоднозначно. Нетрудно показать, что выражения для напряжённостей электрического и магнитного полей и условие калибровки потенциалов остаются неизменными, если сделать преобразование вида ф = ф- + - ^X ,                               (12)

c д t

A = A , -Vx ,                             (13)

если функция x удовлетворяет уравнению

A dx c ² d t²

-V ² / — 0.

Данное преобразование называется калибровочным. С помощью калибровочного преобразования можно добиться, что потенциал электрического поля будет равен нулю. В этом случае электромагнитное поле будет описываться только одним векторным потенциалом. Пусть функция х имеет вид

Система уравнений (7)-(10), записанная в таком виде, затрудняет описание взаимодействия квантовой заряженной частицы с электромагнитным полем. Это связано с тем, что в уравнение Клейна– Гордона входят не сами поля, а электромагнитные потенциалы.

1.2. Представление электромагнитных потенциалов в виде суперпозиции плоских волн

t

х(x, t) — c J ф(x,т)dт .                            (15)

-да

Тогда

Внешнее электромагнитное поле создаётся зарядами и токами. В этом случае уравнения для потенциалов будут неоднородными линейными дифференциальными уравнениями. Однако во многих практически значимых случаях функции, описы-

ф ( x , t ) = Ф 1 ( x , t )

d

+ — d t

' t                     Y

Jф( x,т) dT

(-да                 ,

вающие электромагнитные потенциалы, соответст-

вующие внешним электромагнитным полям, удов-

t

A ( x , t ) = A , ( x , t ) - c J Vф ( x , т ) d T .              (17)

-да

летворяют однородным волновым уравнениям. Примером таких полей могут служить гауссовы и бесселевы пучки, рассмотренные в работах [17-20].

В этом случае векторный и скалярный потенциал

Подставляя в уравнение калибровки (11) выражения новых потенциалов через старые, получаем:

можно представить в виде суперпозиции плоских

волн:

'

1 ^f c d t

Ф 1 ( x , t )

d

+ — d t

' t                     Y

Jф( x,т) dт

(-да               )

ф “ 1 “ 2 “

+

П —

+div A ( x, t )-c JVф( x, т) dT = 0,

A ¹

A ²

( A ³ V

-да

1 5Ф 1 ( x , t )

c

dt

+ div A 1 ( x , t ) +

+c

1 d ²

c ² d t ²

' t

J ф ( x , т ) d т

(-да

Y

V

Ш А ^{1 а} 1 «_2Ю

A 2 a_]a, 2 to

A 3 a 1 a 2 ®

I ® I x exp i—I 2 , ajxJ -( c (j—1

ct I I da1da2d®,

где

a2 — 1 - a1 - a2 .

' t-

- div I J Vф ( x , т ) d т

( -да

= 0.

Калибровочное условие в этом случае приобретает вид

Потенциал удовлетворяет однородному

волно-

_ф ^{a ] a} 2 ™₊^ 2 a _jA ^{j a ] a 2 m} — 0. j — 1

вому уравнению, и тогда остаётся доказать, что

'

t

Y

t

Д 2 t                        t

Jф(x,т)dт — J d t

д ² ф ( x , т )

(-да

V

-да

d t ²

d т ,

дф ( x , т ) дф ( x , t ) дф ( x , да ) ------ —---

dt

dt

dt

.

Последнее равенство выполнимо при условии, что потенциал ф удовлетворяет соотношениям:

дф ^x,да)

ф ( x ,да ) — 0, ^{v (}    ) — 0.

^{v 7} д t

В случае, когда новый электрический потенциал ф1 — 0, калибровочное уравнение будет иметь простой вид div A1 — 0.                                  (22)

Это означает, что поле в свободном пространстве поперечно. Данное преобразование можно выполнить только в области, где отсутствуют свободные заряды и токи.

Разложение (23) можно также записать в виде n— JJJ ( B -'^a- e 0a„ + B ¹"'- 4a,. +

+ B 2 a 1	a 2 e9 2^0		+ B 3a1a 2	2 e	3 a, 1 a2	)x				(26)
	'	^'	3		V
x exp	i		E a j x	—	ct I	d a 1		d a 2	d ® .
	(	c (	j — 1		VV
Базисные вектора имеют следующий вид:
		' 1 Y			' 0	Y
		0			-a	2
e 0 a,1 a2	—	0	, e .,	—	a 1		’
		( 0 V			( 0	V
		'	0 Y					' 0		(27)
			a 1
								a 1
e 2 a.1 a2	—	a 2 22 a 1 + a 9		'	e 3 a.1 a2		—	a 2
		(	a 3 V					( a 3

Коэффициенты в разложении (23) можно найти, если известны соответствующие коэффициенты в

Обращая (33), получим следующее выражение для коэффициентов B^{j a 1} “ ² :

разложении электрического и магнитного поля, которые, в свою очередь, можно найти, если известно распределение электрического поля в некоторой плоскости. Получив выражения для потенциалов, можно решить уравнение Клейна–Гордона в присутствии электромагнитных полей.

Выразим коэффициенты разложения для элек-

Г g ( ™ ) m ^{a 1 a} 2 ™

B ^a1^a2      -    / ------

X ²

I-1

JJJ ^{E ( x 12 x 2},0, t ^)x

Г ™           A x exp I — i—Xajxj + iot I dx^dx2dt.

V ^c j = 1               V

тромагнитных потенциалов через значение электрического поля в некоторой плоскости. Учитывая разложение четырёхмерного потенциала электромагнитного поля по плоским волнам (23) и выражение электрического поля через потенциалы (9), получим

Таким образом, если известно распределение электрического поля в плоскости z = 0 , то можно найти распределение электромагнитных потенциалов в пространстве (в том числе области нахождения квантового объекта).

следующую связь:

' A l»^a'^o>

E ( x , t )

= Ш A ² “ 1 “ 2 ™ —¹

а ₁ ф “ ¹ “ 2 ™

A

■ а₂ ф “ ¹ “ ² ™

X

A 3 0.1 ^ 2^,

—।

■ a₃ ф “ ¹ “ ² ™

V

1.3. Уравнения Клейна–Гордона в электромагнитном поле

В данном разделе рассмотрим более подробно уравнение Клейна–Гордона. В символическом виде это уравнение для свободной частицы имеет вид [15, 16]:

v

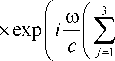
a jx^j

—

ct I I d a ₁d a ₂d o .

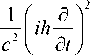
2  .22

V = p V + m c V ,

Учитывая условие калибровки (25), получаем

где p = — ih V , m - масса частицы, c - скорость све

выражение для электрического поля в виде

Г                       A

A1"1"2™ — a1 XajAj j=1

та, h - постоянная Планка, V — волновая функция

E (V ) = JJJ

A 2 a. 1 a. 2 to

— a ₂ X a _jA ^j “ 1 “ 2 “ j = 1

X

A Sa^a^o

V

«3 X" A j=1               V

О I

^X exp ' -| X V ^c j

V

a jx^j

ct

d a ₁d a ₂d o .

V

частицы.

Отметим, что символическая запись представляет собой выражение, которое связывает энергию релятивистской частицы с её импульсом.

Чтобы получить уравнения Клейна–Гордона для частицы в электромагнитном поле, сделаем стандартную [15, 16] замену операторов е      5      5

— ih V ^ — ih V — A , ih--> ih--e ф ,       (36)

c       dt      d t где A - векторный потенциал поля, ф - электриче-

Полученное выражение можно переписать в виде E ( x , t ) = JJJ M ""2 ™ A ^a " 2 ™ x

ский потенциал поля, e – заряд частицы. Тогда выражение (35) преобразуется:

Г.™j x exp I i — X"xj — ' ™ t I da1 da2 do.

V c^ V

1 L5 J г V 'h 57"eТ =

• 7 n e л I           2 2

— ih V — A I v + m c V . c V

Далее рассмотрим случай, когда функции коэффициентов представляются в виде

A ^{j a} 1 “ 2 ™ = g ( ™ ) B ■" ,

Раскрывая скобки и учитывая некоммутатив-ность операторов, входящих в (37), получаем:

1 Г /2 d2V ., дф dv , / xV ^A

• — h ——- ihe v --2 'he ф— + ( e ф ) V =

• c ² V       д t ²            д t            д t ^v V

тогда

E ( x , t ) = JJJ g ( o ) M ^{a 1} “ 2 ™ B ^{a 1} “ 2 x

C™j x exp I i —X"xj — i ™ t I da1 da2 do.

V c^ V

= — h ²V ² v + ih- ( V A ) v + 2 ihe A ( Vv ) +      (38)

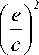
A 2 v + m ² c 2 V .

Для того, чтобы найти коэффициенты B^j " " 2 , рассмотрим выражение для электрического поля в плоскости z = 0 .

Члены — ihe v ( 1/ c ² ) -дф / д t и ih ( e / c )( V A ) v со-

кращаются в соответствии с калибровочным соотношением (17), тогда

E ( x ¹, x ²,0, t ) = JJJ g ( o ) M ^{a 1} “ 2 ™ B ^{a 1} “ 2 x

Г.™j L x exp I i —X«jxj — i ™ t I da1 da2 do.

V c jt V

1 I 2 д2v       ,дv)

— — h —— — 2 ihe ф— = c2 V     дt2           дt)

2                        (39)

= — h ²V2v + 2 ihe A ( Vv ) + | e | ( A ² — ф² ) v + m ² c ²V. c V c J ^v ’

Для широкого спектра задач квантовой механики можно использовать нерелятивистское приближение. Представим волновую функцию в виде

v ( x , y , z , t ) = exp

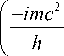
t lx ( x , У , z , t ) .

В результате получаем окончательное выражение для уравнения (39):

(. e ф |dx hh .

ih\ 1-- 2 , V X + e Фx +

V mc J dt    2m e              1 fe

+ ih —A ( Vx ) + — |-l ( A -ф ) x +        (41)

mc        2 m V c J

₊ h ² d^x

2 mc ² d t ²

Рассмотрим калибровочное свойство этого уравнения. Для этого сделаем фазовое преобразование:

f e

X ( x , t ) = exp | i—f ( x , t ) l^ ( x , t ).

V hc J

При условии, что функция f (x, t) удовлетворяет волновому уравнению, функция ^(x, t) удовлетворяет уравнению следующего вида ih

1 e U 1⁵ f

1--21 Ф + —~ mc V c dt dL- hL v^+ dt    2 m

+ ^ihe A - ( v f ) ] ( V^ ) + e | ф+ ^{1 f} k + mc                   V c 8 t J

1 J 2 +---n ee 2 mc ²

⁽ A ^-(v f no- c J

, 2 d2 L

^{+ h} A/2 I ^ '

8 t I

Проводя анализ полученного уравнения, видим, что оно совпадает с предыдущим уравнением (41), но при этом изменились выражения для электромагнитных потенциалов, входящих в данное уравнение. Однако, как было отмечено выше, такое преобразование для электромагнитных потенциалов не приводит к изменению выражений, описывающих электрические и магнитные поля в системе.

Пренебрегая в выражении (43) последним членом в фигурных скобках (в связи с делением на c ² его вклад в общую сумму мал), получим уравнение движения для заряженной частицы в электромагнитном поле в более простом виде:

ih ^f1 — ^{e Ф}Г'||r = - h"" V 2 X + e Фx + ” A P X - (44) V mc J 8 t 2 m mc

Для носителей заряда в кристалле ф - электрический потенциал, A – вектор-потенциал внешнего электромагнитного поля. Наличие в левой части уравнения дополнительного слагаемого позволяет использовать правильную калибровку для электромагнитных потенциалов.

Выражения для плотности заряда и плотности тока в этом приближении имеют вид:

P = e f1 —eФ2 |x| 2,(45)

V mc J e * o'},/ *         2 e 2 I j = — | lxP X l + (x PX)AX l.(46)

2 m VV       J

Представим электрический потенциал в виде ф = ф ₀ + ф ₁, векторный магнитный потенциал - в виде A = A o + A ₁. Здесь ф ₀ и A 0 - потенциалы в отсутствие внешнего электромагнитного поля, ф ₁ и A ₁ – потенциалы внешнего электромагнитного поля. На практике ф ₀ - электрический потенциал внутри атома или внутри кристаллической решётки, обычно в первом приближении полагают, что векторный магнитный потенциал внутри атома и решётки равен нулю A 0 = 0 .

Далее представим решение x в виде

X = Xo +X1,(47)

где x ₀ - решение уравнения (44) при отсутствии внешнего электромагнитного поля:

ih "X° = -    V2Xo + e фо Xo,(48)

d t 2 m а X1 - поправка к решению уравнения при наличии электромагнитного поля:

dv,      h2

ih — = -—V X1 + eфoX1--A1P (X1 -Xo) . (49) dt    2 mmc

В этом случае выражения для плотности заряда и тока имеют вид:

P = Po +P1 +P12,(5o)

j = jo + j1 + jn + ja ,

Po = e|Xo|2, P1 = e| Xj2, P12 = e (XoX*+X1X*) ,

e jo =—llXoP Xo) + |XoP Xo )),

2 m

e j1 =— ((X1P X1 ) + (X1PX1)),

2 m

e j12 =—((XoP X1 ) + (X1P Xo) + 2m

+ (xoP X1 ) + (x* P Xo)), ja =;;— (Po +P1 +P12).

2 mc

В случае слабого внешнего электромагнитного поля уравнения для функций x _o и x ₁ принимают вид:

ih % = -   V2Xo + e ФoXo,(57)

d t2 ih    = - h— V2X1 + e фХ - — A,P Xo.(5

• dt    2 mmc

• 2. Взаимодействие внешнего электромагнитного поля с частицей, находящейся

Выражения для плотности тока и плотности заряда:

P = Po +P12, eA j = j0+ ji2 + :;—(Po + P12).

2 mc

В случае слабых полей уравнения, описывающие взаимодействия электромагнитного поля с носителями заряда, и выражения для плотности заряда и тока становятся линейными относительно искомой функции X 1 .

в постоянном электромагнитном поле

Рассмотрим теперь решение задачи о взаимодействии внешнего электромагнитного поля с частицей, находящейся в постоянном электромагнитном поле. В отсутствие внешнего электромагнитного поля уравнение для скалярной частицы имеет вид, соответствующий (57):

ih    = -h- V2Xo + V)Zo = Ho [xo ],(61)

• d t 2 m

Vo = e Фo,(62)

Ho =-   V2 + e фo.(63)

2 m

Для его решения разделим переменные. Для этого представим решение в виде:

( iE

X o ( ^x , t ) = exp I - — t I F nk ( ^x ) = G nk ( ^x , t ) ,       ⁽⁶⁴⁾

• V h )

где x = ( x 1 , x ² , x ³ ) .

Функция, зависящая от пространственных координат, удовлетворяет уравнению Шрёдингера:

• ( h )

I ^-—^V + e Ф o I F_n k ( x ) = ^E nk ^F nk ( x ) .           ⁽⁶⁵⁾

• V 2 m        )

Общее решение записывается в виде

X o ( x , t ) = Z f nk ( t ) F nk ( x ) = Z g n G ( x , t ) . (66)

При наличии внешнего электромагнитного поля уравнение для волновой функции, представляющей собой добавку к волновой функции невозмущённого состояния, имеет вид, соответствующий (58):

ih    = H o X i + V X o ,                           (67)

• d t

которые использовались для разложения решения невозмущённой задачи:

X i ( x , t ) = E g nk ( t ) G nk ( x , t ) .

Следует отметить, что в этом случае коэффициенты g1nk (t) зависят от времени. Получим уравнение для этих коэффициентов. Подставив выражение для искомой функции в виде разложения по базису, получаем ih Z dFFl G„( x, t )=

= V ( x , t ) Z g 0^m G m ( x , t ) .

Умножив скалярно на G p ( x , t ) , получаем систему дифференциальных уравнений для определения коэффициентов g 1 ^pq ( t ) :

ih dg1= dt

= Z g 0^m ( t )( G p ( x , t ) V ( x , t ) G m ( x , t )}.

, m

Полученное дифференциальное уравнение решается в квадратурах:

t gp (t )=— i ZJ g ‘pvp: (t) dT. h m —m

Матричный элемент, соответствующий внешнему полю, имеет вид:

V mk ( t ) = exp ( -® i'k t ) JJJ F nk ( x ) X

I eI

X I-- A ( x , t )p + e ф ( x , t ) I F lm ( x )d x ,

V mcI

где tonk = — lmlm h V

В итоге решение возмущённого уравнения имеет вид:

A

(

X 1 ^{( x} , t ) = Z ' n , k V

t

t тZJ g‘oV (T)dT Gnk (x, t). him i,m —№                     )

Вычислим матричный элемент взаимодействия, обусловленного наличием векторного магнитного потенциала:

v nk ( t ) = Яf F nk ( x ) ⁽— —A( x , t )p ^A F lm ( x ) d x =

• V    mc )

=jjj Fnk (x) (-mc [jjj a

⁽. ю Л j x exp I i— Z a jx^J

V c j = i

A1 A iюt da1da2dto p х

)J )

X Flm (x)dx = —— f IT A'   exp (—i ю t) х mc

X

(A

Ш F nk ( x ) exp I i~ ^ ^a j X¹ |x

• V    c j=1

х p F_lm ( x )d x ] d a , d a ₂d ю .

Пусть квантовая система находится в точке x ₀ = f x 0 , x 2 , x 0 ^ . Перепишем интеграл (75) в виде:

v - л t ) =

e

=--A 1 2 exp(-imt)expI i — Vajx0 |x mc( c j=1J

X

F n ( x + x ₀)exp I i ^m £ a x lx

( c j=1J

x p F m ( x + x ₀)d x ] d a 1 d a ₂d m .

Так как значения модуля волновых функций резко убывают при удалении от точки x ₀ , то аргумент экспоненты внутри квадратных скобок близок к нулю, а, следовательно, сама экспонента примерно равна единице. Тогда вместо (76) запишем:

v Пк( t ) = -—iJJa”*"2" exP (- i mt )x mc f m)

x exp I i— V " j x 0 | p - d " 1 d a ₂d m ,

I c j=1       J где матричный элемент оператора импульса:

⁽ P q ) nk = JJJ F ^{( x} ) P q F im ^{( x ) d x} .

Вычисление выражения (78) можно свести к вычислению матричного элемента оператора координаты. Тогда расчёты упрощаются, так как в этом случае отсутствует операция пространственного дифференцирования волновой функции. Используем соотношение

- im [ h , x q h

q ^,

которое представляет собой уравнение Гейзенберга для оператора координаты. Используя (79), получаем выражение для матричных элементов оператора импульса через матричные элементы оператора координаты:

nk                    n\nk

^P q ) ,m =- im ( “ - ) ( x ) 1m '                      ⁽⁸⁰⁾

( x ) n^k =Ш ^F nk ( x ) x q F m ( x ) d X .                  (⁸¹)

Тогда

( v . ) - W =

= ie [“nk)( x') n- № A’ "1- exp (-imt )x f-mjL x exp I i—V" jx 0 | da1da 2dm.

Матричный элемент взаимодействия, обусловленный наличием скалярного потенциала:

v-k (t)=e Ш *a1“2m exp (- im t)x x exp I i—V"yxj | Uk (t )d"i d"2 dm, I ci=1     J

где

U -k ( t ) = JJJ F nk ( x ) Ф ( x , t ) F - ( x ) d x .             (84)

Заключение

В работе получено приближённое решение системы уравнений, которая представляет собой систему уравнений Максвелла и уравнения Клейна–Гордона. Приведённые результаты являются фундаментальными для работ, посвящённых взаимодействию электромагнитного поля со структурами пониженной размерности. Особенностью приведённых формул является то, что они приведены в системе СГС, которая часто используется в электродинамике, а не в планковской системе единиц (h=c=1), которую обычно используют в своих работах физики-теоретики и специалисты по теории поля. Это позволяет, в свою очередь, использовать полученные формулы для решения практических задач в единицах, понятных для специалистов в других областях физики.

Работа выполнена при поддержке грантов РФФИ №№ 11-07-12036,11-07-00153,   10-07-00553,   10-07

00109, гранта Президента РФ № НШ-4128,2012,3 и ФЦП «Кадры» (соглашения №№ 8027, 8231).