Современный алгоритм защиты информации
Автор: Гайворонский В.А.
Журнал: Экономика и социум @ekonomika-socium
Рубрика: Информационные и коммуникативные технологии
Статья в выпуске: 3-4 (12), 2014 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/140108882
IDR: 140108882
Текст статьи Современный алгоритм защиты информации
Криптография – это наука о обеспечение скрытности, секретности, передаваемого сообщения между пользователями.
Все современные алгоритмы шифрования используют ключи, для шифровки и дешифровки передаваемой информации, для того, чтобы информация из сообщения стала доступна, необходим ключ. Ключ шифровки и дешифровки может не совпадать, что придает сообщению еще большую надежность.
Алгоритмы шифрования делятся на две крупные группы: алгоритмы с секретным ключом (симметричные) и алгоритмы с открытым ключом (ассиметричные). Алгоритм с секретным ключом использует один и тот же ключ для шифровки и дешифровки, в свою очередь алгоритм с открытым ключом использует разные, независимые ключи, что не позволяет определить по одному ключу другой.
Алгоритмы с открытым ключом позволяют держать ключ для шифровки в открытом виде, чтобы обеспечить любому пользователю зашифровку сообщения. При этом ключ дешифрования будет доступен только тому, кто должен прочитать сообщение. Ключ для шифрования носит название открытого ключа. А ключ для дешифрование называется секретным ключом.
Абсолютно все современные алгоритмы щифровки/дешифровки являются сложными и нет возможность взломать их вручную, из-за трудоемкости и объема вычислений. Все алгоритмы разработаны так, что они могут использоваться только при использовании компьютеров или различных специальных технических средств. Самым лучшим алгоритмом шифрования с открытым ключом на сегодня является алгоритм RSA [1].
Одной из важных задач криптографии является задача разложения числа на простые множители. Трудоемкость решения задачи позволила создать криптосистему RSA.
В 1977 году, в журнале Scientific American, была опубликована статья, о алгоритме шифрования, основанного на идее двух ключевого шифрования. Авторами этой стать стали трое ученых Массачусетского Технологического университета: Рональд Райвест, Ади Шамир и Леонард Адлеман.
Криптосистема получила имя RSA, название состоит из первых букв фамилий авторов.
Суть их метода заключается в следующем: существует известный параметр – целое число n большой длины (например, 2048 бита), которое является произведением двух простых чисел, которые в свою очередь являются секретными параметрами метода. Для взлома системы достаточно знать множители числа n.
На момент публикации, науке было известно несколько методов факторизации, но данные методы не позволяли быстро раскладывать числа, состоящие более чем из 20 цифр, и именно благодаря этому, алгоритм RSA обеспечил безопасность шифрования данных, так как при использовании числа с большим количеством цифр, алгоритм было практически невозможно взломать.
Толчком к развитию в данной области стала публикация, в том же журнале, о взломе 129-значного целого числа, пообещав за его разложение вознаграждение. Интерес подогрела статья математика Мартина Гарднера, под названием «Новый алгоритм, на взлом которого уйдут миллионы лет». Благодаря этому по всему миру начались разработки различных алгоритмов факторизации числа, в итоге мир получил наиболее быстрые алгоритмы разложения: метод квадратичного решета, метод эллиптических кривых, метод решета числового поля, а также метод Полларда.
Сама же задача, поставленная учеными, была решена в 1994 году. Для ее решения потребовалось более около полу года времени, а также сеть, состоящая из более 1600 компьютеров, в результате задача была решена при помощи метода квадратичного решета, коллектив получил свою награду в $100 долларов, обещанное вознаграждение от создателей. На сегодня рекордом является факторизация числа RSA-768, которое имеет 232 знака, и было разложено в декабре 2009 года.
Актуальностью является тот факт, что на сегодня не существует достаточно быстрых алгоритмов разложения больших чисел. Следует учитывать обстоятельство, что очень большие числа (более 232 знаков), до сих пор не факторизованы.
Начиная с 1977 года, после создания алгоритма RSA, наука получила толчок к развитию различных алгоритмов факторизации. Основной проблемой существующих алгоритмов была низкая скорость работа, а также невозможность раскладывать большие числа, вследствие чего возникла проблема, которую в дальнейшем и решили ученые. На сегодня существует две больших группы разложения чисел: экспоненциальные алгоритмы и субэкспоненциальные алгоритмы. Такое разбиение произошло из-за различной сложности алгоритмов[1].
В экспоненциальные алгоритмы входят:
-
- перебор делителей;
-
- метод Ферма:
-
- р-алгоритм Полларда;
-
- р-1 алгоритм Полларда;
-
- метод квадратичных форм Шенкса;
-
- метод Лемана.
Сложность всех этих алгоритмов зависит от длины самого числа, из-за этого группа методов и получила такое название. Первые два метода являются наиболее ранними, а также наиболее долгими по времени выполнения.
Вторая группа алгоритмов, субэкспоненциальные, в нее входят:
-
- алгоритм Диксона;
-
- метод непрерывных дробей;
-
- метод квадратичного решета;
-
- метод эллиптических кривых.
Скорость работы этих алгоритмов является более быстрой, все эти алгоритмы являются наиболее современными и наиболее используемые в настоящее время[1].
Наиболее эффективным алгоритмом является метод квадратичного решета, именно благодаря этому методу была впервые решена задача разложения 129-значного числа, поставленная в 1997 году. Он является самым эффективным методом вплоть до 169 значений входного параметра. Но тем не менее следует не забывать, что в настоящее время стоит задача разложение еще более больших чисел, поэтому самым эффективным методом является метод решета числового поля. Он менее эффективен до 169 знаков во входном параметре, по преодолев данный порог, он является самым быстрым на сегодняшний день[2].
Сегодня существует ряд RSA чисел, которые ученые до сих пор не смогли разложить. Данные числа являются достаточно интересным примером для разработки эффективных алгоритмов, так как решение данной задачи поставит под сомнение использования современного алгоритма RSA в качестве шифрования сообщений.
Как было сказано в ранее, первым алгоритмом был – алгоритм перебора. Он имеет историческую ценность, так как является одним из основополагающих алгоритмов разложения.
Кратко алгоритм выглядит следующим образом: при помощи решета Эратосфена создается база простых чисел, после чего входной параметр поочередно делится на каждое из них, до тех пор, пока не достигнем единицы на выходе.
Алгоритм является крайне простым в план реализации, но рассматривается в данном случае, как демонстрация одного из первых алгоритмов факторизации.
Опишем реализацию алгоритма. Изначально надо реализовать решето Эратосфена (Эратосфен родился в Греции, в третьем веке. После себя он оставил достаточно большие труды в области истории, литературы, математики, но наиболее значимые работы были в области географии. Именно он впервые определил длину экватора, ошибившись всего на 430 километров. Введем понятия простых и составных чисел). Простым называется такое число, которое имеет только два делителя, это единица и само это число, например, 7 можно разделить только на 1 и само себя. Составными числами называются все остальные, которые имеют более двух делителей. Единица не относится ни к одной из групп, так как имеет только один делитель.
Метод решета Эратосфена получил свое названия из-за схожести с операцией просеивания, через решето проходят все числа, и просеиваются только простые числа, исключая все остальные. В начале алгоритма определяются границы просеивания, логично предположить, что начальной точкой просеивания будет является двойка, так как на единицу делятся абсолютно все числа. Так же логично предположить, что конечной точкой будет сам входной параметр, но основываясь на том, что алгоритм сам по себе является долгим в плане времени исполнения, поэтому логично предположить, что крайним числом в решете будет квадратный корень из входного параметра, проще говоря Тп.
После того как были определены границы просеивания следует операция поочередного деления всех чисел друг на друга, начиная с самого первого, если число делиться, то оно вычеркивается и в дальнейшем не используется, повторяя данную операцию для все оставшихся чисел, мы выделим только те, которые делятся только на 1 и само себя, то есть будут все простые числа в определенных границах.
Алгоритм можно представить в следующем виде:
int[] eratosfen = new iпt[(int)(n-1)];//массив для решета эратосфена for(int i=0;i for(int i=2;i<=n;i++) { k=0; if ((eratosfen[j]%i )==0) eratosfen[j]=0; } ___________________}______________________________________________________________________________________________ Листинг 1 - Реализация решета Эратосфена Из листинга видно, что алгоритм достаточно прост, и его скорость выполнения зависит от длины границы решета. В результате можно получить следующее: при определении простых чисел, обозначив границы от 2 до 50, на первой итерации получим результат представленный на следующем рисунке. Рисунок 1 - Работа решета Эратосфена на первой итерации Следовательно, получается ряд простых чисел: 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47. Результат работы алгоритма можно представить в виде таблицы простых чисел. Таблица 1 Простые числа в промежутке от 1 до 00 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 10 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 67 683 691 701 709 719 727 733 739 743 751 757 761 769 773 781 787 Следующим шагом алгоритма является реализация деления, входного параметра на все простые числа в списке. Алгоритм довольно прост, необходимо делить поочередно входной параметр на простые числа, пока не будет достигнута единица в итоге. Скорость работы алгоритма зависит от размера простых делителей числа, чем меньше они, тем быстрее будет работать алгоритм. Алгоритм представлен в виде уже реализованного отрезка приложения, которое требуется разработать по окончанию выполнения выпускной квалификационной работы. Здесь не используются специальные типы данных, позволяющие вводить число любой длины, это сделано специально, с учетом того, что когда алгоритму будет предложено разложить число максимально допустимой длиной стандартного целочисленного типа Long, данный метод уже потеряет эффективность, и будет достаточно долго вычислять необходимы делители, поэтому здесь рассматривается вариант, при котором типом данных является Integer или Long (длина ключа составляет 32 или 64 бита). Результатом работы алгоритма является вывод произведения всех простых множителей, которые образуют данное число. В заключении следует отметить что был разобран алгоритм перебора простых чисел при помощи решета Эратосфена, были показаны некоторые отрезки кода, которые необходимы для понимания и дальнейшего использования алгоритма. Следует отметить, что алгоритм RSA является одним из самых защищенных на сегодняшний день и имеет очень большую во всех сферах, где необходима передача информации.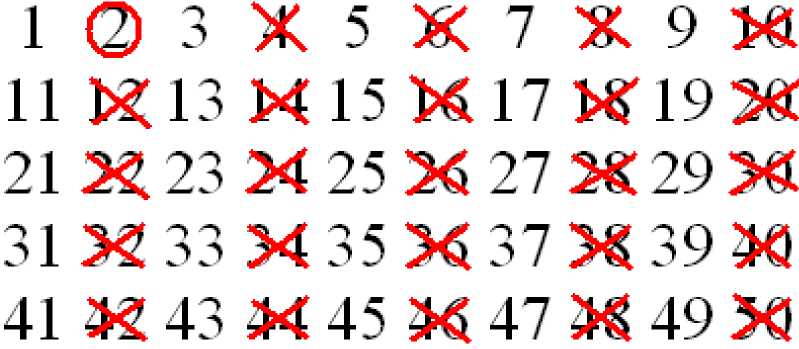
Список литературы Современный алгоритм защиты информации
- Ишмухаметов, Ш.Т. Методы факторизации натуральных чисел : -Казань, Казанский универстиет, 2011 г. -190 с.
- Бехроуз, А. “Интуит” -математика криптографии и теория щифрвания : -Режим доступа: http://www.intuit.ru/studies/courses/552/408/lecture/9368?page=6


