Современный подход к проектированию торцевых зубчатых передач и измельчителей материалов на их основе

В работе [1] показано, что одним из самых эффективных способов измельчения является измельчение в закрытом объеме при совместном воздействии на материал сжатия и сдвига. Наиболее полно этот способ реализуется в измельчителях, исполнительный механизм которых выполнен на основе торцевой зубчатой передачи (ТЗП).

Одним из основных моментов при создании таких измельчителей является проектирование геометрии ТЗП.

В [2] приведен анализ предыдущих работ по проектированию геометрии ТЗП, который выявил следующее:

– синтез геометрии выполнялся на основе метода профильных нормалей путем сочетания математических расчетов координат точек и построением по ним профиля вручную, хотя известен другой более эффективный метод, основанный на теореме Гофмана, но он не применялся из-за недостаточно развитого в то время программно-математического обеспечения;

– из-за особенностей метода профильных нормалей затруднен поиск рациональной геометрии, автоматический синтез профилей колес передачи;

– полученные ранее результаты по проектированию геометрии несовместимы с современными CALS-технологиями создания машин.

Таким образом, перед нами стала задача по реализации современного подхода к проектированию геометрии и созданию на основе ТЗП измельчителей материалов.

Как показано выше, существующие подходы к проектированию геометрии ТЗП не позволяют создать процессорные модули для вычислительных пакетов типа COSMOS, ANSYS и т. д., а также их использование в сис- темах автоматического проектирования [3]. В работах [4; 5] рассматривается способ апроксимационного решения задач профилирования (как прямой, так и обратный) без вычисления нормалей и скоростей относительного движения по единому алгоритму для любых форм описания исходного профиля.

Используя методику, изложенную в работах [3–5], решим задачу по проектированию геометрии ТЗП.

Нахождение сопряженного профиля можно представить в виде схемы: известен (задан) рабочий профиль зубьев одного из колес ТЗП, требуется найти профиль зубьев сопряженного колеса. Он может быть задан аналитически или в виде последовательности точек. В последнем случае необходимо использовать сплайн-апроксимацию.

Составим свод формул для преобразования координат заданного исходного профиля зубьев одного из колес в координаты другого колеса передачи. При этом сложное движение представим в виде сочетания простейших движений: прямолинейного переноса и поворота коор- динатных систем относительно друг друга.

Пусть зубья колеса выполнены с плоскими рабочими поверхностями, а шестерни – с выпуклыми поверхностя- ми, которые характеризуются тем, что рабочие поверхности шестерни образованы кривой, сопряженной к ли- нии – образующей рабочий профиль зубьев колеса.

После преобразований в координатной форме фор- мулы перехода от системы колес Sk к системе шестерни Ssh примут следующий вид:

x_sh = x k cos R V + y k sin R V - a sin V ; y h = — x k sin R V + y k cos R V — a cos V ,

Вестник Сибирского государственного аэрокосмического университета имени академика М. Ф. Решетнева

rk где R =--1; a = r - r - межосемое расстояние; r - rsh делительный радиус шестерни; rk – делительный радиус колеса; v — угол обката шестерни; xsh, ysh - координаты любой точки профиля колеса в системе координат шестерни; xk,yk – координаты любой точки профиля колеса в системе координат колеса.

Для простоты будем рассматривать данную задачу как плоскую – в сечении, перпендикулярном осям вращения колеса и шестерни при заданном значении высоты зуба колеса, например в среднем сечении. Схема преобразования систем координат колеса в систему координат шестерни в процессе обката показана на рис. 1. При условии обката по делительным окружностям колеса и шестерни без проскальзывания, v — угол обката шестерни, ф - угол обката колеса.

Для поиска точки сопряжения между кривыми, образующими профиль зуба и его выкружки необходимо решить систему следующих уравнений:

^хь ⁺ У ь = ^rkb ;

^x ь ( v ) = x p ( ^un )^{- cos} ( ^R v ) +

+ y_k ( un + a ) • sin ( R v ) - a sin ( v ) ;

^

Уь (v) = -x(un)- sin (Rv) +

+ y_k ( un + a ) • cos ( R v ) - a cos ( v ) ;

X p ( u ) = u • tga + P

У р = u - a ,

где

P₁ = r_k ( sin p- cos p ) - tg a ;

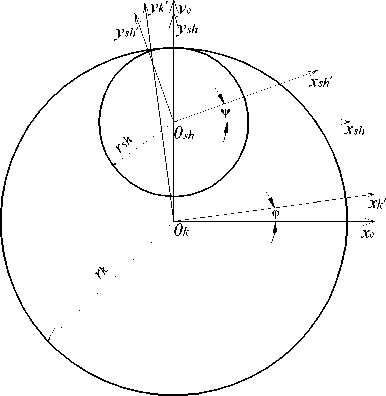
Рис. 1. Преобразование систем координат колеса и шестерни в процессе обката

^X 1,2

- 2 • c₁ y_p ( un + a ) ± 2 x_p ( un ) • ^ x p ( un ) + y p ( un ) - c 2 • [ x p ( un ) + yp ( un + a ) ]

c i =

r kb - x p ( un ) - y p ( un + a ) - a ²

2 • a

arccos ( x ₁₂ )

v =----——

R - 1

.

Для точки пересечения профиля зуба с окружностью вершин следует решить систему уравнений:

^хь ⁺ y b = r ka ;

xsh

( v ) = cos ( R v + a ) • P₁ + a sin ( R v + a ) • P ₂ ( v ) R

x cos ( a ) - a sin v;

y ^ ( v ) =

- sin ( R v + a ) • P + a cos ( R v + a ) P ₂ ( v ) R

Радиус обката принимается равным делительному радиусу шестерни. Чтобы получить реальный боковой профиль зуба необходимо найти огибающую семейства траекторий. За исходный профиль возьмем правую половину зуба колеса (рис. 2).

Формула линии профиля зуба колеса в системе коор-

x cos ( a ) - a cos v;

^x 1,2

динат колеса в параметрическом виде выглядит следую-

щим образом:

Xk = u • tg a + r_k ( sin р- cos р- tg a ) ;

. Ук = ^u ,

где и - вспомогательный параметр; a - угол профиля зуба колеса; Р - угол, соответствующий длине дуги, равной половине ширины зуба колеса.

Уравнения кривой рабочей части профиля зуба шестерни, являющейся сопряженным профилем к профилю зуба колеса в параметрической форме имеет вид xsh (v) = rk sin (a - в) cos (R V+a) +

<

a

+—sin R

( R v + a ) cos ( R v + a - v ) - a sin v;

y_S h ( v ) = ^- r k ^sin ( ^{a - e} ) ^sin ( ^R v ^{+ a} ) +

+ RR cos ( R v + a ) cos ( R v + a - v ) - a cos v, где v - основной варьируемый параметр - угол обката, радиус обката принимается равным делительному диаметру шестерни; a - угол профиля зуба колеса.

P₂ = tg a^ sin ( v- R v ) + cos ( v- R v ) ;

_{2     2/ x} ( 1 - 2 R ) ₂

2 a • cos a^ P ± 2 a •.. P ² cos² ( a ) ----- —-• c²

11     _R 2

² • Re ( ¹ - ² R )

_a 2            ₂

где с 2 = r ka ^- P ^2cos ( ^a )^- 7? ( ^{1 - 2 R} ) ;

R ₂

arcsin (x12) + a v =----x ’ —

1 - R

.

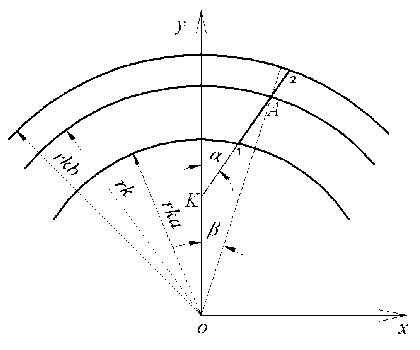
Рис. 2. Профиль зуба колеса в среднем сечении в системе координат колеса

Графики траекторий точек колеса и шестерни в зацеплении, полученные по описанным выше формулам, представлены на рис. 3.

На основе произведенных расчетов было синтезировано зацепление шестерни и колеса (рис. 4).

Рассмотренная выше методика проектирования ТЗП позволяет получить разнообразные варианты сочетаний сопряженных профилей и выбрать из нихнаиболее рациональный, например, по критерию технологичности.