Создание цифрового двойника процесса сборки рабочего колеса компрессора

Заданная степень повышения давления, устойчивость и надежность работы компрессора зависит от обеспечения равномерности сборочных параметров между лопатками [1]. В рабочем колесе (РК) компрессора 8 ступени ключевым сборочным параметром является величина натягов между антивибрационными полками лопаток. Обеспечения равномерного натяга является при ремонте и использования двигателя в качестве наземной силовой установки первостепенной задачей, так как требуемый ресурс работы компрессора возрастает в 2-3 раза. На рисунке 1 приведена модель рассматриваемого рабочего колеса компрессора.

Из-за недостаточного или излишнего напряжения между лопатками, а также его неравномерности лопатка становится излишне вибронагруженной, начинает колебаться и разрушается, обломки лопаток в процессе работы двигателя разрушают остальные лопатки диска, а кроме того, и лопатки нескольких дисков за ним. На рисунке 2 приведена фотография РК со сломанными лопатками, не прошедшего испытания.

Равномерность натягов по антивибрационным полкам обеспечивается точностью изготовления лопаток и их сборкой. Сужение допусков на изготовление экономически не целесообразно [2]. Существенным резервом повышения эксплуатационных показателей является улучше-

ние технологии сборки лопаточных венцов. При ремонте рабочего колеса выполняют предварительные расстановки лопаток, стремясь достичь лучшего результата, что является ресурсоемким процессом с множеством испытаний. Учитывая, что число лопаток в рассматриваемой ступени 84, число комбинаций принимает огромное значение, равное факториалу от числа лопаток.

Высокотехнологичная промышленность нового поколения основана на использовании цифровых данных для повышения качества и снижения сроков выведения изделий на рынок. Основой для такой промышленности является разработка цифровых двойников (ЦД) изделий. Применительно к рассматриваемому рабочему колесу, цифровой двойник – цифровая копия физического колеса в собранном состоянии, помогающая обнаруживать проблемы со сборкой, предсказывать результаты сборки и получать более точные результаты по натягам между лопатками. Применение компьютерного моделирования [3] и прогнозирования результирующих сборочных параметров [4] рабочего колеса возможно за счет использования современных средств измерений, позволяющих достаточно точно воспроизводить объекты разных габаритов и сложности [5].

В настоящее время существуют все возможности учитывать данные, поступающие с контрольно-измерительных операций лопаток [6, 7], и на основании этих данных строить математические модели расчета сборочных параметров [8] и производить сборку быстро и с требуемым качеством [9]. Цифровое моделирование позволяет осуществлять метод индивидуального подбора деталей в сборках [10, 11].

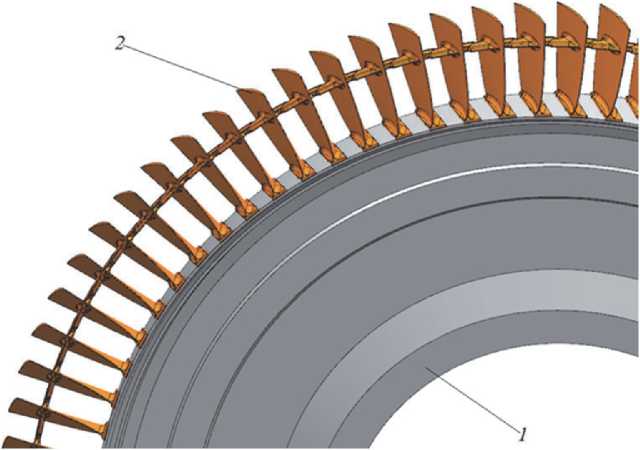
Рис. 1. Конструкторская модель рабочего колеса 8 ступени: 1 - диск; 2 - рабочая лопатка

Рис. 2. Не прошедшее испытания рабочее колесо

Целью исследования является создание цифрового двойника процесса сборки рабочего колеса 8 ступени компрессора, позволяющего производить расчет углов закрутки лопаток, характеризующих натяги между антивибрационными полками рабочих лопаток. Для повышения скорости получения результатов расчетов сделано их обобщение с помощью использования подходов машинного обучения, в частности, метода случайного леса [12].

ЦИФРОВОЙ ДВОЙНИК ДЛЯ РАСЧЕТА УГЛОВ

Номинальные размеры и допуски на изготовление лопаток предполагают наличие натяга между антивибрационными полками, его величина определяется конструктором. Натяги определяются сочетанием геометрических от- клонений соседних лопаток, а также геометрическими отклонениями пазов диска, в которые они вставляются. Натяги в технологическом процессе контролируются в двух сечениях (рисунок 3) специальными приборами - угломерами: измеряется угол установки лопаток у:. в свободном и собранном состояниях; разница этих углов v. . характеризует величину натяга в соединении."

Согласно технологии изготовления, и на диске, и на лопатках проводится контроль геометрических параметров, характеризующих их качество.

На диске производится контроль пазов, ключевыми параметрами при их контроле являются: углы разворота пазов (между осью вращения диска и осями симметрии пазов) 3. ; величины углов деления пазов 5;,, . ' "

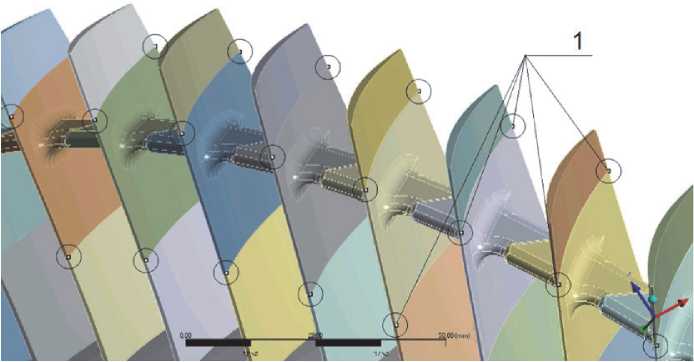
Рис. 3. Расположение контролируемых точек (1) на пере лопаток

При контроле лопаток в производстве измеряют: a) отклонение величин стыковых размеров по рабочим торцам антивибрационных полок лопаток ( ^sp ) со стороны спинки 51^ и корыта Sip ; б) фактические значения угла касательной к профилю в контрольных сечениях лопаток в свободном состоянии ( Уь) .

После измерений выполняется расчет отклонений измеренных параметров p от параметров , заданных по чертежу:

^as Pmeas Pt . (1)

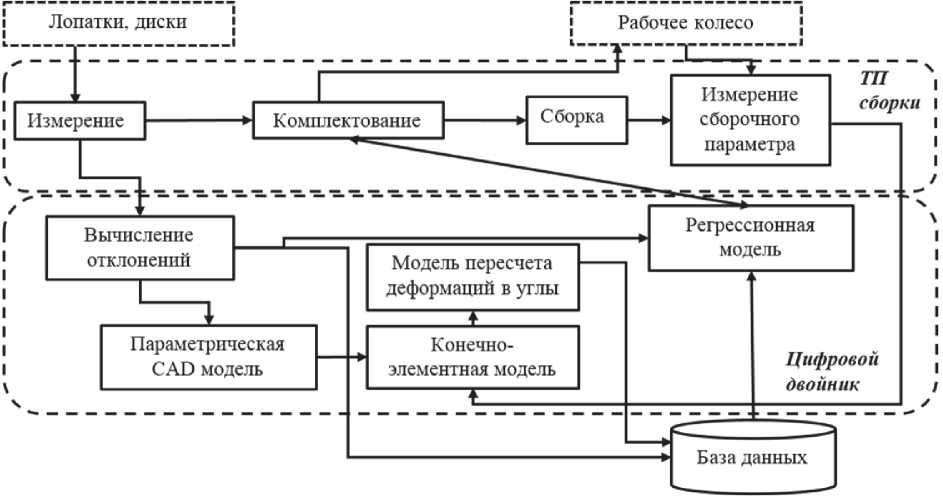
Рассмотренные выше отклонения и план расположения лопаток в комплекте используются на входе в цифровой двойник для расчета значений возникающих натягов (характеризуемых Уь н). На рисунке 4 приведена архитектура цифрового двойника процесса сборки рассматриваемого РК и его место в технологическом процессе (ТП) сборки.

Основными этапами процесса сборки РК являются: 1) измерение геометрических параметров лопаток и дисков; 2) комплектование лопаток в РК; 3) сборка РК; 4) измерение сборочных параметров РК. На вход технологического процесса сборки РК поступают лопатки и диски. На выходе технологического процесса формируются РК. Повышение управляемости процессом сборки рабочих колёс возможно посредством выработки рациональных решений по комплектации и раскладке лопаток с использование ЦД. Между ЦД и технологическим процессом сборки предусмотрены прямая и обратная связи.

Прямая связь предусматривает передачу информации из ЦД в операцию комплектования ТП. Передаваемая информация содержит данные по рассчитанным отклонениям углов Yb m , характеризующих возникающие натяги в соединениях между лопатками. Использование численного

।                                                                ।

Рабочее колесо

Модель пересчета деформаций в углы

Цифровой двойник

ТП х сборки

Конечноэлементная модель

1 п                              !

Лопатки, диски

Регрессионная модель

Измерение сборочного параметра

Параметрическая CAD модель

База данных

Вычисление отклонений

Комплектование

I Измерение

Сборка

Рис. 4. Архитектура цифрового двойника процесса сборки рабочих колёс

моделирования с использованием ЦД позволит принимать решение по улучшению комплектации (уменьшению неравномерности натягов) без многократных пересборок и измерений углов комплектов.

Обратная связь предусматривает передачу информации об измерениях геометрических параметров лопаток, дисков и рабочих колёс в ЦД для уточнения параметров моделирования при разработке модели.

ЦД включает в себя процедуру расчета отклонений параметров и комплекс моделей: параметрическая CAD-модель; конечно-элементная модель расчета деформаций; модель пересчета деформаций в углы установки; регрессионная модель, основанная на методе машинного обучения. Результаты рассчитанных углов и отклонений накапливаются в базе данных, информация из которой используется для обучения регрессионной модели. Рассмотрим разработанные модели, входящие в ЦД.

ПАРАМЕТРИЧЕСКАЯ CAD-МОДЕЛЬ

Параметрические модели лопаток созданы в программе NX. В модели упрощен хвостовик и пазы диска, осуществляется сдвиг и разворот торцевых контактных плоскостей антивибрационной полки. Кроме того, можно изменять угловое положение лопаток согласно погрешности деления пазов ^чч . На рисунке 5 приведен эскиз модели с обозначенными параметрами геометрических отклонений, которые можно вносить в модель.

КОНЕЧНО-ЭЛЕМЕНТНАЯ МОДЕЛЬ В ANSYS

Расчет изменения углов установки пера можно выполнить с использованием конечно-элементных моделей (КЭМ) в среде ANSYS. Создание конечно-элементной модели, как отмечалось выше, выполнялось в системе ANSYS Workbench, с использованием модуля Static Structural. Этапы формирования КЭМ: 1) задание механических свойств; 2) импортирование и связка параметризованных моделей лопаток и диска; 3) задание граничных условий; 4) задание выводимых параметров в препроцессоре.

Механические свойства материалов задавались исходя из материала лопаток рабочего колеса. Для выполнения КЭ моделирования сборки рабочего колеса задавались следующие механические свойства материала диска и лопаток: коэффициент Пуансо -на –0,36; модуль нормальной упругости 9,6 ^. 10¹⁰ Па; плотность материала 4620 кг/м³; предел прочности 1,07 ^. 10⁹ Па; физический предел текучести 9,3 ^. 10⁸ Па; условный предел текучести 9,3 ^. 10⁸ Па; коэффициент теплового расширения 9,4 ^. 10^{–6 о}С^–1.

Для автоматизации задания параметров модели (геометрических отклонений, измеренных на деталях или сгенерированных) в пакете MATLAB был написан скрипт, управляющий процессом в ANSYS с помощью отправки APDL команд. Скрипт так же позволяет автоматически сохранять результаты расчетов. Исходные геометрические параметры лопаток загружаются из файла формата *.xlsx. После расчета величины деформаций вдоль координатных осей для контрольных точек экспортируются в формате *.txt.

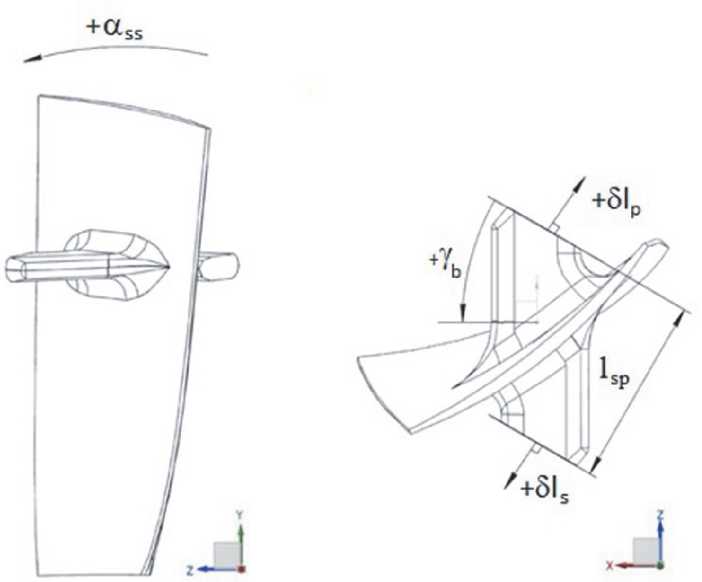
Рис. 5. Эскиз модели рабочей лопатки с параметрами отклонений

МОДЕЛЬ ПЕРЕСЧЕТА ДЕФОРМАЦИЙ В УСТАНОВКИ

Для расчета углов Yb из величин координат контрольных точек была разработана математическая модель, реализованная в среде MATLAB. Она позволяет преобразовать деформации, полученные из КЭМ, и координаты исходных точек геометрической модели в углы установки профилей. В результате для каждой лопатки рассчитываются величины изменений углов установки профилей.

На первом этапе координаты контрольных точек из конструкторской модели сохраняются в матрицу ^84X3. Значения деформаций точек на профиле лопаток вдоль трех осей последовательно загружаются и сохраняются в одну матрицу деформаций ^84X3 .

На втором этапе производится расчет координат точек на профиле лопаток после сборки, то есть когда лопатки контактируют друг с другом по антивибрационным полкам. Для этого необходимо просуммировать массив координат точек до сборки с массивом значений деформаций по правилу сложения матриц, получив матрицу :

@84x3 ~ ^84x3 + ^84x3 . (2)

Для выполнения расчета углов установки следует перейти в двумерную систему координат, что выполняется в два этапа. На третьем этапе преобразование Декартовой системы координат в полярную. За ось вращения примем ось двигателя X . Остальные две координаты точек в данном случае задаются с помощью угла •P и радиус-вектора p* от центра координат:

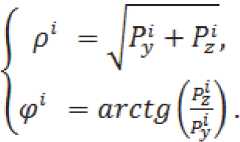
На четвертом этапе из двух полярных координат рассчитаем длину окружности для каждой точки, получив вторую ось X^ новой системы координат:

P'l = P^£ ■ Ф¹ № . (4)

На заключительном этапе в полученной плоской системе координат выполняется непосредственно расчет угла касательной к профилю лопаток Yb . Из координат точек вычисляются уравнения прямых, из уравнения прямых – углы наклона к оси X. Угол касательной до сборки на- ходится аналогично.

Далее вычисляется разность этих углов и, таким образом, получается угол между двумя прямыми – изменение угла

Yb , характеризу-

ющий разворот лопатки и возникающий натяг в соединении.

РАССМАТРИВАЕМЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ

Расчет в КЭМ длится долго (для комплекта из 84 лопаток около двух часов на персональном компьютере с процессором AMD Ryzen 7 2700 Eight-Core с тактовой частотой 3,2 ГГц), требует долгой настройки и поэтому данный расчет проблематично использовать в производстве.

Моделирование посредством ANSYS случаев сборки используется для генерации выборки, достаточной для создания регрессионной модели, в которой на входе будут значения отклонений лопатки и двух ее соседей, на выходе величина угла разворота этой лопатки. Для построения регрессионной зависимости использовались методы машинного обучения: метод опорных векторов (SVM) [13], гребневая регрессия (KR) [14] и случайный лес (RF) [12]. Из трех методов выбирался лучший с точки зрения получаемой в прогнозе ошибки.

Оценка ошибок прогнозирования угла производится по трем критериям: доля спрогнозированных величин в пределах допустимой погрешности δ (количество случаев, не превышающих определенный порог), среднеквадратичная ошибка MSE и коэффициент детерминированности R ². Допустимая величина ошибки была выбрана 10 угловых минут, или 0,167 °.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Экспериментальные исследования включили в себя: апробацию разработанной конечноэлементной модели, используемой для создания обучающей выборки регрессионных моделей; проведение обучения трех моделей регрессии и выбор лучшей.

Используя результаты измерений лопаток для комплекта рабочих колес, было выполнено моделирование их сборки с использованием разработанной конечно-элементной модели. Углы были проанализированы и проведено их статистическое обобщение, а именно вычислено минимальное ^min , максимальное ^max значение, математическое ожидание /^ и среднеквадратическое отклонение .

Рабочее колесо было собрано, с использованием угломера были измерены углы Yb , и, соответственно, их разность Y ь m до и после сборки.

В таблице 1 приведены статистические характеристики углов Y ь m , полученных в эксперименте и рассчитанные с использованием КЭМ модели ЦД (математические ожидания, среднеквадратические отклонения, минимальные и максимальные значения).

Таблица 1. Статистические характеристики углов

Параметр	Первое сечение			Второе сечение
	Эксперимент	Модель	Погрешность	Эксперимент	Модель	Погрешность
М , °	0,92	0,89	0,04	1,34	1,30	0,03
о , °	0,07	0,03	0,06	0,10	0,08	0,09
Д .   ° mm,	0,75	0,81	-0,11	1,15	1,10	-0,14
^ тах ,	1,07	0,94	0,17	1,66	1,45	0,25

Согласно обобщенным результатам в таблице 1, предельная погрешность модели не превышает 0,17° на первом сечении и 0,25° на втором сечении, или 15 угловых минут.

Основываясь на статистических данных по отклонениям лопаток, была выполнена искусственная их генерация для проведения моделирования достаточной обучающей выборки с использованием цифрового двойника. сего в ANSYS было проведено моделирование 15 комплектов по 84 лопатки в каждом с различными сочетаниями геометрических отклонений лопаток, для того чтобы максимально охватить возможные случаи сборки. Обучающая выборка для прогноза углов каждой лопатки составила 1008 случаев, тестовая 252 случая. Математическое ожидание обучающей выборки μ составило 1,632°, среднеквадратическое отклонение σ составило 0,249°.

В таблице 2 приведены значения минимального , максимального погрешностей прогноза , а так же и для тестовой и обучающей выборок при использовании рассматриваемых методов машинного обучения.

Меньшие погрешности дает модель RF, предельная величина погрешности для тестовой выборки фактически не превышает 0,05° для первого сечения и 0,11° для второго (6,6 угловых минут). При обучении предельные погрешности модели RF не превышают 0,163° (10 угловых минут). В таблице 3 приведены рассчитанные параметры точности прогнозирования с использованием рассмотренных методов машинного обучения для тестовой и обучающей выборки.

Согласно полученным результатам была выбрана модель регрессии с использованием метода случайного леса, имеющего наибольшей коэффициент R ², наименьшую величину MSE и в котором ни один случай не выходит за допустимый предел погрешности в 10 угловых минут, что является хорошим результатом, так как в практике контроля сборочных параметров используют оптические угломеры, цена деления которых составляет 10 угловых минут.

ЗАКЛЮЧЕНИЕ

В результате исследований разработан цифровой двойник, позволяющий прогнозировать изменение углов установки, возникающие из-за контакта антивибрационных полок рабочих лопаток в сборке колеса компрессора, характеризующие натяги в соединении. В цифровом двойнике реализована конечно-элементная модель непосредственного расчета изменения углов, и кроме того обобщающая ее регрессионная модель, основанная на методе случайного леса. Погрешность расчета углов с помощью цифрового двойника не превышает 15 угловых минут, если использовать конечно-элементную

Таблица 2. Статистическая оценка погрешностей прогнозирования

Параметр	Первое сечение						Второе сечение
	SVM		KR		RF		SVM		KR		RF
	Обучение	Тест	Обучение	Тест	Обучение	Тест	Обучение	Тест	Обучение	Тест	Обучение	Тест
М, °	0,002	-0,001	-1-10-4	0,002	-0,002	-3-10-4	0,011	-0,002	-4-10-4	0,008	-0,005	-0,001
О,°	0,049	0,028	0,004	0,049	0,029	0,011	0,056	0,072	0,011	0,061	0,065	0,029
^ mi» °	-0,100	-0,088	-0,021	-0,093	-0,082	-0,040	-0,244	-0,250	-0,059	-0,23	-0,163	-0,106
^ тах , °	0,100	0,062	0,016	0,100	0,052	0,046	0,152	0,173	0,042	0,132	0,146	0,093

Таблица 3. Параметры точности обучения и теста для разных моделей регрессии для прогноза

Метод регрессии Первое сечение Второе сечение δ, % R2 MSE 5 % R2 MSE Обучение Тест Обучение Тест Обучение Тест Обучение Тест Обучение Тест Обучение Тест SVM 1,00 1,00 0,72 0,71 2-10-3 2-10-3 0,99 0,99 0,95 0,94 4-10-3 4-10-3 KR 1,00 1,00 0,91 0,90 8-10-4 8-10-4 0,99 0,99 0,92 0,91 5-10"3 6-10-3 RF 1,00 1,00 1,00 0,98 2-10-5 2-10-4 1,00 1,00 1,00 0,99 1-10-4 8-104 модель. Регрессионная модель позволяет заменить конечно-элементную модель, работающую долго и сложно применимую в практике, однако вносит дополнительную погрешность расчета, не превышающую 10 угловых минут. Прогнозирование ключевого сборочного параметра сразу после контрольных операций позволяет использовать модель для проведения виртуальных расчетов сборочных состояний и подбора лучшего сочетания лопаток до проведения фактических работ по сборкам комплектов рабочих колес.