Создание градиентных покрытий с комплексом свойств, обеспечивающих стойкость к эксплуатационным воздействиям
Автор: Какурин И.Р., Лазарев А.Л., Шорин М.А.
Журнал: Огарёв-online @ogarev-online
Статья в выпуске: 13 т.3, 2015 года.
Бесплатный доступ
Изложены основные принципы метода расчета функционально-градиентных композиционных материалов с покрытием. Приведен пример прогнозирования свойств композита с покрытием, выполненный методом расчета функционально-градиентных материалов с учетом выравнивания напряжений в прослойке.
Прогнозирование свойств, расчет, функционально-градиентные композиционные материалы
Короткий адрес: https://sciup.org/147248888
IDR: 147248888 | УДК: 624.078.44
Текст научной статьи Создание градиентных покрытий с комплексом свойств, обеспечивающих стойкость к эксплуатационным воздействиям
Современные технологии предъявляют к конструктивным материалам повышенные функциональные требования. Существует множество способов получения композитов с заданным распределением свойств. Наиболее перспективными являются слоистые композиты. Формирование слоистой структуры композитного изделия возможно различными способами – приклейка армирующего слоя с помощью клеевых составов, нанесение полимерного состава на поверхность изделия, импрегнация и т.д. [1].
Технология изготовления покрытия оказывают значительное влияние на работу изделия в процессе эксплуатации. Распределение упругих свойств по сечению основного материала и покрытия могут иметь дискретный или градиентный характер, что должно отражаться на методах расчета элементов с покрытием.
При проектировании функционально-градиентных композитов с покрытием необходимо обеспечить надежную работу композита, покрытия и промежуточного слоя [2].
Нормальные напряжения в сечении определяются выражением
N i
F l
+
4Mi bh2 ^ШУпО^
где Ni – осевая сила в каждом составляющем стержне; Mi – внутренний момент в том же стержне; Fi – площадь поперечного сечения i-гoстержня.
С учетом формул [3]
ox = kxf (ц),(2)
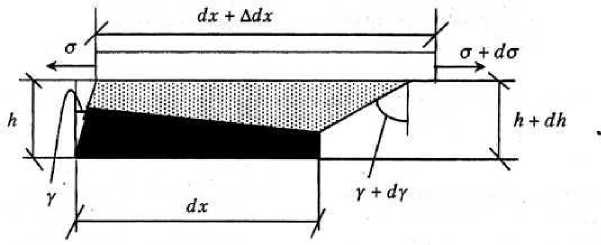
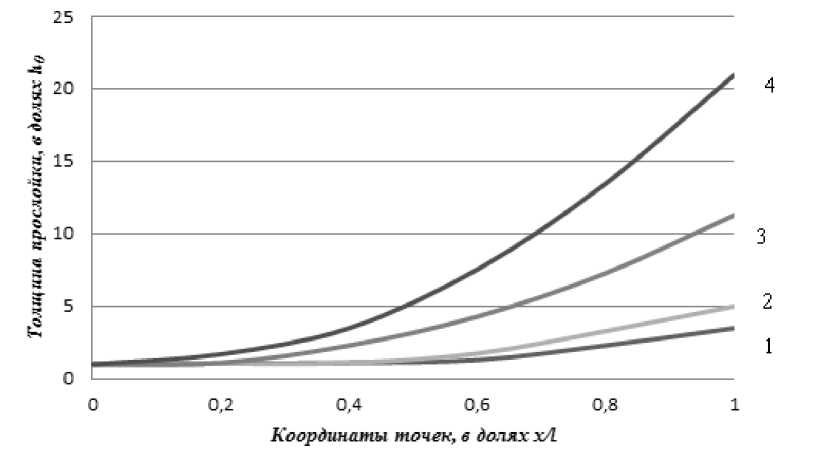
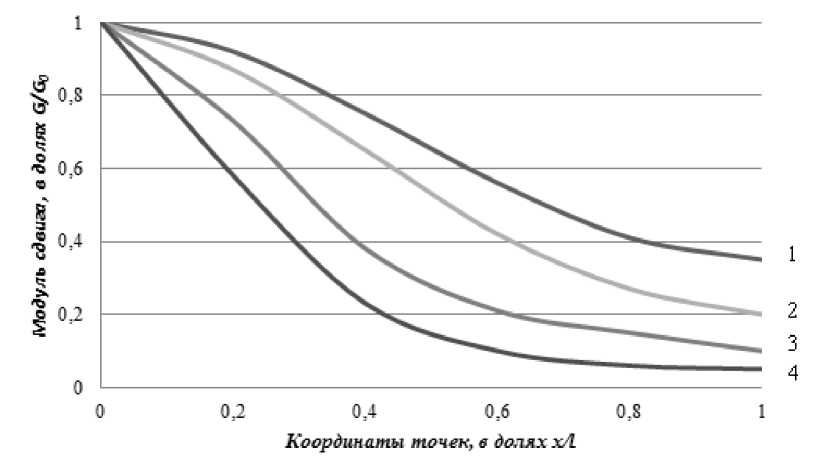
^b внутренний момент в i-м стержне определяется из выражения Mi^E^-Z^T^(4) Здесь ^E] и EJt рассчитываются по формулам ZE] = (h + ]2^E(y')dy; EJt = ]t^?E Предполагаем, что сдвигающие усилия развиваются в промежуточном слое, соединяющей первый и второй стержень. Модуль упругости Екм композиционного материала [4] можно оценить по следующей формуле: Екм = E1Y1 + Е2у2, (5) где Е1, Е2 – модули упругости структур, составляющих композит в каждом слое стержня; γ1, γ2 – их объемное содержание. Учитывая неоднородность элемента по высоте поперечного сечения, принимаем hкак функцию координаты ц (здесь ц = y/h). На основании известных величин модуля упругости вычисляем функции f(^) распределения напряжении. В элементах, где крайние слои выполнены из материала с гораздо большим модулем упругости чем в срединной области, нормальные напряжения изменяются по высоте поперечного сеченияв соответствии с графиком показательной функции f(^) = к(ец — 1). Эффект от покрытия наблюдается лишь при его совместной работе с основным материалом, что говорит о необходимости уделять особое внимание при расчете таких конструкций возникающим в контактном слое напряжениям и отслоению покрытия. При работе изгибаемых изделий с покрытием в контактном слое возникают значительные сдвигающие напряжения. Они распределены по длине образца неравномерно и имеют максимальные значения на краях. Для того, чтобы обеспечить совместную работу элемента и покрытия, целесообразно снизить сдвигающие напряжения на краях слоя. Добиться этого можно, изменяя конструкцию соединения и свойств прослойки. Известно, что усилия на непрерывные связи соединительного слоя, работающие на сдвиг, передаются неравномерно. Перенапряженными являются крайние участки, где возникает опасность разрушения. Устранить это обстоятельство можно путем усложнения конструкции соединения (геометрии и деформативных свойств связей). При рассмотрении образцов с покрытием имеем случай прикрепления упругой пластинки постоянного сечения к жесткому основанию через связующие прослойки (рис.1). Напряжения в прослойке являются функциями координат т = t(z) и с = a(x). Предполагая, что для достижения цели может потребоваться изменение по сечению толщины прослойки, зададим h=h(x). Рис. 1. Расчетная схема балки с покрытием. При использовании безразмерных координат q = z/l и ? = х/l, формула для определения напряжений в конкретной точке, удаленной от начала координат на расстоянии x от ненагруженного конца, имеет вид c^=^T(Z>iz = 'i^^iz = T0-s^^Aq- (6) Учитывая, что т0 - касательные напряжения в начале координат, записываем данную формулу в виде ^ = то£т (7) гдеЛ?) = Jy^. 0То Относительные продольные деформации пластинки с модулем упругости Е определяются как г = Е(О=^ или с учетом преобразований £ = г> При рассмотрении сдвиговой деформации соединительной прослойки, учитывая линейные и угловые приращения размеров составных частей соединения, при изменении величин напряжений da (рис. 2) имеем dx + ^dx = dx + (h — dh^ty + dy) — hy, откуда ^dx = d(hy)и далее _ Adx _ d(hy) dx dx . Рис. 2. Схема деформационного состояния соединительной прослойки. Угловую деформацию прослойки γ, входящую в эти формулы, выраженную через касательные напряжения т = т (x) и модуль сдвига прослойки G = G(x) представим в виде т х отношения У = ~ как у=!0^^0, (11) Г Go т0 Gx’ где G0- модуль прослойки при х=0. Подставляя выраже ние (11) в формулу (10), получаем .^.GA £ G0 dx\ х т0 Gx) или после замены п еременных г^.^.^.Н.^Х (12) Go I d^ ho То G^ После приравнива ния правых частей (9) и (12) получаем дифференциальное уравнение d hi Tl Gi\ = G. L Lk^ d$\h0'т0'Gj E'8'ho} Интегрирование да ет ht T^ G0 _ G0 I I h т = Г X h F(^) + C’ (13) ho To G^ E о ho где F. При ^ = 0 будем и меть — • — •—= 1. ОтсюдаС = 1 — — ■ - ■ — F(0). ho To G^ e 6 ho ' Окончательно имее м h^■GO= ?{1+G0■^•г[F(^) — F(O)]}. (14) ho G^ Tt E 6 ho Полагая, что — =1, т.е. рассматривая случай равномерного распределения То передаваемой нагрузки, и еем J(T) = yid^ = ^. (15) Отношение---определяет характер распределения напряжений сдвига т(/)по длине ^0 прослойки. Следовательно, данное отношение можно заменить функцией/ (<;). Задавшись целью выровняться напряжения сдвига в зоне контакта слоев, зададим f2 функцию/(<;) = 1.В этом случае: J(^) = ^;F(^) = —;F(0) = 0. Тогда закон изменения толщины и характеристики прослойки запишется как ^.^0 = 1+^0. ±^±<2 h0 G; 2Е Ь8 h0S Реализация подобного решения возможна исходя из технологических условий и условий эксплуатации, а также за счет изменения толщины прослойки и ее деформационных свойств. ПриG0 = 1, характер изменения толщины прослойки определяется формулой Gf г^мф+т'/тН. (17) Hq L Е DO hq J Рисунок 3 дает представление о характере изменения толщины соединительной прослойки при постоянном модуле сдвига и различных значениях отношения длины элемента к начальной толщине прослойки l/h 0. Изменения толщины промежуточного слоя можно достичь, варьируя глубину проникания композита при нанесении покрытия.Если же решение реализуется за счет изменения свойств соединительной прослойки, то мы имеем h; — =1 и характер изменения деформационных параметров будет определятьсяпо формуле ho - = -М1+--Г-<21- (18) G; КО Е 8 ho Рис. 3. Характер изменения толщины промежуточного слоя при G=const и соотношениях длины элемента к начальной толщине прослойки l/h0: линия1- l/h о= 1; линия 2 - l/h о = 2; линия 3- l/h о = 5, линия 4 - l/h о = 10. Рис. 4. Характер изменения модуля сдвига промежуточного слоя при h=const и соотношениях длины элемента к начальной толщине прослойки l/h0: линия1- l/h о= 1; линия 2 - l/h о = 2; линия 3- l/h о = 5, линия 4 - l/h о = 10. На рисунке 4 показано изменение модуля сдвига прослойки при постоянстве ее толщины h и для разных величин отношенияl/ h 0. При рассмотрении обоих случаев принимались следующие соотношения параметров промежуточного слоя: 7 = 10, — = 0,4. 8 ’ Е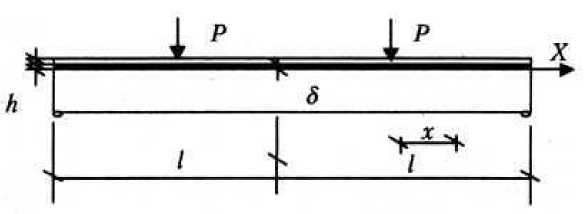
Список литературы Создание градиентных покрытий с комплексом свойств, обеспечивающих стойкость к эксплуатационным воздействиям
- Селяев В. П., Карташов В. А., Клементьев В. Д., Лазарев А. Л. Функционально-градиентные композиционные строительные материалы и конструкции. -Саранск: Изд-во Мордов. ун-та, 2005. -160 с. EDN: RUUHDR
- Победря Б. Е. Механика композиционных материалов. -М.: Изд-во Моск. ун-та, 1984. -336 с. EDN: IGETXE
- Какурин И. Р., Киселев А. Н., Лазарев А. Л., Шорин М. А. Практическое применение методов проектирования характеристик элементов на основе функционально-градиентных композиционных материалов //Огарев-online. Раздел «Технические науки». -2014. -С2(40) - С. 9. EDN: THVPMF
- Ржаницын А. Р. Строительная механика. -М.: Высш. шк., 1991. -440 с.


