Создание и фокусировка векторного пучка второго порядка с помощью субволнового оптического элемента

Исследование и создание новых материалов является актуальной задачей в промышленности, медицине и других сферах жизни [1 –3]. Одно из направлений исследований – это искусственные конструкции простой формы размером несколько нанометров [4], на основе которых создаются плоские или трехмерные конструкции с новыми свойствами. Метаматериалы также могут использоваться для управления излучением как один из способов управления параметрами света [5–7]. Интересным фактом является то, что показатель преломления может принимать отрицательные значения, что можно использовать для компенсации хроматических искажений [8, 9]. Также ранее были продемонстрированы метаматериалы для управления прозрачностью и преобразованием частоты [10].

При всех своих интересных свойствах метаматериалы сложны в производстве: они имеют высокое поглощение в видимой области спектра [11]. Поэтому часто используется класс оптических метаматериалов субволновой толщины, известный как метаповерхности [12, 13], которые можно рассматривать как оптические устройства [14– 16].

Среди оптических устройств особое внимание следует уделить аксикону. Изначально аксикон был известен в виде стеклянного конуса, формирующего протяжённое вдоль оптической оси изображение [17], однако в дальнейшем были созданы иные модификации, в том числе узкие микроаксиконы (конические волоконные зонды) [18, 19], градиентные аксиконы

[20, 21], логарифмические аксиконы [22], аксиконы с нелинейным профилем [23, 24], а также дифракционные аналоги [25, 26]. На текущий момент известно широкое применение аксиконов для острой фокусировки лазерного излучения [27–33], в том числе с целью усиления продольной компоненты электрического поля [34–37], которая важна в таких приложениях, как микроскопия, высокоразрешающая метрология, ускорение электронов и обработка материалов [38].

Цилиндрические векторные пучки представляют интерес для ряда областей оптики [39–42], среди которых можно отметить мультиплексирование данных в оптической связи [43] и амплитуднополяризационную модуляцию фокального распределения [44], что важно для оптического захвата, микроскопии, лазерной абляции [45]. Также ранее было показано [46, 47], что обратный поток энергии может быть получен путем острой фокусировки радиально-поляризованных лазерных пучков более высокого порядка. Существует ряд приложений, основанных на явлениях обратного потока энергии [48, 49], среди которых следует отметить острую фокусировку оптических вихрей [51], а также оптический захват и манипулирование [52].

В данной работе нами исследуются субволновые аксиконы, применяемые для создания и фокусировки векторных цилиндрических пучков второго порядка. Численное моделирование для подобных оптических элементов часто осуществляется методом конечных разностей во временной области (FDTD) [53] или методом конечных элементов [54]. В данном случае мы выбрали метод конечных элементов и Comsol Multiphysics в качестве программы, реализующей данный метод [55]. Показано различие получаемых распределений плотности потока мощности при различных углах закрутки спирали аксикона.

1. Субволновые решетки для формирования векторных пучков

Настоящая статья продолжает исследования, начатые в статьях [56, 57]. Известно [58, 59], что бинарная субволновая решетка может быть представлена как одноосный кристалл. Быстрая ось кристалла перпендикулярна канавкам решетки, а медленная ось ориентирована вдоль канавок решетки. Таким образом, полуволновая и четвертьволновая пластинки могут быть изготовлены в виде субволновых решеток определенной высоты. Матрица Джонса полуволновой пластинки в собственной системе координат (ось x ориентирована как быстрая ось) имеет следующий вид.

где ( r , ф ) - цилиндрические координаты, A ( r ) - амплитуда.

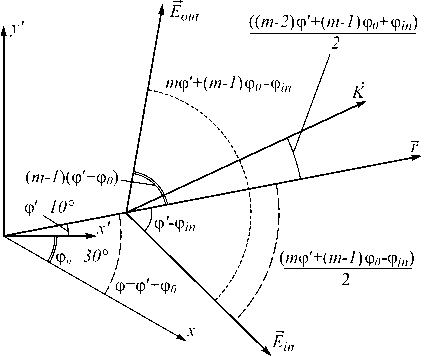
Рис. 1. Взаимное расположение координатных осей, электрических векторов и вектора субволновой решётки

eigen

M X /2 =

-1

Поворачивая систему координат на угол ф о , получаем новую систему координат ( r , ф' ), где ф’ = ф - ф ₀. В новой системе координат электрический вектор принимает следующий вид:

Если систему координат повернуть на угол относительно поляризационной пластинки, то матрица Джонса полуволновой пластинки примет вид:

M _ш = M rot M ^M rot =

cos ф - sin ф][ 1 0 V cos ф sin ф sinф cosф J|0 —1J(—sinФ cosФ cos2ф sin2ф sin2ф - cos2фJ

Е out

= E mad ( r , ф ') = A

^{( r} )

cos ( m - 1 )( ф ' +ф о ) sin ( m - 1 )( ф ' + ф ₀ )

Заметим, что азимутально поляризованный пучок m -го порядка имеет выражение:

Е out

= E m ( r , ф ) = A ( r )

sin ( m - 1 ) ф - cos ( m - 1 ) ф

Рассмотрим вектор электрической индукции E :

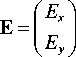
Если электрический вектор ориентирован вдоль оси x ( E y =0), матрица Джонса работает как матрица вращения, которая поворачивает электрический вектор на угол 2 ф . Используя этот факт, мы можем сконструировать субволновую решетку с изогнутыми канавками, которая создает цилиндрический векторный пучок произвольного порядка [56, 57]. Как было показано ранее [51], обратный поток энергии генерируется вблизи оптической оси при фокусировке радиального векторного пучка второго порядка.

Электрический вектор радиально поляризованного векторного пучка m -го порядка в цилиндрической системе координат имеет [54] следующий вид (рис. 1):

, ,. г cos mm - л ф]

E out = E mad ( r , ф ) = A ( r ) ( ’ , (4) I sin ( m - 1 ) ф I

Таким образом, поворачивая радиально поляризованный пучок на угол π / [2( m – 1)], можно получить азимутальную поляризацию. Интересный случай – это первый порядок поляризации. Когда m = 1, мы не можем получить радиальную поляризацию из азимутальной и наоборот.

Если угол между осью x' и начальным вектором электрического поля Е _п равен ф ,„ (как на рис. 1), то вектор субволновой решетки K в цилиндрической системе координат равен:

K (r, ф ‘) = 2п

Г ( m - 2 ) ф ' + ( m - 1 ) ф0 +ф ,„ ]^ cos

I ² J

. Г ( m - 2 ) ф ' + ( m - 1 ) ф0 +ф n ] sin

I 2 I

а в декартовой системе координат:

K ( x ', y ' ) = 2 П

Г m ф ' + ( m - 1 ) ф 0 +ф n cos

I 2

. Г m ф ' + ( m - 1 ) ф 0 +ф _/я sin

I 2

, (7)

Из уравнений (7), (8) мы можем заключить, что, изменяя значение (( m – 1) φ 0 + φ in )) / 2, мы просто поворачиваем элемент. В данной работе мы рассматриваем второй порядок радиальной поляризации и субволновую решетку для создания радиально поляризованного пучка второго порядка (когда m =2). Этот случай важен, потому что для различных значений (φ 0 + φ in ) /2 элемент имеет свою уникальную форму и не может быть получен один из другого с помощью вращения, как для других значений m . Ось x' определяет ориентацию элемента, а x определяет ориентацию оси поперечного сечения созданного пучка.

Если член (φ 0 + φ in ) /2 равен π /2, металинза для создания пучка (4) имеет быструю и медленную оси, как показано на рис. 2.

Рис. 2. Быстрые (серые линии) и медленные (чёрные линии) оси субволновой решётки, преобразующей линейно поляризованный пучок в радиально поляризованный пучок второго порядка, если (φ0 + φin) / 2, равен π / 2

• 2.    Уравнения медленных осей субволновой решетки

Исключим d из обоих уравнений (11), получаем:

Гф о+ ф, ) ^{1 f} _ _sin Г ^фо^+ф ,п М -о      (12)

cos                       sin — U.         ( 1Z, )

V 2 J r дф V 2 У д r

Данное уравнение можно переписать в следующем виде:

а ( r , ф ) ■v f — о,                                   (13)

Т.е. скалярное произведение некоторого векторного поля на градиент функции равно 0 в каждой точке поля. Следовательно, два этих вектора перпендикулярны в каждой точке. Исходя из того, что градиент перпендикулярен только гиперлиниям уровня функции, то векторное поле й ( r , ф ) состоит из векторов, касательных к гиперлиниям уровня функции. Очевидно, касательная к гиперлиниям в одной точке одна только в двумерном случае, но их бесконечно много в случае трехмерного и более многомерного пространства. В силу непрерывности вектора й ( r , ф ) (за исключением точки 0) можно положить, что данный вектор задает линии тока, которые скользят вдоль гиперлиний уровня. Запишем уравнения линий тока вдоль вектора а ( r , ф ) в параметрической форме:

r ‘ ( t ) — Са₁ ф‘ ( t ) — Са 2

д r _ _г Са^

д t

Рассмотрим более общий случай, когда член (φ 0 + φ in ) /2 принимает произвольное значение. В этом случае вектор субволновой решетки принимает следующий вид:

K ( r , ф ' ) = 2 П

^Г ( ф о + ф ,п Y cos I------------I

dr   с Г¹

— С cos dt V d ф .

— — - С sin dt

ф о +ф ,п | 1

2 У r ф о +ф ,п )

• Г фо + ф _/я sin I

Таким образом, вектор субволновой решетки зависит только от начальных углов и не зависит от азимутального угла. Фазовая функция субволновой решетки / ( x , у ) может быть получена из предположения:

V f ( r , ф ) = K —

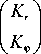
I f ) д г

1 f

_V r дф у

Приравнивая (9) и (10), можно вывести уравнение для фазовой функции / ( x , у ):

где С – некоторая константа. Решаем систему (14), избавляясь от dt .

rd ф

^Г ф о +ф ,п cos

V 2

dr

^, _sin I ф о +ф ,п I

Г фо + фп )

d ф tan I---------I —

V 2 У

ф tan

ф о +ф п

— - ln r + C .

Получаем первый интеграл, который задает семейство линий тока вдоль векторного поля а ( r , ф ) , если приравнять этот интеграл константе:

^ —ф tan ( ( ф _о +ф , _п )/2 ) + ln r . (16)

• д f  2 п    Г ф о + ф ,„ )

= cos II

• д rd  V 2 J

• 1 д f   2 п . Г ф о + ф ,п

  --= —sin I -------

• r дф d V 2

Тогда решение уравнения (12) будет произвольной функцией Ф , зависящей от конструкции V :

f ( r , ф ) — ф| ф tan V ^{ф о} "2 ^{ф ,} n J + ln r

Эквипотенциальные поверхности функции / ( r , ф ) служат одновременно медленными осями, а также гребнями решетки. Для поиска эквипотенциальных поверхностей нужно приравнять (16) константе. Имеем:

f (r,ф) = TI фtanI фо + фin J + lnr I.

( Ф0 + Фin 1

ф tan ------- + ln r = T .

V 2 J

Чтобы выполнялось условие (17) зависимости от определенной структуры, положим, что:

I ( фо + Ф,»

r = exp I T - ф tan I---2---

Уравнение (19) является уравнением спирали. Также (19) является уравнением медленных осей субволновой решетки, а также гребней решетки. Осталось определить значения константы T , которые определяют период субволновой решетки. Для этого нужно определить норму вектора субволновой решетки, используя формулу (10):

		( ^ f 1		( дТ 1
V f ( r , ф ) = K =	( K - 1 =	д r	= дФ	д r	=
	V K ф J	1 дС	= дТ	1 дТ
		V r дф j		V r дф >

(     1     1дФ r

дТ 1   Гфо +ф ,„ 1

— tan I---------- I

Vr V 2 /J

дФ 1

x

дТ I фо + фin 1

r cos ^{0 in}

I 2 J

x

I   ( фо + фin 11

cos

I 2 J

■ ( фо + ф«

sin 0 in

I 2

= Q ¹

r

(   ( фо + фin Ц cos

I 2 J

• I фо + ф in

sin 0 in

I 2

,

где

Q =

дФ

cos | фо +ф" 1 дТ

.

При этом, исходя из (9) и (11), можно заключить, что период будет равен:

d

2п

= —cos д f

фо + ф in

д r

2п    (фо + фй cos

дФ 1 | 2

дТ r

2п r   ( фо + фй cos

дФ | 2

дТ

Если требуется выставить наперед заданный период d 0 , то можно выразить:

дФ 2п r (фо + ф„ ---=---cos ------- дТ   d о    | 2

Таким образом, чтобы период d 0 был константным для заданного выбранного значения радиуса , дФ / дТ тоже должно быть равно константе: дФ / дТ = T . Тогда формула (17) примет вид:

T дФ дТ

^{2 n} r const d 0

( фо +ф« cos

I 2

Ясно, что радиус r const берется константным, иначе не выполняется (17), но это нам и надо, т.к. в кольце фокусирующего аксикона период не сильно (линейно) зависит от радиуса. Речь о фокусирующей фазе аксикона пойдет в следующем параграфе.

Отметим, что также необходимо, чтобы при обходе азимутального угла ф , от о до 2 л , чтобы быть непрерывной, функция / ( r , ф ) должна изменяться на величину, кратную 2 л . Это можно сделать, если положить, что T = N /tan( ф ₀ + ф in /2). Тогда не каждое соотношение r const и d 0 будет удовлетворять условию:

T =

^{2 п} r const      ^{( ф} о ^{+ ф} in ¹

cos

d о I 2 J

N tan ((фо +ф in )/2)

Решаем это уравнение, найдем N и округлим:

N = round I ²ⁿ r ns sin | ^{ф о +ф п 11} .

V d о V 2 J J

Далее определяем приблизительно выбранный пользователем период для реализации в программе:

d

0 program

^{2 n} r const   • ^{( ф} 0 ^{+ ф} in ¹

sin .

N V 2 J

Найдем уравнения кромок субволновой решетки. Поскольку [58] высота рельефа субволновой решетки будет определяться по формуле:

h ( ^r ) = ~ (1 ⁺ sign ( ^sin ( f ( ^r ) ) ) ) .                      ⁽²⁹⁾

Уравнения кромок решетки будут удовлетворять уравнению:

f (r ) = nq,

где q – номер кривой кромки решетки.

Подставим (24), (25), (28) в (30), получим:

f (r,ф)= 2Пrconst cos((фо +ф,„)/2)x d0                                     (31)

х ( ф tan ( ( ф о +ф in )/2 ) + In r ) = n q .

Решаем:

² r const     ^(ф о ^+ф in ^{1 (} , ^(ф о ^+ф in ¹ I I—.»¹ „

-------cos I----------II ф tan I----------I + ln r I = q.d о     I 2 J V V 2 J J

. (фо +ф™                qdо          т (32)

ф tan I----— I + In r =---------_?--------_T = T const .

V 2 J                  (ф о +ф in 1

2 r const cos I---------- I

Получаем уравнение, где известны все параметры:

. Г фо +фи 1 I            qd0         гр т фtanl —----I + lnr —------------------v = Tconst. (33)

I 2    )                 (Ф о +Фш 1

2r const cos l----~---- I

Чтобы для некоторого заданного радиуса обойти всю цилиндрическую плоскость, необходимо, чтобы параметр T const пробежал с точностью до константы от 0 до 2 n tan ( ф о + Ф n /2). Из равенства T _const = 2 n tan ( ф _о + ф ,_n / 2) найдем количество кромок Q , которые нужно нарисовать:

-----Qd ------ — 2 „ tan [*+b

~        (Ф о + Ф п 1 I 2

2 r const cos I ---- 2---- I

⁽ . ( Ф о +Ф п 1 ¹ sin l-------------I

K ( r , Ф ' ) = d

.

- cos (20±2m

Q — I 4 n r const sin I ^{Ф о} 2 ^{ф ,}” ) I / d 0 .

Тогда система уравнений для фазовой функции по аналогии с (11) перепишется в виде:

L -^„Г Фо ⁺ Ф п ¹

sin

• д rd  I 2 J

• <                 z v                        (39)

^{1 d} f_ ²” J Ф о ⁺ Ф п 1

cos r дф d | 2 )

А уравнение (12) примет вид:

sin (*±Ф - 1 1 f + cos (ф+ф п ) ^L — о.     (4о)

I 2 ) r дф | 2    ) д r

По аналогии с (16) получаем первый интеграл:

Здесь возможна проверка. Если период при обходе окружности по углу Ф равен:

7   ^4П rconst ^Ф= "О"

.

Очевидно, что d φ – это проекция d 0 на окружность:

d 0

“ Ф      / sin | Фо+Фи

Подставлением (28) в (36) убеждаемся, что получается (35) (учтем, что количество кромок в два раза больше количества штрихов решетки Q = 2 N ).

Шаг константы T const можно определить по формуле:

Step T _c

2 п tan ( Ф^ 1

I 2 J

Q

3. Быстрые оси решетки

Известно, что соседние зоны фокусирующей дифракционной линзы Френеля должны придавать падающему плоскому пучку разность фаз, равную π. Чтобы обеспечить такую разность фаз, мы будем располагать рассматриваемые субволновые решетки (суть полуволновые пластинки) в соседних кольцах фокусирующего аксикона таким образом, чтобы медленные оси субволновых решеток располагались под углом π /2. Если в одном кольце аксикона расположена решетка с гребнями (19), то в соседнем кольце гребни решетки должны быть им ортогональны. Найдем уравнения гребней решетки, ортогональных гребням (19). Эти же уравнения будут описывать быстрые оси субволновой решетки.

Итак, вектор решетки, перпендикулярный вектору (9), будет иметь вид:

w        +( ^ф о ^{+ ф} ,n 1 1

T — Ф cot ------- - In r .

I 2 )

Тогда решение уравнения (42) будет произвольной функцией Ф , зависящей от конструкции T :

f ( r , ф ) — Ф ( Т ) = ф|ф cot I ^{Ф о} + ^{Ф ,}” I- ln r I . (42)

Эквипотенциальные поверхности функции / ( r , ф ) служат быстрыми осями. Для поиска эквипотенциальных поверхностей нужно приравнять (43) константе. Имеем:

ф cot I ^Ф 2 ^{ф ,п} )- ln r — T .                         (43)

Выражаем r :

r — exp |ф cot I^ l +^ n )- t ^.                  (44)

Период решетки будет выражаться из (39) и (41) следующим образом:

^{2 n r} ■ d — —-— sin дФ

^ф о + ^ф ,n

дф

Если требуется выставить наперед заданный период d 0 , то:

дФ дТ

2 п r . --sin d ₀

фо + ф,n

По аналогии с предыдущим случаем будем полагать функцию Ф ( Т ) линейной, и (42) перепишется как / ( r , ф ) = T ( ф cot (( ф о + ф n ) / 2) - ln r ), где T const ⁼ дФ / дТ = - 2 п r const / d о sin (( ф о + ф ,n ) / 2). Ясно, что радиус r const берется константным, иначе не выполняется (42).

Также необходимо, чтобы при обходе угла ф от 0 до 2 п функция / ( r , ф ) изменялась на величину, кратную 2 п , иначе функция будет иметь разрыв. Непрерывность / ( r , ф ) можно обеспечить, если положить, что T const = - N /cot(( ф ₀ + ф in )/2). Тогда решая это уравнение, найдем N и округлим: N = round ((2 п r const /2) cos (( ф о + ф in )/2)). Далее определяем приблизительно выбранный пользователем период для реализации в программе:

d

0 program

rconst

N

Г ф0 + фin

I 2 .

аморфному кремнию при длине волны 633 нм. Окружающая среда – вакуум. Числовая апертура фокусирующего аксикона NA = 0,99. Числовая апертура рассчитывалась по стандартной формуле NA = λ / t , где λ – длина волны, t – период фокусирующего аксикона. Период фокусирующего аксикона t следует отличать от периода субволновой решетки d . Период фокусирующего аксикона t = λ / 0,99. Высота рельефа субволновой решетки выбрана равной 120 нм согласно исследованиям [50].

Аналогично предыдущему случаю можно заключить, что для заданного периода d 0 количество интервалов дробления будет:

Q =

Г ф о + ф in 4 п r_con st cos I —2— I d 0 program

Шаг константы T const будет определяться по формуле:

Step

T const

2п

. Г ф о + фш tan I — —

.

Q

• 4.    Особенности структуры субволнового аксикона

• 5.    Численное моделирование процесса

В формулах (19) и (44) есть особенность, которая возникает, если ( ф ₀ + ф in )/2 равно 0 или п/2. Этот случай соответствует субволновому аксикону и элементу типа «радиальная мира». Данные элементы теоретически и модельно рассмотрены в [57].

Также мы полагали, что период решетки не зависит от ф . Удобство данного упрощения состоит в том, что фокусирующий аксикон имеет кольцевую структуру, и в одном кольце желательно иметь приблизительно один и тот же радиус, что и обеспечивается независимостью от ф . В общем случае согласно формулам (22) и (45) период может зависеть от структуры V , взятой целиком. Ничто не мешает читателю рассмотреть этот случай.

На рис. 3 показана одна полоска субволновой решетки (22), когда tan(( ф ₀ + ф in )/2) = 0,05, т.е. когда угол между быстрой осью очень мал и равен ( ф 0 + ф in )/2 = 2,86.

На рис. 4 показаны быстрые (черные линии) и медленные (серые линии) оси субволновой решетки при tan(( ф ₀ +ф _in )/2 ) = V3 , рассчитанные по формулам (25) и (45).

Общий вид фокусирующего аксикона показан на рис. 5.

В данной работе проведено моделирование работы описанного аксикона в пакете Comsol. Показатель преломления вещества субволновой решетки был выбран 4,206 + 0,42174 i , что соответствует

Рис. 3. Субволновая решётка при tan (( p + p in ) /2) = 0,05

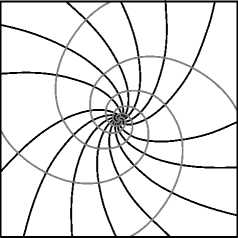
Рис. 4. Быстрые (чёрные линии) и медленные (серые линии) оси субволновой решётки при tan(( p ₀ + p in )/2) = V 3

Рис. 5. Общий вид аксикона при tan(( p ₀ + p in )/ 2 ) = V 3

Поляризующий аксикон освещается Гауссовым пучком, поляризация которого ориентирована вдоль оси х , то есть горизонтально по отношению к рис. 5.

Результаты моделирования работы предложенных аксиконов приведены на рис. 6, где показаны распределения продольной компоненты плотности потока мощности в продольном сечении xz (a), а также в по- перечном сечении xy на расстоянии 1,5λ от поверхности аксикона (в, д). Также на рис. 6б, г показаны распределения амплитуды электрического вектора в поперечном сечении xy. Углы закрутки аксикона (ϕ0 + ϕin) /2 выбраны равными 0,3π (б, в) и 0,4π (г, д). Элемент освещался Гауссовым пучком с плоским волновым фронтом.

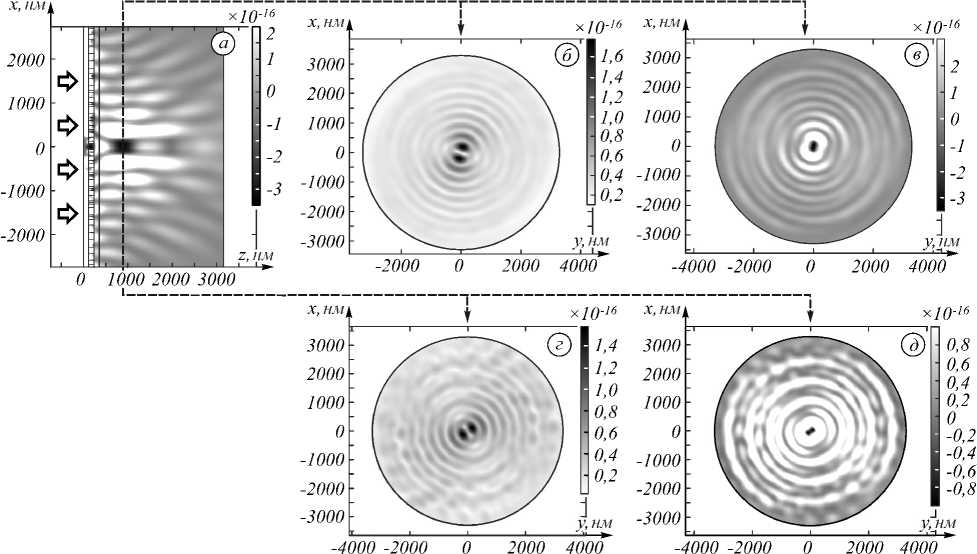
Рис. 6. Распределение продольной компоненты плотности потока мощности в продольном сечении xz (a), в поперечном сечении xy на расстоянии 1,5λ от поверхности аксикона (в, д), распределения амплитуды электрического вектора в поперечном сечении xy (б, г). Углы закрутки аксикона ( ϕ 0 + ϕ in ) / 2 выбраны равными 0,3π (б, в) и 0,4π (г, д)

Из рис. 6 в , д видно, что в центре распределения формируется область, в которой направление потока энергии направлено противоположно оптической оси элемента, то есть в сторону источника излучения, что согласуется с работой [51].

Так как числовая апертура высока (0,99), большая доля энергии сформированного пучка распространяется в направлении, перпендикулярном оптической оси. Так как падающий пучок имеет плоский волновой фронт, то вектор потока мощности падающего пучка сонаправлен с оптической осью z.

Оценим долю мощности падающего пучка, которая переходит в продольную компоненту. Интегрирование показывает, что падает на аксикон мощность P full =3,62×10 ^–26 Вт.

Трансформированную мощность оценим интегрированием продольной компоненты вектора Пойнтин-га по фокальной плоскости. Для ( ϕ 0 + ϕ in )/2=0,3 P z = 2,5×10 ^–27 Вт, т.е. 8% от падающей мощности, для ( ϕ 0 + ϕ in ) /2=0,4, P z = 2,3×10 ^–27 Вт, т.е. 7,5 % от падающей мощности.

Заключение

В этой статье выведены уравнения для вектора и кромок субволновой решетки поляризационного элемента, который создает радиально поляризованный пучок второго порядка. Показано, что элемент может быть выполнен с различной формой для разной ориентации входной и выходной поляризации. Может быть в форме оптического мира, кругового и скрученного аксикона.

Проведено численное моделирование формирования и фокусировки радиально поляризованного пучка второго порядка. Показано, что обратный поток энергии может возникать вблизи оптической оси элемента.

Приведены оценки дифракционной эффективности рассмотренных аксиконов, которые показали, что аксикон с углом закрутки 0,3π имеет дифракционную эффективность 0,04 %, а аксикон с углом закрутки 0,4π имеет дифракционную эффективность 0,02%.

Работа выполнена при поддержке средств финансирования Программы развития Самарского университета на 2021- 2030 годы в рамках программы «Приоритет-2030» в части «Введение» и Российского научного фонда (проект № 20-72-00051) в остальных частях.