Создание комплекса программных средств прогнозного моделирования динамики биогеохимических циклов в мелководном водоеме с учетом кислородного режима

Одной из основных задач современного научного сообщества является исследование и анализ биологических процессов и систем водной среды. В связи с активными климатическими и, как следствие, гидробиологическими изменениями, активно протекающими в течение последних десятилетий, происходит «перестроение» экологических со-

Создание комплекса программных средств прогнозного моделирования динамики ...

обществ. Особенно эти процессы влияют на водные экосистемы, структурно-видовую форму развития различных биологических сообществ под воздействием биотических и абиотических факторов.

Изучение особенностей и прогнозирование состояния водных экосистем является предметом многочисленных исследований многих отечественных и зарубежных ученых, научно-исследовательских групп, институтов и организаций. Весомый вклад в исследование гидробиологических процессов и водных экосистем внесли Г.И. Марчук, А.И. Сухи-нов, Г.Г. Матишов, В.Г. Ильичев, Ю.А. Домбровский, Ю.В. Тютюнов, Е.В. Якушев и др. Учеными крупных российских исследовательских центров и институтов в области океанологии, таких как Институт прикладной математики имени М.В. Келдыша, Институт вычислительной математики имени Г.И. Марчука РАН, Институт океанологии имени П.П. Ширшова РАН, проводятся многочисленные исследования, посвященные анализу и моделированию сложных экологических систем, прогнозированию ряда климатических изменений, протекающих в Мировом океане. Научными сотрудниками и учеными Всероссийского научно-исследовательского института рыбного хозяйства и океанографии (ВНИРО) и его филиалов проводятся многочисленные комплексные научные и исследовательские работы в акватории рыбохозяйственных бассейнов России и Мирового океана, включающие мероприятия по разработке обоснований общих объемов допустимых уловов и объема рекомендованного вылова водных биоресурсов на основе создания инновационных решений в области развития аквакультуры, молекулярной биологии, генетики, по комплексной оценке факторов влияния на водные биоресурсы, а также определение тенденций экономической политики в рыбохозяйственной отрасли нашей страны. Научными сотрудниками Центра системы мониторинга рыболовства и связи решаются задачи обеспечения мониторинга и определения путей поддержания устойчивого развития биологических ресурсов водных объектов на государственном уровне, мониторинга и обеспечения контроля за промышленной деятельностью судов рыбопромыслового флота.

Среди выдающихся ученых, внесших большой вклад в изучение гидрологии и океанологии, также следует отметить В.П. Дымникова, занимающегося исследованием климата и океанологии, моделированием атмосферы и океана; А.С. Монина и М.Ю. Белевича, исследующих процессы кинематики водной среды, турбулентности и микроструктуры океана. Известным советским ученым А.С. Судольским проведен ряд важных исследований в области изучения динамики вод и прибрежных процессов в водных объектах различной гидрологической сложности, позволяющих разрабатывать эффективные решения задач в области проектирования, строительства и эксплуатации сложных гидротехнических сооружений, а также в области разработки концепций условий оптимального хозяйственного природопользования водоемов [1].

К передовым зарубежным научно-исследовательским организациям и институтам, специализирующимся на всесторонних фундаментальных, мультидисциплинарных исследованиях в области экологических процессов водных систем и восстановления окружающей водной среды, относятся Yantai Institute of Coastal Zone Research, Chinese Academy of Sciences (VICE, CASE, Китай), Centre for Water Research of National University of Singapore (CWR of NUS, Сингапур), Korea Institute of Ocean Science and Technology (KIOST, Корея), Swedish Meteorological and Hydrological Institute (SMHI, Швеция), National Oceanic and Atmospheric Administration (NOAA, США), UK Centre for Ecology and Hydrology (UKCEH, Великобритания), в область компетенций которых также входит разработка информационных комплексов и систем, позволяющих осуществлять мониторинг и прогноз экологической обстановки водных систем.

К одним из важных факторов устойчивого развития водных экосистем, в особенности мелководным, относятся газообменные процессы населяющих сообществ флоры и фауны с окружающей средой, жизненно важным из которых является дыхание. На сегодняшний день в мелководных акваториях широко распространено явление кислородного минимума (oxygen minimum zones, OMZ). OMZ-зоны возникают прежде всего в высокопродуктивных районах с ограниченной вертикальной циркуляцией водных масс. В последние годы в мелководных водоемах наблюдается тенденция к активизации заморных явлений и процессов, а также активное образование зон аноксии и гипоксии, которые возникают вследствие антропогенного воздействия (строительство различных гидротехнических сооружений, проведение дноуглубительных работ, эвтрофикация, глобальные климатические изменения). По мере развития кислород-дефицитных зон водоема происходят негативные перестройки гидробиологических сообществ в сторону доминирования организмов с анаэробным метаболизмом [2]. При понижении уровня содержания кислорода полностью исчезают донные животные и появляются группы бактерий, жизнеспособные за счет разложения органических веществ, образованных фитопланктонными популяциями в результате поступления с суши различных удобрений, сбросов сельскохозяйственных стоков и др., а также реакции восстановления сульфата. При этом образуется сероводород, который для большинства организмов является ядовитым и быстро окисляется при наличии кислорода [3].

Существующие методы и средства прогнозного моделирования динамики гидробиологических процессов водной среды с учетом биотических и абиотических факторов, включая процессы распределения кислорода, углекислого газа и солей, основываются на общих научных подходах, упрощенных математических моделях, отличающихся низкой адаптивностью, отсутствием возможности моделирования нелинейных динамических процессов, свойственных большинству водных экосистем, некорректным заданием границ расчетной области, основанных на достаточно грубых аппроксимациях относительно реальной гидрофизики водоема. Универсальные пакеты программ (например, Mars3d; программный комплекс CHARISMA; «Экоинтегратор»; комплекс SALMO; комплекс программ CHTDM; CARDINAL и др.) интегрируют ограниченный набор достаточно общих моделей, алгоритмов и методов моделирования, которые не могут быть реализованы для других мелководных и прибрежных экосистем. В связи с этим возникает необходимость в разработке комплекса алгоритмических и программных средств, позволяющих на основе усовершенствованных математических моделей биогеохимических циклов и эффективных численных методов осуществлять прогнозное моделирование на высокопроизводительных вычислительных комплексах.

Кислород – основной механизм формирования биологической активности в водоеме

Исследование гидробиологических процессов и трофических взаимодействий мелководных водоемов направлено на изучение продукционно-деструкционных процессов гидробионтов, связанных с трансформацией вещества и энергии в экосистемах. Важное значение имеют химические превращения веществ, опосредованные взаимодействия, включая действие продуктов жизнедеятельности планктонных, рыбных популяций.

Известно, что биологические и термодинамические процессы, протекающие в мелководном водоеме, активная реакция среды (pH) и другие факторы оказывают непосред-

Создание комплекса программных средств прогнозного моделирования динамики ...

ственное влияние на газовый режим водной экосистемы. Газораспределение в толще водоема имеет довольно сложный характер, который зависит от гидродинамических и географических особенностей водоема и интенсивности протекающих в нем биологических процессов [4].

Основным механизмом формирования биологической активности в водоеме является кислород ( O₂ ). Зачастую кислород представляет собой лимитирующий фактор водной среды как для первичной, так и для вторичной его продукции. В результате турбулентной и молекулярной диффузии атмосферный кислород поступает в водоем. Количество кислорода напрямую зависит от температуры, солености, а также ветровых воздействий и течений. Инвазия кислорода происходит через поверхность воды, поэтому наиболее насыщенной кислородом зоной является зона фотосинтеза, расположенная в верхнем слое водной толщи. Подавляющее количество организмов получают энергию для своей жизнедеятельности в ходе окисления органических веществ, обеспечивающего также деструкцию веществ мертвых организмов.

Когда уровень растворенного в воде кислорода достигает максимума, происходит его выход на границе раздела сред при контакте с воздухом. Этот процесс протекает особенно интенсивно при увеличении температуры. В основном объем кислорода идет на дыхание преимущественно бактерий, которые расходуют порядка 90 % от его общего объема; часть кислорода расходуется на процессы окисления различных минеральных и органических соединений.

Кислородный режим водной среды зависит от ее аэрации и абсорбции. Потребление кислорода на процессы окисления, дыхания осуществляется во всем объеме водной толщи, включая дно. Поэтому дефицит кислорода особенно выражен в водоемах с интенсивными деструкционными процессами.

В то же время без углекислого газа также невозможно существование жизни в водоеме. На Рисунке 1 схематично представлена взаимосвязь углекислого газа ( CO₂ ) и кислорода в водной среде ( H₂O ).

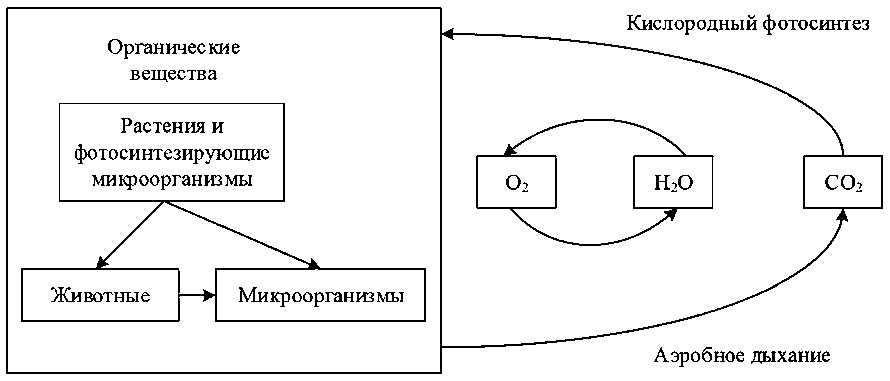
Рисунок 1. Биологический круговорот углерода и кислорода в водной среде Источник : составлено авторами.

К факторам поступления и накопления углекислого газа в водной толще относятся попадание различных химических соединений (в особенности угольной кислоты) и проте- кание геохимических процессов (например, разрушение осадочных пород), дыхание гидробионтов, процессы диффузии O2 из атмосферы. Концентрация диоксида углерода в водоеме снижается благодаря фотосинтезирующим организмам, его потребляющим, а также в результате связывания в соли угольной кислоты.

Известно, что скорость поступления кислорода из воздушной среды зависит от солености, температуры, уровня кислородного насыщения, турбулентности поверхности раздела сред «вода – воздух». Перенос кислорода через поверхность «вода – воздух» осуществляется под действием градиента концентрации. Скорость распространения O₂ определяется как отношение данной концентрации растворенного в воде кислорода к значению концентрации насыщения. Градиент концентрации математически выражается следующим образом:

A Ct = Cs - Ct, где Ct – значение концентрации кислорода в момент времени t ; Cs – значение концентрации O2 при 100-процентном насыщении; A Ct - значение градиента концентрации в момент времени t .

Скорость распространения растворенного в воде кислорода увеличивается с ростом градиента концентрации, следовательно, при приближении уровня содержания O₂ к показателю 100%-процентного насыщения скорость распространения уменьшается. По этой причине намного сложнее полностью обогатить водную среду кислородом, чем повысить его концентрацию на 1…2 мг/л.

Перенос кислорода описывается следующим образом:

A C/ A t = KA (Cs - Ct), где K – константа, которая учитывает влияние процесса турбулентности и зависит от условий; AC]At - изменение значения концентрации растворенного в воде кислорода за время At; A - площадь поверхности контакта раздела сред «вода - воздух».

Данное выражение показывает, что скорость изменения показателя концентрации кислорода A C] A t определяется произведением константы K с учетом процессов турбулентности, протекающих на границе раздела сред «вода – воздух», на площадь поверхности контакта и, соответственно, значение градиента концентрации C_s – C_t .

Проведение исследований

В данной работе моделирование гидробиохимических процессов в мелководных водоемах проводилось для акватории Азовского моря как наиболее крупного представителя мелководной системы юга России, обладающего рядом специфических особенностей (небольшая глубина, значительный перепад солености, большой речной сток, почти равномерный прогрев водной толщи) и претерпевающего выраженные гидрологические изменения ввиду климатической и антропогенной нагрузки.

Моделирование проводилось на основе разработанной модели процессов самоочищения с учетом кислород-дефицитных условий в придонных слоях рассматриваемого моря:

Создание комплекса программных средств прогнозного моделирования динамики ...

д q   д q   д q          д q         д f д q )

+u-^i-+v-^ + w - w    '- = Д Aq +v+ д t     дx    дy         g ’ д z    '      дz I ' дzJ

• ^V 1 = g 1 ( ^q 1 , q 3 , q 8 , q 9 ^)- Л ⁽ q 11 ) q 1 ’ ^V 2 = g 2 ⁽ q 2 , q 4 , q 10 ) ^- ^ 2 q 2 ,

• ^V 3 = ^Y 3 « 2 ⁽ q 4 ) q 2 q 3 ^- g 3 ^{( q} 1 , q 3 ^)- A q 3 ⁺ B ^{( q} 3 ^- q 3 ^{) + f} ,

• V 4 = 21 q1 + 2-2 q 2 + Л5 q 5 - g 4 ( q 2, q 4, q 5 ), Щ5 = g 5 ( q 4, q 5, q 8 )- Л5 q 5,

^V 6 = ( g 6 ⁽ q 4 , q 8 ^{)- 2} 6 ) q 6 , ^V 7 = g 7 ⁽ q 6 ^{)- 2} 7 q 7 ’ ^V 8 = ( g 8 ⁽ q 2 , q 7 ^)- Л ) q 8 - ^Y 8 « 1 ⁽ q 8 ) ^q 1 ,

• ^V 9 = g 9 ⁽ q 1 ^{)- 2} 9 q 9 ’ ^V 10 = g 10 ⁽ q 1 , q 10 ^{) + Y} 2 « 2 ^{( q} 10 ) ^q 2 ^-( ° "1 q 1 ^{+ Y} 7 ^q 7 ) ^q 10 ,

• ^V 11 = g 11 ^{( q} 1 , ^q 11 ^{) — 2} 11 ^q 1 ,

где U = ( u , v , w ) - вектор скорости водного по тока; w g - скорость гравитационного осаждения 1 -й компоненты, если она находится во взвешенном состоянии; A - двумерный оператор Лапласа; ^ i , v i - коэффициенты турбулентного обмена соответственно по горизонтальному и вертикальному направлениям; V i - химико-биологический источник (сток) или член, описывающий процесс агрегирования (слипания-разлипания), если соответствующая компонента является взвесью, индекс i указывает на вид субстанции, 1 = 1,12 ; 1 - значение концентрации фитопланктона ( P ) ; 2 - аэробных тионовых бактерий Thiobacillus ( BT ); 3 – минерального питания (биогенные вещества: соединения азота, фосфора, кремния) ( M ) , 4 - детрита ( D ); 5 - анаэробных бактерий рода Desulfovibrio ( BD ); 6 - сероводорода ( H₂S ) ; 7 - элементарной серы ( S ) ; 8 - сульфатов ( SO ₄ ) ; 9 - метаболита фитопланктона ( МР ); 10 - растворенного кислорода ( О₂ ) ; 11 - зоопланктона (веслоногие рачки Copepoda ) ( Z ); 12 - углекислого газа ( CO₂ ) .

Процессы биогеохимических циклов химических элементов в кислород-дефицитных условиях были параметризованы при разработке данной математической модели.

Пусть « m ( q j ) = ^a m^ax q j / ( K ^ + q j ) , m = { l ^,2, 5,10 } , j = { 3 ^,4, 8 } , o « ( q j ) - значение скорости поглощения m -м гидробионтом j -го вещества, « m ^ax - максимально возможная скорость поглощения для m -го гидробионта (при высокой концентрации j- го питательного вещества), K_m ^j – константа полунасыщения m -го гидробионта j -м веществом;

g 1 (q1,q3,q8,q9 ) = (71a1 (q3 ) + Y8a1 (q8 ) + Y9q9 )^1 q1, g2 (q2,q4,q10 ) = ( Y2«2 (q4 ) + Y10«2 (q10 ))ф2q2, g 3 (q1, q 3 )=«1 (q 3) q1, g 4 (q 2, q 4, q 5 )=«2 (q 4) q 2+«4 (q 5) q 4, g 5 (q 4, q 5, q 8 )=ф5 («5 (q 4)+°5 q 8) q 5, g 6 (q 4, q 8 )=( y4 q 4+Y8 q 8) q 6, g 7 (q 6 ) = Y6 q 6 q 7 , g 8 (q 2,q 5,q 7 ) = ( Y2 q 2 - °5 q 5 + Y7 q 7 ) q 8, g 9 ( q1 ) = Y9 q1 ’ g 10 ( q1, q10 ) = Y10 q1 q10 > g 11 ( q1, q11 ) = Y11^11 q1 q11, f(x, y,z)

– функция источника загрязняющего вещества (ЗВ); B – удельная скорость поступления ЗВ; q3 - предельно возможная скорость поступления загрязняющего биогенного веще- ства; Xi, i £1,12, (i ^ 4) - коэффициенты, которые учитывают убыль бактерий, фито- и зоопланктона и веществ за счет элиминации (смертности), выедания представителями высших трофических уровней и разложения; yi, i £1,12, i ^{3,6,10,12} - передаточные коэффициенты трофических функций; у10 - коэффициент выделения кислорода фитопланктоном в процессе фотосинтеза; <71 - коэффициент потребления кислорода за счет дыхания фитопланктона; ст5 - коэффициент восстановления сульфата до сероводорода бактериями (BD) вследствие анаэробного дыхания.

Функциональные зависимости скорости роста фитопланктона и бактерий от значений температурного режима ( T ), уровня солености ( S ) (по Леману) и освещенности водной среды ( I ) (по Стилу) определяются следующие образом:

I Г                               ^{2                            2}            1

• ^ф т ⁽ T , ⁵ , 1 ) = | ^еХР } 1 ^{- a} m ( ( ^{T -} T opt ) [T opi ) ^- P m ( ( ^{5 -} S opt ) (S opt ) ^- I / I opt , m = { 1, ² , ⁵ , ^{11 }} , где I ( h ) = 1 ₀ e xp ( -9 h ) , h - глубина водоема; 9 - коэффициент затухания, который про

порционален концентрации взвешенных в воде веществ (детритаи фитопланктона); I0 – суммарная солнечная радиация на водной поверхности; где Sopt , Topt – соленость и температура, наиболее благоприятные для данного вида гидробионтов; ат > 0, вт > 0 - коэффициенты ширины интервала толерантности планктона и бактерий к показаниям температуры и солености водоема соответственно.

Расчетная область G – замкнутый бассейн, который ограничен невозмущенной по- верхностью водоема 20 , цилиндрической боковой поверхностью ст, донной поверхностью 2H = 2H (x, y), Е - кусочно-гладкая граница области G, Е = Е0 оЕH v>ct , 0 < t < T0.

Граничные условия:

dq, q, = 0 на ст, если U < 0; -= = 0 на ст, если U > 0;

* i            n d _d n                       n

^ ( q ) , i ф,4,6,7 } ;

dq ф = -£Al на 2h dz

. ^ q i- = ^ ( q i ) « ^{а 2} 0 , ^ ( q i ) =ф ( K i ^- q i ) , i = ¹⁰ ; d z                     к

i

0, ie{1,2,5,8,9,11}, где K10 – концентрация растворенного в воде кислорода при насыщении; a0 – коэффици- ент аэрации, si - коэффициент поглощения i -й субстанции донными отложениями, ^i - заданная функция, i = 1,12 . Начальные условия:

q i|_t = ₀ = q i 0⁽ x , y , z ), i = ^1,12.

На Рисунке 2 приведена структурная схема биологического цикла мелководного водоема.

Создание комплекса программных средств прогнозного моделирования динамики ...

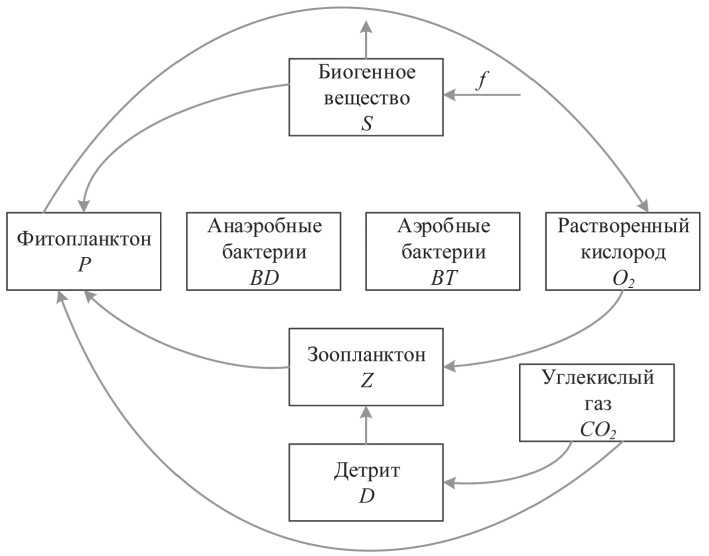
Рисунок 2. Схема модели биогеохимических циклов в мелководном водоеме Источник: составлено авторами.

В основе разработанной модели гидробиохимических циклов мелководного водоема (1)–(3), входящей в состав программных средств прогнозного моделирования, лежит система нестационарных уравнений переноса вещества, включающая нелинейные члены для описания движения водной среды, процессов микротурбулентной диффузии, разложения детрита в результате деятельности аэробных и анаэробных бактерий, гравитационного оседания взвешенных веществ и примесей. Нелинейность построенных функциональных зависимостей значений скорости роста фитопланктона и бактерий позволяет детально описывать продукционно-деструкционные процессы, протекающие во всей водной толще, а также осуществлять контроль их динамики при избыточном поступлении биогенных веществ (соединений фосфора, азота, кремния), соединений серы, включая сероводород и сульфаты, при различных показателях растворенного в воде кислорода, распределения детрита, показателей пространственно-временной изменчивости уровня освещенности, солености, температурного режима водной среды, что отвечает современным представлениям о благоприятном функционировании гидробиоценоза.

В совокупности с перечисленными выше факторами для модели (1)–(3) в качестве входных данных использовались результаты расчетов по гидродинамической модели А.И. Сухинова, А.Е. Чистякова и др. [5], учитывающей ряд биотических факторов: сила Кориолиса, сложная форма прибрежной области, рельеф дна водоема, ветровая нагрузка, процессы испарения, трения о донную поверхность, выпадение осадков, стоки рек, водообмен с Черным морем, уровень солености, динамика температурного режима.

Функция трехмерного распределения кислорода для системы (1)–(3) имеет вид

C = C ₀ - k ₀ , C ( x , y , z , t ) = ϕ ( x , y , z , t ), ∀ ( x , y , z , t ) ∈∂ G , 00 _{h 0}

где C0 – значение концентрации кислорода при отсутствии органических примесей; k0 – объем кислорода, потребляемого при окислении детрита; h0 = const – область водной толщи около дна, заполненная максимальным количеством концентрации детрита; H – высота водного столба, максимальный размер расчетной области по вертикали, h0 << H.

Дискретизация предложенной в работе математической модели осуществляется на основе универсальной и широко применяемой равномерной прямоугольной сетки [6].

В данном случае возникает проблема погрешности решения подобных модельных задач гидробиологии на границе расчетной области, которая решается посредством применения метода частичной заполненности расчетных ячеек [7]. Поэтому при решении поставленной в данной работе задачи для описания сложной, пространственно неоднородной геометрии исследуемых объектов использовались коэффициенты q ₀ , q ₁ , q ₂ , q ₃ , q ₄ . Данные коэффициенты позволяют описывать степень заполненности прямоугольных ячеек и рассчитываются по следующим формулам:

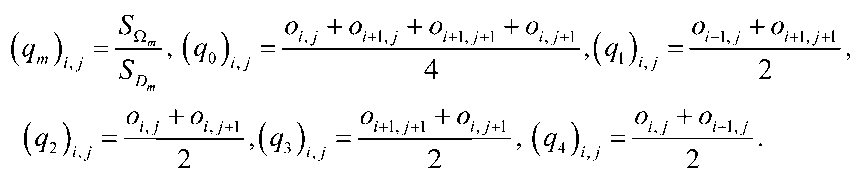
Использование разностных схем повышенного порядка точности для решения задач переноса позволяет сократить количество вычислительных узлов в два раза, что, однако, увеличивает время вычислений на каждом узле. Разработанные схемы повышенного порядка точности позволяют сократить погрешность аппроксимации в 5–30 раз для решения различных модельных задач и типов расчетных сеток. Традиционные разностные схемы не позволяют добиться подобной точности, несмотря на то, что в данном случае количество операций в расчетных узлах меньше [8].

В результате проведенных вычислений была выполнена дискретизация оператора конвективного переноса uc' повышенного (четвертого) порядка точности для численной ре-

ализации задачи (1)–(3):

( q« ) L ( c ) = ( q, ) u '/ т ^ г²² c. ₂ + ⁰ Л C V 7        /ⁱ 12 h ( q 0 )      ^{i +2}

(

—I

V

u i + 1/2

(q1 )<12Г

( ^q1 ) _i ⁺ ( q о ) i

+

+ ( q ) u ti/² ( S1L 2^Л 12 h ( q о ) _i

u + 1/2 + k ,^{( 1 )} + k ,^{( 2 )} I

2 h       ^{i i} )

7 7

r

/   \ ui + 1/2

^{( q} 1

V

⁽ q ² ) i + 1

( q 0 ) + 1 J

—

— ( q 2 ) ^Ui — ^{1/2 2 i} 12 h

L( q1L1 V 2 + ( q0 ) i-1 J

+ ( q 2) ^Ui — ^{1/2 ( 42 } i} 2 h

—

( q) u i ¹/² + ^{( 41 ) i} 2 h

c i ⁺      (4)

J

+

—

( q ). u ^{1 2 1}/² T q ²) ¹ -+ ( q 2 ). u i — ^1/2

^{V 1Л} 12 h ( q ₀ ) _i ^{V Л} 12 h

—

⁽ q 2 ) i

2+(q2)i        1

2 + T^ +(q2 )i ( q 0 ) i J ui—1/2 ( q2 )i—1 c

^{12 h} ( q 0 LЛ ²

— u i — / ²- + k ,⁽² ) — k ,⁽¹ )

2 h ⁱⁱ

c i — 1 ^—

ki <-)=

T q ¹^^ ( ^ui + 1 ^— u i , ) ^—v q ²^¹ ( ^ui ^— u i — 1 ) / ( ^{8 h} ) , ^ki ^{(2 ) = (} q 0 ) i                  ⁽ q 0 ) i              J

⁽ q ¹ ) , ( ui + i

—

u i} , ⁽ q 2 ) i Г u i ^— u i — 1

( q 0 ) i V 8 h J ( q 0 ) i V 8 h

Создание комплекса программных средств прогнозного моделирования динамики ...

и диффузионного переноса (цс')' повышенного (четвертого) порядка погрешности аппроксимации:

⁽ q 0 ) Ld» ( c ) - — ⁽ q 1 ) * ^ q )

г         \ ^М* +1/2    -и U\ ^Ц +1 ^{f (} q ¹ ) *

c * ^{+ 2} ^ q ¹ )* h ² c * ^{+ 1 +(} q ¹ )* 12 h ² ^ ( q 0 ) *

А

+(q) M M—(q )f “"' “"+k ]J c+i-f( q) M '+(q) M+ V 2 Л 12h2 (q0) ЛI 12       * J J * V Л h2     2 i* h2

+

f( q 2)

(q1) * Mt    )

¹² h j ^q 0 ) ,

1 + 2

⁽ q ¹ ) ,

^{+ (} ’ 2 ^ [ ( q 0 ) .

i - 1

^{+ 2 +(} q 2 ) * J

f ЦкЦи

I 12

-

k

-

^{+( q} 1 ) *

-( q ).f Ц‘+1-Ц’- + k,11 c, +

¹⁷ * (     12         * JJ *

f

/   \ ^Ц* - 1/2

⁽ q ² ) * h ²    c * ^{- 1}

V

^ц * + 1 ^{( q 2} ) *

12 h ² ( q о ) *

^ц * + 1 ^{( q 2} ) * 12 h ² ( q о ) *

, / А Ц * - 1 ^f( q 2 ) * ⁺⁽ q ² ^H h ² L( q 0x

^{+ (} q 2 ) *

f M"- Ц1

V 12

^{+( q} 1 ) *

-

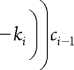
⁽ q 2 )

^ц * - 1 ^{( q 2} ) * - 1

^{12 h 2 (} q о ) * - 1

c * - 2

M‘ =

f( q1), M*+1

V ⁽ q о ) *

- 2 ц*+

7 q 2| M * - 1 ¹ / h ² , k = ⁽ q о )      ^J

(q1 )* f M*+1- M* 1 (q2 )* f M*- M*-11 (q0 )* V 4h J (q0 )* V 4h J

Результаты исследования и их обсуждение

Для разработанных схем повышенной (четвертой) погрешности аппроксимации установлена целесообразность их применимости для выполнения расчетов задачи водной экологии с учетом размеров вычислительной области и трудоемкости вычислений. Благодаря использованию построенных разностных схем удалось добиться снижения количества расчетных узлов сетки, покрывающих исследуемую область, и повышения точности прогностических расчетов по моделированию процессов гидробиологии мелководного водоема.

Таким образом, применение данных разностных схем способствует значительному сокращению времени реализации поставленной задачи.

Для изучения механизма наружно-гормонального регулирования взаимодействующих популяций мелководного водоема в работе использовался сценарный подход [9].

Создание комплекса программных средств прогнозного моделирования биогеохимических процессов в мелководном водоеме предполагает реализацию модельных гидробиологических задач мелководных водоемов с учетом трансформации биогеохимических циклов, включая уровень насыщения кислородом, углекислого газа, на высокопроизводительных вычислительных комплексах, что позволяет получить оперативные прогнозы экологической обстановки водоема, что, в свою очередь, является крайне важным, особенно в случае чрезвычайных ситуаций [10; 11].

Для проведения качественной калибровки и верификации созданного программноалгоритмического аппарата для выполнения прогностических расчетов гидродинамических и гидробиологических процессов в мелководных водоемах были использованы многочисленные базы экологических данных, доступные данные мониторинга исследуемой акватории, карты динамики климатических изменений, включая оперативные данные о метеоусловиях с различных метеостанций в разные сезонные временные промежутки, имеющие важное значение с точки зрения оценки влияния на динамику гидробиологических процессов, представленные на Рисунках 3, 4.

На Рисунке 3 приведены прогностические карты метеорологических условий для акватории Азовского моря Единой государственной системы информации об обстановке в Мировом океане (ЕСИМО), полученные на основе спектральной модели Wavewatch III v.3.14 системы среднесрочного метеорологического прогноза Гидрометцентра России и National Centers for Environmental Prediction (NCEP)/NOAA [12].

На Рисунке 4 цветовыми градациями представлены данные ЕСИМО, полученные в результате оперативных спутниковых и наземных наблюдений о температурном режиме поверхностного слоя Азовского моря, по данным National Climatic Data Center (NCDC)/ NOAA.

Прогностические карты метеорологических условий, разработанные сотрудниками Гидрометцентра России по имеющимся данным прогноза, выпускаемого метеоцентром NCEP/NOAA, позволяют производить оценку качества водных объектов (в данном случае – Азовского моря), осуществляемую на основе построенной математической модели процессов самоочищения (1)–(3).

На карте, представленной на Рисунке 5, показаны векторы скорости ветра (м/с) на высоте 10 м.

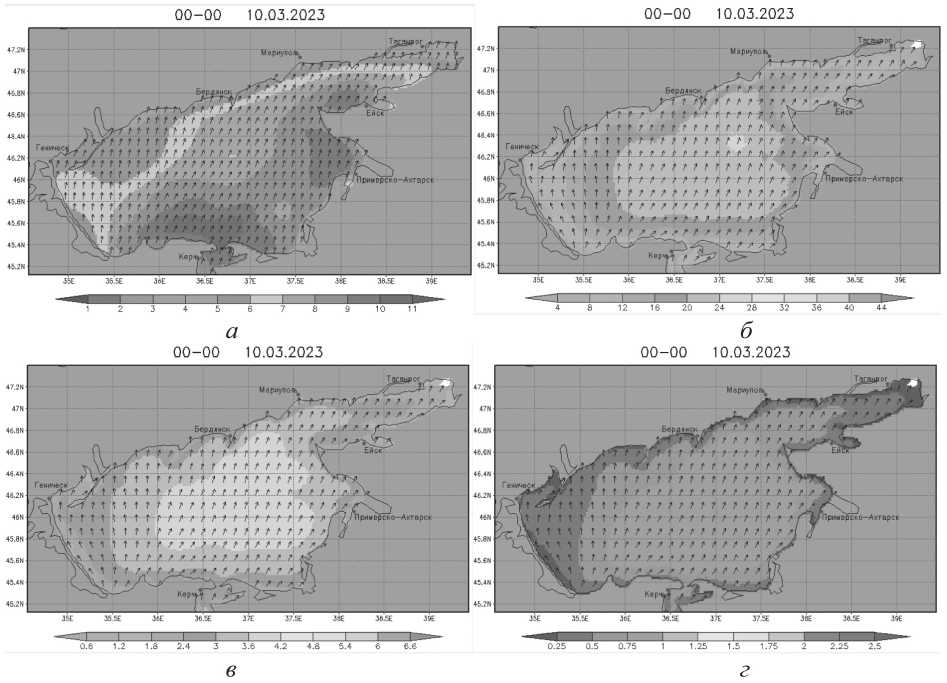
Рисунок 3. Параметры ветрового волнения: а – скорость ветра, м; б – средняя длина волн, м; в – средний период волн, с; г – высота преобладающих волн, м

Источник: Оперативный модуль ЕСИМО. URL: opermodule

Создание комплекса программных средств прогнозного моделирования динамики ...

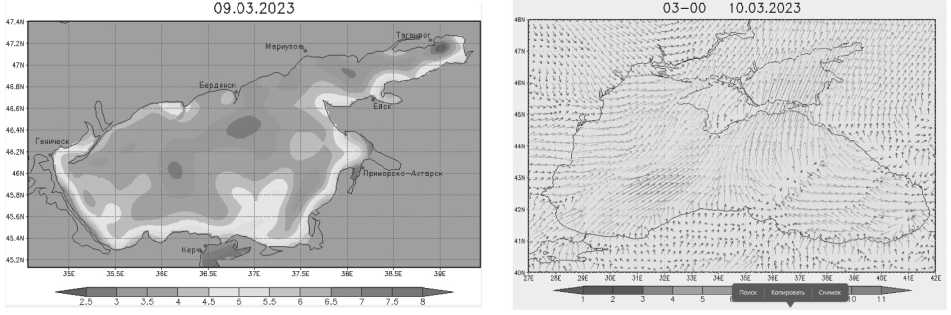
Рисунок 4. Температура поверхности воды в Азовском море, °С

Рисунок 5. Прогноз скорости ветра от 03.00 ч 10.03.2023 г.

Источник: Оперативный модуль ЕСИМО.

URL:

Заключение

Разработанный комплекс программных средств моделирования гидробиологических процессов ориентирован на высокопроизводительные вычислительные комплексы и системы, поддерживает функцию интегрирования вычислительных модулей (блоков) и может быть реализован для других мелководных систем.

Применение предложенных программных средств моделирования экологической обстановки мелководного водоема позволяет осуществлять качественный анализ и оперативное прогнозирование водных экосистем в режиме ускоренного времени, что чрезвычайно важно при природных и антропогенных явлениях, а также при возникновении чрезвычайных ситуаций.