Создание математической модели для оценки энергоёмкости процесса обеззараживания стоков животноводства

Введение. Одним из основных факторов загрязнения окружающей среды являются промышленные стоки сельского хозяйства. Наибольшую опасность представляют сточные воды животноводства (далее стоки), являющиеся

Безопасность деятельности человека

источником большого количества заболеваний, утилизация которых невозможна без их обеззараживания. Наиболее перспективным способом обеззараживания стоков является комплексное физико-химическое воздействие вращающегося переменного магнитного поля и активного хлора [1]. Энергетическим параметром качества процесса обеззараживания является удельная энергоёмкость процесса. Соответственно, создание математической модели, позволяющей оценить влияние технологических факторов на энергоёмкость процесса, является актуальной задачей.

Решить эту проблему можно используя математическую теорию планирования эксперимента.

Целью данного исследования являлось создание математической модели технологического процесса обеззараживания, оценивающей его энергетическую эффективность.

Экспериментальное исследование. Для оценки энергетической эффективности процесса необходимо рассматривать затраты электрической энергии на получение единицы готовой продукции, то есть удельной электрической энергии. В качестве единицы готовой продукции лучше всего рассматривать её объём.

На основании вышеизложенного, при оценке энергии, затраченной на технологический процесс, необходимо рассматривать активную составляющую удельной электрической энергии, расходуемой на получение единицы готовой продукции.

Представленные в табл. 1 факторы были приняты в качестве способных оказывать влияние на технологический процесс обеззараживания стоков комплексным физико-химическим воздействием в индукторе.

Таблица 1

Table 1

Факторы и уровни их варьирования в натуральных переменных

Factors and levels of their variability in physical variables

Фактор	Кодовое обозначение	Уровни факторов
		Х i = –1	Х i = 0	Х i = +1
Заполненность рабочими телами рабочей зоны индуктора ρ в %	Х 1	0,74	2,96	5,18
Отношение длины рабочих тел к их диаметру l/d	Х 2	5	15	25
Магнитная индукция B в мТл	Х 3	40	60	80
Концентрация активного хлора ω в мг/л	Х 4	6	12	18
Продолжительность воздействия t в с	Х 5	2	4	6

В качестве условий исследования рассматривались [2–5]:

• – частота колебаний электрического тока в сети f , Гц;

  – материал рабочих тел.

Кибернетическая модель системы (факторы-условия-объект исследования-параметры показатели качества), иллюстрирующая их взаимосвязь, представлена на рис. 1.

Факторы

Условия

Показатели качества

Материал рабочих тел

Р Ud

В

и

Технологический процесс обеззараживания стоков животноводства

‘Nyaa

Рис. 1. Схема кибернетической модели системы при исследовании влияния параметров технологического процесса обеззараживания стоков на его качество:

ρ — заполненность рабочими телами рабочей зоны индуктора; l/d — отношение длины рабочих тел к их диаметру; B — магнитная индукция; ω — концентрация активного хлора; t — продолжительность совместного воздействия магнитного поля, активного хлора и рабочих тел; f — частота колебаний электрического тока в сети; материал рабочих тел;

N уээ — удельная электрическая энергоёмкость процесса

Fig. 1 Cybernetic system model structure when studying effect of livestock wastes disinfection process parameters on their quality: ρ — occupancy of inductor operating area by working medium; l/d – working bodies length - their diameter ratio; B – magnetic induction; ω – concentration of active chlorine; t – duration of magnetic field, active chlorine and working medium combined exposure; f – network current oscillation frequency; working medium material; N уээ – process specific electric energy

Экспериментальные исследования проводились на индукторе, устройство и принцип действия которого описаны в [2].

Анализ источников [6, 7] и практика решения задач с помощью методов планирования эксперимента показывают, что в большинстве случаев процесс обеззараживания невозможно описать математической моделью первого порядка ввиду ее неадекватности. Значительная кривизна поверхности отклика, как правило, не позволяет описывать её уравнением первого порядка даже в весьма узкой области факторного пространства. В таких случаях необходимо описывать исследуемый процесс с помощью полиномов более высоких порядков, например, второго, имеющего вид: kk  k y = bo + E bx + E buxi + E bijxixj i=1          i=1            i=1

где    b0, bi, bii, bj — коэффициенты, характеризующие силу влияния свободных, линейных, квадратичных и эффектов взаимодействия членов уравнения.

Существует большое количество планов эксперимента, решающих определённые задачи. При выборе вида плана для конкретного эксперимента необходимо использовать характерный показатель решения задачи, по значению которого оценивается оптимальность найденного решения, то есть, максимальное удовлетворение поставленных требований. Таким показателем является критерий оптимальности плана — мера эффективности плана.

В настоящее время используется свыше 20 различных критериев оптимальности планов [8], которые подразделяются на две основные группы. К первой группе относят критерии, связанные с ошибками оценок коэффициентов, ко второй относятся критерии, связанные с ошибкой оценки поверхности отклика.

Ввиду того, что целью следующего этапа исследования является оптимизация параметров технологического процесса обеззараживания, что требует наиболее точное описания поверхности отклика, предпочтительным являются критерий G- оптимальности.

Из всего множества G- оптимальных планов или близких к ним по свойствам, с учётом количества рассматриваемых факторов, наиболее предпочтительным является план Хартли На 5. Этот план имеет минимальное количество опытов и предпочтительные статистические характеристики, по сравнению с аналогичными планами, поэтому рекомендуется для создания моделей в виде полинома второго порядка [9, 10].

Матрица плана На 5 в кодированных переменных представлена в табл. 2.

Таблица 2

Table 2 Матрица плана и результаты эксперимента

Design matrix and experimental results

Номер опыта	Уровни факторов					Удельная электрическая энергоёмкость
	Х 1	Х 2	Х 3	Х 4	Х 5	y уээ	ˆ у уээ
1	-1	-1	-1	-1	+1	7,00	7,02
2	+1	-1	-1	-1	-1	0,20	0,19
3	-1	+1	-1	-1	-1	3,60	3,59
4	+1	+1	-1	-1	+1	1,60	1,59
5	-1	-1	+1	-1	-1	9,60	9,62
6	+1	-1	+1	-1	+1	7,60	7,62
7	-1	+1	+1	-1	+1	11,00	11,02
8	+1	+1	+1	-1	-1	4,20	4,19
9	-1	-1	-1	+1	-1	4,60	4,59
10	+1	-1	-1	+1	+1	2,60	2,59
11	-1	+1	-1	+1	+1	6,00	5,99
12	+1	+1	-1	+1	-1	0,20	0,17
13	-1	-1	+1	+1	+1	12,00	12,02
14	+1	-1	+1	+1	-1	5,20	5,19
15	-1	+1	+1	+1	-1	8,60	8,60
16	+1	+1	+1	+1	+1	6,60	6,59
17	-1	0	0	0	0	9,30	9,25
18	+1	0	0	0	0	4,90	4,96
19	0	-1	0	0	0	4,60	4,55

Безопасность деятельности человека

20	0	+1	0	0	0	3,60	3,66
21	0	0	-1	0	0	3,10	3,16
22	0	0	+1	0	0	8,10	8,05
23	0	0	0	-1	0	5,60	5,55
24	0	0	0	+1	0	5,60	5,66
25	0	0	0	0	-1	4,40	4,46
26	0	0	0	0	+1	6,80	6,75
27	0	0	0	0	0	5,60	5,59

Согласно принятому плану было реализовано 27 опытов. Для уменьшения систематических ошибок опыты проводились в случайном порядке. Каждый опыт дублировался три раза.

Полученные в результате опытов средние значения контролируемых параметров представлены в табл. 2.

Проверка полученных значений оценок дисперсий параллельных опытов на однородность по критерию Кохрена показала, что при выбранном уровне значимости а = 0,05 и степенях свободы числителя f_K1 = 2 и знаменателя f_K2 =27 расчетные значения G р меньше критического значения G к = 0,21 [11]. Следовательно, гипотеза об однородности дисперсий параллельных опытов справедлива.

После определения оценок коэффициентов, их характеристик и исключения функций из уравнения при статистически незначимых коэффициентах, уравнение регрессии для удельной электрической энергоёмкости принимает вид:

у уээ = 5,59 - 2,14 x - 0,44 x ₂ + 2,24 x₃ + 1,14 x ₅ + 1,52 x 2 - 1,48 x 2                          (1)

По полученным уравнениям были рассчитаны значения удельной электрической энергоёмкости y ˆ уээ , представленные в табл. 2.

Проверка полученных уравнений на адекватность по F -критерию показала, что при выбранном уровне значимости а = 0,05 и соответствующих степенях свободы f ag и f e расчетные значения F p меньше критического значения F k . Следовательно, гипотеза об адекватности уравнений справедлива.

После подстановки переходных коэффициентов и преобразования уравнение регрессии удельной электрической энергоёмкости приняло вид:

N _уээ = 4,815 - 2,789 р + 0,400 l / d + 0,112 В + 0,570 t + 0,308 р ² - 0,014 l / d ²                     (2)

Уравнение (2) даёт возможность рассчитать значения удельной электрической энергоёмкости N уээ для любых точек, находящихся внутри области изучаемого факторного пространства.

На основании экспериментальных данных (табл. 2) были построены графические зависимости, представленные на рис. 2 и 3.

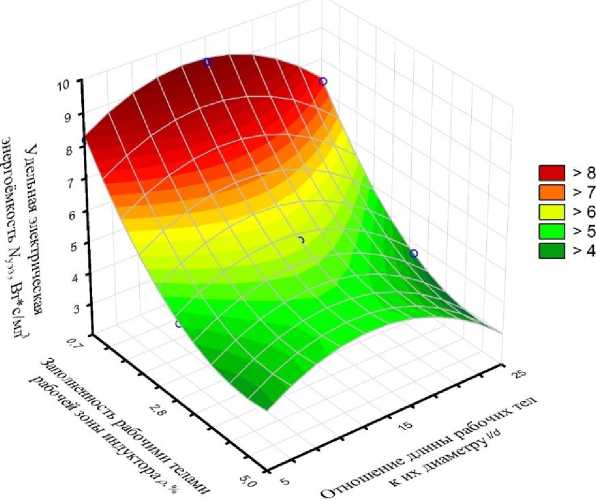
Рис. 2. Зависимость удельной электрической энергоёмкости процесса обеззараживания от факторов, связанных с рабочими телами

Fig. 2. Dependence of specific electric power intensity of disinfection process on factors connected to working medium

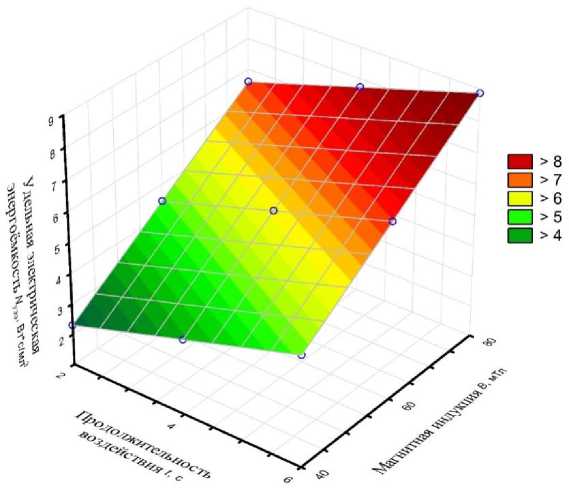
Рис. 3. Зависимость удельной электрической энергоёмкости процесса обеззараживания от магнитной индукции и продолжительности совместного воздействия магнитного поля и рабочих тел

Fig. 3. Dependence of specific electrical energy intensity of disinfection process on magnetic induction and duration of combined exposure of magnetic fields and working medium

Анализ результатов. Анализ результатов опытов и расчётов (табл. 2), уравнений (1), (2) и графических зависимостей (рис. 2, 3) показал:

• -    уравнение в кодированных (1) и натуральных (2) переменных в виде полинома второй степени адекватно по критерию Фишера характеризуют зависимость удельной электрической энергоёмкости от рассматриваемых факторов при уровне значимости а = 0,05. Поэтому оно может служить в качестве математической модели процесса обеззараживания стоков;

При исследовании влияния рассматриваемых факторов в области интереса на удельную электрическую энергоёмкость установлено:

• -    статистически не значимыми, в рассматриваемом диапазоне факторов, оказались оценки коэффициентов концентрации активного хлора в пробе, на что указывает отсутствие членов уравнения х₄ (1) или в натуральных переменных ю (2);

• -    заполненность рабочими телами рабочей зоны индуктора р существенно влияет на удельную электрическую энергоёмкость, на что указывают оценки коэффициентов членов уравнения х 1 (1) или в натуральных переменных р (2). При этом, с возрастанием значений заполненности рабочими телами рабочей зоны, происходит убывание значений удельной электрической энергоёмкости по квадратичной зависимости, на что указывает существенная оценка коэффициента х 2 (1) или в натуральных переменных р ² (2);

• -    отношение длины рабочих тел к их диаметру l/d существенно влияет на удельную электрическую энергоёмкость, на что указывают оценки коэффициентов членов уравнения Х 2 (1) или в натуральных переменных l/d (2). При этом, с возрастанием значений отношения длины рабочих тел к их диаметру l/d , происходит убывание значений удельной электрической энергоёмкости по квадратичной зависимости, на что указывает существенная оценка коэффициента х 2 (1) или в натуральных переменных р ² (2);

• -    магнитная индукция В существенно влияет на удельную электрическую энергоёмкость, на что указывают оценки коэффициентов членов уравнения х₃ (1) или в натуральных переменных В (2). При этом, с возрастанием значений магнитной индукции В , происходит возрастание значений удельной электрической энергоёмкости по линейной зависимости, на что указывает несущественная оценка коэффициента х 2 (1) или в натуральных переменных В² (2);

• -    концентрация активного хлора в пробе ю не существенно влияет на удельную электрическую энергоёмкость, на что указывает отсутствие членов уравнения х₄ (1) или в натуральных переменных ю (2);

• -    продолжительность совместного воздействия магнитного поля, активного хлора и рабочих тел на пробу t существенно влияет на удельную электрическую энергоёмкость, на что указывают оценки коэффициентов членов

  Безопасность деятельности человека

  
  

уравнения x 5 (1) или в натуральных переменных t (2). При этом, с возрастанием значений продолжительности совместного воздействия магнитного поля, активного хлора и рабочих тел на пробу t , происходит возрастание значений удельной электрической энергоёмкости по линейной зависимости, на что указывает несущественная оценка коэффициента х 52 (1) или в натуральных переменных t 2 (2);

• –    несущественными оказались все оценки коэффициентов парного взаимодействия, что указывает на отсутствие эффекта парного взаимодействия рассмотренных факторов;

• –    сила влияния факторов распределилась следующим образом: магнитная индукция; заполненность рабочими телами рабочей зоны индуктора; продолжительность совместного воздействия магнитного поля, активного хлора и рабочих тел на пробу; отношение длины рабочих тел к их диаметру.

Заключение. Анализ результатов опытов (табл. 2), расчётов (табл. 2), уравнений (1), (2) и графических зависимостей (рис. 2, 3) позволили оценить влияние ряда технологических факторов на удельную электрическую энергоёмкость процесса, а также наметить гипотезы, объясняющие физическую сущность процессов, происходящих при обеззараживании стоков животноводства путём комплексного физико-химического воздействия магнитного поля и активного хлора.