Создание математической модели рулевого тракта космического ракетного блока и исследование влияния гидравлических сил в рулевой машине на его устойчивость

В системах управления движением ракетных блоков выделяют специальные подсистемы, отвечающие за управление угловым положением камер сгорания маршевых двигателей этих изделий в плоскостях стабилизации. Каждая из таких подсистем, называемая системой управления вектором тяги (СУВТ) [1], включает в себя два канала управления, или рулевых тракта (РТ), содержащих электрогид-равлические рулевые машины (РМ). Типовая конструкционная схема РТ с электрогидравлической РМ показана на рис. 1. Каждый РТ содержит, как правило, свой блок обратной связи, включающий усилитель, сумматор и фильтр электрических сигналов. В таком РТ камера сгорания маршевого двигателя устанавливается в карданном подвесе, благодаря чему рулевые машины имеют возможность поворачивать камеру одновременно в двух плоскостях стабилизации. Схема типовой автономной однокаскадной электро-гидравлической РМ с двухдроссельным электрогидравлическим усилителем (ЭГУ) разгонного блока (РБ) приведена на рис. 2.

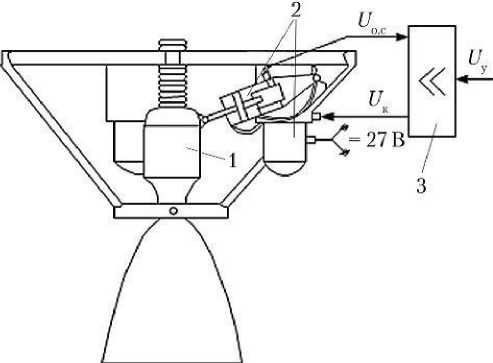
Рис. 1. Конструкционная схема рулевого тракта (РТ): 1 — камера маршевого двигателя; 2 — рулевая машина; 3 — аппаратура обратной связи; U _о.с — напряжение обратной связи; U _у — управляющее напряжение на входе РТ; U _к — командное напряжение (рисунок создан автором)

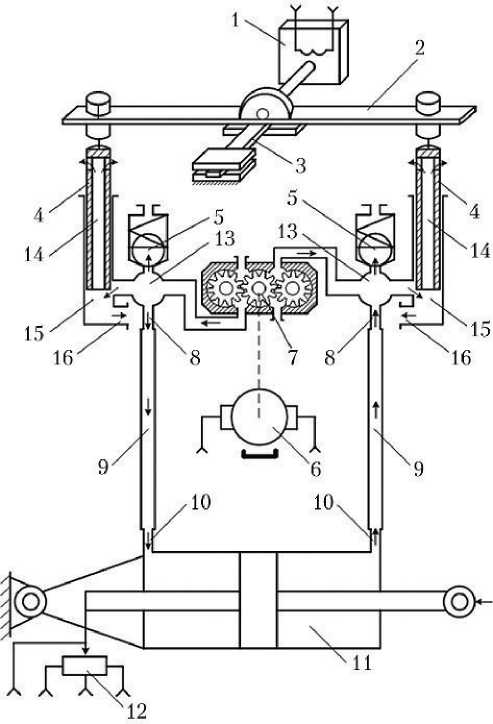
Рис. 2. Схема рулевой машины с двухдроссельным электрогидравлическим усилителем: 1 — электромеханический преобразователь; 2 — коромысло; 3 — плоская нагрузочная пружина; 4 — золотниковые плунжеры; 5 — предохранительный клапан; 6 — электродвигатель; 7 — трёхшестерённый насос; 8 — входные каналы трубопроводов; 9 — трубопроводы; 10 — выходные каналы трубопроводов; 11 — силовой гидроцилиндр; 12 — потенциометр обратной связи; 13 — рабочая полость электрогидравлического усилителя; 14 — канал золотника; 15 — канал гильзы; 16 — канал слива [2]

Дифференциальные уравнения математической модели, описывающие процессы сжатия рабочей жидкости в полостях ЭГУ РМ, в общем виде записываются следующим образом [3]:

V dp

^Е ж ^dt

n ∑ Q i , i = 1

где V — объём полости силового гидроцилиндра; Е _ж — модуль объёмной упругости жидкости; p — давление в полости; Q_i — i -й расход жидкости, поступающий в полость; n — количество расходов, поступающих в полость.

Если преобразовать эти дифференциальные уравнения к операторному виду, т. е. представить их в виде апериодических звеньев первого порядка, а затем определить постоянные времени и собственные частоты этих звеньев (таблица), то можно увидеть, что собственные частоты процессов сжатия рабочей жидкости в полостях ЭГУ из-за малости их объёмов лежат далеко за пределами полосы пропускания узла управления (УУ) ЭГУ РМ, составляющей 10 Гц [4].

Собственные частоты процессов сжатия рабочей жидкости в полостях ЭГУ

Полость	Объём полости, см3	Постоянная времени, с	Собственная частота, Гц
Рабочая	0,5737	4,6266 ⋅ 10–5	3 441,7
Канала золотника	0,1828	1,4742 ⋅ 10–5	10 801,5
Канала гильзы	0,1257	1,0137 ⋅ 10–5	15 708,3
Канала слива	0,5000	4,0322 ⋅ 10–5	3949,1

Следовательно, рабочую жидкость в полостях ЭГУ РМ можно считать несжимаемой. При допущении о несжимаемости рабочей жидкости в полостях ЭГУ, наиболее распространённой формой представления их структуры является описание выходного силового каскада ЭГУ совместно с источником гидравлической мощности обобщённым уравнением следующего вида [5]:

Q = Q ( X _з , Δ р ), (1)

где Q — расход жидкости между рабочими полостями ЭГУ; X _з — перемещение золотникового плунжера; Δ р — перепад давления между рабочими полостями ЭГУ, — т. е. описание выходного каскада ЭГУ семейством его расходно-перепадных характеристик.

С другой стороны, на золотниковые плунжеры гидрораспределителя ЭГУ РМ действует гидравлическая сила со стороны обтекающих их потоков рабочей жидкости F _г , которую можно представить в виде суммы гидростатической силы F _г.с , стационарной составляющей гидродинамической силы F _г.д.с и нестационарной составляющей гидродинамической силы F _г.д.н [6].

Известно [7], что нестационарные составляющие гидродинамических сил Fг.д.н пропорциональны длинам демпфирования, поэтому в гидрораспределителях ЭГУ РМ во избежание неустойчивости их стараются уравнять и максимально уменьшить, для чего конструкцию гидрораспределителя ЭГУ выполняют симметричной с равными длинами демпфирования нагнетания и слива. Кроме этого, вращение ведомых осей трёхшестерённого насоса, исполняющих роль гильз золотниковых плунжеров, делает длины демпфирования пренебрежимо малыми. По этим причинам полагают, что нестационарные составляющие гидродинамических сил взаимно уничтожаются [8], а на золотниковые плунжеры ЭГУ действуют только гидростатические силы и стационарные составляющие гидродинамических сил:

^F г ^{= F} г.с ^{+ F} г.д.с^.

В работе [6] показано, что суммы гидростатической и стационарной составляющей гидродинамической силы, действующие на золотниковые плунжеры рассматриваемого ЭГУ, могут быть сведены к функциям, зависящим от параметров Δ р и Q , т. е.

F _г = F _г ( Q , Δ р ).

Постановка задачи

Для исследования влияния гидравлических сил, действующих на золотниковые плунжеры ЭГУ рулевых машин и устойчивость СУВТ, необходимо располагать адекватной математической моделью РТ.

Применение подробной математической модели для практического моделирования РТ СУВТ маршевого двигателя космического РБ, выполненного на базе электрогидравлической РМ, затруднительно из-за необходимости выбора весьма малого шага при численном интегрировании системы дифференциальных уравнений. Поэтому на практике стремятся использовать упрощённые математические модели, пригодные для работы в системах автоматизированного моделирования, имеющих встроенный математический аппарат анализа устойчивости и оценки качества регулирования.

Для создания упрощённой математической модели рулевого тракта необходимо располагать точными аппроксимациями семейств расходно-перепадных характеристик и семейств зависимостей гидравлических сил от расхода и перепада давления между рабочими полостями ЭГУ РМ, которые, как это явствует из приведённых выше формул (1) и (2), являются двумерными. При этом в работе [9] отмечено, что линейная аппроксимация расходно-перепадной характеристики ЭГУ может привести к неправильной оценке условий существования автоколебаний в гидроприводе.

В большинстве случаев эти зависимости носят нелинейный или трансцендентный характер, что иллюстрируется рис. 3 и 4, и до недавнего времени для их аппроксимации требовалось создание достаточно сложных аналитических моделей [6].

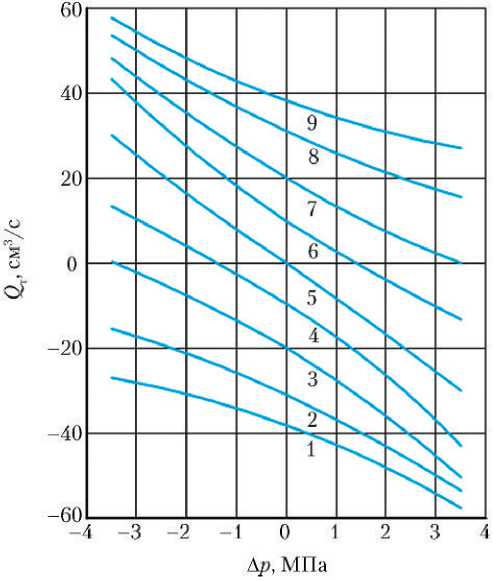
Рис. 3. Семейство экспериментальных расходно-перепадных характеристик электрогидравлического усилителя (ЭГУ) рулевой машины: Q _т — расход через трубопровод; Δ р — перепад давления между рабочими полостями ЭГУ; 1 — перемещение золотникового плунжера X _з = –0,020 см; 2 — X _з = –0,015 см; 3 — X _з = –0,010 см; 4 — X _з = –0,005 см; 5 — X _з = 0 см; 6 — X_з = 0,005 см; 7 — X_з = 0,010 см; 8 — X_з = 0,015 см; 9 — X _з = 0,020 см (рисунок создан автором)

С развитием компьютерной техники появилась возможность аппроксимировать такие зависимости с помощью разработанного автором метода многомерной кубической сплайн-интерполяции-экстраполяции (КСИЭ) [10], однако его внедрение в моделирование составляющих элементов РТ долгое время сдерживалось низким уровнем быстродействия вычислительной техники.

Стремительное развитие вычислительной техники и совершенствование её характеристик (в частности, её быстродействия) в настоящее время позволяют практически полностью переориентировать аналитические методы аппроксимации на методы многомерной КСИЭ.

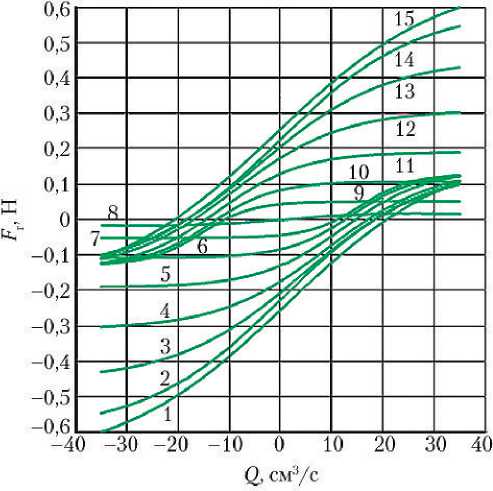
Рис. 4. Семейство экспериментальных зависимостей гидравлических сил F _г от расхода Q и перепада давления между рабочими полостями электрогидравлического усилителя рулевой машины Δ р: 1 — Δ р = –3,5 МПа; 2 — Δ р = –3,0 МПа; 3 — Δ р = –2,5 МПа; 4 — Δ р = –2,0 МПа; 5 — Δ р = –1,5 МПа; 6 — Δ р = –1,0 МПа; 7 — Δ р = –0,5 МПа; 8 — Δ р = 0 МПа; 9 — Δ р = 0,5 МПа; 10 — Δ р = 1,0 МПа; 11 — Δ р = 1,5 МПа; 12 — Δ р = 2,0 МПа; 13 — Δ р = 2,5 МПа; 14 — Δ р = 3,0 МПа; 15 — Δ р = 3,5 МПа (рисунок создан автором)

Отличительная особенность этих методов заключается в том, что аналитические зависимости характеристик не требуются, а в расчётах статических или динамических характеристик по соответствующим математическим моделям используются табличные представления экспериментальных данных.

Описание методов, алгоритмов и программ КСИЭ для одномерных табличных зависимостей представлено в работах [11, 12].

В настоящей работе ставится задача применения метода многомерной КСИЭ [10] для аппроксимации семейств рас-ходно-перепадных характеристик и семейств зависимостей гидравлических сил от расхода и перепада давления между рабочими полостями ЭГУ РМ РБ ДМ с последующей интеграцией этих аппроксимаций в математическую модель РТ.

Разработка упрощённой математической модели и структуры ЭГУ РМ

В соответствии с методом многомерной КСИЭ [10] функцию аппроксимации семейства расходно-перепадных характеристик Q = Q ( Δ р , X _з ) удобно определить функцией двумерной КСИЭ

Q = spl( Δ р , X _з ).

Аналогичным образом функцию аппроксимации семейства зависимостей гидравлических сил от расхода и перепада давления между рабочими полостями ЭГУ РМ можно определить функцией двумерной КСИЭ

F _г = spl( Q , Δ р ). (4)

Для обеих функций двумерной КСИЭ (3) и (4) в математической модели РТ были выполнены процедуры-функции, реализующие функции указанных двумерных КСИЭ с вложенными в них двумерными массивами экспериментальных данных.

Таким образом, для разработки упрощённой математической модели РТ СУВТ необходимо решить задачу структурно-параметрического синтеза ЭГУ, т. е. сформировать его структуру и определить параметры.

Математическая модель УУ ЭГУ РМ [4] с учётом погружения в рабочую жидкость и действия на золотниковые плунжеры гидравлических сил со стороны обтекающих их потоков рабочей жидкости, с учётом ограничения может быть представлена следующими уравнениями:

• •    уравнением баланса напряжений в цепи электромеханического преобразователя (ЭМП) :

L ^{dI к} + RI + K γ = U , _dt         к э       к^,

где L — индуктивность обмоток ЭМП; I _к — командный ток; t — текущее время; R — активное сопротивление обмоток ЭМП; K _э — коэффициент электромагнитной скоростной связи; γ — угловая скорость движения валика ЭМП; U _к — командное напряжение;

• уравнением баланса моментов, приведённых к валику ЭМП:

d α _dt = γ ;

d γ Σ M dt J ^,

где α — угол поворота валика ЭМП; J — момент инерции подвижных частей УУ, приведённый к валику ЭМП; Σ M — результирующая сумма моментов, действующих на валик ЭМП, для режимов покоя и движения определяемая следующим образом:

K _м I _к – M _с.т sign( γ ) – K _м.в γ – – K _м.п α – R _α F _г при γ ≠ 0;

Σ M =

K _м I _к – M _с.т sign( K _м I _к – K _м.п α – R – K _м.п α – R _α F _г при γ = 0 и | K м I к – K м.п α – R α F г | >  M с.т ;

α F г ) –

0 при γ = 0

и |KмIк – Kм.пα – RαFг| ≤ Mс.т, где Kм — коэффициент входного момента; Kм.п — коэффициент позиционного момента; Rα — плечо коромысла УУ электрогидравлического усилителя РМ; Mс.т — момент сухого трения, приведённый к валику ЭМП; Kм.в — коэффициент момента вязкого трения УУ, приведённый к валику ЭМП;

• •    уравнением кинематической связи между углом поворота валика ЭМП и перемещением золотникового плунжера X _з для малых углов поворота валика:

  X _з = R _α sin( α ) ≅ R _αα ;

  
  
  
  

• •    уравнением ограничения, накладываемого на угол поворота валика ЭМП:

| α | >  α _max ,                                      (9)

где α _max — максимальный угол поворота валика ЭМП.

Для разработки структуры упрощённой математической модели ЭГУ сделаем следующие допущения:

• •    поскольку возможность открытия предохранительных клапанов РМ при нормальном функционировании РМ является маловероятной, ограничиваемся диапазоном значений перепадов давления Δ p , не превышающим по модулю давление начала открытия предохранительных клапанов p _{к min} , т. е.

|Δp| ≤ p к min

• •    поскольку производительность каждой секции трёхшестерённого насоса имеет естественное ограничение, обусловленное максимальной угловой скоростью вращения вала приводного электродвигателя РМ при отсутствии нагрузки на вале (холостой ход), расход рабочей жидкости между рабочими полостями ЭГУ Q также целесообразно ограничить диапазоном расходов, по модулю не превышающим максимальную теоретическую производительность одной секции трёхшестерённого насоса на холостом ходу приводного электродвигателя Q _max , т. е.

Для режима движения, после преобразования уравнений (5), (6) и (7)

к виду

R

U к – K э ^d _d ^α _t

L dI к + I;

R dt ^к

• ^{d 2 α K} м ^I к ^{– M} с.т ^{sign( γ ) – K} м.в ^{γ – K} м.п ^{α – R} α ^F г , (13) dt ² J

с учётом уравнения (8), параметрических ограничений (9), (10) и (11), а также функций двумерной кубической сплайн-интерполляции-экстраполя-ции (3) и (4), искомая структура ЭГУ может быть представлена в виде, приведённом на рис. 5, где T ₁ = L / R .

Методы многомерной кубической сплайн-интерполяции-экстраполяции применительно для аппроксимации гидравлических характеристик элементов рулевых машин ракетных блоков изложены в работе [9].

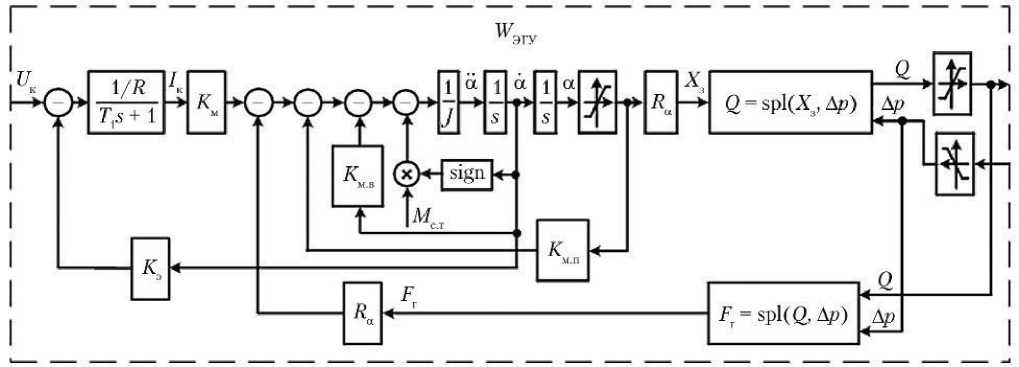
Рис. 5. Структура упрощённой математической модели электрогидравлического усилителя (ЭГУ): W _ЭГУ — передаточная функция ЭГУ; U _к — командное напряжение; R — активное сопротивление обмоток электромеханического преобразователя (ЭМП); Т ₁ — постоянная времени ЭМП; s — оператор Лапласа; I _к — командный ток; K _м — коэффициент входного момента; J — момент инерции подвижных частей узла управления (УУ); α — угол поворота валика ЭМП; R _α — плечо коромысла УУ ЭГУ; Δ p и Q — перепад давления и расход жидкости между рабочими полостями ЭГУ соответственно; X _з — перемещение золотникового плунжера; K _м.в — коэффициент момента вязкого трения УУ, приведённый к валику ЭМП; K _э — коэффициент электромагнитной скоростной связи; K _м.п — коэффициент позиционного момента; M _с.т — момент сухого трения, приведённый к валику ЭМП; F _г — гидравлическая сила, действующая на золотниковые плунжеры со стороны обтекающих их потоков рабочей жидкости (рисунок создан автором)

Разработка упрощённойматематической модели и структуры РТ

Перед выводом уравнений упрощённой математической модели РТ его конструкционная схема (см. рис. 1) была приведена к расчётной схеме, представленной на рис. 6.

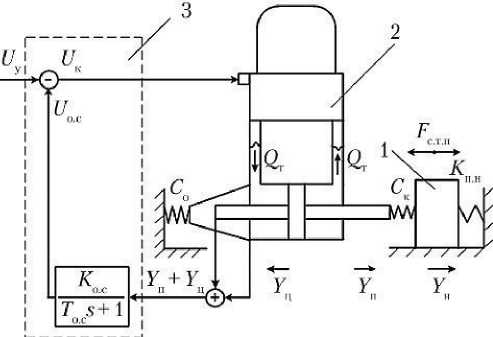
Рис. 6. Расчётная схема рулевого тракта (РТ): 1 — нагрузка; 2 — рулевая машина (РМ); 3 — аппаратура обратной связи; U _у — управляющее напряжение на входе РТ; U _к — командное напряжение; U _о.с — напряжение обратной связи; Q _т — расход через трубопровод; С _о — коэффициент упругости места соединения основания корпуса силового гидроцилиндра с рамой объекта управления (нагрузки); С _к — коэффициент упругости места соединения штока силового гидроцилиндра РМ с объектом управления (нагрузкой); F _с.т.н — сила сухого трения в объекте управления; K _п.н — коэффициент позиционной нагрузки; K _о.с — коэффициент усиления сети обратной связи; Т _о.с — постоянная времени фильтра в цепи обратной связи; s — оператор Лапласа; Y _п и Y _ц — перемещение поршня и корпуса силового гидроцилиндра соответственно; Y _н — перемещение нагрузки (рисунок создан автором)

Перед выводом уравнений упрощённой математической модели РТ были сделаны следующие допущения:

• •    из-за кратковременности моделируемых процессов РТ температура рабочей жидкости и конструкций ЭГУ и РМ полагается постоянной и равной температуре нормальных климатических условий;

• •    так как объёмы полостей ЭГУ малы, процессами сжатия рабочей жидкости в них можно пренебречь.

Уравнения баланса расходов в полостях силового гидроцилиндра РМ в таком случае определяются следующими соотношениями [6]:

Q т1 – S п

dY п d t

dY

ц dt

V + S(Y + L ) dp о п п0 п

Edt

ж dYdY

+ S – ^ц –

• 2 п d tdt

V + S (Y – L ) dp о п п0 п 2

Edt

ж

где Qт1 и Qт2 — расходы рабочей жидкости, поступающие от ЭГУ в первую и вторую полости силового гидроцилиндра РМ соответственно; Sп — эффективная площадь поршня силового гидроцилиндра; Yп и Yц — перемещение поршня и корпуса силового гидроцилиндра соответственно; Vо — остаточный объём полости силового гидроцилиндра при постановке его поршня на упор (обычно с учётом ёмкости соединительного трубопровода и рабочей полости ЭГУ); Yп0 — длина полости силового гидроцилиндра при среднем положении поршня; Eж — модуль объёмной упругости рабочей жидкости; p1, p2 — давления рабочей жидкости в первой и второй полостях силового гидроцилиндра РМ соответственно; Lп — параметр, определяемый, как в работе [6]:

S п Δ p – F с.т.ц sign( V п – V ц ) –

– C к ( Y п – Y н ) при ( V п – V ц ) ≠ 0;

S _п Δ p – F _с.т.ц sign[ F _с.т.ц Δ p –

₌    – C _к ( Y _п – Y _ц )] – C _к ( Y _п – Y _н )

^п при ( V _п – V _ц ) = 0 и

| S п Δ p – C к ( Y п – Y ц )| >  F с.т.ц ;

0 при ( V _п – V _ц ) = 0 и | S п Δ p – C к ( Y п – Y ц )| ≤ F с.т.ц ;

L = п

Y _п – Y _ц при | Y _п – Y _ц | <  Y _{п 0} ;

Y _{п 0} sign( Y _п – Y _ц ) при | Y _п – Y _ц | ≥ Y _{п 0} .

dY

___ц dt

< dV

____ц dt

- Vц

ΣF ц .

;

m ц

При переходе к обобщённым параметрам Q = Qт1 = Qт2 и Δp = p1 — p2, а также допущении о том, что величины сжимаемых объёмов в силовом гидроцилиндре РМ практически не из- меняются при малых перемещениях поршня, в соответствии с работой [5] уравнения (14) и (15) могут быть приведены к известному уравнению, определяющему баланс расходов [6]:

dY   dY V d∆p п – ц +             , п d t     dt     2E dt

ж

где V — объём полости силового гидроцилиндра,

V = V _о + S _п Y _{п 0} .

Для режимов покоя и движения, уравнения баланса сил, приведённых к поршню и к корпусу силового гидроцилиндра РМ, а также выражения для действующих на них результирующих сил, в соответствии с работой [6] могут быть определены следующим образом:

dY п dt

= V п ;

dV   ΣF п= п dt m п

S п Δ p – F с.т.ц sign( V п – V ц ) – C 0 Y ц при ( V _п – V _ц ) ≠ 0;

S _п Δ p – F _с.т.ц sign( S _п Δ p –

=   – C 0 Y ц) – C 0 Y ц ц при ( V п – V ц) = 0 и |SпΔp – C0Yц| > Fс.т.ц ;

0 при (Vп – Vц) = 0 и |SпΔp – C0Yц| ≤ Fс.т.ц , где Cк — коэффициент упругости места соединения штока силового гидроцилиндра РМ с объектом управления (нагрузкой); Yн — перемещение нагрузки; Cо — коэффициент упругости места соединения основания корпуса силового гидроцилиндра с рамой объекта управления (нагрузки); Fс.т.ц — сила сухого трения в силовом гидроцилиндре РМ; ∑Fп и ∑Fц — суммы сил, действующих на поршень и корпус силового гидроцилиндра соответственно; mп и mц — масса поршня и корпуса силового гидроцилиндра РМ соответственно.

Для проведения дальнейших упрощений объект управления РТ представим в виде суммы инерционной, позиционной и постоянно действующей нагрузок, а также нагрузки в виде силы сухого кулоновского трения. При этом аппаратуру обратной связи представим в виде усилителя-сумматора с фильтром высокочастотных сигналов в цепи обратной связи.

В этом случае для режимов покоя и движения уравнение баланса сил, приведённых к объекту управления, а также выражение для действующей на него результирующей силы, в соответствии с работой [6] можно записать в следующем виде:

dY н dt

= V н ;

dV н dt

EF

н

;

m н

C _к ( Y _п – Y _н ) – F _с.т.н sign( V _н ) – – K _п.н Y _н – F _п.н при V _н ≠ 0;

E F

н

C к ( Y n — Y н ) — ^F c^ sign[ C к ^x

* ( Y n — Y H ) — K _n. Y н — F nJ —

– K _п.н Y _н – F _п.н при V _н = 0 и

| C к ( Y п – Y н ) – K п.н Y н – F п.н | >  F с.т.н ;

0 при V _н = 0 и

|Cк(Yп – Yн) – Kп.нYн – Fп.н| ≤ Fс.т.н, где Fс.т.н — сила сухого трения в объекте управления; Kп.н — коэффициент позиционной нагрузки; Fп.н — постоянно действующая нагрузка; ∑Fн — сумма сил, действующих на объект управления (результирующая сила); mн — масса объекта управления;

Уравнение баланса напряжений в цепи обратной связи можно определить следующим выражением [6]:

T ^{dU о.с} + U = K ( Y – Y ),        (23)

о.с                   о.с о.с п ц а уравнение баланса напряжений в усилителе-сумматоре выражением [6]

U к = U у – U о.с ,                            (24)

где Uу — управляющее напряжение на входе РТ; Uо.с — напряжение обратной связи; Tо.с — постоянная времени фильтра в цепи обратной связи; Kо.с — коэффициент усиления цепи обратной связи.

Перед выводом уравнений упрощённой математической модели РТ СУВТ примем следующие допущения:

• •    массами подвижных частей силового гидроцилиндра РМ пренебрегаем, так как они значительно меньше приведённой массы объекта управления;

• •    силу сухого трения между поршнем силового гидроцилиндра и его корпусом относим к силе сухого трения в объекте управления;

• •    направление координаты перемещения корпуса силового гидроцилиндра РМ изменяем на противоположное.

С учётом принятых допущений системы уравнений (17) и (18) баланса сил, действующих на поршень силового гидроцилиндра РМ, вырождаются в соответствии с работой [6]:

C к ( Y п – Y н ) = S п Δ p , (25)

а системы уравнений (19) и (20) баланса сил, действующих на корпус силового гидроцилиндра РМ, вырождаются в соответствии с работой [6]:

C о Y ц = S п Δ p . (26)

При этом уравнение баланса напряжений в цепи обратной связи (23) преобразуется к следующему виду [6]:

T ^о.с + U = K ( Y + Y ).         (27)

о.с                  о.с о.с п ц

Из выражения (25) следует, что

Y _п = Y _н + _C ^{S п} Δ p ,                      (28)

а из выражения (26) следует, что [6]:

S

Y ц = C п Δ p .                           (29) о

Тогда, продифференцировав выра-

жения (28) и (29), получаем [6]:

dY   dY   S d ∆ p п = н + п        ;                  (30) dt     dt     C dt к

dY   S d ∆ p

dt ц = C п d t .                        (31) o

Подставляя выражения (30) и (31) в уравнение (16), получаем следующее выражение [6]:

dYн + Sп d∆p + S Sп d∆p + V d∆p п d t    C d t      п C d t     2 E d t к  ож

dY

= S ^н + S ² п d t

п

C к

1 +

C

^{d ∆ p} + dt

V   d∆p    dY    S2

= S ^н + ^п +

2E   dt п d tC ж                          крж

d ∆ p      dY 2 E S ² + VC  d ∆ p

= S н + ж п кр dt п d t      2E C dt ж кр

где C _кр

C _к C _о

упругость

— +

C ⁺ к

C о

мест

_{C + C} — суммарная ко

крепления силового

гидроцилиндра РМ.

Из выражения (32) получаем [6]:

d ∆ p dt

2 E ж С кр

2 E S ² + VC

жп

кр

или

d ∆ p dt

KQ – S п

dY

н

п

где

K =

2 E ж C кр

Q

dt ^,

2 E _ж S _п ² + VC _кр

.

dY

– S ^н п _dt

Тогда ∑ F _н будет определяться

как

Σ F = н

dY

S Δp – F  sign н п          с.т.н          dt

dY

– K Y – F при ^н ≠ 0;

п.н н п.н           dt

S _п ∆ p – F _с.т.н sign( S _п ∆ p –

– K п.н Y н – F п.н) – K п.н Y н – F п.н dY при d t н = 0 и

| S _п ∆ p – K _п.н Y _н – F _п.н | >  F _с.т.н ;

dY

0 при ^н = 0 и dt

| S п ∆ p – K п.н Y н – F п.н | ≤ F с.т.н .

Совокупность уравнений (3)–(21), (24), (27)–(31), (33) и (34) представляет собой упрощённую математическую модель РТ СУВТ с РМ, содержащей двухдроссельный ЭГУ.

Обобщённая структура полученной упрощённой математической модели РТ СУВТ с РМ, содержащей двухдроссельный ЭГУ, для режима движения представлена на рис. 7.

На рис. 8 представлены экспериментальные и расчётные переходные характеристики РТ СУВТ с РМ, содержащей двухдроссельный ЭГУ, при единичных входных ступенчатых сигналах управления U _у = 0,5 В; U _у = 1,0 В и U _у = 1,5 В, рассчитанные при R = 200 Ом;

J = 2,5·10^–3 Н·см·с²/рад;

L = 2,6 Гн;

K _э = 1,6 В·с/рад;

K _м = 2,04048 Н·м/А;

R _α = 1,5 см;

V _o = 23,0 см³;

K _м.п = 130,0 Н·см/рад;

K _мв = 0,05 Н·см·с/рад;

S _п ^.= 9,62 см²;

Y п 0 = 1,7 см;

E _ж = 1,24·10⁵ Н/см²;

С _к = 6·10⁵ Н/см;

С ^к _о = 4,3·10⁴ Н/см;

Q = 45 см³/с;

max pк min = 4 МПа;

m _н = 5 Н·с²/см;

F _с ^н _{т н} = 400 Н;

K _п ^. _н ^. = 800 Н/см;

F _п ^п _н ^.н = 200 Н;

K ^п _о ^.н _.с = 7,06 В/см.

Анализ графиков переходных характеристик, представленных на рис. 8, показывает, что расчётные данные демонстрируют хорошую сходимость с результатами эксперимента (максимальное отклонение не превышает по модулю 2%). Следовательно, задачу создания упрощённой математической модели РТ СУВТ с РМ, содержащей двухдроссельный ЭГУ, можно считать решённой.

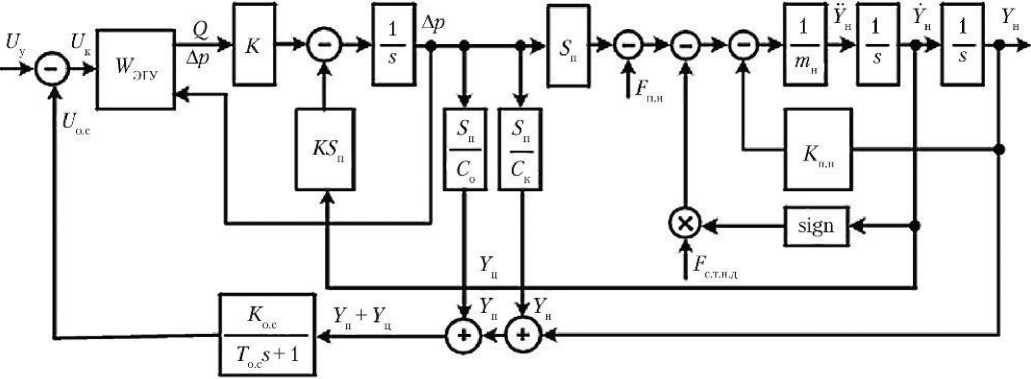
Рис. 7. Структура упрощённой математической модели рулевого тракта (РТ): U _у — управляющее напряжение на входе РТ; U _к — командное напряжение; U _о.с — напряжение обратной связи; W _ЭГУ — передаточная функция электрогидравлического усилителя (ЭГУ); Δ p и Q — перепад давления и расход жидкости между рабочими полостями ЭГУ; K — коэффициент из формулы (33); S _п — эффективная площадь поршня силового гидроцилиндра; s — оператор Лапласа; С _о — коэффициент упругости места соединения основания корпуса силового гидроцилиндра рулевой машины (РМ) с рамой объекта управления; С_к — коэффициент упругости места соединения штока силового гидроцилиндра РМ с объектом управления; F _п.н — постоянно действующая нагрузка; m _н — масса объекта управления; Y _н — перемещение нагрузки; K _п.н — коэффициент позиционной нагрузки; K _о.с — коэффициент усиления сети обратной связи; T _о.с — постоянная времени фильтра в цепи обратной связи; Y _п и Y _ц — перемещение поршня и корпуса силового гидроцилиндра соответственно; F _с.т.н.д — сила сухого трения в нагрузке движения (рисунок создан автором)

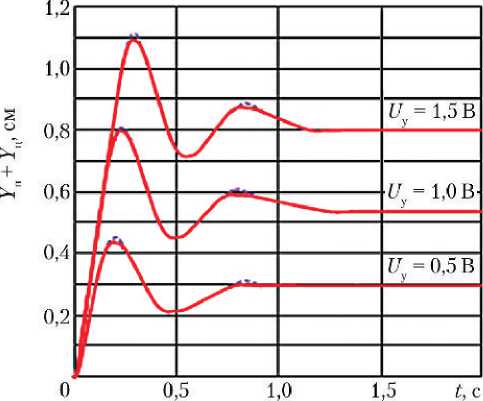
Рис. 8. Переходные характеристики рулевого тракта (РТ): Y _п + Y _ц — перемещение поршня и корпуса силового гидроцилиндра; t — время; U _у — управляющее напряжение на входе РТ; ^" — расчёт; ■ ■ ■ — эксперимент (рисунок создан автором)

Исследование влияния величины гидравлической силы, действующей на золотниковые плунжеры РМ с двухдроссельным ЭГУ, на переходную характеристику РТ и его устойчивость

Для исследования влияния величины гидравлической силы, действующей на золотниковые плунжеры статически устойчивой РМ с двухдроссельным ЭГУ [2], на переходную характеристику РТ и его устойчивость был проведён ряд вычислительных экспериментов с его полученной упрощённой математической моделью.

Эксперименты проводились путём введения множителя K перед выражением для гидравлической силы, действующей на золотниковые плунжеры ЭГУ РМ, т. е.

F _г = K spl( Q , Δ р ).

В процессе моделирования множителю K присваивались следующие значения: K = 1; K = 2; K = 5; K = 10.

Результаты вычислительных экспериментов представлены на рис. 9.

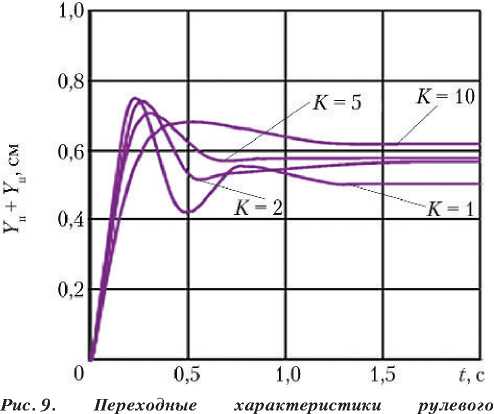
тракта при различных значениях множителя K: Y _п + Y _ц — перемещение поршня и корпуса силового гидроцилиндра; t — время; K — коэффициент из формулы (33) (рисунок создан автором)

Из графиков на рис. 9 следует, что величина гидравлической силы, действующей на золотниковые плунжеры ЭГУ статически устойчивой РМ, не влияет на динамическую устойчивость РТ, а только изменяет вид его переходной характеристики. Таким образом, увеличение гидравлической силы в статически устойчивой РМ не может приводить к автоколебаниям в РТ.

Заключение

Показана возможность создания упрощённой математической модели РТ СУВТ космического ракетного блока с применением аппроксимации нелинейных гидравлических характеристик двухдроссельного ЭГУ РМ методом многомерной кубической сплайн-интерполяции-экстраполяции.

Отличительная особенность разработанного метода заключается в том, что при математическом моделировании сложные аналитические зависимости характеристик не требуются, а для их аппроксимации в процессе расчётов используются только табличные представления экспериментальных данных.

Показано, что увеличение гидравлической силы в статически устойчивой РМ не может приводить к автоколебаниям в РТ, т. е. не влияет на его динамическую устойчивость, а только изменяет вид его переходной характеристики.