Создание модели квадрокоптера в среде MATLAB Simulink

Современные БПЛА (беспилотные летательные аппараты) бывают различных форм и размеров, но у всех у них есть один существенный недостаток: все они нуждаются в пилоте-операторе, управляющем дроном.

Целью работы является создание интеллектуальной системы автоматического управления БПЛА, способного работать в условиях чрезвычайных ситуаций.

Данная задача является комплексной. В ее состав входят:

• -    создание математической модели БПЛА;

• -    добавление механизмов самообучения и адаптации, создание робастной базы знаний;

• -    создание алгоритмов облета территории в условиях неоднородности окружающей среды, т.е. с учетом всевозможных препятствий, появляющихся на пути следования БПЛА;

• -    создание отказоустойчивого протокола коммуникации между группой дронов;

• -    реализация роевых алгоритмов для группы дронов для оптимизации задачи поиска на местности;

• -    интеграция системы распознавания образов для нахождения силуэта человека на местности.

Создание математической модели

Данную работу, в свою очередь, также можно разделить на части:

• -    создание математической модели полета дрона в виде системы дифференциальных уравнений;

• -    реализация данной системы уравнений в виде подсистемы в среде Matlab Simulink ;

• -    создание математической модели полета дрона в рамках теории управления (см. рис.1);

• -    интеграция Оптимизатора Баз Знаний на мягких вычислениях (далее ОБЗ) для настройки параметров ПИД-регулятора [1, 2];

• -    интеграция системы квантового нечеткого вывода [3].

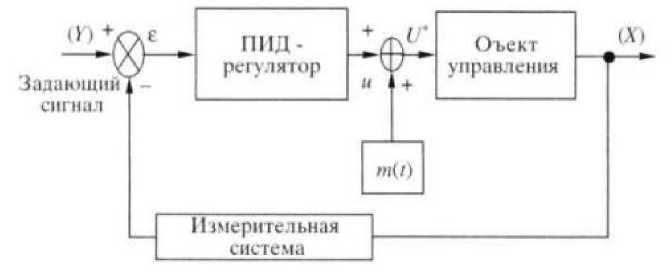
Рис. 1. Структура базовой системы управления

В данной публикации рассмотрены 1 -3 пункты.

В работе используется четырехвинтовой беспилотный летательный аппарат (далее - квадрокоптер). Выбор данного типа летательного средства определен относительной устойчивостью при всего четырех винтах.

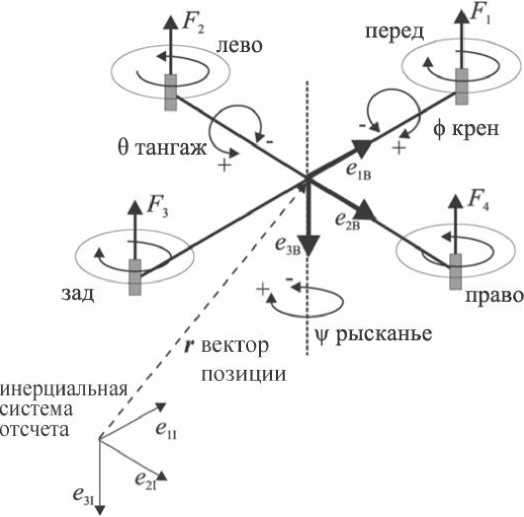
Рис. 2. Ориентация квадрокоптера в пространстве

Ориентация квадрокоптера в пространстве задается тремя углами, называемыми углами Эйлера-Крылова: рысканья - у , тангажа - 6 , крена - ф [4, 5, 6]. Они вместе составляют вектор:

QT = (фвy) .

Позиция устройства в инерциальной система отсчета задается радиус-вектором:

r T = ( xyz ) .

Матрица перехода из системы координат квадрокоптера в инерциальную систему координат имеет следующий вид:

( cos y cos в

R = sin y cos e

v - sin в

cos y sin в sin ф - sin y cos ф  cos y sin в cos ф + sin y sin ф ^

sin y sin в sin ф + cos y cos ф  sin y sin в cos ф - cos y sin y cose sin ф                   cos в cos ф         .

Сила тяги, производимая каждым из четырех двигателей равна:

F_t = b • О 2 .

Здесь ω i - угловая скорость двигателя, а b – коэффициент пропорциональности. Теперь мы можем записать дифференциальное уравнение, описывающее ускорение квадрокоптера по вертикальной оси [9]:

( 0 )

b ⁴

r = g • 0 - R • — У m"=

^o i

4, ,

Сразу же запишем второе дифференциальное уравнение:

I Q = -(Qx IQ) - MG + M

Здесь I – матрица инерции, M – вращающий момент, приложенный к квадрокоптеру, M G – гироскопический момент. Вектор M задается следующим образом:

(     Lb(^22 - ^42)

M =

Lb(^2 - ^32)

^d (^ + co^ - to^ - сОд)

Здесь d – коэффициент лобового сопротивления, L – длина плеча. Гироскопические моменты, вызванные поворотом объекта с вращающимися роторами двигателей:

M_G = I_R

GR

Qx

( 0 "

• (o - o + o - О).

Четыре сигнала управления, которые будут управлять квадрокоптером:

U = d О + o32 + of + of)u2 = b (o22 - of)

u3 = b(кф — ty2)

u^ — d ( 6 + t y₃

—

6 ^ 2 — 692)

.

В результате получена система уравнений, описывающая динамику полета квадрокоптера:

u x — —(cos фsm О cos^ + sin ф8Шф) • — m

u y — —(cos ф sin О sin ф + sin ф sin ф) • — m

z — g — (cos ф COS О ) • —

m

ф — Оф

x

—

IR- ° g ^{( U} ) ⁺ L^U 2

x

x

.

О — фф

—

I

IL

-R ф д ( u ) + — u I_y

I y

ф — Оф

⁺ yu 4

После того, как уравнения динамики системы будут записаны в виде системы Matlab Simulink , проверим ее на адекватность поведения. Для этого промоделируем поведение системы в состоянии равновесия (результат моделирования см. на рис. 3).

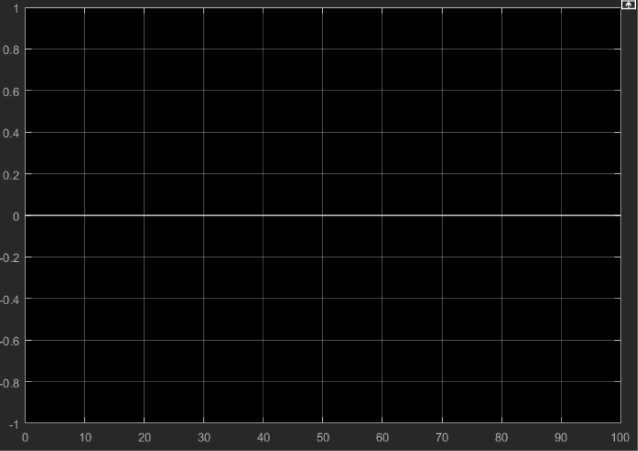
Рис. 3. Поведение системы в условиях нахождения в состоянии равновесия

Далее, промоделируем поведение системы, выведя ее из состояния равновесия (см. рис. 4).

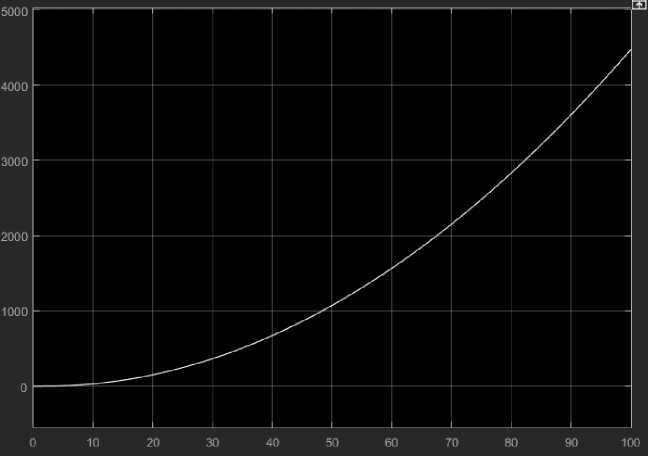
Рис. 4. Поведение системы вне состояния равновесия. Изменение длины вектора перемещения во времени

Как мы видим на рис. 3, система не изменяет своего состояния в течение времени находясь в устойчивом положении и при отсутствии влияния внешних сил. На рис. 4 видно, как система, при незначительном выводе из состояния равновесия и при отсутствии компенсирующих сил (чаще всего эту силу задает ПИД-регулятор) с течением времени стремится к бесконечности в пространственном отношении.

Данное поведение не имеет противоречий с поведением реального квадрокоптера в тех же условиях. На следующим шаге добавим в систему контур с обратной связью и ПИД-регулятор для формирования управляющего сигнала [8]. Промоделируем поведение системы, выведенной из состояния равновесия. Результаты продемонстрированы на рис. 5-8 для каждого из четырех двигателей соответственно.

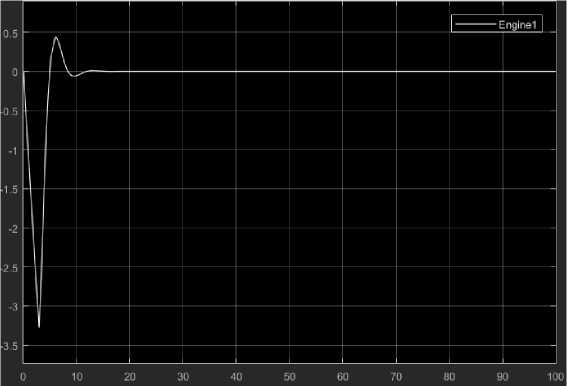
Рис. 5. Двигатель 1

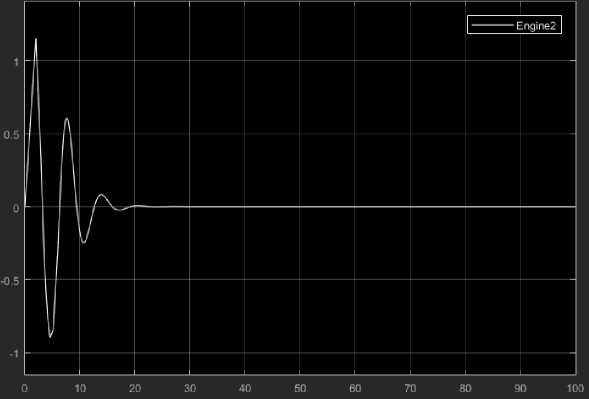
Рис. 6. Двигатель 2

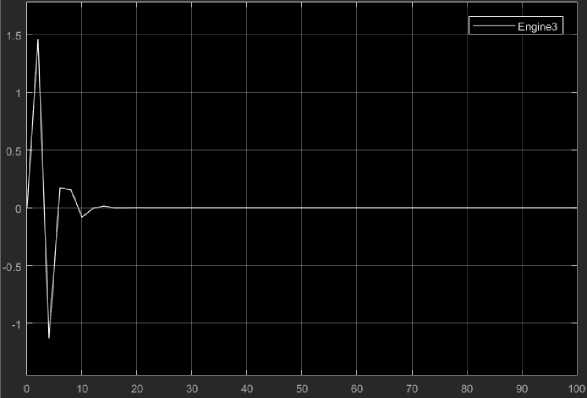
Рис. 7. Двигатель 3

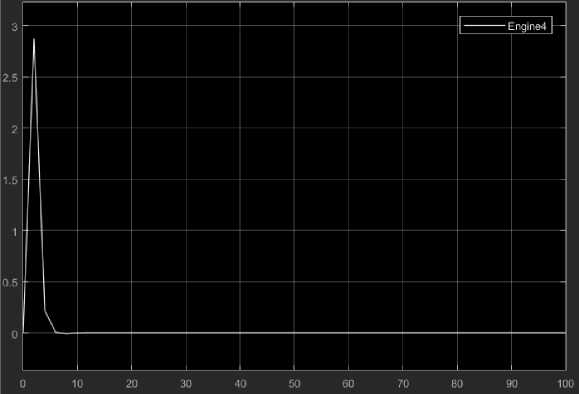
Рис. 8. Двигатель 4

Заключение

В работе получена математическая модель квадрокоптера. Поскольку система с ПИД-регулятором не обладает свойствами адаптации и обучения, то поведение системы корректно только при определенных, заранее предусмотренных условиях. Для достижения большей робастности системы следующим шагом должна быть интеграция Оптимизатора Баз Знаний [3, 4] для регулировки коэффициентов усиления ПИД-регуляторов.