Спасательные линеметы: математическое моделирование и экспериментальные исследования

Restech Norway представляет собой пусковое устройство, устанавливающееся на лафет, что в значительной степени снижает точность выстрела, а также увеличивает время на подготовку пуска [13].

Исследование процессов в момент выстрела важно для оптимизации конструкции (снижения максимального значения импульса отдачи, уменьшения габаритных размеров). Но на практике осуществить замеры необходимых параметров оказалось невозможным (время выстрела составляет не более 50 мс). Для описания процессов был создан экспериментальный стенд, а также проведено математическое моделирование динамики системы тел линемёта. Чтобы описать динамику, рассмотрим общий вид и принцип работы линеметательного устройства. В составе прибора (рис. 2) можно выделить корпус 1 , к которому прикреплена рукоятка 2 со спусковым крючком 3 . Корпус через казенник 4 соединен со стволом 5 . Баллон для сжатого воздуха с редукционным клапаном и манометром 6 установлен сверху и хомутами 7 прикреплен к корзине 8 , установленной на подвижной гильзе 9 . На конце гильзы установлен амортизатор 10 .

Рис. 1. Пусковое устройство линемета

Для того, чтобы привезти линемёт в рабочее состояние, нужно открыть вентиль баллона высокого давления, после чего воздух через редуктор начнет поступать в управляющую полость под колпак объемом V2, затем по кольцевому зазору в рабочую камеру –V3. При выстреле открывается запорный колпак клапана, и давление воздействует на снаряд, разгоняя его в стволе [11, 12]. Некоторая длина линя (равная длине ствола), укладывается в дно снаряда, а один конец закрепляется в казеннике линемёта. Разгон в стволе подчиняется законам внутренней баллистики, и можно считать перемещение контейнера как тела с постоянной массой. Поскольку время открытия клапана слишком малое (0,0005 с), то протекающие процессы можно считать адиабатическими и пренебречь эффектами газовой динамики. После того, как снаряд вылетает из ствола, срывается дно контейнера, и начинает разматываться линь, имеющий погонную массу ρ. Согласно рекомендации, выстрел следует производить пример- но под углом 30 градусов по отношению к самой высокой точке цели пуска.

Моделирование выстрела. Для рассмотрения проблемы динамики системы тел линемёта перейдем к расчетной модели (рис. 2).

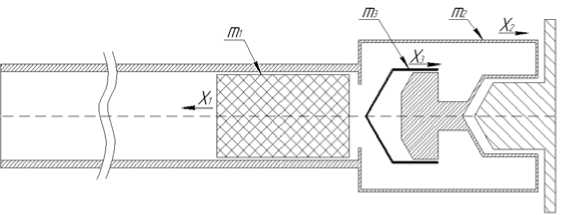
Рис. 2. Расчетная модель линемёта

В линемете имеем несколько движущихся тел: снаряд, пусковое устройство (ПУ) и колпак с массами m₁, m ₂, m ₃ соответственно. В снаряде уложен линь -нерастяжимая нить с погонной массой р и длиной 1 . Массы m₁ , m ₂ переменны из-за выхода линя из контейнера снаряда. Для описания движения эффективны уравнения Лагранжа 2-го рода [3, 7, 14]:

,д к ._D_ д к _    .xi

⁽-.)    - Qi .

д x i д x i         д x i

Обобщенные координаты xi – это абсолютные перемещения тел налево (x) и направо (x2, х3). Левые части уравнений (1) определяются выражением кинетической энергии

K = tm m₁ ( x ) x ? + m ₂ ( x ) x i + ^m ₃ x ₃² ],

m₁ = m ₁₀+p( 1 - x - x ₂), m ₂ = m ₂₀ +p( x₁ + x ₂)

где m ₁₀, m ₂₀ - массы снаряда и пускового устройства без линя. Вышедшая из контейнера снаряда часть линя считается неподвижной относительно ПУ.

В правых частях уравнений (1) – обобщенные силы с выделенными потенциальными слагаемыми. Для движения под действием только давления сжатого газа будем иметь Q i = 0, П = П( V ) — функция от объема газа. Потенциальную энергию П определим из следующих соотношений [3, 14]:

p0V0       _ дП   уY п = -1----V , p , pV = p0V0 ;

1 - у              д V                .      ⁽³⁾

V ( x ) = V + S ₁( x ₁ + x ₂) + S ₃( x ₃ - x ₂)

В геометрическое соотношение для объема V системы (3) входит начальный объем V 0 и площади сечения ствола S 1 и колпака S 3 . Формулы содержат давление p и соответствуют адиабатическому процессу с показателем у = 1.4 . Однако из-за отдачи при выстреле необходима опора – «плечо». Ей соответствует обобщенная сила со свойствами упругости и демпфирования. Положим

Q 2 =- cx 2 - bx^, Q 1 = Q 3 = 0          (4)

Приходим к следующей системе уравнений Лагранжа:

1 ,2

^m 1 ^x 1 ^- P⁽ - ^x 1 ^{+ x} 1 ^x 2 ) = Р^{( V} ) S 1 ,

3 2                                       (4)

m 2x2+P( 2 x 2- x x 2) = p(V)(S1+S3)+Q2, m 3x3 = - p (V) S3

где объем V определяется выражением (3). Система нелинейная, шестого порядка. При заданных начальных условиях она интегрируется средствами компьютерной математики [6]. При этом вводим скорости v_t = xj и получаем шесть уравнений.

На рис. 3 представлены функции x i ( t ) - результаты численного интегрирования с встроенной функцией rkfixed [6]. Значения параметров: m ₁₀ = 0.508 кг, р = 1.13 - 10 ^-3 кг/м, m ₂₀ = 7.07 кг, m ₃ = 0.008 кг, S ₁ = 0.002 м ² , S 3 = 0.001 м ² , V ₀ = 0.562 - 10 ^{- 3} м ³ , 1 = 260 м, c = 100 Н/м, b = 100 Н • с/м. Законы изменения координат с большой точностью соответствуют равноускоренному движению – ускорения не успевают измениться на рассматриваемом начальном этапе.

Моделируемый первый этап процесса заканчивается соударением колпака с направляющей в некоторый момент времени t1 . При этом выполняется условие x3< t1) - x2< t1) = А,      (5)

где А = 0.008 мм - заданный начальный зазор. Из уравнения (5) численно определяется время t₁ = 1.46 • 10 ^{- 4} с. Графики на рис. 3 построены в более широком интервале.

Далее начинается второй этап процесса выстрела. Колпак и пусковое устройство составляют одно целое, координата x3 как независимая исчезает, количество уравнений Лагранжа уменьшается до двух. Начальные условия определяются значениями координат и скоростей в конце первого этапа. Численное интегрирование не вызывает проблем. Заканчивается этап вылетом снаряда из ствола в момент времени t2 с выполнением условия x1( 12) + x 2( 12) = L       (6)

( L = 0.75 м - длина ствола).

Последний третий этап – полет в пространстве. Его нетрудно моделировать, только если пренебречь силой тяжести [10]. Иначе необходимо вводить дополнительные координаты по вертикали, учитывать изгиб линя, а также сопротивление воздуха. Это выходит за рамки данной статьи. Важнейшей расчетной величи- ной является скорость соударения колпака клапана линемета (КК) с направляющей пускового устройства *

v = v3(t1)-v2(t1) = 108.9 м/с (7)

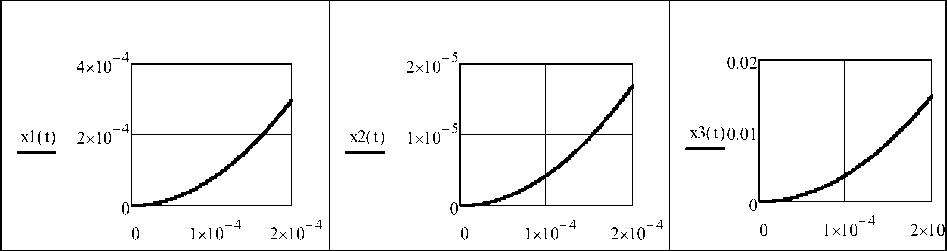
Рис. 3. Зависимость перемещений тел от времени

Расчет этой величины важен для прогнозирования прочности КК [1]. При испытаниях и эксплуатации линемета были случаи разрушения КК. Поэтому проводились поиски особых прочных материалов для КК. Специально для клапана был выбран композиционный материал Хостаформ С27021 с полиформальдегидной матрицей и включениями в виде микросфер [8, 9].

Испытательный стенд. Для экспериментального исследования процессов в линемёте был создан испытательный стенд (рис. 4) [4, 5]. Рассмотрим схему стенда (рис. 5). На ней можно отметить следующие составляющие: 1 – рабочая камера высокого давления; 2 – баллон высокого давления; 3 – пусковой клапан и ПЭК; 4 – запорный элемент (колпак); 5 – ствол; 6 – измеритель скорости пролетного типа (а - первый оптический датчик, б - второй оптический датчик); 7 – уловитель снарядов [16, 17]. Аналоговые датчики давления (II,III,IV) – линейного типа; они соединены с аналогоцифровым преобразователем. Сигналы с него поступают на устройство вывода, обрабатываются, и выдаются в виде графиков. Цифровой датчик высокого давления (I) подключен непосредственно к рабочей камере линемёта и показывает давление в ней.

Рис. 4. Внешний вид испытательного стенда

Работу испытательного стенда можно разделить не несколько последовательных процессов:

• 1.    подача электрического сигнала на катушку ПЭК;

• 2.    перемещение штока ПЭК - подача воздуха на сбросовый клапан;

• 3.    открытие сбросового клапана;

• 4.    сброс воздуха из-под колпака основного клапана – срабатывание основного клапана линемёта;

• 5.    разгон снаряда в стволе;

• 6.    выход снаряда со среза ствола;

• 7.    попадание в уловитель.

После накачивания рабочей камеры и подвода магистрали промышленного давления к пусковому клапану система готова к пуску. Началом отсчета всех процессов является подача электрического сигнала на катушку ПЭК и его запуск. После переключения рабочих полостей распределителя происходит запуск пускового клапана, который открывает сбросовое отверстие полости, соединенной с основным клапаном ли-немёта. Система начинает сбрасывать воздух из-под колпака. В определенный момент, когда давление под колпаком становится примерно в 3 раза меньше рабочего давления, происходит открытие клапана линемё-та, снаряд приобретает импульс и начинает двигаться по стволу [18, 19]. При пролете над измерителем скорости первый и второй оптический датчики фиксируют изменение светового потока, и происходит замер скорости, отражающийся на дисплее. Затем снаряд тормозится уловителем, который представляет собой трубу длиной 1.3 м с толщиной стенки 12 мм, наполненную внутри демпфирующим материалом.

Один из результатов эксперимента: время импульса отдачи, который воздействует на плечо стрелка, напрямую зависит от времени разгона снаряда в стволе. Сократить время можно уменьшением длины ствола. Однако длину ствола можно уменьшать до определенных размеров, чтобы был обеспечен заброс снаряда на нужную длину. По показаниям датчиков II и IV было определено время разгона снаряда в стволе. Экспериментальные данные приведены в табл. 1.

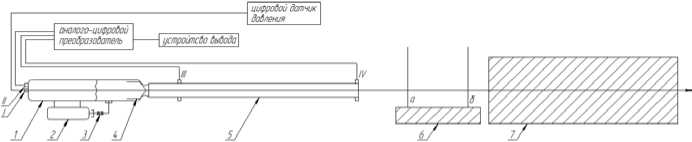
Рис. 5. Схема испытательного стенда

Таблица 1. Время разгона снаряда в стволе

№	1	2	3	4	5	6	7	8	9	10	11
Р, Мпа	1	1,5	2	2,5	3	3,5	4	4,5	5	5,5	6
t, мс	31	23	22	20	18	17	16	15	14	13	13

Скорость на срезе ствола определялась специальным прибором – измерителем скорости пролетного типа, по оптическим датчикам. Результаты приведены в виде графика на рис. 6.

Выводы: рассмотрена конструкция и принцип линемёта ИСТА-240, с помощью уравнений Лагранжа смоделирован выстрел спасательным снарядом и описана динамика системы трех тел. С помощью средств компьютерной математики получены зависимости перемещений тел от времени. Вычислен важный параметр – скорость колпака в момент соударения. Данное значение позволит оптимизировать конструкцию, а также избежать механического разрушения. Сконструирован новый испытательный стенд, на котором получены такие характеристики как – время разгона снаряда в стволе и скорость на срезе ствола.

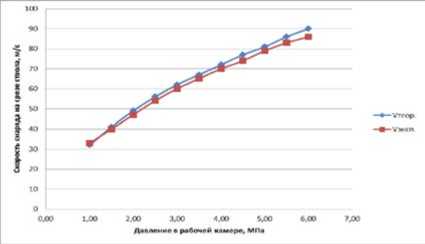
Рис. 6. График зависимости скорости снаряда на срезе ствола от давления в рабочей камере

Работа выполнена в рамках государственного задания при финансовой поддержке Минобрнауки России. Коды проектов: № 933-2014, № 1972-2014.