Spatial and Transform Domain Filtering Method for Image De-noising: A Review

Published Online September 2013 in MECS

Filters play a significant role in the image de-noising process. It is a technique for modifying or enhancing an image. There are two basic approaches to image denoising, spatial filtering methods and transform domain filtering methods. A traditional way to remove noise from image data is toemploy spatial filters. Spatial filters can be further classified into non-linear and linear filters Error! Reference source not found..

• A.    Median Filter

Spatial filters employ a low pass filtering on groups of pixels with the assumption that the noise occupies the higher region of frequency spectrum. Generally spatial filters remove noise to a reasonable extent but at the cost of blurring images which in turn makes the edges in pictures invisible. With non-linear filters, the noise is removed without any attempts to explicitly identify it like median filter. Median filter follows the moving window principle, like mean filter. A 3×3, 5×5, or 7×7 kernel of pixels is moved over the entire image.

B(1,1)	B(1,2)	B(1,3)
B(2,1)	B(2,2)

Figure 1.Processed Neighbors

First the median of the pixel values in the window is computed, and then the center pixel of the window is replaced with the computed median value. Calculation of Median is done as first sorting all the pixel values from the surrounding neighborhood (either ascending or descending order) and then replacing the pixel being considered with the middle pixel value. Median filter works as shown in “(1)”.

/(x,y)=median (s,t) _i sxy {g(s,t)}                             (1)

• B.    Weiner Filter

Linear filters too tend to blur sharp edges, destroy lines and other fine image details, and perform poorly in the presence of signal-dependent noise, like weiner filter.Wiener filter is based on the least-squared principle, i.e. the filter minimizes the mean-squared error (MSE) between the actual output and the desired output. Wiener filtering is given by “(2)”.

a ?

f (x,y)=g + 1—^ (g(x, y) - g )                   (2)

" f ^-a A

Where f (x,y) denotes the restored image and gisthe local mean of is local variance о,is the noise variance

Let us consider (2m+1)×(2n+1) window size then local mean g is defined as in “(3)”.

5=1 Z™-_mZt₌-_nS G, t)                            ⁽³⁾

Where L is total number of pixels in a window .Similarly consider (2m+1)*(2n+1) window then local variance ag is defined as in “(4)”.

о/ = 7-7ST=-_m S?=—„ {a⁽s , t) - gy               (4)

• ⁵ L —1

The local signal variance af is used in “(2)” is calculated from ag with a priori knowledge of noise variance a_n² simply by substracting a2 from ag with the assumption that signal and noise are not correlated with each other.

The transform domain filtering methods can be subdivided according to the choice of the basis functions. The basis functions can be further classified as data adaptive and non-adaptive.

• C.    Wavelet Denoising

The non-data adaptive transform domain method such as discrete wavelet transform contains the methodology of image de-noising that follows in three steps as summarized below:

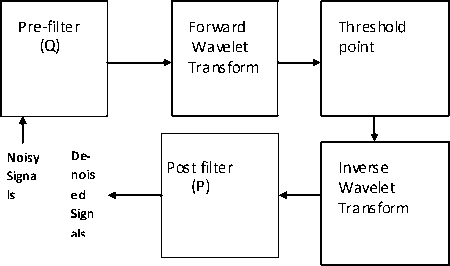
• 1.    Transform the noisy image into orthogonal domain by 2D discrete wavelet transform as given in “(5)”.

• 2.    Apply hard or soft thresholding to the noisy detail coefficients of the wavelet transform.

• 3.    Perform inverse discrete wavelet transform to obtain the de-noised image as in “(6)”.

^sdwt ^(j, k) = ^=1 S_nj _kw_n                         (5)

Where a = 2 j , τ =k2 j sn= s(nT) Signal samples

W = nth sample of kth shifted version jk n nth of a 2j scaled discrete wavelet.

N= number of signal samples

s„ =¹ № ^N Y' ⁽ ₀ ^N/2+1) Sj _k W .               (6)

^ri N j =0 k = 0             j >^K jk n                             ^x '

Where ^{jkWn = n} sample of kth sifted version of a 2j scaled discrete wavelet.

J,k = row index.

n = column index.

Here, the threshold plays an important role in the denoising process. Finding an optimum threshold is a tedious process. A small threshold value will retain the noisy coefficients whereas a large threshold value leads to the loss of coefficients that carry image signal details.

• D.    Independent Component Analysis

Whereas data adaptive transform domain filtering method such as ICA is widely used in image de-noising in ICA transform data is represented as it can be define the ICA as it is a random vector X consists of finding a linear transform as in “(7)”.

X=AS                                     (7)

So that the components si are as independent as possible, with respect to some maximum function that measures independence. This definition is known as a general definition where no assumptions on the data are made. Independent component analysis (ICA) is the decomposition of random vector in linear components which are “as independent as possible”. Here, ’independence’ should be understood in its strong statistical sense: it goes beyond second order decorrelation and thus involves the non-gaussianity of the data. The ideal measure of independence is the higher order cumulates like kurtosis and mutual information.

In addition to the basic assumption of statistically independence, by imposing the following fundamental restrictions, the noise free ICA model can be defined if.

• 1.    All the independent components Si, with the possible exemption of one component, must be non-Gaussian

• 2.    The number of observed linear mixtures m must be at least as large as the number of independent components n;

• 3. The matrix A must be of full column rank

i.e. m> p

We can invert the mixing matrix as in “(8)”

S = A-1 X                                         (8)

Thus to estimate one of the independent components, we can consider a linear combination of Xi Let us denote this by “(9)”

Y= bTX= bTAS                              (9)

Hence if b were one of the rows of A-1, this linear combination bTXwould actually equal one of the independent components. But in practice we cannot determine such ‘b’ exactly because we have no knowledge of matrix A, but we can find an estimator that gives a good approximation.

• II.    LITERATURE REVIEW

Digital image processing has many significant advantages over analog image processing. Image processing allows a much wider range of algorithms to be applied to the input data and can avoid Problems such as the build-up of noise and signal distortion during processing of images.

Four types of noise (Gaussian noise , Salt and pepper noise, Speckle noise and Poisson noise) has taken and image de-noising performed for different noise by Mean filter, Median filter and Wiener filter[2] .Suryanarayana et.al.suggested a simple noise (Salt and pepper) detection technique by using 3x3 sub-windows in which the test pixel appears. A weight is assigned to the test pixel based on its position after sorting in each subwindow. Two thresholds are used to decide whether the test pixel is corrupted or not. If corrupted then only the standard median of the 3 x 3 vicinity is used to eliminate noise, otherwise no filtering is applied[3].Chang C.C. et.al emphasizeon a new image-de-noising filter that is based on the standard median (SM) filter in which a threshold and the standard median is used to detect noise and change the original pixel value to a newer that is closer to or the same as the standard median. Authors also incorporated the center weighted median (CWM) filter[4]. Authors focused on comparative study of image de-noising techniques relying on spatial filters. Subjective and objective evaluation methods are used for judging the efficiency of different types of spatial filters applied to different types of noise. Moreover, authors proposed de-noising technique that is based on cascaded median and wavelets filter[5]Image is usually corrupted by two or more different type of noise simultaneously, so Gui-quanet.al. proposed a new mixture filter method in which they classified the pixels into two classes, one is the pixels which are corrupted by impulse noise and the other is the pixels corrupted by Gauss noise. Then median filter is used for the pixels corrupted by impulse noise and wavelet threshold method filter is used for the pixels corrupted by Gauss noise[6]. Jiang J.and Shen J. focused on effective adaptive median filter algorithm for removing salt and pepper noise in images. It has also solved the problem of the simplified Pulse Coupled Neural Network model in image filtering. At first, the simplified model is proved to fail to detect pepper noise using the method of reduction and then the model is improved using the method of divide and rule, finally, the adaptive median filter algorithm is achieved by detecting the pollution level of the image, ascertaining the specific location of the noise and determining the size of the median filtering window adaptively[7]. In real applications, different regions in the image will often be corrupted by different noise. So Qiu Yet.al. discussed this problem and proposed an adaptive image de-noising method for mixture Gaussian noise in an image. There are two phases in this proposed method: noise estimation and noise removal. Here authors applied high pass filter using two order differences to estimate different noise standard deviations in different regions.Then authors divided the filtered image into a number of blocks and computed the histogram of all the block’s standard deviations. An averaging over the peak will estimate the noise standard deviation in one region. Finally, they combined data fusion with an existent de-noising method to remove noise[8].RatnaBabu K. et.al.proposed a De-noising algorithm to perform image de-noising which eliminates salt and pepper noise. Authors used a method that is better in suppressing salt and pepper noise at different noise levels and preserve fine details in the image while removing the noise[9]. Authors proposed a methodology of image de-noising which is based on median filter and wavelet theory, for removing additive salt and pepper noise or white Gaussian noise. In the first phase, Canny edge detection is used in edge detection of the noise image to get the basic outline; In the second phase, an ameliorative adaptive median filter(adaptive variational threshold value) is used to remove salt noise; In the third phase, Coiflet wavelet system used to remove pepper noise; at last, processing images linking to get final images[10].In this paper it has been tried to remove the various noise(Gaussian, speckle, salt n pepper noise) by using the filters as individual median filter and only the wavelet filter and then we have applied the cascaded form of median and wavelet transform filter to remove the noise up to great extent[11].

Selesnick I.W.described a new complex-directional expansive perfect reconstruction two-dimensional wavelet transform.The transform is based both on the complex dual-tree wavelet transform and on the doubledensity DWT. It is designed so as to possess simultaneously the properties of the complex dual tree DWT and the double density DW T[12] .

Method for removing Poisson noise from a degraded image in wavelet domain has been proposed in [13]. This methodwidens the conventional BayesShrink approach and is operated by processing not only detail coefficients (Wavelet coefficients) but also the coefficients related to the rough approximation (Approximation coefficients). In order to remove the large-amplitude noise which cannot be removed by conventional wavelet shrink methods, authors proposed a new type of directional adaptive center weighted median filter (DACWMF). In this paper authors proposed the improved performance and computational speed of the wavelet shrinkage algorithm and experimentally compared with established methods. The de-noising method incorporated in the proposed algorithm involves a two-threshold validation process for real-time selection of wavelet coefficients. The proposed algorithm takes image features into consideration in the selection process. Therefore, two thresholds are used in the coefficient selection process. The first threshold is used to distinguish coefficients of large magnitude and the second is used to distinguish coefficients of spatial regularity [14].In this paper authors proposed an improvement to an adaptive threshold estimation method for image de-noising in the Wavelet domain. The proposed methods have required the parameters for estimating the threshold depend on sub band data. The threshold is computed by [βσ2 / σy] whereσ2 and σy are the standard deviation of the noise and the sub band data of noisy image respectively. β is the scale parameter, which depends upon the sub band size and number of decompositions[15]. In the paper, an algorithm based on Dual-Tree Complex Wavelet Transform is proposed by authors for 1/ f process denoising. Authors used the variance of the wavelet coefficients at different scales to estimate the parameters [16].In this paper author presented conditions under which the sampling lattice for a filter bank can be replaced without loss of perfect reconstruction. The results provided a simple way of building oversampled filter banks. If the original filter banks are orthogonal, these oversampled banks construct tight frames of 2( ) when iterated. The frame transform is nearly shifting invariant and has intermediate scales[17].

In this paper, authors emphasized on a novel image de-noising algorithm that incorporates the dual-tree complex wavelets into the ordinary ridgelet transform. The approximate shift invariant property of the dual-tree complex wavelet and the high directional sensitivity of the ridgelet transform make the new method a very good choice for image de-noising. Author applies the digital complex ridgelet transform to the de-noising of some standard images embedded in white noise. A simple hard thresholding of the complex ridgelet coefficients is used [18]. In this paper, authors focused on a method to design image-matched bi-orthogonal wavelet bases and report on their potential for de-noising. He has conducted experiments on various image datasets namely Natural, Satellite and Medical with the designed wavelets using two existing thresholding strategies. Test results from comparing the performance of matched and fixed bi-orthogonal wavelets show an average improvement of 35% in MSE for low SNR values (0 to 18db) in every dataset[19]. Authors described a computationally more efficient and adaptive threshold estimation method for image de-noising in the stationary wavelet domain. In this proposed method, the choice of the threshold estimation is carried out by analyzing the statistical parameters of the wavelet sub band coefficients like standard deviation, arithmetic mean and geometrical mean. Then novel threshold method is used to remove the noisy coefficients, by combing the soft-thresholding and hard-thresholding by the proposed method [20]. In this paper authors presented a new image de-noising method. Firstly, this method decomposed the noisy image in order to get different sub-band image. Secondly, they remained the low-frequency wavelet coefficients unchanged, and after taking into account the relation of horizontal, vertical and diagonal high-frequency wavelet coefficients and comparing them with Donoho threshold, they made them enlarge and narrow relatively. Thirdly, they used soft-threshold de-noising method to achieve image de- noising. Finally, they got thede-noising image by inverse wavelet transform [21].In this paper, authors proposed an adaptive method of image de-noising in the wavelet sub band domain. This approach is based on threshold estimation for each sub band of the wavelet decomposition of a noise-contaminated image, by considering that the sub band coefficients have a Generalized Gaussian Distribution (GGD). Under this framework, the proposed technique estimates the threshold level by applying a robust median estimator on either all the detail coefficients or every detail sub band of each decomposition level[22]. In This paper authors proposed an adaptive threshold estimation method for image de-noising in the wavelet domain based on the generalized Gaussian distribution (GGD) modeling of sub band coefficients. The proposed method called Normal Shrink is computationally more efficient and adaptive because the parameters required for estimating the threshold depend on sub band data. Author done Experimental results on several test images are compared with various de-noising techniques like Wiener Filtering, Bayes Shrink and Sure Shrink[23]. In this paper, authors presented a modified structure that enables the utilization of an unlimited number of wavelet filters. An alternative de-noising technique is thus proposed with a simple approach for the utilization of multiple wavelet filters. According to the probability distribution function associated with each sub band of the transformed data, different de-noising methods are adaptively applied. The proposed expansion is based on the use of either a Walsh-Hadamard Transform (WHT) or independent component analysis (ICA) to remove dependencies between the data streams associated with each wavelet decomposition[24]. In this paper author focused on a wavelet-based thresholding scheme for noise suppression in ultrasound images. Quantitative and qualitative comparisons of the results obtained by the proposed method with the results achieved from the other speckle noise reduction techniques demonstrate its higher performance for speckle reduction[25]. In order to sharpen image details and reducing noise, based on the multi-analysis wavelet threshold de-noising method, a Labeling-based block-matching and wavelet transform filtering method combine hard and soft threshold denoising approaches (BWHS) is proposed by author in this paper. First, they estimated the noise variance of image. Second computed the matching blocks, and constructed the 3D data array of those similar blocks, the high and low frequency sub-bands de-noised by the best soft threshold, hard threshold that result from the iterative calculation of noise variance respectively, Finally, sharpen image details using DC coefficients of LL frequency sub-bands[26] . In this paper Shuang-ping Z. presented a combined de-noising method based on an adaptive Wiener filtering in the wavelet domain and an adaptive Wiener filter in the spatial domain. First a predenoised image is obtained with the thresholdingde-noising in the wavelet domain and the residual noise variance of that is re-estimated. Then an adaptive Wiener filtering in spatial domain is applied to the reconstructed image to improve the accuracy[27]. Authors proposed a method for image de-noising in the filter domain based on the Characteristics of the Empirical Mode Decomposition (EMD) and the wavelet technique. The proposed method uses the EMD to the decomposition and double density wavelet to filter components [28]. In This paper authors emphasized on different approaches of wavelet based image de-noising methods. Multi wavelets can be considered as an extension of scalar wavelets. The main aim of the authors is to modify the wavelet coefficients in the new basis, the noise can be removed from the data. In this paper, they extended the existing technique and provided a comprehensive evaluation of the proposed method [29]. In this paper authors focused on a new wavelet transform applicable to functions defined on high dimensional data, weighted graphs and networks. The proposed method generalizes the Haar-like transform recently introduced by Gavish et al., and can also construct data adaptive orthonormal wavelets beyond Haar. It is defined via a hierarchical tree, which is assumed to capture the geometry and structure of the input data, and is applied to the data using a modified version of the common one-dimensional (1D) wavelet filtering and decimation scheme [30]. In this article authors stated a statistically optimum adaptive wavelet packet thresholding function for image de-noising based on the Generalized Gaussian Distribution (GGD). It applies computationally efficient multi-level wavelet packet decomposition to noisy images to obtain the best tree or optimal wavelet basis utilizing Shannon entropy. They selected an adaptive threshold value which is level and sub band dependent based on analyzing the statistical parameters of sub band coefficients. In the utilized thresholding function, which is based on maximum a posteriori (MAP) estimate, the modified version of dominant coefficients was estimated by optimal linear interpolation between each coefficient and the mean value of the corresponding sub band[31]. In this work, authors proposed a fast alternative to iterative Gaussianization methods that makes it suitable for image processing while ensuring its theoretical convergence[32]. Author performed a comparison between two source signal extraction algorithms, namely the Wavelet De-noising (WD) by Soft Thresholding and Independent Component Analysis (ICA) on a simulated functional optical imaging data. The simulated data are generated by combining a gamma function superimposed on a very low frequency sine wave as the source data and the additive noise components are chosen as having both Gaussian and non-Gaussian parts[33]. In this work, authors compared the effect of different de-noising filters acting on digitized mammograms. The considered filters are: a local Wiener filter, a wavelet filter, a filter based on independent component analysis, and finally, a filter based on the diffusion equation[34]. The basic model of independent component analysis is introduced by authors in this paper. The ICA of noisy signal is discussed. The technique of wavelet thresholdingde- noising and the algorithm of FAST ICA are both studied with computer simulation of noisy image separation[35]. Authors stated ade-noising algorithm for enhancing noisy signals based on local independent component analysis (ICA). This is done by applying ICA to the signal in localized delayed coordinates. The components resembling the signals can the detected by various criteria depending on the nature of the signal. Estimators of kurtosis or the variance of the autocorrelation have been considered. The algorithm proposed can favorably be applied to the problem of de-noising multidimensional data like images or fMRI data sets [36]. In this paper, Yu Y. and Yang J. showed how to choose the optimal sparse coding basis for de-noising and how to apply an improved shrinkage operation on the components of sparse coding so as to reduce noise [37]. Authors described a new method for blind source separation, adapted to the case of sources having different morphologies. They showed that such morphological diversity leads to a new and very efficient separation method, even in the presence of noise. The algorithm is called MMCA (Multichannel Morphological Component Analysis), is an extension of the Morphological Component Analysis method (MCA). MCA has been shown to be an efficient technique in such problems as separating an image into texture and piecewise smooth parts or for in painting applications. The proposed extension, MMCA, extends the above for multichannel data, achieving a better source separation in those circumstances [38]. In this paper, authors introduced independent component analysis (ICA), a simple, efficient and applied method to clean image noise. Independent component analysis is a method in which the goal is to find a linear representation of nonGaussian data so that the components are statistically independent, or as independent as possible. Such a representation seems to capture the essential structure of the data in many applications, including feature extraction and noise cleaning of an image [39]. In the present paper authors deal with a set of images that are mixed randomly. They applied the principle of uncorrelatedness and minimum entropy to find ICA. The original images are then retrieved using fixed point algorithm known as FastICA algorithm and compared with the original images with the help of estimated error. The outputs from the intermediate steps of algorithm such as PCA, Whitening matrix, Convergence of algorithm and de-whitening matrix are also discussed [40]. In this paper, authors proposed a single channel image de-noising algorithm by constructing a noise image to as another observation signal for single channel noise reduction based on independent component analysis, thereby noise and original image can be separated through independent component analysis [41]. A new natural image de-noising method using Sparse Independent Component Analysis (SICA) based on Gabor wavelet is discussed in this paper by authors. In order to maximize the sparsity, SICA algorithm utilized as the sparse function. At the same time, to insure the speed of SICA, 2-D Gabor wavelet bases are used as the initialization feature bases of SICA. This SICA algorithm does not need optimizing the high order non-linear functions and density estimation, therefore, it is very simple in computing and its convergent speed is also very quick[42]. Independent component analysis (ICA) is a new method of blind source separation. A method of image de-noising based on ICA is presented in this article by author .It can separate noisy mixed images effectively. The principle of ICA and Fast ICA algorithm based on negentropy criterion are introduced [43]. In this paper, authors proposed de-noising of microarray images using the independent component analysis (ICA). The idea of ICA i.e. finding the linear representation of nongaussian data so that the components are independent (or at least as independent as possible) is exploited for de-noising microarray images[44]. In This paper authors reviewed significant existing de-noising methods based on Independent Component Analysis and concludes with the tabular Summary of de-noising methods and their salient features / applications [45].

In this paper, ICA has been used to separate out noise from the image to provide important diagnostic information to the physician and its usefulness is demonstrated by comparing its performance with other noise filtering methods. The performance of the ICA and other de-noising techniques is evaluated using the metrics like Peak Signal-to-Noise Ratio (PSNR), Mean Absolute Error (MAE) and Mean Structural Similarity Index (MSSIM)[46]. In this paper a hybrid Wavelet-ICA method for improving the functionality of noise free ICA algorithm in noise environment is proposed by authors .At first the robustness of the two frequent ICA algorithm named fast ICA and information maximization ICA for extracting true activated spatial and temporal sources of FMRI signals in presence of different noise levels are evaluated. These algorithms are applied on simulated FMRI dataset consisting of different activated sources with various temporal pattern, different level of activation, trend and noise. Then a hybrid wavelet-Fast ICA model to transform the signals into a domain, allowing for simultaneous un-mixing and wavelet basedde-noising is proposed [47].In This paper authors presented a novel adaptive method of image denoising based on the dual-tree complex wavelet transform (DTCWT) and independent component analysis (ICA). This method extracted the high-frequency component of the image with the DTCWT, then combining with the principle of ICA virtual observed noise channel de-noise. Moreover, it overcomes the deficiency in wavelet threshold denoising, that is the selective and the quantitive of threshold[48]. Authors proposed an automatic method for artifact removal and noise elimination from scalp electroencephalogram recordings (EEG). The method is based on blind source separation (BSS) and supervised classification and proposed a combination of classical and news features and classes to improve artifactelimination (ocular, high frequency muscle and ECG artifacts). The role of a supplementary step of wavelet de-noising (WD) is explored and the interactions between BSS, de-noising and classification are analyzed [49]. In this paper authors used Spatially-Constrained Independent Component Analysis (SCICA) to separate the Independent Components (ICs) from the initial EEG signal. As the next step, Wavelet De-noising (WD) is applied to extract the brain activity from purged artifacts, and finally the artifacts are projected back and subtracted from EEG signals to get clean EEG data. Here, thresholding plays an important role in delineating the artifacts and hence a better thresholding technique called Otsu’, thresholding is applied [50]. In this paper authors presented a new algorithm using a merger of Independent Component Analysis and Translation Invariant Wavelet Transform. The efficacy of this algorithm is evaluated by applying contaminated EEG signals. Its performance was compared to three fixed-point ICA algorithms (FastICA, EFICA and Pearson-ICA) using Mean Square Error (MSE), Peak Signal to Noise Ratio (PSNR), Signal to Distortion Ratio (SDR), and Amari Performance Index [51]. In this paper we have tried to remove the noise in MRI images by using the cascaded form of ICA and wavelet transform domain method [52].

• III.    CONCLUSION

A large number of linear and non linear filtering algorithms have been developed to reduce noise from corrupted images to enhance image quality. The most common type of noise is the white or Gaussian noise where its power is uniformly distributed over the spectral and spatial spaces and its mean is zero. Linear filtering is an efficient technique to deal with additive noise while non-linear filters are efficient to deal with the multiplicative and function based noise. If we are moving to the transform domain method then non adaptive basis function based wavelet transform domain method provides better de-noising while preserving the details of image like edges.

The main assets of the wavelet transform are:

• 1.    The ability to compact most of the signal’s energy into afew transformation coefficients, which is called energy compaction.

• 2.    The ability to capture and represent effectively low frequency components (such as image backgrounds) as well as high frequency transients (such as image edges).

• 3.    The variable resolution decomposition with almost uncorrelated coefficients.

• 4.    The ability of a progressive transmission, which facilitates the reception of an image at different qualities.

Data adaptive basis function based method like independent component analysis is a higher order statistical method suitable for multidimensional and multivariate data analysis and processing. De-noising of natural images by ICA methods are strongly data adaptive as de-noising processes do not require the noise free image in general, which is the uniqueness of this method that makes it more efficient than wavelet and other transform domain filtering methods. This review concludes that filtering method that includes cascading methods i.e. one filtering method followed by another filtering method performs better. There is a conflict between filtering method which should be applied first ,for example if we are discussing between wavelet transform (to eliminate additive noise) and ICA(to indentifyartifact sources),then if there is no noise then source separation method will perform better but if there is noise then our approach will be to denoise the signal before applying ICA. On the other hand wavelet transform may cause loss of information during de-noising that may be useful for ICA and for classification purpose. We can conclude that type of used filter will vary according to the type of noises added in the image.