Специальные асимптотики функций параболического цилиндра (функций Вебера - Эрмита) с большим параметром

Функции параболического цилиндра (функции Вебера – Эрмита) с большим параметром вида

D va ( x ) = J exp { i л ( 1 2 + tx ) } • t i ^Av • tdt                         (1)

Y возникают при рассмотрении решений задач квантовой физики, волновых уравнений электродинамики неоднородных сред и других задачах, связанных с нахождением приближенных решений на основе имеющейся информации о соотношении характерных масштабов вариации переменных коэффициентов уравнений и масштабов изменения самого решения. Данное соотношение характеризует параметр Л, пропорциональный отношению этих масштабов.

Представление функций параболического цилиндра в форме (1) выделяет в явном виде специальный вид зависимости от большого параметра Л и формально отличается от классических интегральных представлений лишь масштабированием переменной t (в комплексной плоскости контура γ) и, соответственно, переменных x и ν [1–3]. Однако при рассмотрении асимптотических разложений (при Л >>  1 ) присутствие большого параметра во внеэкспоненциальной части интегрального представления

(1), или, что эквивалентно, в логарифмическом члене «фазовой функции» (см. ниже), существенно отличает данное интегральное представление от других интегралов с большим параметром [4–7].

Важным вопросом при анализе выражений такого рода является корректное построение асимптотических разложений интеграла (1) по параметру Л^{- 1} ( Л >>  1 ) , равномерных по x и ν. В зависимости от значений переменных x и ν можно выделить области с различным видом асимптотик, оценивающих функцию (1). Такие асимптотики, как неравномерные, не затрагивающие особенности интеграла (1), так и равномерные, учитывающие особенности в выделенных областях, соответствуют специфической структуре особенностей интеграла (1) и отражают не только математическую суть проблемы, но и дают корректную интерпретацию решений, содержащих функции параболического цилиндра, для многих прикладных задач. Присутствие большого параметра при аргументе ν требует рассмотрения в качестве особенностей как вырожденные стационарные точки фазовой функции и точки ветвления, так и логарифмическую особенность.

• II.    Типы особых точек и построение перевальных контуров

Следуя идеологии работ [4–8], в [9] были предложены различные типы равномерных асимптотических разложений интеграла (1) для различных областей значений аргументов x и ν. Опираясь на эти идеи, построим и проанализируем равномерные асимптотические разложения интегрального представления (1). Для удобства в формализации дальнейших построений вместо (1) будем рассматривать следующие эквивалентные представления функции D _{v Л} ( x ) :

D \л ( x ) = J exp { Л ( t ² + tx + v In t ) } • t ¹² dt , (2)

• Y ±

где, как и в (1), контур γ^± определен так, что интеграл (2) сходится при любых (конечных) комплекснозначных x и ν: начинается в третьем квадранте комплексной плоскости переменной t и уходит на бесконечность в первом квадранте, огибая сверху (контур γ⁺) или снизу (контур γ^–) точку «0» (рис. 1). Для выделения регулярной ветви логарифмической функции и функции квадратного корня в плоскости переменной t введен разрез от точки «0», не затрагивающий контура γ^±, а именно: вдоль отрицательной полуоси { Im t <  0, Re t = 0 } в случае обхода точки «0» сверху; вдоль положительной полуоси { im t >  0, Re t = 0 } в случае обхода снизу. Пунктиром на рис. 1 обозначена линия, к которой асимптотически на бесконечности приближаются контуры наискорейшего спуска, соответствующие контуру γ^±. Выбор контура γ^± (контур γ⁺, или контур γ^–) определяет особенности интеграла (1), (2), значимые для построения асимптотических разложений.

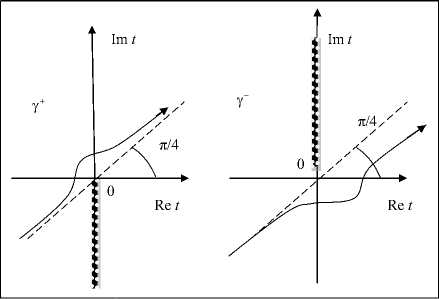
Рис. 1. Контур интегрирования γ для определения функций D _ν ( x )

Выделив явную зависимость от параметра Λ и определив фазовую функцию ин-тегранты (2)

Ф = t ² + tx + v In t ,                                  (3)

мы находим следующие характеристические точки:

• – t_st , морсовские (не особые) стационарные точки A ₁ фазовой функции (здесь и далее для идентификации типов критических точек фазовой функции мы используем обозначения, принятые в теории катастроф, см., например, [10])

tst 12 = 4 (-x ± Vx2 - 8V ), tst 12 * 0, как решения уравнения:

2 • tst2 + x + v   = 0;(5)

tst

• -    t_st * , вырожденные (особые) стационарные точки A 2 фазовой функции

tst *=— 4 , tst ** 0,(6)

возникающие при условии:

x2 = 8v;(7)

• -    t p = 0 , точка полюса (ветвления) порядка 1/2 для предэкспоненциальной функции (амплитудной функции подынтегрального выражения);

• -    t _ln = 0 , точка логарифмической особенности фазовой функции (точку ветвления и логарифмической особенности t _ln = t p = 0 будем обозначать единым символом t p = 0 , а ее особенность - р _{/2 ln} );

• –    t_st ⁰ , особая (логполярная) точка слияния одной стационарной точки A ₁ и точки t p = 0 (с обозначением A 1 / P_{1/2 ln} ) при условии:

ν = 0;                                          (8)

• –    центральная особая точка Σ, соответствующая слиянию всех стационарных точек, точки ветвления и точки логарифмической особенности при условии:

x = v = 0 .                                     (9)

Геометрия особых точек (особенностей) интеграла (1), (2) в пло скости действительных переменных x и ν представлена на рис. 2. В скобках на рис. 2 указаны особенности, имеющиеся у интегранты (2), но не вносящие вклад в асимптотические разложения при заданном контуре интегрирования (рассмотрен контур у⁺ ). Анализ структуры особенностей совместно с анализом допустимых трансформаций контура у ± позволяет предложить различные равномерные асимптотические представления, справедливые в различных областях пространства { x , v } .

Согласно работам [4–7], структура равномерных асимптотических разложений определяется типом особенностей интегранты: вырожденные критические точки дают вклад, представляемый специальными функциями волновых катастроф, особенности типа точки ветвления или полюса внеэкспоненциального множителя порождают в асимптотических представлениях члены, содержащие специальные функции краевых катастроф (катастроф с ограничением) с полюсом, или точкой ветвления соответствующего порядка [5; 7; 8]. Что касается логарифмической особенности, то, как мы покажем ниже, она также важна для корректного построения равномерных асимптотических разложений и приводит к необходимости введения специальных функций, содержащих эталонную логарифмическую особенность – это обобщенный интеграл Френеля, или интеграл Бёмера [11]. Следствием введения разреза для выделения регулярных ветвей функций интегранты (2) в комплексной плоскости переменной t является различие в асимптотиках интегралов (1), (2) для контуров γ⁺ и γ^–.

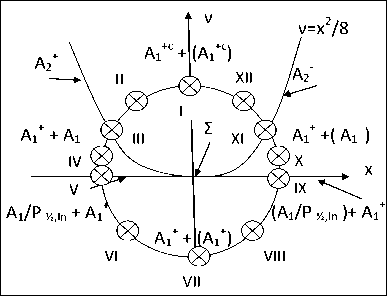
Рис. 2. Геометрия особенностей интеграла (2)

Далее мы ограничимся анализом асимптотик функции D ⁺ _{v Л} ( x ) (контур y⁺). Отличия в рассмотрении функции D \_Л ( x ) (контур Y^-) не существенны и представляют сведение особенностей интегрального представления (2) для γ^– к соответствующим особенностям для функции D ⁺ _{v Л} ( x ) при учете возможных деформаций контура y^- в перевальный контур.

Асимптотические разложения функции D ⁺ _{v Л} ( x ) при Л >>  1 будем рассматривать в соответствии с круговой диаграммой рис. 2, иллюстрирующей связанность различных областей значений переменных x и ν, что позволяет проследить переходы между различными особенностями и преобразование перевальных контуров.

Для расчета членов асимптотических разложений требуется трансформировать исходный контур y⁺ (рис. 1) в перевальный контур у⁺ , удовлетворяющий условиям:

• 1)    у⁺ получается из контура Y + непрерывной трансформацией с учетом введенного разреза в комплексной плоскости переменной t , и так же как и γ⁺, начинается в третьем квадранте и уходит на бесконечность в первом квадранте, огибая сверху точку «0»;

• 2)    у⁺ проходит через все стационарные (перевальные) точки, которые допускаются при описанном выше преобразовании;

• 3)    функция

• - Im ( Ф ( t ) ) = - 2 ар- x p - v • arg ( t ) , где t = a + i p ,             (10)

убывает на линиях контура у⁺ , уходящих от стационарных точек.

Последнее условие реализуется, если элементы контура у⁺ располагаются в областях «невозрастания» функции (10) относительно ее значения в соответствующей стационарной точке. Границы этих областей задаются уравнением:

Im ( Ф ( t ) ) = 2 ав + x в + v- arg ( t ) = Im ( Ф ( t st ) ) .             (11)

В отсутствие разреза комплексной плоскости в качестве элементов перевального контура, обеспечивающих выполнение условия (10), обычно берут контуры наиско- рейшего спуска. Последние задаются уравнением:

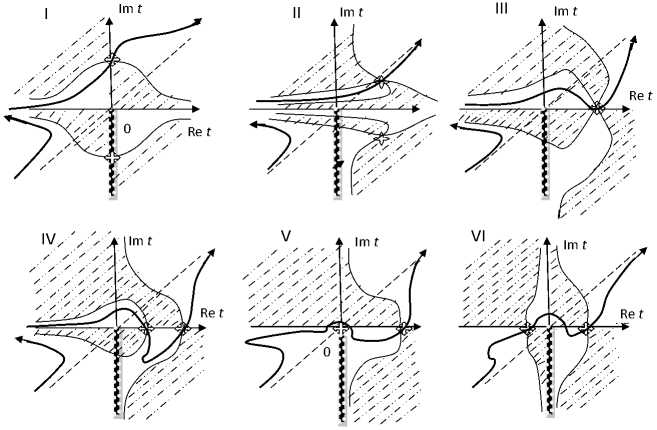
Re(ф(t)) = а2 -p2 + xa + v^In(д/а2 +p2 ) = Re(ф(tst)) (12) с выбором решений, обеспечивающих выполнение условия (10). Наличие разреза не всегда позволяет использовать в качестве элементов у+ контуры наискорейшего спуска, что и позволяет говорить о вкладе особой точки P1/2,ln в асимптотику функции (2). Вид перевальных контуров, построенных для различных областей круговой диаграммы рис. 2, приведен на рис. 3. На данных схемах также указаны: «запрещенные» (где интегранта в (2) экспоненциально растет при Л ^ +да) и «разрешенные» (где инте- гранта в (2) экспоненциально убывает при Л ^ +да) области для контура у+, границы которых определены из (11), расположение стационарных точек (4), (6).

Отметим также, что введение разреза и выделение регулярной ветви логарифмической функции и функции квадратного корня определяет функцию (2) с точностью до множителя:

D\,Л (x) = D±,Л (x) • exP (-2пЛvn) • (—1)n ,(13)

где D ± _Л ( x ) - функция (2), определенная для следующего выбора аргумента комплексной переменной t :

• п

• - 2 < Arg ( t )< у.

Учитывая это, далее мы приводим расчетные формулы асимптотических разложений только для функции D + _Л ( x ) .

• III.    Равномерные и неравномерные асимптотические разложения функции

D : , л ( х )

В соответствии с круговой диаграммой особенностей (рис. 2) и данным выше анализом построения перевальных контуров (рис. 3), нетрудно получить следующие асимптотические формулы для оценки функции D + _Л ( x ) (табл. 1).

В случаях, обозначенных в табл. 1 номерами IV.–V.–VI, используется специальная функция (интеграл Бёмера – Френеля [11]):

B ± ( X ) = j exp { z ( ± t + Х ln( t ) } dt . (15)

В (15) контур у^- для знака «+» прОходит, огибая точку «0» снизу, по верхней части комплексной плоскости переменной t с разрезом от точки «0» вдоль положительной части мнимой оси, что обеспечивает выделение регулярных ветвей логарифмической и корневой функций и не затрагивает контур γ ; для знака «–» в экспоненциальном ядре контур у⁺ и разрез выбираются симметричными у^- относительно оси Re t .

Отметим эффект влияния разреза на комплексной плоскости переменной t на структуру асимптотических разложений, представленных в табл. 1. При переходе от области Vl к областям VII и VIII перевальный контур у⁺ «скачком» перестраивается при переходе через точку x = 0 так, что стационарная точка A - (область VIII) оказывается незначимой. Заметим, что для контура у ^- такой переход также происходит в этой точке x = 0, ν < 0 (область VII). Данный эффект известен как «эффект Стокса» в асимптотических разложениях интегральных представлений [13; 14]. При этом непосредственно на численное значение асимптотического выражения такая перестройка не сказывается, поскольку вклад «потерянной» точки в эффекте Стокса оказывается экспоненциально малым (по Λ). Данное утверждение относится не только к области эффекта Стокса, но и ко всей области значений ν < 0. Можно показать, что при изменении параметра ν от 0 + C _ν до 0 – C _ν ( C _ν > 0) аргумент функции Бёмера – Френеля переходит от положительных значений к отрицательным, а соответствующее значение этойj функции варьируется по параметру Л от величины ~ Л ^ до величины ~ Л^{- 1} / ² • e ^Лп^ (см. табл. 1: Vl, VII, VIII). Поэтому вклад второй морсовской точки A + (правой на рис. 3, области VI, VII, VIII) становится по отношению к главному члену (вкладу левой морсовской точки A + ) экспоненциально малым. При слиянии этой точки с особенностью P _1/2,ln и формировании особенности A ₁/ P _1/2,ln в области IX вклады обеих точек становятся формально соизмеримыми ( ~ Л^{- 1} / ² • e ^Лпх' , v >  0 , ситуация VIII, IX, X на рис. 3). Однако в этом случае проведение контура у⁺ через точку A 1 ^- уже невозможно из-за наличия разреза (эффект Стокса).

Несмотря на экспоненциально малый (по Λ) вклад второй морcовской точки в областях VI, VII, мы сохранили это слагаемое в табл. 1 (дано в скобках), поскольку оно

Im t

VII ^{Im t}                      VIII I m t                    _IX i m t

Re t

Re t                                    Re t                           0 Re t

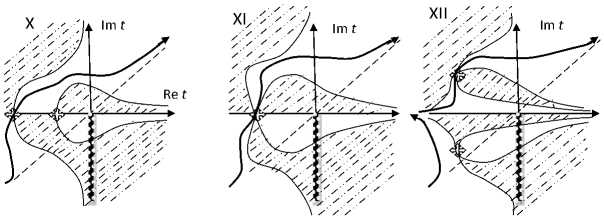
Рис. 3. Вид перевальных контуров у ⁺ для различных точек круговой диаграммы рис. 2

существенно при описании эффекта надбарьерного отражения, имеющего именно экспоненциально малый характер.

Также укажем важное соотношение между функцией (2) при ν = 0 и функцией Т. Пирси [15], использующееся для построения равномерных асимптотических разложений интегральных функций, имеющих вырожденную стационарную точку типа A ± ₃ (см., например, [4-7]):

D ±д (x ) = I (0, x) + i • I (0, - x),                           (16)

где

I ( X 1 , X 2 ) = J exp { i ( t ⁴ + X 2 1 ² + X 1 1 ) } dt , ^γ

Таблица 1

№ области на рис. 2	Тип особенности	Границы области в пространстве действительных переменных x и ν	Вид асимптотики	Расчетные формулы (для коэффициентов до членов порядка O ( л					l —- 1	) )
1	2	3	4	5
XII.– I.–II.	A + C 1	v> C v> 0 2 1 > — = 8>0 8v	D +Л ( x ) ” „i 0 „Г / A - 1/2 « e • e • / 1 •Л	® = л{ Г = -Л	x 2 ^^^ш ^^^^^^^^^^^п 8 f	v + — 2 • V1	"ln v — 1f - 2   JJ ^8-2 + v arg ( ta ) J
				/14-		2	1/4	i Г n		11 ) — arg ( t s, ) ] ,
					^v^	(1—	8) J ^exp 1	2 - 2 arg	(ф
				где
				arg ( t st )	= arg ^—		x + ' л l-'O- — 42	8 ) J = arcctg		( — x )
										12/2v ( 1 — 8 ) J
				arg ( ф	) = arg ( 4 ( 1 — 8 ) — 4 i •			sign ( x Ы80 — 8 ) ) =
				=—sign ( x ) • arctg уц I V1 — 8 J
II.– III.–IV.	A +	( v + Av ) > C v > 0 ; ( x + A x ) 2 ~1 ; 8 ( v + Av ) ( x + A x ) <- Cx < 0 ;	D +л ( x ) « e • { V ( X ) 1 1 -A-1/3 + + V. ( X ) 1 2 -A-2/3 }	н= Л 1 л. ; Л	v^-(v) —	3 — 2 1/3 •	fi x in l 4 J J 1 x| —A x + Av 4	x — •A x + in 4	f x |)     1 U •Av l 4 J J
		2 — = 8 = 1	(здесь V (λ) И V л ' ( Л ) -функция Эйри и её производная, определенные формулами из [12])	, 2 7п		3/4	П
		8v		11 ^ I |1/6         I 11/12 x м / 2 « 0 (расчетные формулы приведены для линейного приближения в Θ и λ, «нулевого» приближения в коэффициентах l 1 и l 2 метода локальной асимптотики [5–7])
IV.	’ + A -	v> C v > 0 x< —Cx <0 x 2 — = 8> 1 8v	D +л ( x ) ” « e ' 0 1 • ' •Л-1 / 2 + + e ' 0 2 • / 2 •Л-1 / 2	01 = Л-	x 2 • 8 +v^	( - 1 l. f l	— 71 — 8—1 ) + x u • 1+71 — 4	8—1 ) ) — 2 _	^
				0 2 = Л	x 2 — 8 +v^	' —1 + 71 — 8-1 ) + "hf x • (1—V1— l4 v		8—' Й—! ' J 2
				' 1 =1	f 1 1	1 — 8—	1/4 )            f .n •exp i J       l 4	J
				' 2=1	П f fl 1	1 — 8—	1/4 1 1 •exp1 — i	n) 4 J

1	2	3	4	5
IV.– V.–VI.	A + A + 1 / P 1/2,ln	v ~0 ; x <- C <0 ; x — = 8 ; 8v δ > 1 при ν > 0	D + , л ( * ) “ == e i ® B - ( Z ) 1 Л + + e i ® ■ 1 2 ■Л- 1/2 (здесь B ~W — функция Бёмера, обобщенный интеграл Френеля [11])	0 1 = a-	2 f-( V1 -8 -1 - 1 )+ x +v- In I      ■( V1-8-1 -1) 1 +1 (4Л v V           /) 2
				®-ЛvIn ( Л x ) . ( 1 + O ( 8-1 ) ) λ = Λν
				02 = a-	x ^- ( -1 - V1-8-1 ) + +v- lnf.+ 71-8-1))-1 ( 4 (             /J 2
				,   1   ,    2П f 1 Vм V) l = —;=, L = h-г- ----- 7   ■ exp 1 —
				1 x	' 2 ^| x | V 1 8 1 J       4 4J
VI–	A + A 1
VII.– VIII–	+	при x > 0 x 2	D v, A ( x ) « ≈ ei Θ 1 ⋅ e Γ ×	0 1 =Л^	- x ■ ( x + V x 2 - 8v ) +
IX.– X.	( A 1 + )	v<— 8	x 1 1 ■ Л- 12 +		+v- lnl —■( x + V x 2 - 8v)l- — V4 (              ) J 2
			[e i® 2 ■ 1 2 -Л " 12'	Г 0-	v
			x < 0 V           7	02 = A-	- x ■ ( x - V x 2 -8v ) +
					+v- InV^- ( x -V x 2 -8v| ) J-"^
					/2Й           .n)
				l 1 1 ( x2	1/4 exp 1 i 1 - 8v )        V 4J J 2п      Г.П)
				l) ( x 2	1/4 exp 1 1 i. 1 - 8v )        V 4J
X.– XI.– XII.	A -	( v + Av ) > C v >0 ; ( x + A x ) 2 ~1 ; 8 ( v + Av ) ( x + A x ) > Cx >  0 ; 2 — = 8 = 1 8v	D +л ( x ) ~ ≈ ei Θ⋅ e Γ× x { w , ( -Z ) l 1 -A- 1'3 + + W 2 ' ( -Z ) l 2 -Л- 2'3 } (здесь W2 ( X ) и wkM - вторая функция Эйри и её производная, определенные формулами из [12])	0 x Л 10 0 ХхЛ2/3 , w l1    ” x 1,6 1 2    x 0 (расчет для лин «нулев в коэфф локаль	। 3 2     , I x )) x ,   , I x VI x +v-In          A x + In    -Av^ V 16         V 4 JJ 4        V 4 J ■ ( v + Av ) " x 1/3                          1 ---A x - 2 ■ x 2,3 - Av 2                  J _ Vn 21/4 v1/12 ные формулы приведены ейного приближения в Θ, Г и λ, ого» приближения ициентах l 1 и l 2 метода ой асимптотики)

а контур γ начинается в секторе комплексной плоскости переменной t , определенном условием π ≤ arg( t ) ≤π , и уходит на бесконечность в секторе комплексной плоско-41

сти, определенном условием: 0 ≤ arg( t ) ≤π .

Соотношение (16) позволяет связать свойства асимптотических представлений функций (2) и (17).

• IV.    Заключение

Представленные асимптотические разложения функции Вебера – Эрмита (1), (2) позволяют исследовать целый класс волновых задач, в которых используется параболическая модель профиля неоднородности, пространственные масштабы которой существенно превышают длину волны, например: оптоволоконный канал, ионосферный слой и др. В частности, удается получить простые формулы для расчета волновых полей, формирующихся в неоднородной среде, с учетом эффектов частичного отражения волн от таких неоднородностей, дифракционного захвата в неоднородный канал, дифракционной деградации волноводных структур.