Спецификация модели параллельных и распределенных вычислений GraphPlus на основе логики TLA

Параллельные и распределенные вычислительные процессы сложны для понимания. В силу ограниченных возможностей человеческого восприятия трудно предвидеть все особенности, возникающие в процессах, одновременно протекающих в разных точках пространства. Имеется множество специфических ошибочных ситуаций (тупики, гонки, отталкивания), которые выявляются только сложным анализом. Поэтому актуальной является задача построения формальных моделей, облегчающих анализ и конструирование параллельных и распределенных процессов и порождающих их алгоритмов и программ.

В области разработки прикладных параллельных алгоритмов развиваются два направления. Первое направление основано на построении модели по информационно-логической структуре конкретного численного алгоритма на этапе его распараллеливания [1]. Второе – на обобщении свойств вычислительных процессов для различных по назначению алгоритмов численного моделирования [2]. В любом случае требуется однозначное понимание особенностей поведения процесса. В статье описывается семантика вычислительной модели GraphPlus, которая используется в рамках второго подхода к синтезу параллельных процессов вычислительных алгоритмов [3].

Неформальное определение вычислительной модели GraphPlus

Модель GraphPlus является примером гра- фической объектной модели, представляющей собой граф, в вершинах которого находятся объекты разных типов, а связи передают статические отношения между объектами.

Структура произвольного параллельного алгоритма, пример которой представлен на рис.1, образована объектами двух типов: “неподвижными” или P-объектами и “подвижными” или M-объектами.

P-объект (“неподвижный” объект) в модели вычислений является функциональным аналогом процесса. Все действия, связанные с P-объектом, выполняются последовательно. Состояние P-объекта, хранимое в его переменных-членах, обычно соответствует некоторой области данных, за обработку которой он отвечает. Состоянием P-объекта может быть, например, сегмент из точек сеточной области в термодинамических расчетах.

M-объект (“подвижный” объект) в модели вычислений является функциональным аналогом сообщения, при помощи которого взаимодействуют процессы (P-объекты). Состояние M-объекта, хранимое в его переменных-членах, например, может соответствовать точкам на границах сегментов сеточной области в термодинамических расчетах.

Вычисления на модели интерпретируются как одновременный обход несколькими M-объектами структуры из P-объектов. Обход выполняется по связям, обозначенным сплошными линиями. Текущее состояние объектов на рис. 1 обозначается при помощи задания взаимного пространственного расположения и способом прорисовки контура. В процессе вы-

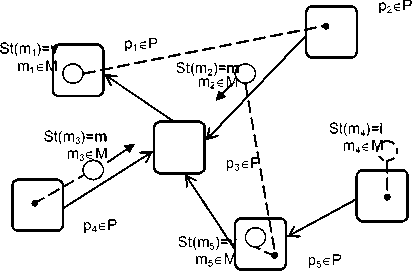
p 6 ∈ P

Рис. 1. Мгновенный снимок структуры параллельного вычислительного процесса в модели GraphPlus числений допустимы следующие состояния объектов модели. M-объект может находиться в неактивном состоянии St[m] ='i' . На рис. 1 это объект m4, обозначенный пунктирным контуром. Активные состояния M-объектов St(m) ='m' ∨ St(m) ='v'на рис. 1 обозначаются сплошным контуром. Находясь в активном состоянии, M-объект может либо перемещаться по связям между P-объектами (состояние перемещения St(m) ='m' показано стрелками), либо посещать P-объект St(m) ='v'(кружок содержится внутри квадрата – состояние посещения).

В процессе описанного выше взаимодействия P-объект может находиться в двух состояниях: состоянии посещения и свободном состоянии. Гарантируется исключительно парное взаимодействие P- и M-объектов. Каждый P-объект в любой момент времени наблюдения посещается не более чем одним M-объектом.

С каждым объектом типа P или M дополнительно связаны переменные, которые хранят состояние объекта, определяемое конкретным численным алгоритмом. Это состояние изменяется только в процессе “посещения”. После посещения некоторого объекта p M-объект может направиться к любому из соседних объектов p ′ : N ( p , p ′ ) = 1 , снова посетить только что посещенный объект p или перейти в неактивное состояние St ( m ) = ' i '. В процессе посещения возможна активация любого неактивного M-объекта, связанного с посещаемым P-объектом x .

Метод описания дискретных систем с использованием темпоральной логики

Для формализации представленного описания вычислительной модели воспользуемся специальной темпоральной логикой TLA (temporal logic of actions), предложенной Лампортом [4,5]. Удобство TLA при формализации модели GraphPlus заключается в использовании переменных для представления состояния вычислений (как в традиционных языках программирования) и возможности однозначного сопоставления модели в терминах TLA со структурным представлением в виде графа рис. 1.

Пусть вычислительный процесс представлен множеством своих историй s s : бесконечных последовательностей дискретных состояний s , причиной изменения которых во времени являются действия A

A ₁ A ₂      A ₃ A ₄

5 0 —— 5 1 —— 5 2 —— 5 з ——... ^.           ( )

Моменты наблюдения состояний связаны с отсчетами дискретного времени. Известно, что, не уменьшая выразительной силы описания важных свойств реальных дискретных систем, можно ограничиться рассмотрением только бесконечных историй, порожденных последовательностью неделимых (атомарных) действий из некоторого конечного множества. Тогда модель системы в темпоральной логике — это формула, смысл которой определен в терминах историй (1). Интерпретация формулы модели F (обозначается символом [[.]] ) состоит в сопоставлении некоторой истории значения истина или ложь:

(5 0 , 5 1 , 52, ^ [[ F ]] - а [[ F ]]:St > { И , Л }.(2)

Множество историй, для которых интерпретация формулы (2) истинна, однозначно определяет дискретную систему в темпоральной логике. Поэтому формула F является математическим описанием дискретной системы, эквивалентным множеству историй (1).

Связь между состоянием, множеством переменных и множеством значений переменных модели передается в виде sn :Var → Val .             (3)

То есть под состоянием понимается функция (3), отображающая множество переменных Var на множество значений Val. Математические выражения, построенные из переменных, знаков математических операций, знаков отношений, логических связок, кванторов и т.п. называются функциями состояния и интерпретируются согласно выражению def

s [[ f ]] == f (V v ': s [[ v ]]/ v ).       ⁽⁴⁾

Выражение (4) означает, что если вместо каждого вхождения переменной в функцию состояния подставить ее значение, то получится интерпретация для состояния s . Специальным случаем функции состояния является предикат состояния. Предикат состояния – функция состояния, принимающая значения истина или ложь.

Действие – это выражение, аналогичное функции состояния по своей структуре, которое дополнительно включает переменные с символом апострофа ('), принимает значения истина или ложь и интерпретируется в виде def

s [[ A ]] t == A ( V ' v ': s [[ v ]]/ v , t [[ v ]]/ v ' )• ⁽⁵⁾

Таким образом, согласно (5) формула для действия дает ответ на вопрос: могут ли два состояния s и t быть соседними в некоторой истории вида (1).

Темпоральные формулы интерпретируются согласно (2) для историй. Поэтому вводится специальный модальный оператор ( □ ) “всегда”, смысл которого определяется через интерпретацию следующим образом:

def

^ [Р F ]] ==V n е N: ( s „ , s n _+b s n ₊₂ , _ )[[ F ]]. ⁽⁶⁾

Структуру формулы F составляют функции состояния и действия, поэтому для применения выражения (6) для интерпретации любых темпоральных формул смысл функций состояния и действий расширяют на бесконечные истории следующим образом:

def

( s 0 , s 1 , s 2 , ^ )^[[ A ^]] == s 0 ^[[ A ^]] s 1 ,

( s 0 , s 1 , s 2 ,_) ^[[ P ^]] = s o^[[ P ^]].

Тогда описывать бесконечные истории можно на основе следующих интерпретаций формул, построенных из действий и состояний с использованием модального оператора □ “всегда”:

(s 0 , s 1 , s 2 ,^) [[ □ A ]] = f

^V n e ^N : ( ^s „ , s n _+b s n + 2 ,_)^[[ A ^]]    . n e ^N : s „ ^[[ A ^]] s „ _{+ 1},

(s 0 , s i , s 2 ,_)[[ □ P ]] ^V n e N: s n [[ P ]].

Семантика логической основы формулы F передается выражениями def

^ [[ - F ]] ==- ^ [[ F ]], def

a [[ F л G ]] == a [[ F ]] л a [[ G ]]

и распространяется на другие логические связки и кванторы очевидным образом по их определению.

Таким образом, используя традиционную математическую нотацию, расширенную знаками (') и ( □ ), можно описать множество историй вычислительного процесса.

Специализация темпоральной логики по Лампорту

Для практически важных дискретных систем, в том числе для вычислительных процессов, требуется рассматривать еще более узкий класс множеств всех историй, а именно историй инвариантных по отношению к преобразованию дублирования одного состояния в соседних отсчетах времени (stuttering). Синтаксически это ограничивает рассмотрение всех темпоральных формул только формулами, сводимыми к виду (7), которые и называются формулами TLA.

def ф== I л^[N]f лF .        (7)

Формула (7) имеет следующую структуру: I – предикат состояния, описывающий начальное состояние (вычислительного) процесса; N – действие, задающее множество всех атомарных операций системы; множество формул вида WF и SF определенных для подмножества атомарных операций из N. До- полнительные синтаксические элементы TLA определяются через введенные выше обозначения посредством соотношений (8)-(18).

def

5 [[ Enabled A ]] ==3 1 e St: 5 [[ A ]] t    (8)

def f ==( v1, v 2, v 3,—) f ' = ( v 1, v 2, v 3,—)' = (v1, v 2, v ‘ ,—)

def unchanged (f) == f = f'

def

[ A ] f == A v ( f = f ' ) = A v unchanged ( f )(H)

def

{A == A л ( f * f ' ) = A л — unchanged ( f )

def

◊ F ==—□— F

⁵⁵ o , ⁵ i , ⁵ 2 ^{, —} [[ ◊ F ]]    I n e N: (^ , s _{n +} i , s _{n +} 2 ^{, —} [[ F ]]

(⁵ 0 , ⁵ 1 , ⁵ 2 , ^— [[ □◊ A ^{]] V n e} N: 3 m ^{e N: s} n + m ^[[ A ^{]] s} n + m ₊ i

(5 0 , 5 1 , 5 2 ,—)[[◊□ A ]] = 3 n e N : V m e N : 5 n ₊ „ [[ A ]] 5 n ₊ „ ₊i

WF_f ( A ) = e = ( □◊ A) f ) v ( ^o— Enabled (A) _f )

SF_f ( A ) = e = ( □◊( A)_f ) v ( ◊□— Enabled (A} _f )

Подробное объяснение определений (8)(18) и их словесная интерпретация приведены в работе [4]. Для понимания модели GraphPlus существенным является смысл выражений (11), (17) и (18). Определение (11) читается “либо выполнено действие A, либо состояние системы, описываемое переменными f, не изменилось”. Определение (17) называется “справедливостью в слабом смысле” (weak fairness). Оно читается следующим образом: “если, начиная с некоторого момента времени выполнить действие A возможно, и эта возможность сохраняется неопределенно долго, то действие A будет выполнено неопределенно много раз”. Определение (18) называется “справедливостью в сильном смысле” (strong fairness). Оно, в отличие от (17), в качестве условия выполнения требу- ет, чтобы, начиная с некоторого момента времени, действие можно было бы выполнить неопределенно много раз. Из смысла (17)-(18) очевидно следует назначение условий F в формуле (7) – при сохранении инвариантности к stuttering–преобразованию исключить из описания истории, в которых N может выполниться, но не выполняется бесконечное число отсчетов дискретного времени.

Спецификация модели GraphPlus

В силу того, что модель GraphPlus вводит специальные семантические понятия объектов, обладающих состоянием, потребуется способ связи объектов с множеством переменных состояния. Для этого введем функции, сопоставляющие объект модели GraphPlus переменной:

o []:Obj ^ Var.          (19)

Будем считать, что все переменные состояния в формулах модели вычислений заданы в виде (19), а вспомогательные переменные (константы TLA) заданы обычным способом.

Определим множества объектов модели GraphPlus следующим образом:

P c Obj M c Obj s e Obj;

P n M = 0 , P n { s } = 0 , M n { s } = 0 ;

P ₊= P u { s }, M ₊= M u { s }.

Здесь ε – описывает специальный “нуль” объект, a P ₊ и M ₊ множества P- и M-объектов, расширенные “нуль” объектом. Обозначим домены значений объектов модели, как D_P c Val и D M c Val. Каждому M-объекту будут соответствовать переменные модели, задаваемые функциями /~[]: M ^ V m m []: M ^ V_M, а каждому P-объекту – функциями ~ []:P ^ V ~ ~[]:P ^ V n p []:P ^ V p . Свойства множества переменных, на которые функционально отображаются множества объектов модели, заданы ниже следующими соотношениями:

V_M ~ ⊂ Var V_M ⊂ Var V_P ⊂ Var V_P ~ ⊂ Var ; V _M ~ ∩ ( V M ∪ V P ∪ V _P ~ ) =∅ , V M ∩ ( V _M~ ∪ V P ∪ V ~_P ) =∅ ; V P ∩ ( V M ∪ V _M~ ∪ V ~_P ) =∅ , V ~_P ∩ ( V M ∪ V _M~ ∪ V P ) =∅ .

Будем описывать отношения инцидентности ( N и L ) между объектами модели, показанные на рис. 1 в префиксной форме в виде специальных предикатов

N (,): N ⊆ P × P и L (,):M → P.

Для описания динамики изменения состояния в модели GraphPlus определим четыре функции:

newP (,) : D_P × D_M → D_P – новое состояние посещаемого P-объекта;

newM (,) : D_P × D_M → D_M– новое состояние посещающего M-объекта;

activate (,,) : M × D_P × D_M → P ₊ – функция активации локальных M-объектов;

next (,) : D_P × D_M → P ₊ — переход M-объекта к следующему P-объекту.

Обозначив множество всех отношений в модели через

ℜ = N ∪ L ∪ newP ∪ newM ∪ activate ∪ next ^, определим модель GraphPlus как

Ψ = (P,M, ℜ , Φ ) ,         (20)

где Ф – формула TLA, описывающая динамику поведения вычислительного процесса. Структура формулы определяется в соответствии с графом модели, пример которого показан на рис. 1 выражениями (21)-(28).

def

φ== I ∧ ^ [ N ] _f ∧ F       (²¹)

def

I == ∧∃ y ∈ M : ( m ^~[ y ] ≠ ε ∧ m ^~[ y ] ∈ P ) ∧∀ x ∈ P : ^~ p [ x ] = n ^~[ x ] = ε ∧ ∀ x ∈ P, y ∈ M : p [ x ] ∈ D_P ∧ m [ y ] ∈ D_M .

(22) f = ^de = ^f (^~ p [ x ]: x ∈ P; m ^~[ y ]: y ∈ M; n ^~[ x ]: x ∈ P; p [ x ]: x ∈ P; m [ y ]: y ∈ M) (23) def

N == ∨∃ x ∈ P, ∃ y ∈ M: A ₁( x , y )

∨∃ x ∈ P, ∃ y ∈ M : A ₂( x , y )

def

F == ∧∀ x ∈ P, ∀ y ∈ M: SF_f ( A ₁( x , y ))

∧∀ x ∈ P, ∀ y ∈ M : WF_f ( A ₂( x , y ))

A ₁( x , y ) = ^de = ^f ∧ p ^~[ x ] = ε ∧ m ^~[ y ] = x

∧ ^~ p ′[ x ] = y

∧ p ′[ x ] = newP ( p [ x ], m [ y ])

∧ m ′[ y ] = newM ( p [ x ], m [ y ])

∧ n ^~′[ x ] = next ( p [ x ], m [ y ])

∧ Local ( x , y )

∧ unchanged ( V _Φ \ ( {^~ p [ x ], p [ x ], n ^~[ x ], m [ y ]} ∪ { m ^~[ k ] : L ( x , k )} ) )

def

Local ( x , y ) == ∀ k ∈ M, L ( x , k ) :

∨∧ m ^~[ k ] = ε

∧ m ^~ ′ [ k ] = activate ( k , p [ x ], m [ y ]) ∨ ∧ m ^~[ k ] ≠ ε

∧ m ^~ ′ [ k ] = m ^~[ k ]

def

A ₂( x , y ) ==∧ ^~ p [ x ] = y ∧ m ^~[ y ] = x

∧ ^~ p ′ [ x ] = ε

∧ m ^~ ′ [ y ] = n ^~[ x ] ∧ N ( m ^~[ y ], m ^~ ′ [ y ])

∧ unchanged (V _Φ \ {^~ p [ x ], m ^~[ y ]})

Для структурирования конъюнктов и дизъюнктов в формулах (22), (24)-(28) использован прием, облегчающий написание длинных формул TLA [5].

Начальное состояние системы (22) предусматривает наличие хотя бы одного M-объекта в состоянии перемещения и правильно проинициализированных переменных численного метода.

Множество допустимых действий связано с графической структурой модели. Действия (26)-(27) соотносят каждый подвижный М-объект, каждому неподвижному P-объекту, определяя, при каких условиях возможно соответствующее посещение и последующая активация новых M-объектов.

Действия (26)-(27) должны быть “справедливы в строгом смысле” для предотвра-

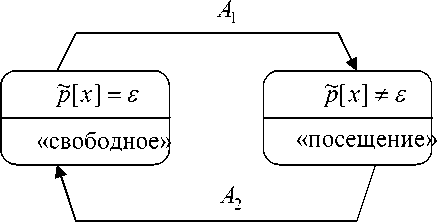
Рис. 3. Схема автомата, описывающего изменения состояния P-объекта

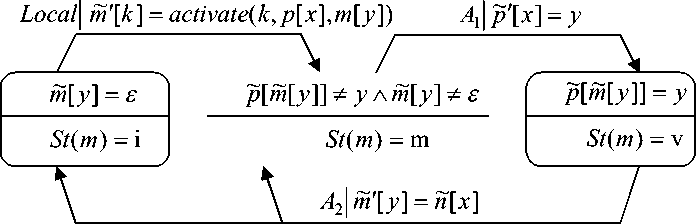
Рис. 2. Схема автомата, описывающего изменения состояния M-объекта

щения ситуации отталкивания одного M-объекта другим при посещении некоторого P-объекта.

Действия (28) задают переход P-объекта в исходное состояние после посещения и управляют переходом M-объекта к следующему P-объекту или в неактивное состояние после посещения P-объекта.

Для действий (28) достаточна “справедливость в слабом смысле”, потому что требуется, чтобы они выполнялись, как только станут готовы к исполнению, а выполнение других действий не может изменить условия их готовности. При реализации модели на многопоточной машине условие (26) обеспечивается путем организации очереди запросов на посещение, в которой операция помещения в очередь реализована в критической секции. Условия справедливости для действий (28) гарантируются диспетчером потоков операционной системы [6].

Соответствие между определением состояний в неформальном описании модели со строгим определением (20) поясняется на рис. 2 и рис. 3.

Заключение

Таким образом, в работе построено математически точное определение прикладной вычислительной модели — спецификация модели GraphPlus. Она описывает вычислительные процессы, возникающие при параллельной и распределенной реализации алгоритмов численного моделирования. Модель позволяет изучать свойства конкретных процессов средствами TLA, в частности возможность параллельного и эффективного распределенного исполнения. Предложенная модель определяет способ реализации вычислительного процесса в распределенной и многопоточной вычислительной среде, как описано в работе [6], что обуславливает ее применимость для конструирования комплексов прикладных программ численного моделирования.