Spectral Subtractive-Type Algorithms for Enhancement of Noisy Speech: An Integrative Review
Автор: Navneet Upadhyay, Abhijit Karmakar
Журнал: International Journal of Image, Graphics and Signal Processing(IJIGSP) @ijigsp
Статья в выпуске: 11 vol.5, 2013 года.
Бесплатный доступ
The spectral subtraction method is a classical approach for enhancement of speech degraded by additive background noise. The basic principle of this method is to estimate the short-time spectral magnitude of speech by subtracting estimated noise spectrum from the noisy speech spectrum. This is also achieved by multiplying the noisy speech spectrum with a gain function and later combining it with the phase of the noisy speech. Besides reducing the background noise, this method introduces an annoying perceptible tonal characteristic in the enhanced speech and affects the human listening, known as remnant musical noise. Several variations and implementations of this method have been adopted in past decades to address the limitations of spectral subtraction method. These variations constitute a family of subtractive-type algorithms and operate in frequency domain. The objective of this paper is to provide an extensive overview of spectral subtractive-type algorithms for enhancement of noisy speech. After the review, this paper is concluded by mentioning a future direction of speech enhancement research from spectral subtraction perspective.
Speech enhancement, additive background noise, noise estimation, spectral subtractive-type algorithms, remnant musical noise
Короткий адрес: https://sciup.org/15013095
IDR: 15013095
Текст научной статьи Spectral Subtractive-Type Algorithms for Enhancement of Noisy Speech: An Integrative Review
Speech is one of the most prominent and primary modes of interaction between human-to-human and human-to-machine communication in various fields for instance automatic speech recognition and speaker identification [1]. The present day speech communication systems are severely degraded due to various types of unwanted random sound which make the listening task difficult for a direct listener and cause inaccurate transfer of information [2]. Therefore, enhancement speech is one of the main motives of various researching endeavors in the field of speech processing over the past few decades. The main objective of speech enhancement is to minimize the degree of distortion of the desired speech signal and to improve one or more perceptual aspects of speech, such as the quality and/or intelligibility.
The quality of speech is a subjective measure which reflects the way that the signal is perceived by listeners. Intelligibility, on the other hand is an objective measure of the amount of information that can be extracted by listeners from the speech signal. These two measures are uncorrelated and independent of each other. A speech signal may be of high quality and low intelligibility and vice-versa [1-4].
The classification of speech enhancement method depends on the number of microphones that are used for collecting speech data, into single, dual or multi-channel. Although the multi-channel speech enhancement is better than that of single channel speech enhancement [1-2], yet the single channel speech enhancement is still a significant field of researching because of its simple implementation and ease of computation. Single channel speech enhancement uses only one microphone to collect noisy speech data [1-4].
The estimation of the spectral amplitude from the noisy data is easier than estimate of both the amplitude and phase. In [5-6], revealed that the short-time spectral amplitude (STSA) is more important than the phase information for the quality and intelligibility of speech. Therefore, single channel speech enhancement is usually divided into two classes based on the STSA estimation. The first class applies subtractive-type algorithms and attempt to estimate the short-time spectral magnitude (STSM) of speech by subtracting the estimated noise spectrum. Here, noise is estimated during speech pauses [7-11, 13]. The other class applies a spectral subtraction filter (SSF) to the noisy speech, so that the spectral amplitude of enhanced speech can be obtained. The design principle is to select appropriate parameters of the filter to minimize the difference between the enhanced speech and the clean speech signal [8].
In real-world listening environments, the speech is mostly degraded by additive noises [5, 9-14]. Additive noise is typically background noise which is uncorrelated with the clean speech signal in nature like white Gaussian noise (WGN), colored noise, multitalker (babble) noise. The background noise may be stationary or non-stationary in nature. Therefore, the noisy signal can be modeled as a sum of the clean speech and the noise signal [9-11, 13] as
y(n) = s(n) + d(n), n = 0,1,2,. ., (N - 1) (1)
where n is the discrete-time index, and N is the number of samples in the signal. Also, y(n), s(n), and d(n), are the nth sample of the discrete-time signal of noisy speech, clean speech and random noise, reactively. Although speech is non-stationary in nature whose spectral properties vary with time, usually the short-time Fourier transform (STFT) is used to divide the speech signal in small frames for further processing [9-15]. Now representing the STFT of the time windowed signals by Yw (o) , Dw (o) , and 5w (o) (1) can be written as [9 -15],
Y w (o) = 5 w (o) + D w (o) (2) where o is the discrete-frequency index of the frame and w is the window (Hamming or Henning window). Throughout this paper, it is assumed that the signal is segmented into frames first and then windowed, hence for simplicity, we drop the use of subscript w from windowed signals. For implementation of speech enhancement method, few assumptions are necessary. First, the speech signal should be stationary; and other, the noise is assumed to be zero mean and uncorrelated with clean speech signal.
The goal of this paper is to provide an integrative review of subtractive-type noisy speech enhancement algorithms. In addition to basic spectral subtraction algorithm [7, 9, 10] other most notable algorithms are spectral over-subtraction (SOS) [15], parametric spectral subtraction (PSS) [16], spectral subtraction based on cross correlation [17], non-linear spectral subtraction (NSS) [18], multi-band spectral subtraction (MBSS) [19], Wiener filtering (WF) [20], iterative spectral subtraction (ISS) [21], extended spectral subtraction (ESS) [22], and spectral subtraction based on perceptual properties (SSPP) [23].
This paper is organized as follows; we start with historical account on the use of enhancement methods of noisy speech. In section II, the principle of spectral subtraction method has been presented. Section III presents various modified forms of subtractive-type algorithms. Finally, the conclusion of review has been provided in section IV.
-
II. Principle of Spectral Subtraction Method
The spectral subtraction is one of the most well-known and computationally efficient methods for effectively, suppressing the background noise from the noisy speech as it involves a single forward and inverse transform. The first comprehensive spectral subtraction method, proposed by Boll [7, 9, 10] is based on nonparametric approach, which simply needs an estimate of noise spectrum and used for both speech enhancement and speech recognition. The spectral subtraction method mainly, involves two phases. In the first phase the average estimate of the noise spectrum is subtracted from the instantaneous spectrum of the noisy speech. This is termed as basic spectral subtraction (BSS) step. In the second phase, several modifications like halfwave rectification (HWR), remnant noise reduction and signal attenuation are done to reduce the signal level in the non-speech regions. It is assumed that the phase of noise has no effect on phase of clean speech because change of phase in the process is not perceived by human ear [5, 6]. Therefore, STSM of noisy speech is equal to the sum of STSM of clean speech and STSM of random noise without the phase information and (2) can be expressed [11] as
|Y(c)| = |5(c)| + |D(c)| (3)
|Y(c)|2 = |5(c)|2 + |D(c)|2 +
5(o)D * (o) + 5 * (o)D(o) (4)
Here, D * (o) and 5 * (o) are the complex conjugates of D(o) and 5(c), respectively. The |Y(o)|2 , |5(o)|2 , and |D(o)|2 , are referred to as the short-time spectrum of noisy speech, clean speech and random noise, respectively. The value of |D(o)|2, 5(co)D * (co) and 5 * (o)D (o) cannot be obtained directly and are approximated as, E[|D(co)|2} , E [5(co)D * (co)} and E {5 * (co)D(co)} ,where E {.} denotes the ensemble averaging operator. As the additive noise assumed to be zero mean and uncorrelated with the clean speech signal, the terms E £5(o)D * (o)} and E {5 * (o)D (o)} reduce to zero [11, 13]. Therefore, (4) can be rewritten as
|Y(c)|2 = |5(c)|2 + |D(c)|2
It is desired to choose an estimate |5(o) | that will minimize the error
E„(0)= ||5(c)|2 - |5(c)|21,
E„(c) = ||5(c)|2 - |Y(c)|2 + E{|D(c)|2}|,
The (7) can be minimized by choosing
|5(c)|2 = |Y(c)|2 - |D(c)|2
where |5(o)|2 is the short-time spectrum of estimated speech and |D (o)|2 is the average noise power which normally, estimated and updated during speech pauses.
In spectral subtraction method, it is assumed that the speech signal is degraded by additive white Gaussian noise (AWGN) and the spectrum of white noise is flat. Hence, the noise affects the speech signal uniformly over the whole spectrum. In this method, the subtraction process needs to be done carefully to avoid any speech distortion. The spectra obtained after subtraction process may contain some negative values due to inaccurate estimation of the noise spectrum. Since, the power spectrum of estimated speech can become negative due to over-estimation of noise, but to get rid of this possibility, therefore, a HWR (by setting the negative portions to zero) or full-wave rectification (absolute value) are introduced. But the HWR introduces annoying noise in the enhanced speech. Whereas, fullwave rectification (FWR) avoids the creation of annoying noise, but it is less effective in suppressing noise. Therefore, HWR is often used in spectral subtraction method due to its superior noise suppression ability. Thus, the complete power spectral subtraction algorithm is given by r{|г(ш)|2 - |5(ш)|2},
Щш)| 2 = j if |У(ш)|2 > ID (ш)|2 (9)
0 else
The enhanced speech is reconstructed by taking the inverse STFT (ISTFT) of the enhanced spectrum using the phase of the noisy speech and overlaps-add (OLA) method [11-14], can be expressed as
5(n) = ISTFT{|5(w)|.exp(/ On the contrary, a generalize form of spectral subtraction (8) can be obtained by altering the power exponent from 2 to b, which determines the sharpness of the transition. |5(ш)|ь = |Г(ш)|ь- |D(ш)|ь,b >0 (11) where b = 2 represents the power spectral subtraction and b = 1 represents the magnitude spectral subtraction. Figure 1, shows the block diagram of spectral subtraction method.
A. Noise Estimation The noise estimation is the most critical part of frequency domain enhancement algorithms because the quality of the enhanced speech depends on the accurate noise spectrum estimation [11]. The noisy signal consists of some portions that have speech activities and some portions that have nonspeech activity called speech pauses. The speech activities means that the portions of noisy speech consists of speech, which is degraded by background noise, whereas the speech pauses are the parts of the noisy speech only with background noise. Moreover, the speech regions are periodic in nature and energy of speech regions is larger than that of non-speech regions while non-speech sounds are more noise-like and have more energy than silence. Silence has the least amount of energy and is the representation of the background noise of the environment. As a result, the SNR’s of speech activity regions are generally higher than that of non-speech regions. Therefore, the enhancement of speech regions is more effective than that in speech pauses [11]. Figure 1. Block diagram of spectral subtraction method. In spectral subtraction method, voice activity detection (VAD) algorithm plays a central role for detecting presence and absence of speech in a noisy speech signal. It gives the values of zeros and one as an indicator of speech pauses and speech activity in each frame. If the noise is stationary, the first 100-200 ms of noisy signal is assumed to be pure noise. To do this, a good estimation can be resulted by computing the average of the noise in silence frame spectra [11]. In presence of non-stationary noise, the noise spectrum needs to be estimated and updated, continuously. The noise estimation can be updated by using the first order relation as |D(ш,к)|2 = A|D(ш,к- 1)|2 + (1 -№,к)|2 (12) where λ (0 ≤ λ ≤ 1) is a time and frequency dependent smoothing parameter whose value depends on the noise changing rate and к refers to the current frame-index. |К(ш, к)|2 represent the short-time power spectrum of noisy speech, |D(ш, к)|2 is the updated noise spectral estimate, and |D (ш, к — 1)|2 is the past noise spectral estimate [18]. In [24, 25] suggested algorithms are based on finding the minimum statistics of noisy speech for each sub band over a time window.
B. Limitation of Spectral Subtraction Algorithm The major weakness of spectral subtraction method is that after the processing, the enhanced speech is accompanied by excessive remnant noise with musical nature. As a result, the detection of speech pauses is difficult. This noise is generated due to the in-accurate estimation of noise from each frame i.e. mismatch between the noise spectrum estimate and the instantaneous noise spectrum [11]. This noise sometimes more disturbing not only for human ear, but also for speaker recognition systems. Several publications have been existed in the literature for the modifications of the spectral subtraction method to combat the problem of remnant noise and musical noise artifacts. III. Spectral Subtractive-Type Algorithms
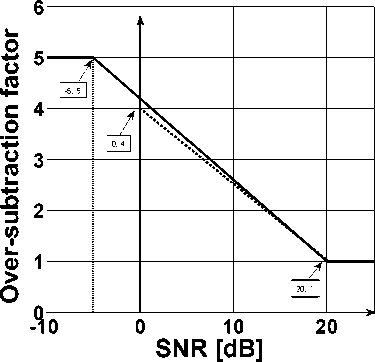
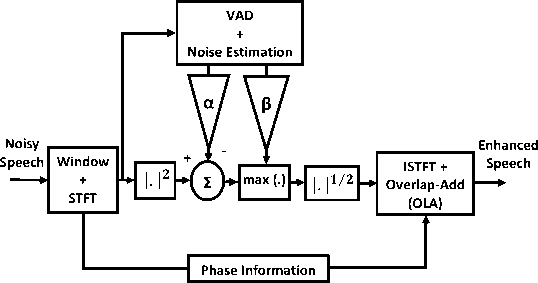
A. Spectral Over-Subtraction Algorithm An improved version of spectral subtraction method was proposed in [15] to minimize the annoying musical noise. In this algorithm, the spectral subtraction method [9] is used by using two additional parameters, oversubtraction factor α, and spectral floor parameter β [15]. The algorithm [15] can be described as №)|2 -a.\D(о)|2, |5(w)|2 = ] if ID<«)i2< 1 |У(й) )|2 « +/ else The function of over-subtraction factor is to control the amount of noise power spectrum subtracted from the noisy speech power spectrum and the introduction of spectral floor parameter prevents the spectral components of the resultant spectrum to fall below a preset minimum level rather than setting to zero. To reduce the speech distortion caused by large value of α, its value is adapted from frame to frame. The basic idea is take into account that the subtraction process must depends on segmental SNR. Therefore, the oversubtraction factor can be calculated as «= «0+(SNR -SNR ) ( «min_~« maxmin SNRmin < SNR < SNRmax where ^*=0 ^(^)| SNR (dB) = 10 log10 (2?-1|5(ш)|2 ) Here, the value of «min = 1, «max = «0 , SNRmin = 0 dB, SNRmax = 20 dB and «0 («0 ~ 4), used in (14), is the desired value of « at 0 dB SNR. These values are estimated by experimental trade-off results. The relation between over-subtraction factor and segmental SNR is shown in Figure 2. This implementation assumes that the noise affects the speech spectrum uniformly and the performance of this scheme is restricted in the usage of fixed value of subtraction parameters, which are difficult for real-world noises. Thus, it is not easy to reduce noise without decreasing speech intelligibility and distortion, especially at very low SNRs. In Figure 3, the block diagram of spectral over-subtraction algorithm is shown. Figure 2. The relation between over-subtraction factor and segmental SNR. Figure 3. Block diagram of spectral over-subtraction algorithm. B. Parametric Spectral Subtraction Algorithm In [15], the subtractive parameters have been computed experimentally and have not been selected optimally in any sense. An algorithm is proposed in [16], where the subtractive parameters are selected in mean squared error (MSE) sense to reduce the remnant noise problem linked with spectral subtraction algorithm. The values of subtractive parameters are derived by the parametric formulation of generalized spectral subtraction algorithm (11). The generalized form of spectral subtraction algorithm can also be given as |5(o)|b = a( where a( 2(- = (. ' — ID(Ш)Ib 1} /Ь (17) cu j I о (CO) У Here e(ic) is the a-priori SNR and Sj is constant for a given power exponent b. The values of 5b are 0.2146, 0.5 and 0.7055 for b = 1, 2 and 3, respectively [11]. The value of e(ic) cannot be computed exactly as we do not have access to the clean speech signal. In [8], proposed the approach and in [16], approximated as .Л — (А „Л (|S(—)\2current I „ |S(—)|2previous /1 о\ = (1 - * («к-)|2.u„n. ) + ';'1- ')|2p„„us (18) Here \S(—)|2current = max(\Y(—)|2 - |5(—)|2,0) and ] is a smoothing constant also \S(—)\2previous is the enhanced spectrum computed in previous frame. The first term of (18) is the value of current SNR and the second term is previous SNR. Also, the spectral floor with lower bound ц. Y is used to limit the signal attenuation. The final constrained parametric estimator is implemented as S(—) = (|S(—)|, if \S(—)\ > ц.\Y(—)\ ( ц. Y, else where µ is the spectral flooring constant 0 < µ < 1, and S(—) is the previous estimated amplitude. C. Spectral Subtraction based on Cross Correlation The spectral subtraction based on cross correlation was proposed in [17]. In this algorithm, it is assumed that the noise signal is correlated with clean speech signal. Therefore, in (4) the cross terms cannot be ignore, these terms are used to represent the cross correlations between clean speech and correlated noise. Also, we do not have access to clean speech signal so it is very difficult to estimate cross correlations between clean speech signal and correlated noise. But, since we have access to the noisy speech signal, we can get an estimate of the cross correlation by computing the cross correlation between noisy speech and noise signal.
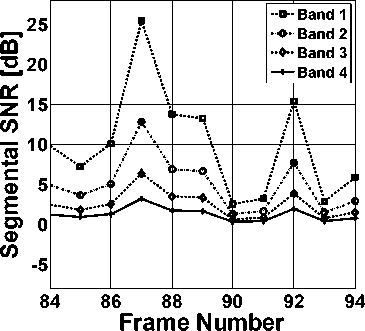
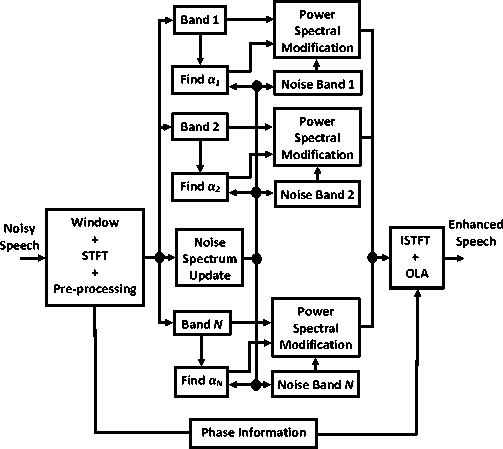
D. Non-linear Spectral Subtraction The non-linear spectral subtraction (NSS) algorithm, proposed in [18], is motivated by the fact that algorithms with fixed subtraction parameters are unable to adapt well to the varying noise levels and characteristics. This approach is a basically a modification on the algorithm proposed in [15] by making the over-subtraction factor frequency dependent and the subtraction process non-linear. Larger values are subtracted at lower SNR and at higher SNR the subtraction applied is minimal. The NSS algorithm can be written as follows: |S(-)| = Г|Y(—)| - ф(—), ] if )У{-)|>#(-) + p.|D(-)| (p. |Y(—)|, otherwise where p is the spectral floor parameter [15], |Y(—)| and \D (—)| the smoothed estimates of noisy speech and noise, respectively. The ф(-) is a non-linear function, calculated for each frame and is dependent on the following parameters: Ф(-) = f{a(—), p(—),|D (-)|j Here, the over-subtraction factor a(—) is computed for each frame к as the maximum noise spectrum (estimated during speech pauses) over the last 40 frames: a(—) = max(| Dk G^X-^^ p(—) is the a-posteriori SNR, and is estimated according to the following relation p(-) = il-lf |D(-)| where |Y(—)|p is the noisy speech spectrum smoothed, with a time-frequency dependent smoothing parameter of value 0.5. E. Multi-band Spectral Subtraction Algorithm In real-world environment, the noise spectrum is nonuniform over the entire spectrum. Some of the frequencies are affected more adversely than others, depending on the spectral characteristics of the noise, which eventually mean that this kind of noise is non-stationary or colored. To take into account the fact that colored noise affects the speech spectrum differently at different frequencies, a multi-band uniformly spaced frequency approach to spectral over-subtraction [15] is presented in [19]. The result of an implementation of four uniformly spaced frequency bands [19] with estimated segmental SNR of bands {60 Hz ~ 1 kHz (Band 1), 1 kHz ~ 2 kHz (Band 2), 2 kHz ~ 3 kHz (Band 3), 3 kHz ~ 4 kHz (Band 4)} of noisy speech spectrum is shown in Figure 4. It can be seen from the figure that the segmental SNR of the low frequency bands (Band 1) is significantly higher than the segmental SNR of the high frequency bands (Band 4) [11, 19]. This phenomenon suggests that the noise signal does not affect the speech signal uniformly over the whole spectrum; therefore, subtracting a constant factor of noise spectrum over the whole frequency spectrum may remove speech also. The multi-band spectral subtraction algorithm [19] is the case of NSS [16]. In this algorithm, the noisy speech spectrum is divided into four uniformly spaced nonoverlapping frequency bands, and spectral oversubtraction is performed in each band, separately. This algorithm re-adjusts the over-subtraction factor in each band. Therefore, the estimate of the clean speech spectrum in the ith Band is obtained by |Si (—)\2 = | |Yi(-)|2 - a.5i. iDi(-)|2, if IS(—)\2 > p.|Y(-)|2 p.\Yi (—)|2, else where — < — < —i+1 where — and —i+1 are the start and end frequency bins of the ith frequency band, ai is the band specific over- subtraction factor which is the function of the segmental SNR of corresponding band. The segmental SNR of ith Band can be computed as (У u,+1 IV.(u)I2\ У + ■) (25) The band specific over-subtraction factor can be calculated, using Figure 2, as «max, if SNR, < SNRmin «max + (SNR, - SNRmin ) (^ ^ ) , SNR max SNR min if SNRmin < SNR, < SNRmax «min, if SNR, > SNRmax Figure 4. The segmental SNR of four uniformly spaced frequency bands of degraded speech. Here «min — 1, «max — 5, SNRmin — 5 dB, SNRmax — 20 dB. The 5, is an additional band subtraction factor that provide an additional degree of control within each band. The values of 5, used in [19] is empirically calculated as most of the speech energy is concentrated below 1 kHz. The negative values of the estimated spectrum are floored. As the real-world noise is highly random in nature. So, improvement in the MBSS algorithm for reduction of WGN is required. However, the performance of MBSS method is better than other subtractive-type algorithm. This algorithm has been applied in different configuration in [26-31]. In [29], perceptually motivated un-decimated wavelet packet filterbank is used to obtain bands. In Figure 5, the block diagram of multi-band spectral subtraction algorithm is shown.
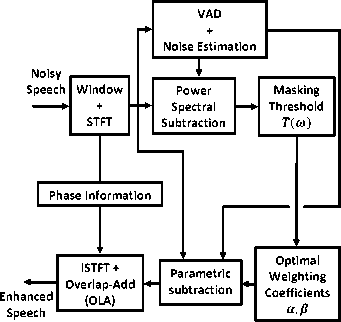
F. Wiener Filtering The spectral subtraction method [9] can also be viewed as a filtering operation [5, 8]. The noisy speech is filtered with a time-variant linear filter where high SNR regions of the measured spectrum are attenuated less than low SNR regions. Therefore, (11) can be expressed as the product of noisy speech spectrum and a spectral subtraction filter (SSF) as |S(u)|‘ — |r(u)|‘ - ID(u)|* — Я(ш). |Г(ш)|» (27) where е [1 - ^] (28) The H(u) is a real function, called the gain of SSF. The gain of SSF has zero phase and its magnitude Figure 5. Block diagram of multi-band spectral subtraction algorithm [31]. response lies in the range of 0 < H(o) < 1. This filter acts as a SNR dependent attenuator. The Wiener filter (WF) is derived from the SSF and is based on the minimum mean squared error (MMSE) between clean speech and the estimated speech. Here, it is assumed that the speech and the noise obey normal distribution and do not correlate. The implementation of a WF requires the power spectrum of the signal and the noise. However, SSF can be used as a substitute for the WF when the signal spectrum is not available. The gain of the WF [4, 20], Hwiener (cu), can be expressed in terms of the power spectrum of clean speech Ps (u) and the power spectrum of noise Pd (u) . But power spectrum of clean speech is not known, the power spectrum of the noisy speech signal Py (u) is used instead as , Ps(u ) _ P (u ) wiener (u)— Py (u) — Ps (u )+ Pd (u ) — _Py_(<u)-Pd_(u2 Py (u ) The weakness of the WF is that it has fixed frequency response at all frequencies and the requirement to estimate the power spectral density of the clean signal and noise prior to filtering. Therefore, non-causal WF cannot be applied directly to estimate the clean speech since speech cannot be assumed to be stationary. Therefore, an adaptive WF implementation can be used to approximate (29) as и Л |^())|2-|^())|2( On comparing Н()) and HA.wiener ()) from (28) and (30), it can be observed that the WF is based on the ensemble average spectra of the signal and noise, whereas the SSF (b = 2) uses the instantaneous spectra for noise signal and the time-averaged spectra of the noise. In WF theory the averaging operations are taken across the ensemble of different realization of the signal and noise processes. Whereas, in spectral subtraction we have access only to single realization of the process. G. Iterative Spectral Subtraction Algorithm An iterative spectral subtraction algorithm [21, 32-34] is motivated from WF [4, 20]. In this technique, the output of the spectral subtraction method is used as the input signal of the next iteration process. As after the spectral subtraction process, the type of the additive noise is changed to the remnant noise. This remnant noise is re-estimated and this new estimated noise furthermore, is been used to process the next spectral subtraction. Therefore, an enhanced output speech signal can be obtained, and the iteration process goes on. If we regard the process of noise estimate and the spectral subtraction as a filter, the filtered output is used not only for designing the filter but also as the input of the next iteration process. The iteration time is the most important factor of this method which effects on the performance of speech enhancement. The larger iteration number will correspond to the better speech enhancement performance with the less remnant noise [31, 33]. H. Extended Spectral Subtraction Algorithm The extended spectral subtraction [22] is based on a combination of adaptive WF and spectral subtraction, and removes the necessity of VAD to estimates the average noise spectrum during speech pauses frames. The key feature of this technique is that it can estimate average noise spectrum continuously even during speech activity without finding speech pause. WF is used to estimate the average noise spectrum and the enhanced speech spectrum is obtained by subtracting the preceding average noise spectrum from the noisy speech spectrum. This algorithm is comparatively much simpler as compared to the other subtractive-type algorithms. I. Spectral Subtraction based on Perceptual Properties The main weakness of spectral over-subtraction algorithm is that it uses the fixed values of subtraction parameters [15]. However, the optimization of the parameters is not an easy task, because the spectrum of most of the additive noise is not flat. An example of adaptation is multi-band spectral subtraction and parametric spectral subtraction algorithms, these schemes adapt the subtractive parameters a and P in time and frequency based on the segmental SNR or in a MSE sense, leading to improved results but remnant noise is not suppressed completely, at low SNR's [16, 19]. For this reason, the selection of proper value of parameters a and P is the major task in subtractive-type algorithms. The concept of masking threshold of human auditory system is explored in [23], to reduce the annoying remnant noise below the noise masking threshold of lean speech signal and to make less speech distortion. In this approach, the subtraction parameters are adapted based on the noise masking threshold of human auditory system to achieve a good trade-off between the remnant noise, speech distortion and background noise. If the masking threshold is high, the remnant noise will be masked naturally and it will not be audible. In this case, the subtraction parameters have their minimum values, thereby reducing speech distortion. However, if the masking threshold is low, the remnant noise is not masked. In this case, it is necessary to increase the values of subtractive parameters. The adaptation of subtractive parameters is done according to the relations as amax, if Т(ш) = Т() amin, if ТО = ТОтах amax / ТОтах - Т(Ш)А + / Т(Ш) - ТОтт \ТОтах -ТОтт/ т‘П \ТОтах - ТОтт , if ТО^Отт, ТОтах] Ртах, if Т()) = ТОтт P = Pmin, if Т()) = Т())тах / Т())тах - Т()) А + „ / Т()) - T())min ' : \Т())тах — Т(Ш)тп) Pmin ^Т())тах — T(Ш)min , if Т(Ш)6 [Т())min , Т())тах ] where атах , amin , Ртах , Pmin and Т())тах , Т())т1п are the maximal and minimal values of a, P and updated masking threshold Т()) , respectively. It can be seen from (32) and (33) that a, P achieves the maximal and the minimal values when Т ()) equals its minimal and maximal values. The noise masking threshold can be calculated from the enhanced speech as the method proposed by [35]. The perceptual properties of human auditory system have been applied in different configuration in spectral domain and wavelet domain [36-37]. In Figure 6 the block diagram of spectral subtraction algorithm based on perceptual properties is shown. Figure 6. Block diagram of spectral subtraction algorithm based on perceptual properties. IV. Conclusion In this paper, an attempt has been made to present the comprehensive overview of research on speech enhancement using spectral subtractive-type algorithms and to provide a year-wise progress to this date. Although significant progress has been achieved in the last few decades, there are many problems yet to be resolved for enhancement of noisy speech. Three factors that deeply affect the performance of subtractive-type algorithms are: i) exact noise estimation, ii) processing of negative spectral components, and iii) the power exponent factor. Among them the basic problem of subtractive-type algorithms are the average noise estimation. Subtraction of large amount of estimated noise makes the enhanced speech distorted, whereas subtraction of fewer amounts of estimated noise then much of the interfering noise remains present in the signal. Although the modified forms of spectral subtraction method suppress the remnant musical noise to some extent, its complete removal has not yet been achieved. Moreover, the spectral subtractive-type algorithms are capable of enhancing the quality of speech signal but fail to enhance the intelligibility of the signal. Although, the researchers primarily focused on reducing the background noise from the degraded speech till now, yet there is a tremendous scope in enhancing the speech intelligibility and boosting up of the speech components.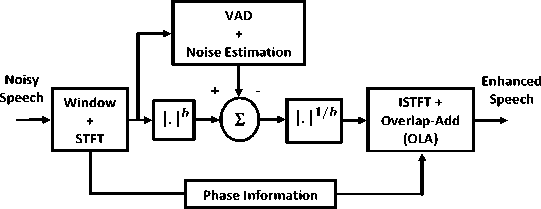
Список литературы Spectral Subtractive-Type Algorithms for Enhancement of Noisy Speech: An Integrative Review
- Y. Ephraim, H. L. Ari, and W. Roberts, "A brief survey of speech enhancement," in the Electrical Engineering Handbook, 3rd ed. Boca Raton, FL: CRC, 2006.
- Y. Ephraim, and I. Cohen, "Recent advancements in speech enhancement," in the Electrical Engineering Handbook, CRC press, ch. 5, pp. 12 – 26, 2006.
- Y. Ephraim, "Statistical-model-based speech enhancement systems," in Proceedings of the IEEE, vol. 80, no. 10, pp. 1526 – 1555, Oct. 1992.
- Yifan Gong, "Speech recognition in noisy environments: A survey," Speech Communication, vol. 16, no. 3, pp. 261 – 291, April 1995.
- J. S. Lim, and A. V. Oppenheim, "Enhancement and bandwidth compression of noisy speech," in Proceedings of the IEEE, Dec. 1979, vol. 67, no. 12, pp. 1586 – 1604.
- L. W. David, and J. S. Lim, "The unimportance of phase in speech enhancement," IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 30, no. 4, pp. 679 – 681, Aug. 1982.
- S. F. Boll, "Suppression of noise in speech using the saber method," in Proceedings of International Conference on Acoustics, Speech, and Signal Processing, April 1978, vol. 3, pp. 606 – 609.
- Y. Ephraim, and D. Malah, "Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator," IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 32, no. 6, pp. 1109 – 1121, Dec. 1984.
- S. F. Boll, "Suppression of acoustic noise in speech using spectral subtraction," IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 27, no. 2, pp. 113 – 120, 1979.
- S. F. Boll, "A spectral subtraction algorithm for suppression of acoustic noise in speech," in Proceedings of International Conference on Acoustics, Speech, and Signal Processing, April 1979, vol. 4, pp. 200 – 203.
- P. C. Loizou, Speech Enhancement: Theory and Practice, Boca Raton, FL: CRC, 2007.
- Kuldip Paliwal, Kamil Wo´jcicki, and Belinda Schwerin, "Single channel speech enhancement using spectral subtraction in the short-time modulation domain," Speech Communication, vol. 52, no. 5, pp. 450 – 475, May 2010.
- S. V. Vaseghi, Advanced Digital Signal Processing and Noise Reduction, IInd ed. NY, USA:Wiley, 2000.
- Leigh D. Alsteris, and Kuldip K. Paliwal, "Short-time phase spectrum in speech processing: A review and some experimental results," Digital Signal Processing, vol. 17, no. 3, pp. 578 – 616, May 2007.
- M. Berouti, R. Schwartz, and J. Makhoul, "Enhancement of speech corrupted by acoustic noise," in Proceedings of International Conference on Acoustics, Speech, and Signal Processing, Washington DC, April 1979, vol. 4, pp. 208 – 211.
- B. L. Sim, Y. C. Tong, J. S. Chang, and C. T. Tan, "A parametric formulation of the generalized spectral subtraction method," IEEE Transactions on Speech, and Audio Processing, vol. 6, no.4, pp. 328 – 337, July 1998.
- Yi. Hu, M. Bhatnagar, and P. C. Loizou, "A cross-correlation technique for enhancing speech corrupted with correlated noise," in Proceedings of International Conference on Acoustics, Speech, and Signal Processing, May 2001, vol. 1, pp. 673 – 676.
- P. Lockwood, and J. Boudy, "Experiments with a non-linear spectral subtractor (NSS), Hidden Markov Models and the projection, for robust speech recognition in cars," Speech Communication , vol. 11, no. 2-3, pp. 215 – 228, 1992.
- S. Kamath, and P. C. Loizou, "A multi-band spectral subtraction method for enhancing speech corrupted by colored noise," in Proceedings of International Conference on Acoustics, Speech, and Signal Processing, Orlando, USA, May 2002, vol. 4, pp. 4160 – 4164.
- M. A. Abd El-Fattah, M. I. Dessouky, S. M. Diaband F. E. Abd El-samie, "Speech enhancement using an adaptive wiener filtering approach," Progress In Electromagnetics Research M., vol. 4, pp. 167 – 184, 2008.
- S. Ogata, and T. Shimamura, "Reinforced spectral subtraction method to enhance speech signal," in Proceedings of International Conference on Electrical and Electronic Technology, 2001, vol. 1, pp. 242 – 245.
- P. Sovka, P. Pollak, and J. Kibic, "Extended spectral subtraction," in Proceedings of European Conference on Speech Process Communication, Sept. 1996, pp. 963 – 966.
- N. Virag, "Single-channel speech enhancement based on masking properties of the human auditory system," IEEE Transactions on Speech, and Audio Processing, vol. 7, pp. 126 – 137, March 1999.
- R. Martin, "Spectral subtraction based on minimum statistics," in Proceedings of European Conference on Signal Processing, U.K., Sept. 1994, pp. 1182 – 1185.
- R. Martin, "Noise power spectral density estimation based on optimal smoothing and minimum statistics," IEEE Transactions on Speech, and Audio Processing, vol. 9, no. 5, pp. 504 – 512, 2001.
- R. M. Uderea, N. Vizireanu, S. Ciochina, and S. Halunga, "Non-linear spectral subtraction method for colored noise reduction using multi-band Bark scale," Signal Processing, vol. 88, pp. 1299 – 1303, 2008.
- Sheng Li, Jian Qi Wang, and Xi Jing Jing, "The application of non-linear spectral subtraction method on millimeter wave conducted speech enhancement," Mathematical Problems in Engineering, pp. 1 – 12, 2010.
- H. Tasmaz, and E. Ercelebi, "Speech enhancement based on un-decimated wavelet packet perceptual filterbanks and MMSE-STSA estimation in various noise environments," Digital Signal processing, vol. 18, no. 5, pp. 797 – 812, Sept. 2008.
- Chao Li, and Wen-Ju Liu, "A novel multi-band spectral subtraction method based on phase modification and magnitude compensation," in Proceedings of International Conference on Acoustics, Speech, and Signal Processing, Prague, Czech Republic, May 22 – 27, 2011, pp. 4760-4763.
- L. Singh, and S. Sridharan, "Speech enhancement using critical band spectral subtraction," in Proceedings of International Conference on Spoken Language Processing, Sydney, Australia, Dec. 1998, pp. 2827 – 2830.
- Y. Ghanbari, M. R. Karmi-Mollaei, and B. Amelifard, "Improved multi-band spectral subtraction method for speech enhancement," in Proceedings of International Conference of Signal, and Image Processing, Hawaii, USA, Aug. 23 - 25, 2004.
- K. Yamashita, S. Ogata, and T. Shimamura, "Improved spectral subtraction utilizing iterative processing," Electronics and Communications, Japan, vol. 90, no. 4, pp. 39 – 51, 2007.
- K. Yamashita, S. Ogata, and T. Shimamura, "Spectral subtraction iterated with weighting factors," in Proceedings of IEEE Speech Coding Workshop, Oct. 6 - 9, 2002, pp.138 – 140.
- Sheng Li, Jian-Qi Wang, Ming Niu, Xi-Jing Jing, and Tian Liu, "Iterative spectral subtraction method for millimeter wave conducted speech enhancement," Journal of Biomedical Science and Engineering, vol. 3, no. 2, pp. 187 – 192, Feb. 2010.
- J. D. Johnston, "Transform coding of audio signals using perceptual noise criteria," IEEE Journal on Selected Areas of Communications, vol. 6, no. 2, pp. 314 – 323, Feb. 1988.
- R. M. Uderea, N. D. Vizireanu, and S. Ciochina, "An improved spectral subtraction method for speech enhancement using a perceptual weighting filter," Digital Signal Processing, vol. 18, pp. 581 – 587, 2008.
- J. Lim, "Evaluation of a correlation subtraction method for enhancing speech degraded by additive noise," IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 37, no. 6, pp. 471 – 472, 1978.


