Spectrum Sensing for Cognitive Radio Using Hybrid Matched Filter Single Cycle Cyclostationary Feature Detector

Published Online September 2015 in MECS DOI: 10.5815/ijieeb.2015.05.03

• I.    Introduction

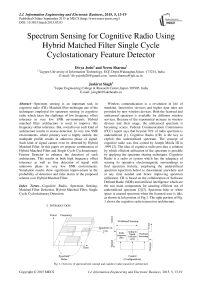
  Wireless communication is a revolution in life of mankind. Innovative services and higher data rates are provided by new wireless devices. Both the licensed and unlicensed spectrum is available for different wireless services. Because of the exponential increase in wireless devices and their usage, the unlicensed spectrum is becoming scarce. Federal Communication Commission (FCC) report says that beyond 70% of radio spectrum is underutilized [1]. Cognitive Radio (CR) is the key to exploit this underutilized spectrum. The concept of cognitive radio was first coined by Joseph Mitola III in 1999 [2]. The idea of cognitive radio provides a solution by which efficient utilization of the spectrum is possible by applying the spectrum sharing techniques. Cognitive Radio is a radio or system which has the adequacy of sensing its operative electromagnetic surroundings to find spectrum fortuity, employing the underutilized spectrum (spectrum holes) to disseminate anywhere and at any time needed and hence improving spectrum utilization. CR is based on the collaboration of Software Defined Radio (SDR) and artificial intelligence which are the two main components for assuring efficient use of underutilized spectrum [2][3]. Spectrum hole or white space is unused spectrum when the licensed user is idle, as shown in left portion of Fig.1. The right portion of Fig. 1 shows the cognitive radio transceiver architecture.

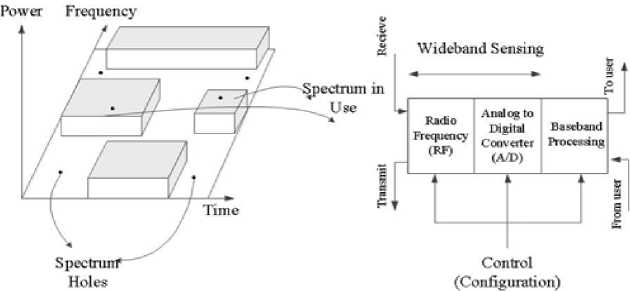
Fig. 1. Overview of spectrum hole concept and cognitive radio transceiver architecture

The main objectives of cognitive radio are as follows:

• 1.    Spectrum sensing: Determining available spectrum holes and revealing the presence of licensed users [4].

• 2.    Spectrum management: Making the adaptability of the available spectrum, huge [5].

• 3.    Spectrum sharing: Providing moderate spectrum scheduling to already allocate unlicensed users.

• 4.    Spectrum mobility: Prolong consistent transition from one spectrum hole to another.

The success of cognitive radio largely depends upon the competency of the first step of spectrum sensing in the cognitive radio cycle [4]. The spectrum sensing technique deployed by CR can be classified broadly into Non- cooperative detection (Transmitter detection), Interference based detection and Cooperative detection. Furthermore, Non-cooperative detection is classified into: Matched Filter Detection (MFD), Energy Detection (ED) and Cyclostationary Feature Detection (CFD). The focus of this paper is on Hybrid Matched Filter detection which is a kind of MFD scheme and belongs to the class of Non-cooperative sensing schemes [6]. Section II discusses the Hybrid Matched Filter (HMF) [6] and Single cycle Cyclostationary Detector [7]. In section III, the proposed work is explained. Simulation results are discussed in Section IV. Paper is concluded in section V.

• II.    Related Work

Spectrum sensing technique facilitates the efficient usage of the available spectrum. Various spectrum sensing methods are proposed in literature. [13] defines cognitive radio channel as a two-sender, two-receiver interference channel in which sender two obtains the encoded message sender one transmits. [14] considers the sensing duration to maximize the throughput for the secondary network. Energy detection scheme is used here to find the optimal sensing time. [15] explains cooperative sensing and its various forms. Also external sensing algorithms and other sensing methods are discussed. Databases and geolocation has been considered by using beacons for spectrum sensing.

In [16], the benefits of cooperation in cognitive radio are illustrated. Authors have shown that by allowing the cognitive users operating in the same band to cooperate the detection time can be reduced and thus increase the overall agility. In [17], a linear cooperation framework has been proposed. Interference to primary radio was minimized and spectrum utilization was increased. In

[18], two sensing algorithms are suggested, one is based on the ratio of the maximum eigen value to minimum eigen value; the other is based on the ratio of the average eigen value to minimum eigen value. In [19], the cognitive radio users were made to cooperate with each other in trying to detect licensed transmissions. In [20], wideband spectrum ensing technique, called multiband joint detection, which jointly detects the signal energy levels over multiple frequency bands rather than consider one band at a time. In [21], hybrid channel state acquisition schemes were considered that used cooperative multiband sensing to build a virtual spectrum database for ad hoc CR systems, which was referred as the spectrum pool.

This technique helps cognitive radio to search for the existence of primary user [4]. In Non-corporative sensing, CR exploits different kinds of features embedded in the signal of primary user to detect its presence. Energy Detection scheme uses sampled energy of the received waveform as the threshold to determine the presence of primary user [4]. The basic operation of Matched Filter is similar to the correlation function in which the signal is convolved with filter whose impulse response is time inverted version of the signal itself [4]. Therefore, it requires prior information  about the transmitted waveform by primary user. MFD cannot differentiate between signal and noise below the SNR of -20 dB. Cyclostationary Feature Detection (CFD) works on the principle that most of the man-made signals are stationary in wide sense, that is one or more of their statistics vary periodically with time [8]. Such kinds of signals are called Cyclostationary or Polycyclostationary depending on whether the statistics vary with single or multiple periodicities respectively [8]. The most commonly used statistic is the mean of the signal. Thus, if any of the statistics of the received signal is varying with either single or multiple periodicities then the primary user signal is present.

• A.    Hybrid Matched Filter

It has been proved in [4][6] that Matched Filter Detection (MFD) has the fastest sensing time among all the non-cooperative schemes till a certain low threshold value of Signal-to-Noise Ratio (SNR). After this value, sensing time increases in an unbounded fashion [9]. Also, MFD faces another problem of low frequency offset tolerance in multipath fading scenarios which renders it useless for low SNR environments [6]. Therefore, Hybrid Matched Filter (HMF) has been proposed in the literature as a solution to this problem, which has been shown in Fig. 2 [6].

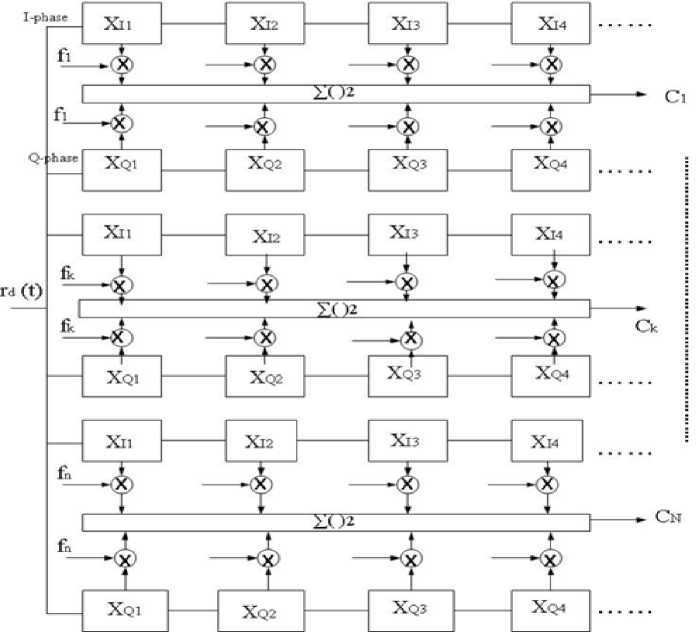
Fig.2. Structure of hybrid matched filter detector

HMF is the combination of orthogonal, parallel and segmented matched filter where each parallel branch demodulates the received signal at different residual offset frequency and there are several segments [6]. Furthermore, each segment is an orthogonal matched filter. Therefore instead of performing sequential checks on different residual frequencies to identify the correct offset, each parallel branch performs parallel check at the same time which enhances the sensing time [6][10][11]. If f is the minimum frequency offset tolerance of a matched filter then the desired frequency offset tolerance, f_TO is given by [6][10][11]:

f_TO = N eg X f min                 (1)

twofold benefit. It increases the frequency offset tolerance because increasing the sampling frequency leads to increase in N which will increase f as can seg                                TO be seen from (1). The sensing time can also be improved by over sampling at the receiver by increasing the number of samples [6][12]. Once the number of segments is fixed in order to acquire a desired frequency offset tolerance, then number of samples can be further increased by increasing the number of samples per segment [6]. Therefore, HMF also results in reduced sensing time in low SNR scenarios along with high frequency offset tolerance by deploying different parallel branches each working on certain residual offset frequency [6][10].

• B.    Single Cycle Cyclostationary Feature Detector

Where N is the number of segments in one parallel branch of HMF [10][11].

Let N be the number of samples of a transmitted waveform taken over one period during sampling. When the received signal is demodulated to baseband frequency and sampled at a certain frequency f , and then the sensing time is given by           [6][9][12]. The sampling frequency is given by:    s

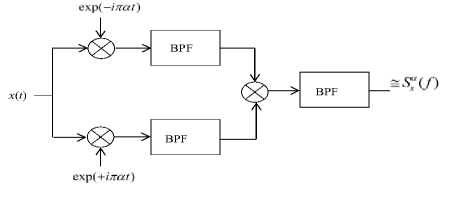
Fig. 3. Single cycle cyclostationary detector

f s = N seg ^x N s samples/sec            (2)

Where N is the number of samples per segment [11].Thus, increasing the sampling frequency has a

Gardner’s definition of cyclostationarity says that a signal is said to have cyclostationarity if the mean value of its second order delay product exhibits periodicity. The mean value of second order delay product is also called autocorrelation function [7][8]. Fig. 3 shows the single cycle cyclostationary detector. There are two approaches for the cyclostationary analysis of a signal: Stochastic as well as non-stochastic approach [8]. In this paper, focus is on stochastic approach where the received signal is modeled as a stochastic process having several sample functions. The autocorrelation function is given by:

R x ( т ) = E [ X ( t ) X ( t + т )]              (3)

where, E [ - ] is the expected value operator which is the mean value equivalent in probability space theory [8]. Furthermore, X ( t ) and X ( t + т ) are the two random variables at time instants t and ( t + т ) . Now, if the received signal exhibits cyclostationarity then the probability space autocorrelation function will be periodic in behaviour [7][8]. Since, it is known that any periodic function can be represented using Fourier series, therefore, the probability space autocorrelation function is given as [7][8]:

to

R a } = £ R “_x e^jM = R x (т )         (4)

n=-to where, Ra are the Fourier coefficients of individual X components at different cyclic frequencies, a . Furthermore, these Fourier coefficients are equal to the Cumulative Distribution Functions (CDFs) evaluated at different sampling instants [8] and hence we can re-write the above equation as:

Fa} = V F^-" = R{“}

XXX n=-to where, F^ is a Cumulative Distribution Function which is defined as [7][8]:

Fa = Prob[ X (t + т) < x ](6)

Therefore, probability space autocorrelation function can also be found out by evaluating Cumulative Distribution Function at every sample of a sampled signal [8]. If this autocorrelation function is periodic or polyperiodic then it is called cyclic autocorrelation function and shows the presence of a signal [8]. The stochastic approach to detect any cyclostationary signatures inside the received signal has been discussed in this section. This will act as a background to accomplish the signal processing operations involved in our proposed work.

• III.    Proposed Work

The desired frequency offset tolerance of Hybrid matched filter (HMF) is given by (1). Therefore, total number of samples per parallel branch of HMF is given by Л = Ntotal = Ns X Nseg , where Ntotal is the total number of samples per parallel branch of HMF and N is the number of samples per segment. Let’s say that the transmitted signal is given by:

m ( t ) = c ( t )V2 S cos(2 n f_bt + ф _м )          (7)

Where, c ( t ) is the code word waveform which is modulated over one of the M-ary PSK waveform, S is the signal power, f is the baseband frequency, ф is one of the values of M-ary phase. But because of channel impairments such as Doppler shift and Additive White Gaussian Noise (AWGN), the receiver will receive m ( t ) in the form given below:

r ( t ) = c ( t )V2 S cos(2 n f_bt + ф + 0 ( t )) + n ( t )    (8)

where, 0 (t ) is a dynamic phase due to Doppler shift which is the function of time. n ( t ) is the AWGN process. Therefore, the received signal can be represented as:

r ( t ) = c ( t )V2 S cos(2 n f_bt + ф ( t )) + n ( t )      (9)

Where, ф (t ) = ф + 0 ( t ) and is the total dynamic phase shift.

The received signal r ( t ) is then demodulated at different residual offset frequencies whose number is equal to the number of parallel branches in HMF structure, where each branch samples r ( t ) into N samples. Therefore, the demodulated received signal in branch i , rⁱ ( t ) is given by:

r d ⁽ t ) = ^{r (} t ) cos(2 ^{n ( f} b ^- fi, ) t + ^ф м ) + j sin(^{2 n} ( ^f b ^- f ) t + ^ф м ^)]

Where, f is the residual offset frequency of branch i . Furthermore, signal can be rewritten as:

i d ( t ) = [ г¹ , ( t ) + n | ( t )] + j [ r Q ( t ) + n Q ( t )]    (11)

Where, rⁱ ( t ) is the I-phase component of the received demodulated signal, nⁱ ( t ) is I-phase component of the AWGN process, rⁱ ( t ) is the Q-phase component of the received demodulated signal and nⁱ ( t ) is the Q-phase component of AWGN process.

^r I ⁽ t ) = c ⁽ t ⁾V2 ^S yo^{s[2 n f} b t + ф ⁽ t )] • cos^{[2 n (} f b ^{- f} _ri ) t + ^ф м ]    (12)

r^l Q ( t ) = c ( t )V2 S cos[2 n f b t + ф ( t )] • sin[2 n ( f_b - f_n ) t + ф _м ]    (13)

Similarly, the I-phase and Q-phase components, nⁱ ( t ) and nⁱ ( t ) respectively of AWGN process are given as:

nI (t) = n(t )cos[2^( Jb - fH ) t + фт ]

nQ(t) = n(t )sln|2-( f - f)t + Фт](15)

The received demodulated signal ri (t) is sampled at sampling instants of Ts = 1/ Ntotd which results in column vectors. Therefore, rd(Ts) = [ №) + nI (Ts)] + j [ rQ (Ts) + nQ (Ts)](16)

where, every element is a column vector. Furthermore,

Г (Т,) = [ X, (t + nTs)] + j [ XQ (t + nTs)](17)

where, X , ( t + nT_s ) and X g ( t + nT_s ) are the column vectors of Gaussian distributed random variables with mean as the corresponding elements of the column vectors rⁱ ( T ) and rⁱ ( T ) respectively and the variance is set according to desired SNR. Then the magnitude squared values of the statistic to be observed is calculated for every branch i as:

N total                                 N total

M , = £ [ X ( t + nT s )] 2 + £ [ X Q ( t + nT s )]² n = 1                             n = 1

calculated from individual columns of two dimensional vector V . Every element of C is the correlation coefficient of the corresponding branch. Hence, the received demodulated signal of branch j is selected for further processing if c. = max{ c _z} where I' ^ j .

Furthermore, the autocorrelation function, R { “ ^}( r ) of received demodulated signal of branch j is given by:

R а } ( т ) = F^ - [N( _M j, a 2, )] + zF^ a ^}[ N( ^ Q, a Q )]  (19)

where, F{0} is the Cumulative Distribution Function evaluated for the Normal Distribution N(^ a2) and F{a} is the Cumulative Distribution Function evaluated for the Normal Distribution N(^Q aJe) . The {a} in the suffix shows that it is a set which can consist of one cyclic frequency or multiple cyclic frequencies. If it consists of only one cyclic frequency as zero then primary user signal is not present. If it consists of only one cyclic frequency then primary user signal is present and cyclostationary otherwise polycyclostationary. The degree of similarity between transmitted signal and received signal is further determined by computing magnitude squared autocoherence (MSAC) value, MSAC which is given by:

MSACj

M ( f )²

r Tk f - j ) r a }k f + j )

where, M ( f )is the power spectral density of the transmitted signal. In order to perform hypothesis test on MSAC , the probability distribution followed by these values is to be determined by performing Monte Carlo simulation for large number of times.

Hypothesis test is further performed on that distribution with null hypothesis stating that only noise is present, whereas alternative hypothesis stating that primary user signal is present with a specific level of significance.

• IV.    Simulation Analysis and Results

A set of extensive simulations have been performed for both HMF and the proposed scheme on Matlab. The performance is evaluated in terms of probability of detection and probability of false alarm. The prominence is to evaluate the comparative performance of HMF and the proposed scheme. In the performed simulations, the number of samples per segment has been set to four.

To determine the distribution followed by magnitude squared autocoherence value, an extensive set of Monte Carlo simulations for different values of SNR have been performed for 1000 iterations and it came out to be lognormal distribution for the case when primary user signal is present.

During the actual simulations, each computed value of magnitude squared autocoherence have been put through hypothesis test on the log-normal distribution of generated magnitude squared autocoherence values at a significance level of 0.15. The null hypothesis in the test is the absence of signal whereas the alternative hypothesis is the presence of the signal.

Fig. 4 demonstrates higher probability of detection of the proposed scheme in comparison to the HMF. This is because the algorithm selects the highest value of correlation coefficient from all the corresponding correlation values of individual branch. This highest value is the indicator that the residual offset frequency of the corresponding branch used in demodulating the signal finds perfect correlation with the Doppler phase shifted received signal due to multipath profile. This provides the coarse detection that some signal has been detected whose phase shift actually correlates well with one of the residual offset frequencies. Then the demodulated signal using that residual offset frequency is sent to the cascaded stage of processing where it becomes further processed using single cycle Cyclostationary Feature Detector. Therefore, due to this cascaded stage of Cyclostationary Feature Detector, the course detection becomes finer; hence there is little chance of being a miss detection.

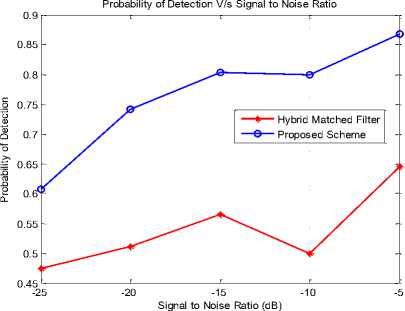
Fig. 4. Probability of detection for combined hybrid matched filter single cycle cyclostationary detection

Since, the probability of detection increases therefore, the probability of false alarm reduces. Fig. 5 depicts the same trend in the probability of false alarm for the proposed scheme as well as HMF. The probability of false alarm for proposed scheme is much less than that of HMF.

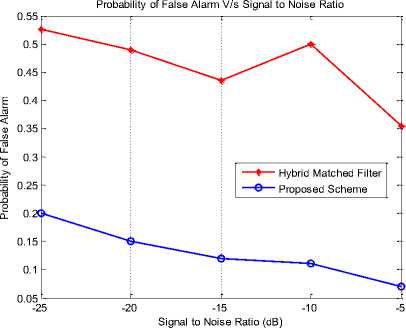
Fig. 5. Probability of false alarm for combined hybrid matched filter single cycle cyclostationary detection

• V.    Conclusion

Simulation results depict significant improvement in the probability of detection and probability of false alarm in case of proposed scheme over HMF. Hence, the proposed scheme clearly outperforms HMF in terms of both metrics. But the proposed scheme incurs significant overhead in terms of execution time involved in the signal processing related to cascaded stages. Therefore, it would be interesting to reduce the execution time of the proposed scheme.