Speech Compression Based on Discrete Walsh Hadamard Transform

Published Online September 2013 in MECS DOI: 10.5815/ijieeb.2013.03.07

Speech compression is a ripe subject of research. It is a necessity to satisfy the transfer requirements of speech signals via channel communication or storage device. The speech compression has many applications such as; multimedia applications and satellite communications.

The compression techniques can be broadly divided into two classes: lossless and lossy compression. The lossless compression which means that when speech is decompressed, the original data will be restored without any modification, however, the lossy compression does not allow the exact original data to be reconstructed for the compressed speech.

The compression methods can be classified into three functional categories [1]: the first is compression by direct method; the samples of the speech signal are directly handled provide compression. The second is compression by transformations such as; Discrete Cosine Transform (DCT), Discrete Fourier Transform (DFT) and Discrete Wavelet Transform (DWT). The third method is compression by parameters extraction; the input speech signal is analyzed to extract some parameters that are later used to reconstruct the signal.

During last decade, the DWT has emerged as a powerful mathematic tool for speech processing such as; audio/image compression [1], [2], [3], [4], [5] and denoising [6], [7]. The performance of speech compression by the DWT is very good compared with other techniques [2], [3] such as DCT used in MPEG (Moving Picture Experts Group) and JPEG (Joint Photographic Experts Group) and especially for non-stationary signal. However, for real-time processing the DWT present a high complexity implementation.

In above context, this paper presents a speech compression algorithm for stationary signal based on Discrete Walsh Hadamard Transform (DWHT). The proposed algorithm is characterized by a very low complexity implementation and improved compared to DWT technique.

The paper is organized as follows. Section 1 covers the Discrete Walsh Hadamard Transform theory. Section 2 presents a brief introduction for wavelet theory. Section 3 attempts to explain the methodology for speech compression using DWT and DWHT. Section 4 shows the results. Finally, section 5 gives conclusion and remarks.

• II.    Discrete Walsh Hadamard Transform

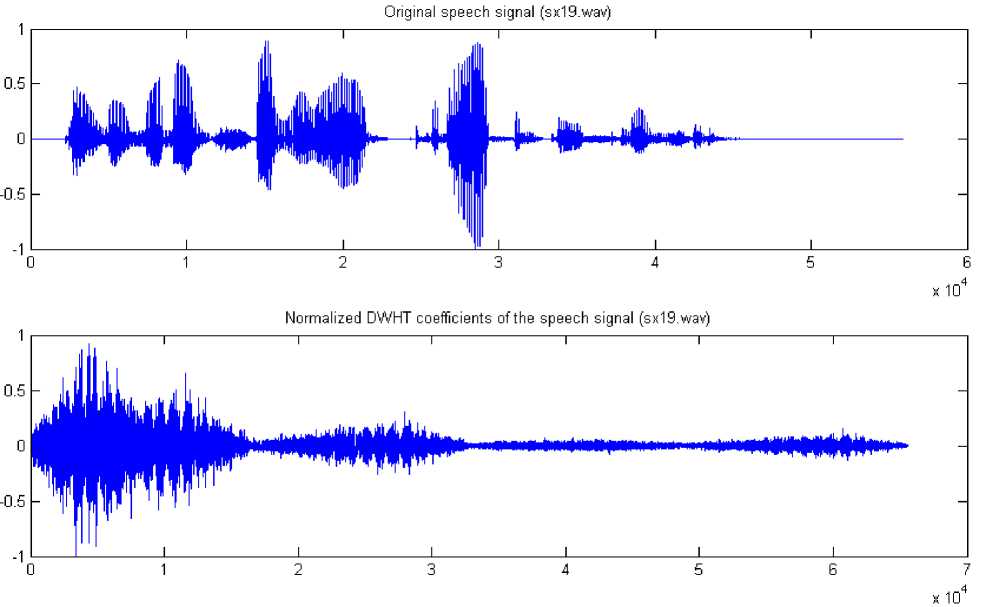
The Discrete Walsh-Hadamard transform (WHT) is an orthogonal transformation that decomposes a signal into a set of orthogonal, rectangular waveforms called Walsh functions [8], [9]. The Hadamard transform take only the binary value +1 or -1. The direct and inverse DWHT pair for a signal x(t) of length N are respectively expressed as follow:

Where, b ( n ) is the i^th bit in the binary representation of x ( n ) with r bits and p ( k ) is computed using [1]:

P o ⁽ k ) = b r - 1 ^{( k} )

У(n) = — ]Tx. WAL(n,i) n = 1,2,....,N-1 N~0

P 1 ^(k ) = b r - 1 ^{( k} ) ⁺ b r - 2 ^{( k} )

N - 1

X = Z y(n) WAL(n, i) n = 1,2,...., N-1      (2)

n = 0

P , ^{( k} ) = ^b, - 2 ^{( k} ) + ^b, - 3 ^{( k} )

x(n) and y(n) are respectily the original and reconstructed speech signal.

P r - 1 ^{( k} ) = ^b 1 ^(k ) + ^b o ^{( k} )

.

v^-' i = r —1

WAL ( n , i ) = ( - 1 )^Z i =o b i^{( n} ) ^{p - (} k )                        (3)

• III.    Discrete Wavelet Transform

The Discrete Wavelet Transform (DWT) is a powerful mathematic tool for time-frequency analysis of non-stationary signals. It uses multi-resolution filter banks for the signal analysis. The general form of DWT at L-level is written in terms of L detail coefficients d(k), and the Lth level approximation coefficients c(k) can be expressed as [5]:

L

f (t ) = Z cL ( k ) ФL ( t ) + ZZ dj ( k X ( t ) k                      j=1  k

Where, the functions ф ( t ) and ф ( t ) are respectively known as the scaling function and the mother wavelet. The approximation and detail coefficients at level j are given by:

C j + 1 ( k ) = Z h o ( m - 2 k ) C ( m )                 (6)

m dj+i(k) = Z hi(m — 2k) C (m)               (7)

m

h ( k ) and h ( k ) are known as wavelet filters.

• IV.    Methodology for Speech Compression

In this research work, speech compression algorithm based on transformation is performed using three most commonly used steps: applying transformation (DWHT or DWT), truncate coefficients (thresholding) and quantization followed by entropy encoding (Figure 2).

the largest absolute value coefficients. In this case, the threshold value ( thr ) is manually adjusted and is chosen from coefficients ( 0 <  thr <  C_{KalM ax} ), where C is the maximum value of the DWHT coefficients or DWT Coefficients.

Step3: Signal compression using transformation is achieved by truncated small valued coefficients and efficient encoding them. There are many way to encode coefficients; one way, is to store the thresholded coefficients with their respective positions in the DWHT vector [1]. In this work, for encoding coefficients, the consecutive zero valued coefficients are encoded with two bytes: One byte to indicate the start sequence of zeros in the coefficients vector and the other byte is used to represent the number of consecutive zeros (example: Figure 1) [2]. After encoding coefficients, a quantization process (Uniform, scalar or vector quantization) is performed followed by an entropy encoder (Huffman or arithmetic coding) to eliminate any redundancy caused by quantization.

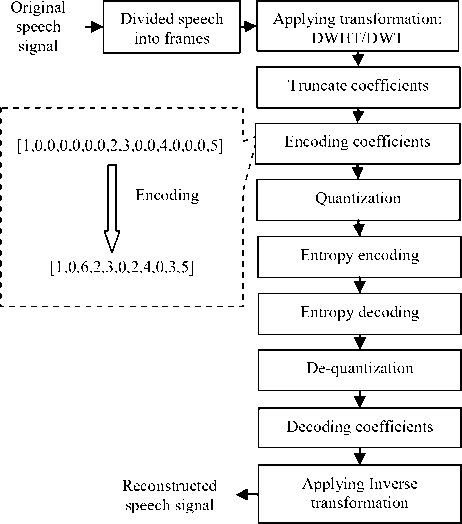
Fig. 2: Discrete Walsh Hadamard Transform based methodology for speech compression

• V.    Tests and Results

In this section, a MATLAB program has been developed for implement the speech compression codec based on DWHT described in this paper. To evaluate the efficiency of the developed algorithm a comparative performance study between the DWHT and DWT algorithms given in [1], [2], [3] and [4] used for speech compression is made in terms of: computation time (CPU time), Compression Ratio (CR), Signal to Noise Ratio (SNR), Peak Signal to Noise Ratio (PSNR) and Normalized Root Mean Square Error (NRMSE). In the simulation steps, all used source waveform files are taken from TIMIT Database, sampled at 16 kHz.

The obtained results are calculated using the following formulas:

■ Signal to Noise Ratio (SNR):

SNR =

Z x (n )2

Zlx(n) - y(n )I2

■ Peak Signal to Noise Ratio (PSNR) :

Step1: In this step, the input speech signal is divided into stationary frames and then transformation method (DWHT or DWT) is applied of each frame in order to extract coefficients.

Step2: After performing the transformation method of the speech frame, com41pression involves truncating the obtained coefficients below a given threshold values. For truncate the small valued coefficients, a global thresholding is applied. It’s consists in taking the obtained coefficients for each speech frame and keeping

PSNR = 10log10

Nx (n )2

J|x(n)- y(n)||2 ?

■ Normalized Root Mean Square Error (NRMSE):

PSNR = 10log10

Nx (n )2

J Iх (n)- y(n )||2

• Compression Ratio (CR):

size of original signal

size of compressed signal

Where, x(n) and y(n) are respectively the original and the reconstructed speech signal, N is the length of the reconstructed speech signal and Ц (n) is the mean of the speech signal.

Table 1 and figure 3, illustrate the performance evaluation of the proposed algorithm for speech compression based on DWHT.

Table 1: Performances evaluation using DWHT for speech compression

Source waveform files	Threshold values	CR	SNR	PSNR	NRMSE
sx19.wav	0.0027	4.5028	18.0160	39.1079	0.1257
sx27.wav	0.0028	4.2140	18.1416	39.0820	0.1239
sx29.wav	0. 0009	8.0193	24.3324	51.3917	0.0607
sx30.wav	0.0022	3.7276	18.5287	39.1578	0.1185
sx37.wav	0.0027	4.2200	19.6431	38.5735	0.1042
sx41.wav	0.0016	3.5660	18.3578	42.7530	0.1208
sx46.wav	0. 0028	4.0968	18.1045	39.1243	0.1244
sx56.wav	0. 0020	3.0804	18.0620	40.6448	0.1250
sx63.wav	0. 0025	3.6526	17.0268	38.6134	0.1408
sx77.wav	0. 0027	4.1803	18.6579	38.8914	0.1167
sx81.wav	0.0025	5.4464	18.8741	40.2100	0.1138
sx87.wav	0. 0028	3.4364	19.0717	37.9964	0.1113
sx93.wav	0.0030	4.3077	17.7421	38.1067	0.1297

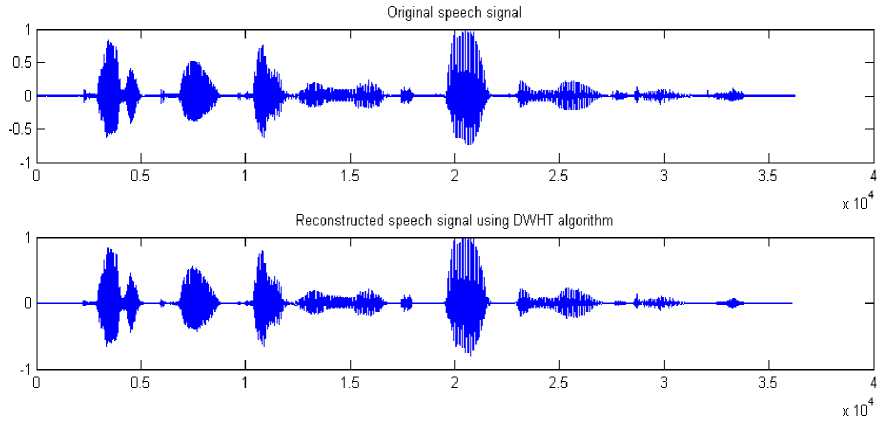
In the simulation steps, the speech signal is divided into frames of size 256 and global thresholding is applied. From the table 1, it is clear that the developed algorithm based on DWHT provides an important compression ratio while keeping a good quality of the reconstructed speech signal. Figure 3 illustrates the plot of original and reconstructed speech signal (“Critical equipment needs proper maintenance”) using DWHT algorithm.

Table 2 illustrates the comparative performance of the proposed algorithm and the algorithm based on based on DWT. For the DWT algorithm given in [2], [4], [5] and [6], the used mother wavelet is “db10”, five decomposition levels and global thresholding are applied.

Table 2: Comparison of performance between DWHT and DWT

Source waveform files	Algorithms	Threshold values	CPU Time (s)	CR	SNR	PSNR	NRMSE
sx19.wav	DWT	0.0650	3.7969	3.9789	18.2507	39.3426	0.1223
	DWHT	0.0025	1.3750	4.2609	18.5368	39.6287	0.1183
sx27.wav	DWT	0.0600	2.5156	3.5111	18.6414	39.5818	0.1169
	DWHT	0.0025	0.8125	3.9672	19.0219	39.9624	0.1119
sx30.wav	DWT	0.0520	1.9375	3.1525	18.3430	38.9721	0.1210
	DWHT	0.0022	0.6719	3.7276	18.5287	39.1578	0.1185
sx31.wav	DWT	0.0430	2.6406	2.7657	17.6014	39.5243	0.1318
	DWHT	0.0022	0.8906	3.2498	18.0094	39.9323	0.1258
sx34.wav	DWT	0.0400	4.6094	2.5369	18.5023	40.4045	0.1188
	DWHT	0.0021	1.6250	2.9132	18.7166	40.6188	0.1159
sx37.wav	DWT	0.0620	2.6563	3.6009	19.7017	38.6321	0.1035
	DWHT	0.0027	0.9063	4.2200	19.6431	38.5735	0.1042
sx38.wav	DWT	0.0365	4.2188	3.1461	18.8678	42.0462	0.1139
	DWHT	0.0017	1.5156	3.4667	18.9621	42.1406	0.1127
sx81.wav	DWT	0.0650	2.3594	4.4344	18.7374	40.0733	0.1156
	DWHT	0.0025	0.7969	5.4464	18.8741	40.2100	0.1138

From the above table , it is evident that the total CPU time (in seconds) used by MATLAB for running DWHT algorithm is decreased to about 65,5% compared to the DWT algorithm. In addition, it can be seen that the global performances (CR, SNR, PSNR and NRMSE) are significantly improved.

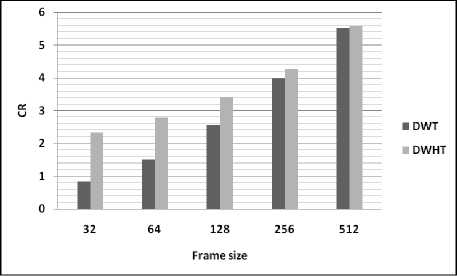
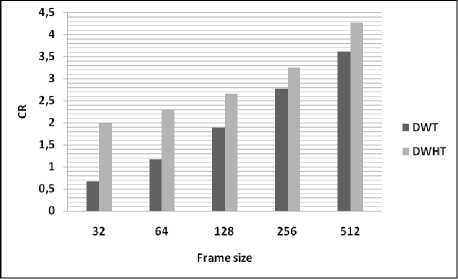
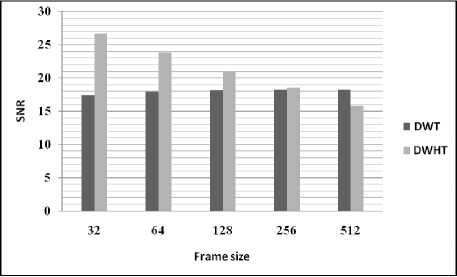
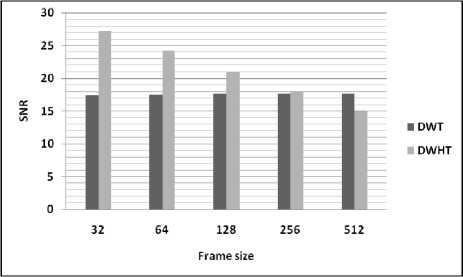
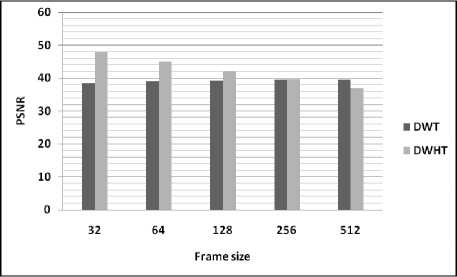
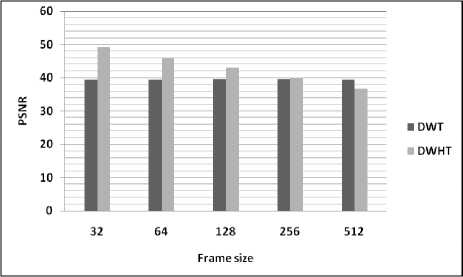
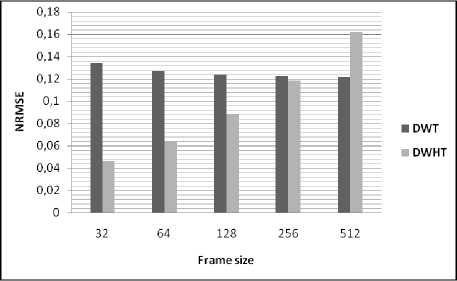
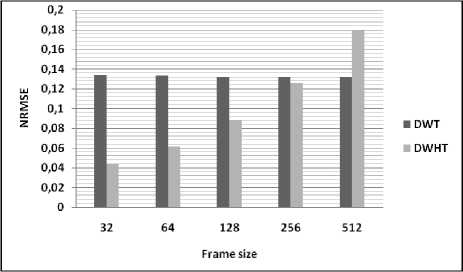
Table 3 and figures, illustrate the variation of performances study of the developed based on DWHT for different values of frame size. From the figures, it can be seen that the quality of the reconstructed speech signal using the proposed algorithm is degraded for large frame size (non-stationary signal).

Table 3: Comparison of performance using different values of frame size

Source waveform files	Mesures	Algorithms	Frame size
			32	64	128	256	512
sx19.wav	CR	DWT	0.8370	1.5044	2.5510	3.9789	5.5215
		DWHT	2.3230	2.7883	3.4113	4.2609	5.5861
	SNR	DWT	17.4444	17.9365	18.1304	18.2507	18.2806
		DWHT	26.6662	23.8570	21.0363	18.5368	15.8379
	PSNR	DWT	38.5438	39.0334	39.2223	39.3426	39.3726
		DWHT	47.7656	44.9539	42.1282	39.6287	36.9299
	NRMSE	DWT	0.1342	0.1268	0.1240	0.1223	0.1219
		DWHT	0.0464	0.0641	0.0888	0.1183	0.1615
sx31.wav	CR	DWT	0.6683	1.1713	1.8898	2.7657	3.6109
		DWHT	1.9829	2.2825	2.6595	3.2498	4.2784
	SNR	DWT	17.4669	17.4930	17.5950	17.6014	17.5889
		DWHT	27.2253	24.1645	21.0686	18.0094	14.9258
	PSNR	DWT	39.4159	39.4383	39.5328	39.5243	39.4818
		DWHT	49.1743	46.1098	43.0064	39.9323	36.8186
	NRMSE	DWT	0.1339	0.1335	0.1319	0.1318	0.1320
		DWHT	0.0435	0.0619	0.0884	0.1258	0.1794

(a)

(e)

(b)

(f)

(c)

(g)

(d)

(h)