Спектральная плотность мощности доплеровского рассеивания (ДСПМ) сети Vanet

VANET – это система связи с подвижными объектами. Существующие модели каналов не могут учитывать временные изменения характеристик в данной сети. В связи с этим необходимо провести анализ этих параметров для канала связи с подвижными объектами.

Для начала определим что есть эффект Доплера. Эффект Доплера – это изменение частоты, и, соответственно длины волны излучения, которое воспринимается наблюдателем (приемником) вследствие движения источника излучения и/или движения наблюдателя (приемника) [1].

VANET сети характеризуются подвижностью узла, что делает среду распространения сигнала подверженной изменениям во времени и затуханиям. Как следствие, статистические характеристики принимаемого сигнала непрерывно изменяются, что приводит к возникновению эффекта Доплеровского рассеивания [2].

Большинство исследований направленных на моделирование канала связи с подвижным источником и подвижным приемником (Mobile-to-Mobile link – M2M) [3] в основном касаются детерминированных моделей беспроводных каналов. В этих моделях скорость узла предполагается постоянной на всем участке пути и статистические характеристики принимаемого сигнала, как предполагается, фиксированы во времени. Спектральная плотность мощности Доплера так же постоянна в течение каждого момента времени. Но в действительности среда распространения непрерывно изменяется из-за подвижности узлов с различными скоростями, что влияет на динамическое изменение топологии сети, на изменение угла падения волны на приемник. В реальных условиях работы системы характеристики канала распространения радиоволн меняются во времени вследствие перемещения передатчика и/или приемника и окружающих объектов. В результате, современные модели, предполагающие неподвижность статистических характеристик канала, больше не могут охватывать и отслеживать сложные изменения времени в канале распространения радиоволн.

В зависимости от скорости мобильных узлов, длины волны доплеровские сдвиги частот могут привести к ДСПМ. ДСПМ канала связи VANET для полученного затухания частоты f выглядит как [4]:

5 ( f ) pG / n f.

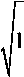
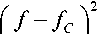
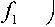
I f - fc\< f,

0, otherwise где f - максимальная частота Доплера подвижного узла; p - средняя мощность, получаемая изотропной антенной; G - усиление приемной антенны.

Для канала связи VANET, у которого f и f - это максимальные частоты Доплера передатчика и приемника, соответственно, степень двойной подвижности, обозначаемая как а , определяется формулой:

а =

min (f.-f2)

max ( f , ^f , ) ^-

причем для коэффициента а выполняется условие: 0 <  а <  1 , где а = 1 соответствует полной двойной подвижность узлов, а а = 0 соответствует подвижности одного объекта так же, как в сотовой связи, подразумевая, что каналы сотовой связи являются частным случаем M2M канала связи.

Соответствующая детерминированная ДСПМ для канала связи VANET представляется в виде [2, 40]:

f                     2

,5(f>  г=f     V-(Tf) -If- f^ <(1+а)fm,

m

(pG)/ п fm а    <7

0, otherwise где K(•) - полный эллиптический интеграл первого порядка; f = max(f, f).

На рис. 1 изображена ДСПМ для канала связи VANET для различных значений коэффициента а . Таким образом, был определена ДСПМ для канала связи с подвижными объектами, в которой U-образный спектр для канала сотовой связи является частным случаем.

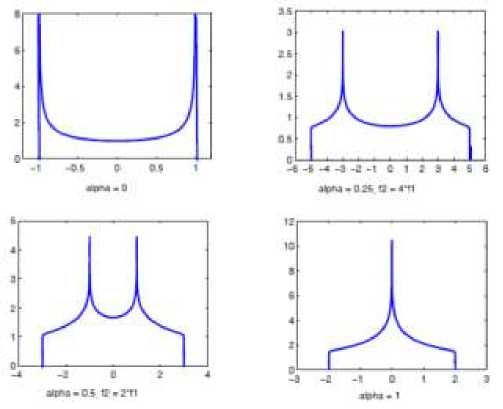
Рис. 1 - Спектральная плотность мощности Доплера для канала связи VANET для различных значений коэффициента а .

Из графиков видим, что ДСПМ для каждого значения а симметрична относительно нуля, максимумы функции сближаются при увеличении а , а при а = 1 максимумы сливаются.

Из представленных выше спектров для анализа выберем ДСПМ для коэффициентаа = °-5. Определение спектральной плотности мощности Доплера по формуле (3) является крайне затруднительным, так как полный эллиптический интеграл первого порядка невозможно вычислить в общем виде не численными методами.    Тогда для определения ДСПМ воспользуемся численным интегрированием по методу Симпсона или методом парабол. Формула Симпсона имеет вид:

B              Ъ (              n                 n — 1

J f ⁽ х ) dx = - f ⁽ x ₀) + 4 ^ f (x₂ i - 1 ) + 2 ^ f (x₂ i ) + f ⁽ X 2 n ) ,                      ⁽⁴⁾

A               ³ V               i = 1                   i = 1                        )

• 1    B - A где h =--шаг интегрирования, n - число элементарных участков.

• 2    n

Максимально увеличив масштаб фигуры спектральной плотности мощности Доплера канала связи VANET для коэффициента а = 0.5 , по формуле численного интегрирования (4) найдем площадь этой фигуры и умножим на x², тогда получим ДСПМ в виде:

B

J x ²[ S ] dx

A где B = (1 + a)fm, A = -B - пределы интегрирования, S - площадь фигуры.

Так как фигура симметрична относительно нуля, то вычисление площади мы будем производить на половине фигуры, а затем увеличим полученную площадь вдвоем. Разобьем фигуру на 22 равных элементарных участка и определим по вертикальной шкале уровень пересечения каждого участка с фигурой (рис. 2).

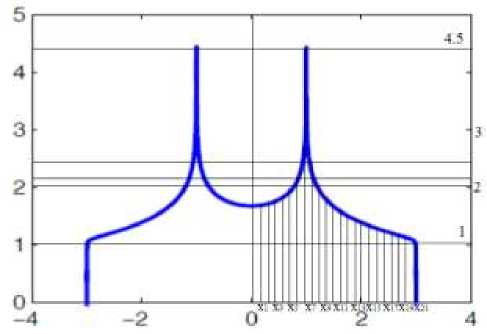
Рис. 2 – Разбиение фигуры на элементарные участка для выполнения численного интегрирования по методу Симпсона для а = 0.5

Произведем расчет спектральной плотности мощности Доплера для

степени двойной подвижности а = 0.5 .

• 1.    Определим пределы интегрирования для формулы (5). Так как степень двойной подвижности а = 0.5 , то максимальная частота Доплера приемника f должна быть в два раза больше максимальной частоты Доплера передатчика f , тогда примем f = 300 [ Гц ] , f = 600 [ Гц ] , отсюда f m = 600 Гц:

' B = (1 + а )£„ = (1 + 0.5) • 600 = 900

• \ A = - в = - 900

  , B - A h =

  2 n

  
  

  4.5 - 0

  2 • 22

  
  

  = 0.102

  
  

L f             22                  ²¹

S = 2 • h I f ( x 0 ) + 4 ^ f (x ₂ i J + 2 £ f (x ₂ i ) + f ( x 2 n )

• ³    V                 i = 1                      i = 1

• 4 . Подставим полученное значение S в (5) и получим ДСПМ для канала связи сети VANET для степени двойной подвижности а = 0,5 :

h

= 2 •-( f (x0) + 4 • (f (xi) + f (x3) + ••• + f (x21)) + 2 • (f (x2) + f (x4) + ••• + f (x22))) = 8-151

J x ² [ S ] dx = | 8_151 x ² dx = 3-961 •Ю ⁹ [ В² I Гц ] . A              - 900

Таким образом, мы произвели расчет спектральной плотности мощности доплеровского рассеивания для случая с одним подвижным объектом, когда максимальная частота Доплера приемника f в два раза больше максимальной частоты Доплера передатчика f в сети связи VANET путем численного интегрирования по методу Симпсона. При наличии эффекта доплеровского рассеивания спектра сигнал принимается с «размазанным» спектром вблизи несущего колебания из-за возникновения в канале межканальных помех. Интерпретируя к OFDM сигналу, заметим, что при эффекте Доплера уход частоты в меньшую или большую стороны объясняется разностью взаимных радиальных скоростей передатчика и/или приемника и отражателей. В результате за время регистрации сигнала в приемнике происходит суммирование прямого сигнала (при его наличии) и всех отраженных, а спектр итогового сигнала становится «размазанным».

Для улучшения качества работы систем радиосвязи, использующих подобные сигналы, необходимо применять алгоритмы оценки и компенсации смещения частоты несущей при высоких скоростях движения узлов. В ситуации приближенной к реальной, система связи будет работать при наличии множества отражателей, поэтому необходимо использовать алгоритмы оценки Доплеровского рассеивания спектра для повышения помехоустойчивости канала связи.