Спектральная зависимость эффекта фотонного увеличения одномерных электронов при фотоионизации, водородоподобных примесных центров в сильном магнитном поле
Автор: Киндаев А.А., Кревчик В.Д.
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Теоретическая физика
Статья в выпуске: 3, 2007 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14718881
IDR: 14718881
Текст статьи Спектральная зависимость эффекта фотонного увеличения одномерных электронов при фотоионизации, водородоподобных примесных центров в сильном магнитном поле
Приложенное вдоль оси квантовой проволоки (КП) магнитное поле может существенно изменять ее латеральный геометрический конфайнмент. Поэтому, варьируя величину магнитного поля, можно эффективно управлять ее оптическими и транспортными свойствами [1; 2], что открывает возможности создания на основе легированных КП детекторов лазерного излучения с управляемой чувствительностью [3]. Необходимо также отметить, что исследование спектральной зависимости эффекта фотонного увлечения (ЭФУ) позволяет определять энергетическую зависимость времени релаксации и, следовательно, выявлять вклад различных механизмов рассеяния носителей заряда.
В настоящей работе развита теория ЭФУ при фотоионизации водородоподобных примесных центров в полупроводниковой структуре в виде цепочки из туннельно-несвязанных КП, помещенной в сильное продольное магнитное поле, с учетом дисперсии радиуса КП, а также с учетом спиновых состояний локализованного электрона.
Рассмотрим КП, находящуюся в продольном по отношению к ее оси магнитном поле и содержащую мелкий водородоподобный примесный центр (ВПЦ). Предположим, что ВПЦ расположен на оси КП в ее центре. Векторный потенциал А продольного по отношению к оси КП магнитного поля с индукцией В выберем в симметричной калибровке, который в цилиндрической системе координат (р, ф, z) ось z совпадает с осью КП, начало координат находится в центре КП) будет иметь вид:
Bp sin ф Bp cos р q ^ ” 7 2
Для описания одноэлектронных состояний в КП используем параболический потенциал конфайнмента:
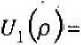
т* toyрг
где т? — эффективная масса электрона;
№0 2t70 /(m*L2)— характерная частота удерживающего потенциала КП; UQ ^ амплитуда удерживающего потенциала КП; Lx — радиус КП.
Кулоновский потенциал ВПЦ имеет вид:
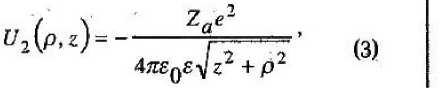
где ZQ — зарядовое число остова ВПЦ; е — элементарный заряд; ф, ™ электрическая постоянная; е — диэлектрическая проницаемость материала КП,
В случае сильного магнитного поля, ког да магнитная длина ав rJa /(т*шв^
(й = А/(2л) — приведенная постоянная Планка; шд — циклотронная частота) много меньше эффективного боровского радиуса ad (а^ « аД, кулоновский потенциал (3) можно считать эффективно одномерным и записать в следующем виде:
4ж0ф|
Можно показать, что в данном случае волновые функции Wn п т s (p.^,z) и энергети-
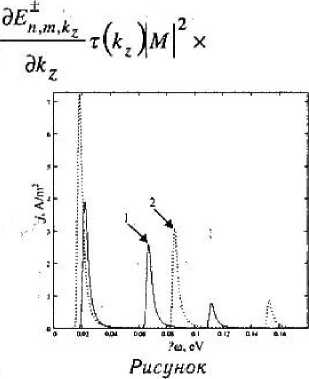
ческий спектр Efwl1 ВПЦ, имеют соответственно вид: где Lz — длина КП; й. — проекция квази волнового вектора электрона на ось z; Ф (а, у, х) — гипергеометрическая функция. ± ^П, Г^ПМ Р , 2 4а 1 И .^ С. 2 \ 2а Г X xiz exp - X /I X Л ехр( im <р ) .2 .2 2 Е„ я ™ „ = —- " (2п + ‘М + 1 н--- " m — ™ "т ту ± В r§B n,n2,m,s * 2 V 2 - * 2 * z ( у ° 2m a, 2m ав 2m а^ (n2 +1) где п,, п„ = 0,1,2,...; %2 = 2Zs/ad, at = ^/(m*Qj; — гибридная длина; £2 = ^4щ2 + (Од — гибридная частота; ь”(х) полиномы Лагерра; цЕ — магнетон Бора; g — гиромагнитное отношение. Волновые функции Фп.^Хр-Ф’^) квази-, 4- непрерывного спектра Еп т х имеют вид; 1/2 Примесный ЭФУ одномерных электронов обусловлен поглощением света с волновым вектором q =(0, 0, qz) (единичный вектор поляризации еАг перпендикулярен оси КП). Эффективный гамильтониан взаимодействия HjntB электронов с полем световой волны поперечной поляризации при наличии магнитного поля имеет вид: 2 * * 2лЯ а / х Н1П1Д = -(’М01—ч—Z0 exp(^,z)x V m <х> ± Й1 6м! и р2 2 2a,2 Г Н ет^ 2< х X COS л где \ 3 1 / , Э ieB , -Ф)~ + — sin^ti* -ф)— - — psin^-e др р ' д<р lh v Zq — коэффициент локального поля; постоянная тонкой хгехр(^.г)ф У 1 ±i---,2;-2ik.z 2к, exp^im(p ) En,m,$ =—Tl-(2n + |m| + l)+ 2m a, структуры с учетом статической относительной диэлектрической проницаемости е; с — скорость света; t0; to — интенсивность и частота поглощаемого излучения соответственно; 9 — полярный угол единичного вектора поперечной поляризации e.f Как показывают расчеты матричных элементов, из основного состояния ВПЦ возможны переходы в состояния квазинепрерывного спектра КП только со значениями магнитного квантового числа m = ±1. Выполним расчет плотности тока увлечения (ТУ) в планарной структуре из туннельно-несвязанных КП, помешенной в сильное продольное магнитное поле. Будем считать, что данная структура выполнена на основе КП, радиус Lt которых подчиняется нормальному закону распределения —7= exp ~ сгу2л Io1 , (10) где L — средний радиус КП, 6 — среднеквадратическое отклонение радиуса КП L от L, В режиме короткого замыкания плотность ТУ электронов /(ш) в планарной структуре из туннельно-связанных КП, помещенной в продольное магнитное поле, с учетом дисперсии радиуса КП имеет вид: Спектральная зависимость плотности тока увлечения /(су) при фотоионизации водородоподобных примесных центров в планарной структуре туннельно-несвязанных КП, помещенной в сильное продольное магнитное поле, с учетом спиновых состояний электрона и дисперсии радиуса КП приведена на рисунке. Как можно видеть, учет спиновых состояний приводит к дополнительному расщеплению каждого из пиков т = -I и т = +1 на два, что обусловлено параллельной и антипарал-лельной ориентацией спина электронов относительно направления внешнего магнитного поля, но так как два из них накладываются ДРУГ мый на друга, то наблюдается так называе-триплет Зеемана. 2e^ ^x^^Lx й2 dL d J XX к. л т xsUi-E*! X /?,Л|,#£ ^0,0,0 /^г где Ц — длина цепочки КП; d=2LiVNgad — период структуры (No >10 — целое число), т(йг) — время релаксации. При исследовании ЭФУ будем считать, что основным механизмом рассеяния является рассеяние на продольных акустических фононах матрицы, и исцользуем для времени релаксации результаты работы [4] в случае низких температур. Выражение для плотности ТУ примет вид: (И) Спектральная зависимость плотности тока увлечения для планарной структуры туннельно-несвязанных КП на основе InSb при Л* = 3, L = 1 mkm, Uo - 0,2 eV, L = 50 пт, Lz = 100 mkm, Z^—l для различных значений величины индукции магнитного поля 1 - 5 Т; 2 - 8 Т. La+AL^ f dLv U-kU " d X 5 ш=-1 Х-^*в~та -2/3 w + lx x +2 z , _ _9 2.4 -2 10 . ,2 *-3 -4 -J -1 где Д - 3 ■ 2 К h а0 / еЦХ^а lQm ad Ed с -1 2 а0е У X=hto/Ed, 2- _ I--"ов ~ |йо,о,о /Ed, a*=aBiad, w 2 ’-4 а T - ЦдВ i E^, + — 1 / ^— *—2 "1 — ^- = а8 \Х - Г[уВ - ma -ip w+yg. Рисунок иллюстрирует также динамику спектральной зависимости плотности тока увлечения при изменении магнитного поля. «Размытие» пиков связано с дисперсией радиуса КП в планарной структуре. Найдено, что пороговое значение плотности тока увлечения зависит от гиромагнитного отношения, а расстояние между пиками в спектре определяется циклотронной частотой. Таким образом, появляется возможность управления порогом ЭФУ, величиной плотности тока увлечения, а также расстоянием между пиками в спектральной зависимости.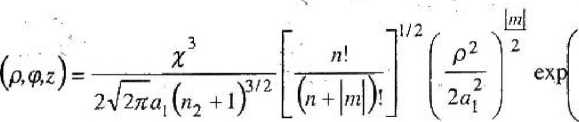
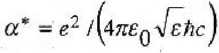
Список литературы Спектральная зависимость эффекта фотонного увеличения одномерных электронов при фотоионизации, водородоподобных примесных центров в сильном магнитном поле
- Кревчик В. Д. Магнитооптика квантовых нитей с 0(-)-центрами / В. Д. Кревчик, А. Б. Грунин, М. Б. Левашов, М. Б. Семенов // Оптика, оптоэлектроника и технологии: Тр. междунар. конф. Ульяновск: Изд-во УлГУ, 2002. С. 36. , 2. Гейлер В. А. Проводимость квантовой проволоки в параллельном магнитном поле / В. А. Гейлер, В. А. Маргулис // ФТП. 1999. Т. 33. Вып. 9. С. 1141.
- Кревчик В. Д. Эффект увлечения одномерных электронов при фотоионизации 0(-)-центров в продольном магнитном поле/В. Д. Кревчик, А. Б. Грунин//ФТТ. 2003. Т. 45. Вып. 7. С. 1272.
- Поклонский Н. А. О температурной зависимости статической электропроводности полупроводниковой квантовой проволоки в изоляторе/Н. А. Поклонский, Е. Ф. Кисляков, С! А. Вырко//ФТП. 2003. Т. 37. Вып. 6. С. 735.


