Спектральное и спектрально-модовое кодирование сигналов в оптоэлектронных преобразователях перемещения с волоконно-оптическими каналами передачи информации

Современные достижения в области микроэлектроники и информационных технологий позволяют значительно улучшить метрологические и эксплуатационные характеристики оптоэлектронных преобразователей угловых и линейных перемещений (ОПП) за счет усовершенствования вторичных преобразователей – электронных блоков (ЭБ), выносимых, как правило, в комфортные условия эксплуатации [1-3]. При этом сбор оптических сигналов от удаленных высоконадежных оптомеханических сенсоров может осуществляться по волоконно-оптическим линиям связи (ВОЛС) с последующим фотоэлектрическим преобразованием, формированием и обработкой цифровой информации в ЭБ. В современных системах передачи информации по ВОЛС возможны различные методы модуляции и кодирования сигналов: пространственное, волновое (спектральное), временное, поляризационное, модовое и их комбинации [1-5]. Практический интерес с точки зрения простоты реализации и низкой стоимости комплектующих представляет спектральная и спектрально-модовая модуляция и кодирование параметра перемещения.

Общая характеристика элементов спектральной модуляции и кодирования

Для формирования и управления спектральным составом оптических сигналов в ОПП широко применяются оптические фильтры различной структуры [2].

Рис. 1. Структурная схема МОС

На рис. 1 в качестве примера представлена структурная схема многокомпонентной оптронной структуры (МОС) спектрального взаимодействия элементов ОПП, в котором на поверхность источника излучения (ИИ), элементов оптической системы (ОС) и приемника излучения (ПИ), наносится ряд компонент (оптических фильтров) 2, 3, 5, 6 в виде многослойных тонкопленочных покрытий (МТП). Эти компоненты выполняют функции спектральной, временной и пространственной фильтрации, модуляции и коммутации, реализуя заданные алгоритмы спектрального взаимодействия.

Суть алгоритмов заключается в управлении взаимным смещением спектральных характеристик МОС, направленном, в первую очередь, на достижение заданных параметров точности и стабильности преобразования. Такое управление может быть осуществлено различными путями: воздействием тепловых, электрических, магнитных и акустических полей, изменением угла падения излучения и др. [2].

Математическая модель МОС

Для построения математической модели МОС введем следующие обозначения: Ф ^*( λ , t , τ , U_Ф ), S ^*( λ , t , τ , U_S ) – абсолютные спектральные характеристики излучения ИИ, пропускания ОС и чувствительности ПИ, U_Ô , U_T , U_S – управляющие сигналы ИИ, ОС и ПИ, Ф_п ^{* i} ( λ , t , τ ), T_п ^{* j} ( λ , t , τ ), S_п ^{* k} ( λ , t , τ ) - абсолютные спектральные характеристики пропускания i, j, k -го МТП, нанесенных на поверхности ИИ, ОС и ПИ соответственно. Тогда для последовательно соединенных элементов с МТП спектральный состав излучения I ^*( λ , t , τ ) , падающего на фо-точувствительную площадку ПИ, определяется из выражения

I *(X, t ,т) ;Ф(Х, t ,т, и.)-ПФ*ЧЯ, t ,т)}х е!

х{Т*(Х, t ,т, ит)П^Х t ,т)}х j J                         , (1)

{S *(Х, t ,т, Us )-ПS (X, t ,т)} кеК где I, J, K – множество индексов компонент МТП, нанесенных на ИИ, элементы ОС и ПИ соответственно.

В большинстве случаев с достаточной степенью точности и независимо от физической природы процессов, происходящих в МОС, их абсолютные спектральные характеристики можно аппроксимировать разностными функциями вида

6(Хt,т,U ) = 6_t (t,т,и ) - 6Х - X(t , т )],

T (X, t ,т, U » ) = T (t ,т, и ) - TX - » (t , т )],     ₍₂₎

S (Х,t,т,US) = S. (t,т,US)-SX X (t)], где       фХ-Хф(t,т)],       т[X -Хт(t,т)],

S[X - X, ( t,т )] - относительные спектральные характеристики ИИ, ОС и ПИ соответственно; Ф_м ( t , τ , U_Ф ), T_м ( t , τ , U_Т ) , S_м ( t , τ , U _S ) – температурно-временные зависимости изменения максимумов их абсолютных спектральных характеристик; λ_ф ( t , τ ) , λ_T ( t , τ ) , λ_s ( t , τ ) – температурно-временные зависимости длин волн максимумов соответствующих спектральных характеристик. С учетом (2) спектральные характеристики элементов МОС имеют вид T ^*( λ , t , τ , U_T ),

6 (Xt,т,U 6 , U n6 , U » ) = 6 . ( t , т , U 6 ) - 6 [ Х - Х ( t , т )] х х Г Р Х, т , U 6 ) - 6, [ Х - Х„^1 , т , U „ 6 )];

/ е !

т* (Х, t ,т, U t , U nT , U n»» ) = т (t , т , U t ) - ЦХ - Х т (t ,т )] х х П с ?, ( / , т , U jT ) - с»!Х - ХТЛ< , т , U j» )];

, e J

5(Х, t , U_s , U S , U „S ) = S ( t , т , U s ) - 5 [ Х - X, (t )] х

HV. (t ,т, Us )-Sk [Х-й(1 ,т, U;,S)], kEK где UniФ,UnjT,UnkS – управляющие воздействия на максимумы пропускания соответствующих МТП, UniλФ,UnjλT,UnkλS – управляющие воздействия на сдвиг спектральных характеристик МТП.

Так как в общем случае для МОС наблюдается координатная зависимость спектральных характеристик по поверхности элементов, то их абсолютные спектральные характеристики запишутся в виде:

Ф * x. x, y , z , Х , t ,т, и ф *) = Ф *( Х , t ,т, Ц ф , и Пф , U / х ф ) - G_ф ( x , y , z );

T **( x , y , z , X , t,т,иф) = T *( Х , t,т, U t , U nT , U^ ) - G_T ( x , y , z );

S w( x, y, z, X, t ,т, US) = S *(X, t, Us , Uns, Unxs) -GS(x, y, z), где Gф(x,y,z), GT(x,y,z), GS (x, y,z)– весовые функции, учитывающие координатную зависимость соответствующих спектральных характеристик ИИ, ОС, ПИ соответственно, а UФ**,UТ**,US** – множество управляющих воздействий элементы МОС. Тогда с учетом выражения для освещенности [2] чувствительной площадки PП ПИ от смещенного относительно него на величину x0, y0 ИИ с излучающей площадкой PИ, получим обобщенное выражение для величины выходного сигнала ПИ в виде:

J ( t ,тЦ_ь,и т U s Ц ф , U T U k UU n x T U n x s ) =

ВЬ rrlf ^ф *^{г (} x >, У о , ^z o ^{, X} , ^t,т,UФ')■ T* ^{( x},y , ^{z , X} , ^t,т,UТ^ J ^J J z 2 JJ         [( x - x o )² + ( y - y o )² + z 2 ]         .⁽⁾

S" ( x, y , z , X , t , ^,^ ^)- d^ o dy o dxdy } dX

Выражение (3) позволяет учесть как вли- яние информационных и управляющих воздействий на элементы МОС, так и влияние внешних дестабилизирующих факторов (ВДФ).

В табл. 1 с позиций теории чувствительности приведены выражения для определения чувствительность МОС α_I = Δ J / J к изменению управляющих сигналов и ВДФ.

В таблице приняты следующие условные обозначения:

α jτ ₌       1       ∂ λ T^jn ( t , τ , U nⁱλT )

^{λ Tn} λ T^jn ( t , τ , U nⁱλT )       ∂ τ ,

kτ 1 ∂ λ ^kSn ( t , τ , U nⁱλS )

α λSn = _λ k _{Sn ( t , τ , Un} i _{λ S ) ∂ τ} – инерционность изменения длин волн максимумов спектральных характеристик МТП соответственно ИИ,

ОС, ПИ;

1   ∂ λ Ф ( t , τ ) α t ₌    1   ∂ λ T ( t , τ )

λ _Ф ( t , τ )   ∂ t , ^{λ T} λ _T ( t , τ )   ∂ t

α τ ₌     1     ∂ Ф м ( t , τ , U Ф )

^ФМ Ф м ( t , τ , U Ф )      ∂ τ     ;

1   ∂ λ S ( t , τ )

α τ ₌      1      ∂ S м ( t , τ , U S )

^SМ S м ( t , τ , U S )      ∂ τ ;

λS λ(t τ) ∂t    температурные коэф фициенты иS з,менения длин волн максимумов

–

спектральных характеристик ИИ, ОС, ПИ;

τ ₌      1      ∂ T м ( t , τ , U T )

^TМ   T м ( t , τ , U T )      ∂ τ

– инерционность ИИ,

1      ∂ λ ⁱфп ( t , τ , U nⁱ λ Ф )

λ ⁱфп ( t , τ , U nⁱ λ Ф )      ∂ t

ОС, ПИ;

α i τ ₌        1        ∂ Ф мⁱn ( t , τ , U Ф ) α k τ ₌       1       ∂ S м^kn ( t , τ , U T )

^ФМn Ф мⁱn ( t , τ , U Ф )       ∂ τ , ^SMn S м^kn ( t , τ , U T )       ∂ τ ,

α j τ ₌      1      ∂ T м^jn ( t , τ , U T )

^TMn T ^j ( t τ U )    ∂ _τ ^T – инерционность ИИ,

T_мn ( t , τ , U_T )      ∂ τ

ОС, ПИ по цепи управления МТП;

α ФМ =

1      ∂ Ф_м ( t , τ , U_Ф )

Ф_м ( t , τ , U_Ф )      ∂ t

α t  ₌      1      ∂ T м ( t , τ , U T )

^TМ    T м ( t , τ , U T )       ∂ t

α jt ₌       1      ∂ λ T^jn ( t , τ , U nⁱ λ T )

λTn λTjn(t,τ,UniλT)       ∂t       , kt          1      ∂λkSn(t,τ,UniλS)

α λ Sn = _λ k_{Sn ( t , τ , U n}i _{λ S ) ∂ t} – температурные коэффициенты изменения длин волн максимумов спектральных характеристик МТП соответственно ИИ, ОС, ПИ;

1      ∂ S_м ( t , τ , U_S )

– температурная чувстви-Sм(t,τ, US )     ∂t тельность ИИ, ОС, ПИ;

α it ₌       1       ∂ Ф мⁱ n ( t , τ , U Ф ) α jt =       1      ∂ T м^jn ( t , τ , U T )

^ФМn Ф мⁱ n ( t , τ , U Ф )       ∂ t      , ^TМ T м^jn ( t , τ , U T )       ∂ t      ,

β ₌ ∂ Ф [ λ - λ Ф ] , β ₌ ∂ T [ λ - λ T ]

∂ S [ λ - λ S ] β λ S =

∂ λ _S

– крутизна спектральной

характеристики ИИ, ОС, ПИ;

α kt ₌      1      ∂ S м^kn ( t , τ , U T )

^SМ   S м^kn ( t , τ , U T )      ∂ t

– температурная чув-

ствительность ИИ, ОС, ПИ по цепи МТП;

i ∂Фni[λ-λiФn] j ∂Tnj[λ-λTjn] k ∂Snk[λ-λkSn] βλФn =    ∂λiФn , βλTn =    ∂λTjn , βλS =   ∂λkSn - крутизна спектральной характеристики МТП

соответственно ИИ, ОС, ПИ;

α τ ₌    1   ∂ λ Ф ( t , τ ) α τ ₌    1   ∂ λ T ( t , τ )

^{λ Ф} λ _Ф ( t , τ ) ∂ τ , ^{λ T} λ _T ( t , τ ) ∂ τ ,

UФ α ФМ =

1     ∂ Ф М ( t , τ , U Ф )

Ф М ( t , τ , U Ф )    ∂ U Ф

τ 1   ∂ λ S ( t , τ )

^αλ S ⁼ _{λ ( t , τ ) ∂ τ} – инерционность изменения длин волн максимумов спектральных характеристик ИИ, ОС, ПИ;

A ^* = Ф [ λ - λ ф ( t , τ )] ⋅ ∏ Ф пⁱ [ λ - λ ⁱфп ( t , τ , U nⁱλФ )] ⋅ T [ λ - λ T ( t , τ )] ⋅

∏ Т п^j [ λ - λ T^jп ( t , τ , U n^jλТ )] ⋅ S [ λ - λ s ( t )] ⋅ ∏ S п^k [ λ - λ ^ksп ( t , τ , U n^kλS )] d λ

UT ₌      1     ∂ T М ( t , τ , U T )

^TМ T М ( t , τ , U T )    ∂ U T ,

US 1 ∂ S М ( t , τ , U S )

^α SМ ⁼ _{S М ( t , τ , U S ) ∂ U S} – чувствительность максимумов спектральных характеристик ИИ, ОС, ПИ к соответствующим управляющим воздействиям;

i ∈ J

λ _В

A = ∫ A 1 d λ _; α_λ ^{i τ} _Фn =

λ _Н

k ∈ K

1      ∂ λ ⁱФn ( t , τ , U nⁱ λ Ф )

λ ⁱФn ( t , τ , U nⁱ λ Ф )      ∂ τ

,

α iUФ ₌       1      ∂ Ф Мⁱ n ( t , τ , U Фⁱ n )

^ФМn Ф Мn ( t , τ , U Фⁱ n )    ∂ U Фⁱ n

α jUT ₌       1      ∂ T М^jn ( t , τ , U T^jn )

^TММ T Мn ( t , τ , U T^jn )    ∂ U T^jn     ,

,

Таблица 1 . Чувствительность МОС к управляющим воздействиям и ВДФ

Воздействие	Коэффициент чувствительности
Время A r	1 λ В «ФМ + a SM + ° TM + V ^Ф Мп. + ^ P Tm. + ^ a SMn + ^. J A [ Л ф>в?.ф а ю + " s e >S a >S + " т в т а ?т + i          j         k         A λ Н + Е " Фп в лФ. о 1Фп + Е " Тп в "тп а Тп + E^ kn e l O Sn ] d " i e l                  j e J                 k e K
Температура A t	1 λ В а ФМ + a-SM + ° TM + У а Ф>Мп. + V. QTmm + V a SMM +   J A [ " фгк^фф р- фф + S-s P kC Sm + TrPa*^?! + i          j         k         A λ Н + V Ффп Рш> а ^ФфФ п + V" тп в СТпаСТп + V кщпРпааЮ п ] d " i e I                  j e J                 k e K
Интенсивность излучения ИИ А ф , A U n^,	а фФ A и ф + V а ФМ A U^
Пропускание ОС AU t , A U nT	a TM A U T + V a TMT A UnT
Чувствительность ПИ A U S , A U S	афМ A U S + V akMn A uks k
Сдвиг спектральной характеристики МТП ИИ A UL	-1- J A 1 [ V " Ф. в 1ф.« Ф„ A ФФф ] d X A Н„   e I
Сдвиг спектральной характеристики МТП ОС A U "	4" 1 A ^ " Tn в La ф a UL ] d X A " Н    j e J
Сдвиг спектральной характеристики МТП ПИ A U "	4- J A 1 [ V " ksn в ksn a A uLs ] d x A        k e K

1      <,(t ,T, U )

S m, (t,T,u )    U,     - "чувств^11-

тельность максимумов спектральных характеристик МТП соответственно ИИ, ОС, ПИ к соответствующим управляющим воздействиям;

_a iu =      1     ay t ,Т, i )

' Ф((tT,фф)5^ ’ аи =   1   X (t TUT )

Tn T. (t TUX)   d’ a =   1   X (ttUs )

Sn"   XS.(t чувстви-

тельность изменения длин волн максимумов спектральных характеристик МТП соответственно ИИ, ОС, ПИ к соответствующим управляющим воздействиям.

Как видно из (3) и табл. 1 выходной сигнал ПИ определяется величиной излучаемого ИИ светового потока, спектральными характеристиками МОЭ и взаимодействием этих спектральных характеристик. Причем, этим взаимодействием можно управлять как путем изменения соответствующих управляющих воздействий, так и изменением крутизны и взаимного расположения спектральных характеристик элементов. Указанные свойства оптических фильтров позволяют создавать различные типы сенсоров с высокими метрологическими и эксплуатационными показателями.

ОПП с интерполяцией периода шкалы

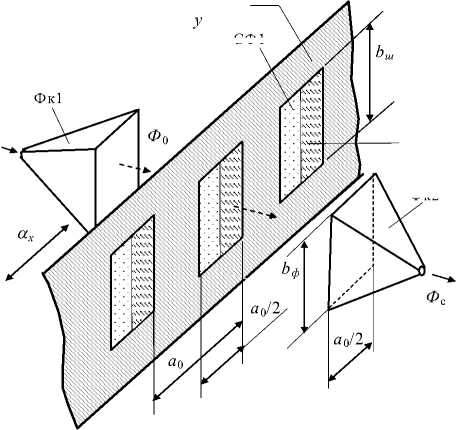
На рис. 2 показана упрощенная структурная схема оптомеханичекого сенсора двухотсчетного цифрового ОПП, в котором модулирующая шкала выполнена из окон прозрачности шириной а ₀ /2, где а ₀ – период следования окон. Каждое окно представляет собой конструкцию из двух светофильтров (СФ1 и СФ2) с длиной волны l ₁ и l ₂ и полосами пропускания Dl ₁ и Dl ₂ соответственно.

Пространственно-спектральное разделение окна предназначено для определения направления перемещения шкалы и устранения неоднозначности кода перемещения в пределах периода а ₀. Световой поток Ф ₀ в диапа-

Шкала

СФ2

Фк2

СФ1

окна на выходе фоклина Фк2, выполняющего функции считывающего элемента (СчЭ), формируется оптический сигнал

О, = О 0 [ Ё„Т ( Я ) + Ё„Т ( Я ) ] , где t ₁( l ), t ₂( l ) – спектральные характеристики пропускания СФ1 и СФ2 соответственно; Ê _{1 α} , Ê _{2 α} – функции модуляции светового потока, определяемые текущим значением перемещения a и чертежами CФ.

Если граница раздела СФ проводится через центр окна параллельно боковым границам (см. рис. 2,а), а геометрические размеры широких торцов Фк1 и Фк2 идентичны ( а_й = а, = а 0 /2), то

а)

αα

—, 0 <  а < —

α ₀

αα

— <  а < —

б)

Рис. 2. Структурная схема (а) и эпюры сигналов (б) цифрового ОПП с модулирующими светофильтрами

^K 1 α

K 2 а =^

2,

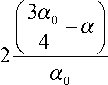
α     3 α

— <  а <  —⁰ ;

0,

3 α

⁰ <  а < а,

0, 0 <  а < ^0-

α а —0

αα

---—, —⁰ <  а <  —⁰

α0     42

• 1    α3

• —, —⁰ <  а <  —⁰

( а ^{- а} ) 3 а

2- -----⁰, —⁰ <  а < а

α0      4

зоне А Я е А Я 1 , А Я 2 от источника излучения (ИИ) через оптическое волокно (ОВ) направляется на фоклин Фк1, выполняющий функцию диафрагмы, в котором формируется об-

лучающее световое пятно площадью S 0 = a 0 Ъ₆ /2 >  a 0 b₀ /2, где Ьф - высота широкого торца фоклина, b_ш – высота окон шкалы ( b_ф і b_ш).

В процессе перемещения шкалы в пределах [ iа₀, ( i + 1 ) а ₀ ] , где i =1, 2, „.- номер

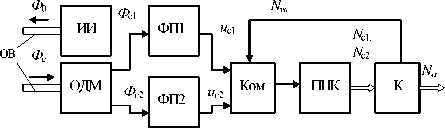
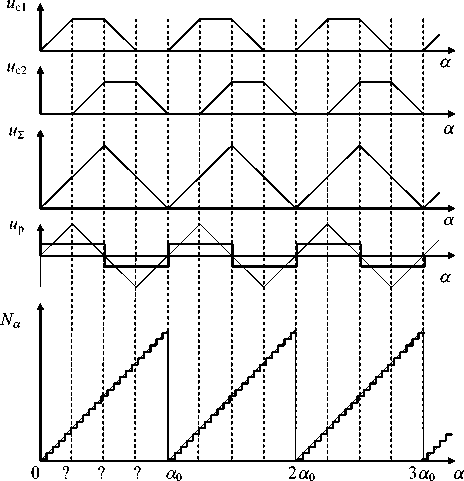
С выхода оптического демультиплексора (ОДМ) на фотоприемники ФП1 и ФП2 подаются два оптических сигнала Ф_с 1 и Ф_с 2, Выходы ФП через коммутатор (Ком) подключены к преобразователю напряжения в код (ПНК), соединенного с информационным входом контроллера (К). Алгоритм работы контроллера иллюстрируется эпюрами сигналов (рис. 1,б), из которых видно, что из суммарного сигнала u_S формируется неоднозначный код перемещения, а из разностного u_p – код определения направления перемещения.

Недостатком таких преобразователей

( i +2) α 0

( i +1) α 0

α

а)

A U₂ /U₃

б)

U ш

° I I I I k| I | I । k| I |

в) ЛК1

a

ЛК2 г)

ЛК3 д)

zl___La

| a" '   *a

Рис. 3. ОПП с высоким отношением Uc/Uш: а) - структурная схема; (б-д) - эпюры сигналов является низкая точность преобразования вследствие уменьшения отношения сигнал/ шум в точках, кратных а 0 + а 0/ NTO max, где NTOmax = 2"TO — максимальное значение интерполирующего кода точного отсчета.

Вариант шкалы с высоким отношением U_c/U_ш в интерполируемых квантах показан на рис. 3. Каждый квант периодом a ₀ состоит из трех СФ, шириной α_o /2 и смещенных на величину α_o /3.

Выходы ОДМ через соответствующие фотоприемники ФП1 – ФП3 подключены к трем подключенным к контроллеру логическим компараторам (ЛК1-ЛК3) и управляемый коммутатор. На вход ЛК1 поступают сигналы с ФП1 и ФП2 ( и , и и 2 ) , на вход ЛК2 — с ФП2 и ФП3 ( и 2 и и 3 ) , на вход ЛК3 - с ФПЗи ФП1 ( и и и з ) . Код управления, формируемый из выходных сигналов ЛК, определяет

Таблица 2. Алгоритм работы схемы выбора линейных участков

№ комб. Соотношения вых. сигналов ЛК Сост. вых. ЛК Сигн. на вх. ПНК 1 2 3 1 u2>u1, u3>u1 0 0 1 u2 2 u2>u3, u1>u3 0 1 0 u1 3 u2>u3, u3>u1 0 1 1 u3 4 u2u2 1 0 0 u3 5 u2u1 1 0 1 u1 6 u2>u3, u1>u2 1 1 0 u2 порядок прохождения сигналов с ФП1-ФП3 на вход ПНК.

В табл. 2 показан алгоритм работы логической схемы ОПП, позволяющий получить на входе ПНК сигнал треугольной формы с периодом a_o /3, свободный от плоских и зашумленных участков (рис. 3,б). Сущность логического управления заключается в инвертировании знака приращения при переходе с линейно возрастающего на линейно спадающий участок сигнала и ( x ) (рис.3,в-д). В результате на выходе контроллера формируется код, пропорциональный перемещению во всем диапазоне преобразования.

Информационная емкость и быстродействие преобразователя определяются параметрами реверсивного счетчика. Современные счетчики позволяют находиться в рамках заданной динамической погрешности при информационной емкости n =16 бит, диапазоне перемещения L =100 мм и скорости перемещения da/dt= 15…50 м/с. Полная автокоррекция погрешности разметки шкалы при этом будет обеспечена до величины

| ^A a 1,2max

a o

। " 6 .

Если чувствительность ПНК

,

I U o I

" пнк = ^log 2 1 TT7   I = ⁸ , то количество

^{VA U} МР )

квантов равно n = 2 n - 2 n ПНК = 256. Допус— тимая погрешность разметки A a 1 _2max = 65 мкм.

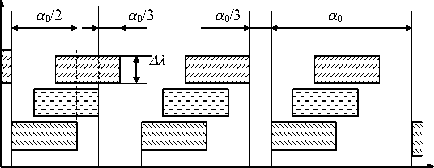
С целью повышения энергетических параметров интерполяционных сигналов, определяемых шириной спектра, применяется нониусная шкала из широкополосных СФ (ШСФ) с высокой точностью нанесения границ. На рис. 4 показан чертеж фрагмента шкалы, которая выполнена из периодически нанесенных групп из N =8 ШСФ с взаимно смещенными на вел ич ину ( j- 1) Dl_н полосами пропускания ( j = 1, N ). Ширина каждого фильтра равна ширине СчЭ а₆ = а_Й = а ₀ / 2 . Фильтры смещены вдоль шкалы на величину Da = a ₀/ N. Перемещение шкалы на величину jDa приводит к изменению спектра суммарного сигнала на входе ОДМ, соответствующему одной из М =11 комбинаций, представленных в табл. 3.

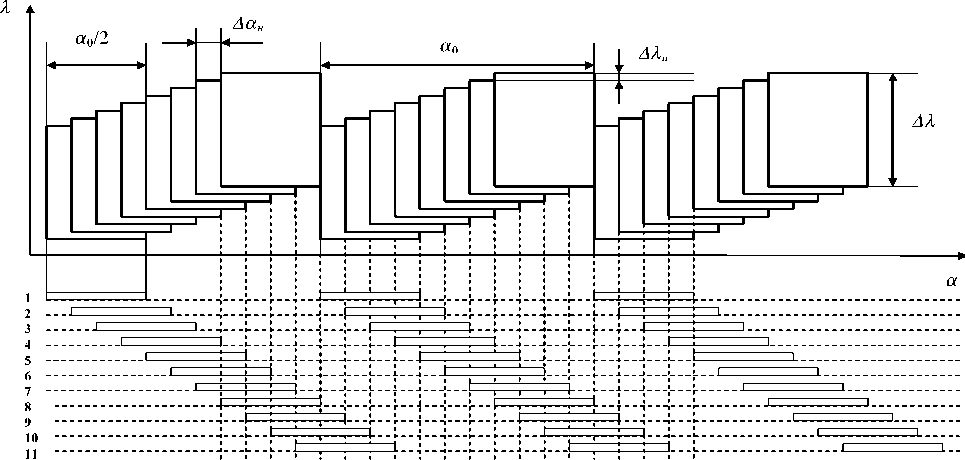
Рис. 4. Формирование рисунка кодовой шкалы из N =8 светофильтров на периоде a ₀

Достоинством такого алгоритма является однозначность интерполяционного единичного позиционного кода (ЕПК).

Для преобразования выходных ЕПК в двоичный код более удобно формировать число градаций м = 2 n et путем изменения числа N и уплотнения межгруппового расстояния на величину kDa_н . При этом необходимо выполнение условия сохранения минимума энергии сигнала

В ряде работ предложены различные эффективные чертежи шкал с применением светофильтров и схем расстановки СчЭ со спектроформирующими покрытиями, в которых корректируются погрешности, связанные с переходом между 0 и N _max, перекосом линии считывания, дифракцией и рассеянием светового потока [1-3, 6-9].

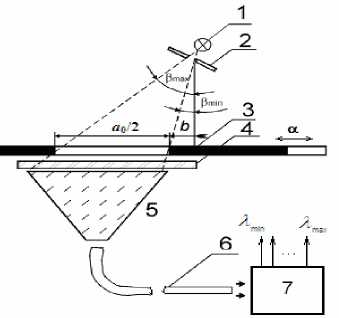
Структурная схема ОПП со спектрально-модовым кодированием перемещения представлена на рис. 5 [6]. При установке СФ 4 за шкалой 3 параллельно ее поверхности лучи от осветителя 1, проходящие через диафрагму 2, попадают на поверхность СФ 4 расходящимся пучком, который воспринимается фоклином 5. Часть лучей угловой апертуры пучка заключается в диапазоне углов Db=bmax-bmin, границы которых, для согласования с ОДМ определяются в соответствии с выражениями в mах = arccos —ma max

λ ₀

^в mm = arccos

λ min λ 0

2 d

= arctg----- a 0 + b

2 d

= arctg—

где l _max , l _min – максимальная и минимальная длины волн рабочего диапазона ОДМ; d – расстояние между плоскостью отверстия диафрагмы 2 и поверхностью КШ 3 со стороны

Таблица 3. Формирование ЕПК

№ поз. (ЕПК)	Номера центральных длин волн засвеченных СФ
1	1	2	3	4
2	2	3	4	5
3	3	4	5	6
4	4	5	6	7
5	5	6	7	8
6	6	7	8	-
7	7	8	-	-
8	8	-	-	-
9	8	1	-	-
10	8	1	2
11	8	1	2	3

Pис. 5. Структурная схема сенсора ОПП со спектральным кодированием перемещения

УИС 4; a₀ – период КШ 3; b – расстояние от нормали, восстановленной из отверстия диафрагмы к поверхности УИС 4 до участка УИС 4, пропускающего излучение с длиной волны l _min.

Согла^. сование производится варьированием l _max, l _min, d, b . с учетом фазового поперечного сдвига Dx падающего светового луча (рис. 5, 6), ограниченного диапазоном А в = в max - e min .

Световой луч точечного источника описывается уравнением падающей волны

A ( r ) = A 0 exp

—

r

R

где r²=u²+v² ; u , v , w – приведенные декартовы координаты.

На основании анализа Фурье такой луч можно представить в виде суммы плоских волн +^

A ⁽ r ) = J J A ( k u , k v ) e ^— ikr dkudkv , (4) где | k |² = k ² + k v + k W ; k u , k_v , k w ^- компоненты волнового вектора в декартовой системе координат.

Компоненты k_u и k_w плоской волны, движущейся под углом Db к направлению падения луча, связаны между собой соотношением А в = k u / k w .

Фаза отраженной компоненты плоской волны, для которой ku << kw, сдвигается на величину d^(^R

^T А в ^T 0 ⁺ dp ( ^{А в} max ) -

Отсюда с учетом (4) следует, что отраженный луч сдвинут в поперечном направ-

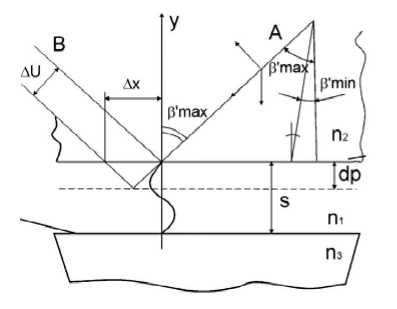
Рис. 6. Формирование поперечного фазового сдвига светового луча л 1 dT лении на величину Au =-- kϖ ∂βmax

Глубина проникновения световой волны из среды с показателем преломления n ₁ ^o в среду с показателем преломления n ₂ ^o равна

, cos 1   dT dp = max-—--, 2tgβmax n1k0∂βmax

а фазовый сдвиг

^AT = 2 dptg^ max .         ⁽⁶⁾

Производная фазы светового луча по параметру максимального значения угла падения светового луча равна где

d T =	(    k 2 u 1	∂
дв т., =	2 +^-2 V ku 1 + ku 2 У	дВ max

(4 )

V ^ku i У

* £= ( " ° ) ² k 0 ² ( 1 — sin² в max ) • (8) k u = ^k 02 ⁽ ( " ° ) ² S ⁱⁿ 2 A max ^— ( " о ) ² ) . (9)

,

Подставляя выражения (8) и (9) в (7) и (6), получим

^AT k t^ mx - (10) u ₂

Из (10) следует, что для согласования фазовых фронтов волн во всех точках вдоль границы раздела сред необходимо варьировать значениями b_min и b_max . Световой пучок испытывает полное отражение от поверхности раздела _n 2° - _n ° , что приводит к установлению моды стоячей волны в интерференционном светофильтре. Эта мода является стационарной в направлении оси у , но движется в направлении оси x с фазовой постоянной k_m. В фоклине может существовать несколько мод с фазовыми постоянными ( k_m = 1,2,3 ... ). Эти моды имеют экспоненциально убывающие “хвосты”, частично заходящие на поверхность раздела " ° _{— n} 3° . Зазор S между фок-лином и СФ выбирается в районе 100 нм из расчета перекрытия “хвостов” мод фоклина, с учетом согласования фазовых фронтов волн DY таким образом, чтобы k = k m , что удовлетворяет условию когерентной перекачки сдвинут в поперечном направлении на энергии моды СФ в моду m -ro порядка фоклина. Позиционный спектр мод передается фоклином через волоконно-оптическую линию связи в ОДМ.

Если приравнять число мод, возбуждаемых в фоклине в пределах a₀/2 , к числу N , то шаг Dа интерполяции определяется выражением

α d λ cos β ka =----0, 1 0    -—

• ⁴ d 2 V( n 1 ) - ( n 3 ) ,

  
  

где d ₁, d ₂ - ширина входного и выходного торцов фоклина соответственно;

d 2      о ² о ²

d " v ( n i ) - ( n з ) — числовая апертура фоклина.

ОПП абсолютного считывания с однодорожечной цифровой шкалой

Применение структурированной по цифровому закону комбинации из светофильтров

Шкала

ИИ

КСФ

Ф с

Т ( X )

IV т (X)

III

Ж

λ

Я'

Т ( X )

ШЩ

Т ( X )

IWUL

б)

λ

λ

II

I

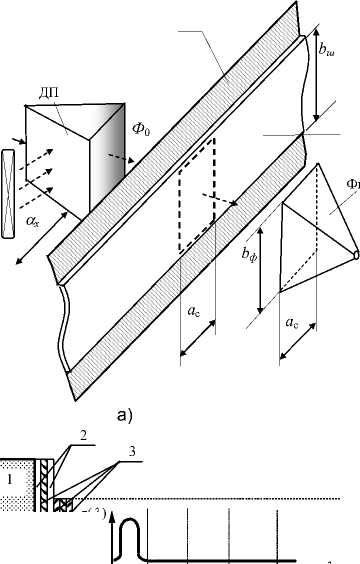
Рис. 7. ОПП с ЦШ на комбинированном узкополосном светофильтре: а – структурная схемам; б – принцип нанесения комбинированного светофильтра позволяет значительно сократить величину рабочей зоны bш цифровой шкалы ЦШ (рис. 7, а).

Световой поток от источника излучения ИИ проходит через дисперсионную призму ДП, шкалу с нанесенным на нее комбинированным светофильтром КСФ и фоклин Фк, сопряженный со световодом - к ОДМ в составе электронного блока. КСФ (рис. 6,б) представляет собой многорезонансную узкополосную интерференционную систему, состоящую из нанесенных на прозрачное основание 1 зеркальных четвертьволновых 2 и резонансной полуволновой 3 пленок, формирующих опорный слой кодовой дорожки. Порядок интерференции m выбирается так, чтобы в полосе чувствительности СчЭ укладывалось число n полос прозрачности интерференционной системы, соответствующее числу разрядов выбранного кода преобразования. На участки 1, 2, 3,.2 ⁱ ,...,2 ⁿ кодовой дорожки с периодом a_i = Q /2 ⁱ наносятся дополнительные четвертьволновые зеркальные составляющие 2 шириной a_i/2 .

Эти составляющие вырезают из основных полос пропускания l _m1, l _m2,..., l _{m n} соответствующие каждой разрядной дорожке полосы Dl _m1, Dl _m2,..., Dl _{m n} . Такое расположение зеркальных составляющих позволяет осуществить спектральное кодирование светового потока, связанное с перемещением a_х ЦШ. Например, для трехразрядного цифрового ОПП в полосе чувствительности ОДМ должны находиться три полосы пропускания интерференционной системы: основная Dl _m1 и две дополнительные Dl _m2 и Dl _m3( на рис.6,б участки I-IV). На опорный слой кодовой дорожки с указанными полосами пропускания наносятся три дополнительных заграждающих четвертьволновых слоя. Первый слой, не пропускающий излучение с длиной волны l _m1 , наносится с периодом а ₁. На него с периодом а ₂=2 а ₁ наносится слой, не пропускающий излучение с длиной волны l _m2 , и далее сверху с периодом а ₃=4 а ₁ наносится слой, не пропускающий излучение с длиной волны l _m3 .

Соответствие между выходным кодом датчика и параметрами интерференционной системы приведено в табл. 4.

Последовательное нанесение УИС друг на друга в геометрических пределах одной дорожки ЦШ позволяет достичь n -кратного

Таблица 4. Формирование кодовых комбинаций

Номера разрядов выходного кода			Наличие	заграждающих		Спектральный состав излучения на
перемещения			четвертьволновых систем			выходе КШ
1	2	3	λ m1	λ m2	λ m3	λ m1	λ m2	λ m3
0	0	0	-	-	-	+	+	+
0	0	1	+	-	-	-	+	+
0	1	0	-	+	-	+	-	+
0	1	1	+	+	-	-	-	+
1	0	0	-	-	+	+	+	-
1	0	1	+	-	+	-	+	-
1	1	0	-	+	+	+	-	-
1	1	1	+	+	+	-	-	-

сокращения рабочей зоны b _y . Допустимая величина радиального перекоса ЦШ при b _y=20 мм, а ₁=0,184 мм равна D j _1max=1,05^о, а при b _y =1 мм D j _1max=15,05^о. Вся информация из сенсора передается в ЭБ по единственному световоду без перекрестных помех между разрядными каналами.

Заключение

Спектральное кодирование перемещения с помощью спектроформирующих элементов (СФЭ) значительно снижает требования к точности расположения СчЭ относительно шкалы. В результате снижаются трудозатраты на изготовление сенсоров и упрощается конструкция кодирующих узлов. Погрешность преобразования определяется подбором СФЭ, рабочая длина волны которых может выдерживаться с точностью до нанометра. Создается возможность для применения различных методов мультиплексирования информационных каналов, существенно сокращающих количество волоконно-оптических линий связи.