Спектральные преобразования в приспособленном базисе для разделения "наложившихся" пиков и фильтрации масс-спектрометрических сигналов

ВВЕДЕНИЕ                   ний с параметрически перестраиваемыми по фор-

Во многих научно-технических областях, в которых применяются масс-спектрометрические приборы, в основе решения прикладных задач лежит обработка сигналов, поскольку через их анализ как носителей информации раскрывается информативное содержание, связанное с решаемой задачей. Получение достоверной информации из масс-спектрометрических сигналов в ряде случаев осложняется недостаточным разрешением приборов и наличием нежелательных шумов и наводок. Применение в программном обеспечении масс-спектрометров алгоритмов, позволяющих снизить их влияние, является актуальным в настоящее время. Во многих практических задачах, связанных с обработкой сигналов, нашли применение ортогональные преобразования, и в частности те из них, которые имеют быстрый вычислительный алгоритм, обеспечивающий возможность оперативного анализа данных. В этой области в последнее время активно развиваются параметрически перестраиваемые ортогональные преобразования с быстрыми алгоритмами, предложенные в работах [1–8], которые позволяют изменением параметров приспосабливать оператор преобразования к характеру исходных данных. Настоящая работа посвящена решению задачи разделения и фильтрации масс-спектрометрических сигналов. В процедурах обработки сигналов предлагается применить аппарат ортогональных преобразова-

ме базисными функциями, что создает возможность приспосабливать такое преобразование к анализируемым данным. Целью данной работы являются разработка, теоретическое и экспериментальное исследование алгоритмов разделения и фильтрации масс-спектрометрических сигналов, обеспечивающих повышение достоверности их оценивания.

ВЫБОР МАТЕМАТИЧЕСКОЙ ОСНОВЫ ДЛЯ РАЗРАБОТКИ АЛГОРИТМА

Предварительные замечания

В данной работе рассмотрен метод анализа сигналов, представленных в дискретной форме, что соответственно относится и к представлению ортогональных преобразований. В основе метода лежит быстрый алгоритм преобразования. Возможность приспособления к обрабатываемым данным базисных функций используется для существенного сокращения размерности их представления в спектральной области, в которой сохраняется исходная информативность данных, благодаря чему можно не только упрощать вычисления в процедуре анализа, но и существенно повышать достоверность ее результата.

Задача по выявлению информативных признаков в масс-спектрометрических сигналах может быть представлена как задача нахождения вектораY

Y = FX, где X = [x1,x2,...,xN]T— вектор исходных данных преобразования; Т — означает транспонирование матрицы или вектора; F — оператор преобразования; Y = [y1,y2,...]T — вектор признаков, который должен адекватно характеризовать вектор исходного описания с точки зрения задачи оценки параметров масс-спектрометрического пика, а размерность пространства признаков могла бы быть существенно меньше размерности исходных данных. При решении этой задачи возникает вопрос выбора класса оператора преобразования F. Известно [9-13], что общий подход к отысканию процедур оценки признаков (параметров масс-спектрометрических сигналов) основан на линейных преобразованиях. Среди них наибольшее распространение получили ортогональные преобразования [14]. При использовании ортогональных преобразований имеется возможность выбора систем базисных функций, наиболее приспособленных к решаемой задаче. При этом может обеспечиваться высокая вычислительная эффективность таких преобразований, которые могут выполняться по быстрым алгоритмам.

Ортогональные преобразования, основные свойства

В рамках теории цифровой обработки сигналов понятие ортогонального преобразования может быть представлено в виде матричного уравнения

Y = HX, где Н — матрица ортогонального преобразования; X = [x1,x2,...,xN]T — вектор анализируемого сигнала; Y = [y1,y2,...,yN]T— вектор спектральных коэффициентов (является отображением Х в спектральной области).

Оператор преобразования Н включает в себя систему базисных функций и имеет структуру

H =

h h 2

hM

^[ h jj ""  h l N ^{] [} h 2j •" h 2 n ^]

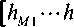
MN ^]

где [ h i ₁, h i ₂, — , h_iN ] — вектор дискретных значений i -й базисной функции.

Система функций { h i } является базисной, если все функции ортогональны друг другу, т. е. для любых 1 <  i <  N , 1 <  k <  N ( i ^ к )

N

Z h*, = °- j = 1

При этом образуют полную систему, для которой не существует ни одной другой функции, ортогональной ко всем остальным, что выполняется, если для любого 1 <  i <  M

N

Z h ij g j = ° ^ g j = °.

j = 1

При выполнении условия полноты имеет место равенство М = N .

Система ортогональных базисных функций является нормированной (или ортонормированной), если норма каждой базисной функции в пространстве L ₂ равна единице, т. е. для любого 1 <  i <  N

N

Z h ij ² = 1.

j = 1

В геометрической интерпретации результатом ортогонального преобразования исходного вектора являются его проекции на оси ортогональной координатной системы. Аналогами этих проекций при ортогональном преобразовании являются спектральные коэффициенты. Отсюда для спектральных коэффициентов вытекает важное свойство, которое выражается в их взаимной независимости. Для преобразований по системам орто-нормированных базисных функций справедливо равенство Парсеваля

N

N Z X- ’

M = Z у - ².

При этом исходный вектор Х и его спектр У информационно эквивалентны [4, 15]. Это свойство особенно важно для решаемой в работе задачи. Отмеченные свойства означают, что существует обратное преобразование, т. е. возможно восстановление исходного вектора из спектра У :

X = H*Y, где H*— комплексно-сопряженная матрица оператора в общем случае. Для вещественного базиса Н* = HT.

Выбор той или иной базисной системы производится по требованиям конкретной задачи анализа сигналов. При решении задачи оценки параметров "наложившихся" пиков базис должен обеспечивать получение пространства информативных признаков невысокой размерности и выражаться в факторизованной форме, которая ведет к возможности оперативного выполнения ортогонального преобразования по быстрому алгоритму. Сокращение размерности при этом заключается в том, что при ортогональном преобразовании основная информативная (релевантная) часть исходной информации концентрируется в k спектральных коэффициентах (k << N). За счет исключения остальных спектральных коэффициентов как неинформативных размерность вектора информативных признаков существенно уменьшается. Таким образом, следует выбирать ту базисную систему, которая обеспечивает максимальное уменьшение размерности вектора информативных признаков при минимальных информационных потерях. В работе [16] предложен новый подход к построению ортогональных преобразований с параметрически перестраиваемыми по форме базисными функциями с сохранением их ортогональности и полноты. Рассмотрим аппарат таких преобразований более подробно.

Перестраиваемые ортогональные преобразования

Существо метода перестраиваемых ортогональных преобразований состоит в таком факторизованном представлении матрицы спектрального оператора, в котором ненулевые элементы факторизованных матриц взаимосвязаны условиями ортонормированности и полноты и имеют степени свободы, обеспечивающие параметрическое формирование множества базисов с алгоритмами быстрых преобразований. В основе построения алгоритма лежит представление оператора преобразования H в виде произведения слабозаполненных (факторизованных) далее неразложимых матриц

H = G n G n - 1 - G_o              (1)

Gi(ф,1 ,-,ф N) — факторизованные (слабозапол-i ненные далее неразложимые) матрицы, ненулевые элементы которых зависят от параметров фlJ,

n ; j = 1, - ,

N

2 , где n — число факторизо- ванных матриц Gi, в частности при N = 2n, равно log2 N (N — размерность оператора H). При этом N каждая из матриц Gi содержит 2 элементарных матричных блоков, обобщенная модель которых имеет параметрическую форму и названа в силу неразложимости спектральным ядром. Для операторов размерности N = 2n факторизованные матрицы Gi составляются из параметрических элементов ядер v.. = ij

^a j ^- Y j

W - 5j

Пример структуры факторизованной матрицы G _i имеет вид

G =

Г а_п _ в

_ 0 =

0         0     Yn

0             0

ai2 00

^2 00

0   aN2

-  0  eN/

_ ¹ /2

Y 2 5

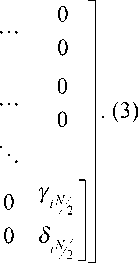
В этом случае параметрические элементы матриц-ядер (2) вычисляются следующим образом:

^j — ^         ¹ j

^J = В ... 5

_^j           ij

cosc ^ .j ^-    w_lJsⁱⁿ⁽ 9_{l J} )

sm( p,. j )    ^- - w ,, j cos( ^ ,. j )

W , j = exp( j 0 , j ), ф e [ 0,2 n ] , 6 e [ 0,2 n ] .

Задавая параметры элементов ядер ф , ₃ и 6 , _J , можно формировать спектральные операторы H с комплекснозначными и при 6 , j = 0 вещественными базисными функциями по условию решаемой задачи.

СИНТЕЗ ПРИСПОСОБЛЕННОГО БАЗИСА ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ

Как отмечено в предыдущем разделе, факторизованное представление матричного оператора H может быть использовано для синтеза произвольных систем дискретных функций путем задания элементов ядер. Конструктивная основа синтеза спектральных операторов в ортогональных базисах дана в работе [17], в которой получено аналитическое выражение обобщенного спектрального ядра для класса полных ортонормированных систем функций. В данной работе для решения поставленных задач использован один из предложенных в работе [8] вариантов синтеза приспособленного оператора. Систему приспособленных базисных функций, отвечающих требованиям ор-тонормированности и полноты, предлагается строить на основе заданного эталона R _эт . Оператор ортогонального преобразования полагаем приспособленным к R _эт , если выполняется условие

T

N H п R эт = Y₄ =_ У ц 1 ,0, ^ ,0 ] .        (4)

Здесь H _п — приспособленный оператор; Y _ц — целевой вектор, принимаемый в качестве критерия настройки оператора; R эт = ^{[ г}эт ,1 , _ , ^гэт , N J T — вектор обучающего эталона, который должен быть нормирован, т. е. удовлетворять условию

1N r2

N £ ^эт, ‘

= 1.

При соблюдении соотношения Парсеваля

NM

— У г² =У У². =1 эт , i           y ц , i

N i = 1             i = 1

Соотношение (4) удовлетворяется при определенных параметрах ф _ij факторизованных матриц G _i . В работе [8] определены правила вычисления этих параметров, обеспечивающих выполнение условия (4), и описана итерационная процедура построения приспособленного базиса. В соответствии с [8], покажем подход по проведению итерационной процедуры. Поясним его на примере векторов R ^ˆ _эт с размерностями N = 2 и N = 4.

Для случая N = 2 имеем:

целевой вектор также будет получен в нормированной форме Х ц = [ 1,0,...,0 ] ^Т.

В [4] изложен подход для настройки оператора H по заданному нормированному эталону R _эт класса анализируемых сигналов. Суть состоит в отыскании угловых параметров ф^ спектрального оператора H _п , удовлетворяющих условию (4). Число угловых параметров зависит от длины вектора анализируемого сигнала. В настоящей работе использован алгоритм, описанный в [8], в котором факторизованные матрицы оператора H _п принимаются одинаковой структуры.

Пусть вектор эталона R _эт имеет размерность N . Требуется найти параметры оператора H _п , удовлетворяющего условию (4). Как и в (1), представим H _п в факторизованном виде. При этом можно записать:

1       -                    1

N H п R эт = Х ц ^ N G n G n - 1 ...G = Y₄ ,

где n = log₂ N . Факторизованные матрицы G i

принимаем следующей структуры:

Gi =

Ci    0          0     Su      00

sn   0         0    - cn J    00

0   [Ci2   0             0     s^ ]

0    L Si2   0              0     - ci2 J

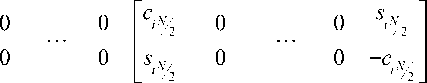
где     c j = cosC ^ j .);     s j = sinC ^ j .);     i = X.., n ;

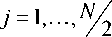
c ^{1 S 1}      r

. s l ^- c l JL r 2

c l где ^

s ₁

= cos( ^ l ), = sin( ^ l )-

У 1       I c l r l + s l ^r 2

. У 2 ^J I s l r l ^- c l ^r 2

y1, y2,

Необходимо обеспечить равенство Y _l = Х ц , что

выполняется при y 2 = s _l r - c_l r ₂ = 0, откуда получа-

ем:

S r           r

— = — ^ ф ₁ = arсtg — c l r i                     ( r i

Для случая N = 4 имеем:

G 2 G 1 R эт = Y .

Рассмотрим первый де^ния G 1 ^R эт = Y l :

шаг в процедуре произве-

где

c ₁₁    0 s ₁₁

s ll ^{0 -} c ll 0 c ₁₂ 0    s ₁₂

r ₁

r ₂

r ₃

12 JL r 4

У 11 = c ll r + ^S 21 ^r 3 , y 12 = s ll r l ^- c ll r 3 , y 13 = ^C 12 r 2 ^{- S} 12 r 4 , У 14 = ^S 12 r 2 ^{- C} 12 r 4 -

^y 11

^y 12

^y 13

y ₁₄

Обратим внимание на зависимость элементов Y ₁ . Можно видеть, что элементы y ₁₁ и y ₁₂ этого вектора определяются произведением первого ядра матрицы G ₁ на элементы r ₁ и r ₃ , и соответственно y ₁₃ и y ₁₄ находятся аналогично через произведение второго ядра на элементы r ₂ и r ₄ . Эту особенность можно отразить поядерной записью:

^c 11

^s 11

⁵ 11      r l

- cii JL r

^y 11

^y 12

^c 12

^s 12

c 12

r ₂

^y 13

^y 14

У - - 1,1

У . - 1,2

^yi ,1

^yi ,2

из которой вытекают выражения для вычисления двух искомых параметров:

Ф 11 = arctg -1- l r

Ф 12 = arctg    2

l r 4

что приводит вектор Y1 к виду yi,N

Y 1 = [ ^ ,„0, У .0 ] .

По аналогии для второго шага произведения

G ₂ Y 1 = Y ₂ имеем:

c 21

0

s 21

0

[ У Ч

[

y 21

1

5 21

0

c 21

0

J J

0

J —

y 22

J J

0

c 12

s12

У 13

y 23

,

_ 0

s 12

c 12 ]

_ 0 ]

J

_

y 24

J

c 21     5 21

" У 11 "

=

[ У 21 "

c 21     5

21

1

" 0 "

=

" У 21 "

_ 5 21

c 21 ]

_ y 13 ]

_ У 22 ]

,

_ 5 21    -

c 21

_ 0 ]

_ У 22 ]

Откуда находим параметры

(здесь • — знак умножения матрицы на вектор).

По аналогии с рассмотренным выше можно записать:

ci 1	5 1	"  У. - 1,1   "	= [ У - ,1 "
_ 5i 1	- c . 1 ]	yN i - 1,1 +--	L у . ,2 ]
		_          2 ]

c . 2	5.2	У. - 1,2		"У. ,3"
_ 5. 2	- ci 2 ]	yN i - 1,2 +— _          2 ]		_ У . ,4 ]

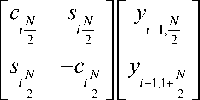
Ун Ф 21 = arctg       ,

. ^y 13 ,

^ф 22    ⁰ ,

Требуемый результат на i -й итерации

при которых достигается искомое равенство

Y 2 = Y = [ y 21 ,0,0,0 ] T .

Y , =[ y ,N -Л - ,0 ] T

^

c_N 2

s_N 2

y_N i "Ч

Рассмотрим случай отыскания параметров ф _ij для произвольной размерности N = 2 n факторизованного оператора H = G n G n - 1 ^ G 1 .

В процедуре вычисления ф^ выделим промежуточную итерацию G,Y i - 1 = Y i :

ci 1	0	0
si 1	0     ’"	0
0	" с .2    0
0	_ 5.2    0
0	0	" cN/ 1 /2
0	’"     0	5/N/ L i / 2

- Ci1J

^{0 s}i 2

⁰      - c i 2

0’"

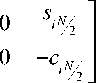
s_N 2

- c N

yN i-1,1+--

обеспечивается при

Ф n = arctg i

Ф.^ = 0

Можно

n ,

y_N i - 1, ₂

i - 1,1 +— 2

,

y i , N - 1

если У N = У N = 0. I - 1,—         i - 1, + 1

утверждать,   что для любого

N

, , 2

cs cij s-c ij ij

выполняется при

требуемый результат

y i ,2 j - 1 0

j ^arctg

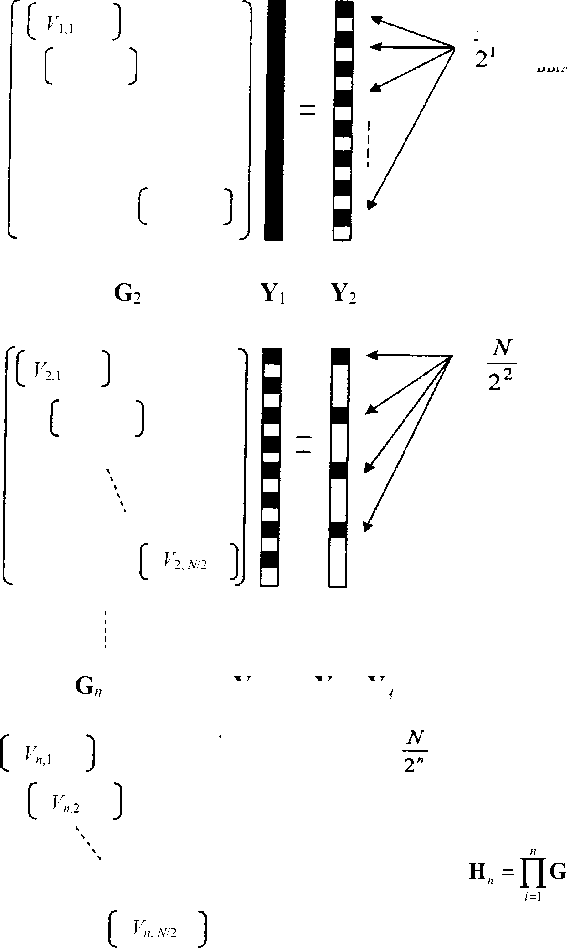
Рассмотренные итерационные процедуры можно пояснить схемой, показанной на рис. 1, где длина черной полоски обозначает число ненулевых элементов вектора.

ф у = 0, если у „ = у, -1 . = 0. " I, j +

Первая

итерация

Вторая итерация

n -ая

итерация

G 1

Y 0

Y 1

N

i

— число ненулевых элементов

Рис. 1. Итерационная процедура синтеза приспособленного ортогонального преобразования оператора

ПРИМЕНЕНИЕ ПРИСПОСОБЛЕННОГО ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ ДЛЯ ОЦЕНКИ ПАРАМЕТРОВ "НАЛОЖИВШИХСЯ" МАСС-СПЕКТРОМЕТРИЧЕСКИХ ПИКОВ РАЗЛИЧНОЙ ФОРМЫ

Масс-спектрометрические пики гауссовой формы

Рассмотрим масс-спектрометрический сигнал, представляющий собой смесь двух пиков одинаковой ширины, но различной амплитуды и разным положением на оси массовых чисел. Математически такой сигнал описывается выражением:

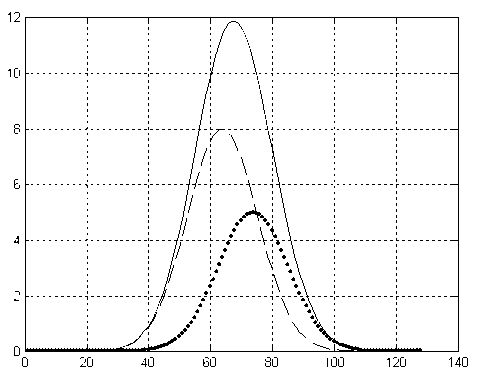
Рис. 2. "Наложившиеся" пики гауссовой формы. Сплошная линия — суммарный сигнал; пунктирная линия — сигнал F ₁; линия из точек — F ₂

S = F_x + F 2 ,

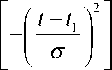
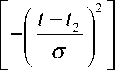
Сигнал S и его составляющие F ₁ и F ₂ представлены в виде графиков на рис. 2.

Алгоритм восстановления "наложившихся" пиков гауссовой формы представляется в виде последовательности следующих операций.

• 1)    Находим матрицу ортогонального преобразования в приспособленном базисе H в соответствии с формулой (1) для одиночного пика с помощью алгоритма, описанного выше.

• 2)    Находим вектор преобразованного сигнала в приспособленном базисе для одиночного пика F ₁ в соответствии с формулой

Y = HF,T .(6)

• 3)    Находим вектор преобразованного сигнала в приспособленном базисе для суммарного сигнала F + F 2 в соответствии с формулой

Y= H(F + F2)t.(7)

• 4)    Находим разность преобразованных сигналов

Y2 = Y - Y .(8)

• 5)    Выполняем обратное преобразование

yi = (HT Yi)/N,(9)

N — количество отсчетов в сигнале. Деление на количество отсчетов необходимо для согласования энергий сигнала в соответствии с равенством Парсе-валя.

На рис. 3 представлен сигнал после ортогонального преобразования в приспособленном базисе в соответствии с формулой (6).

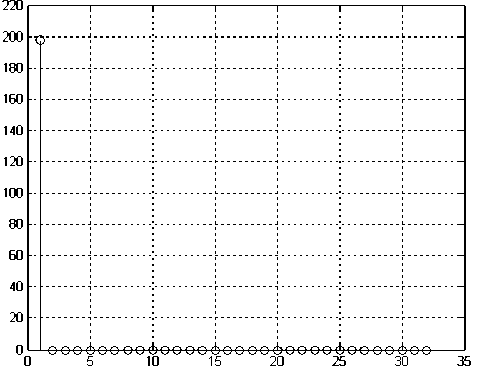
Рис. 3. Сигнал одиночного пика гауссовой формы после спектрального преобразования в приспособленном базисе для N = 32

На рис. 4 — сигнал после спектрального преобразования в приспособленном базисе для суммы F + F 2 ; на рис. 5 — сигнал после обратного спектрального преобразования в приспособленном базисе для разности сигналов Y 2 = Y 1 - Y .

Как показала проверка программы, реализующей описанный выше алгоритм, качество восстановления не зависит от количества отсчетов в сигнале. Проверка проводилась для N = 16, 32, 64, 128 и 256 и для эталонных сигналов, имеющих разную амплитуду и положение на оси независимой переменной.

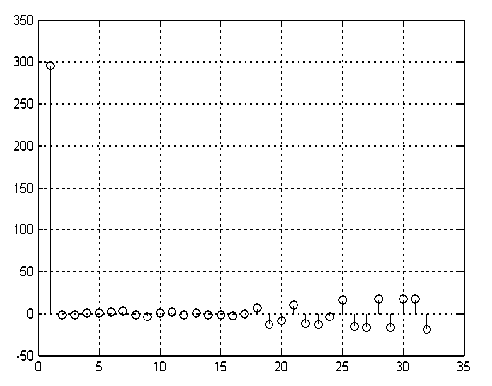
Рис. 4. Сигнал суммы F 1 + F 2 пиков гауссовой формы после спектрального преобразования в приспособленном базисе для N = 32

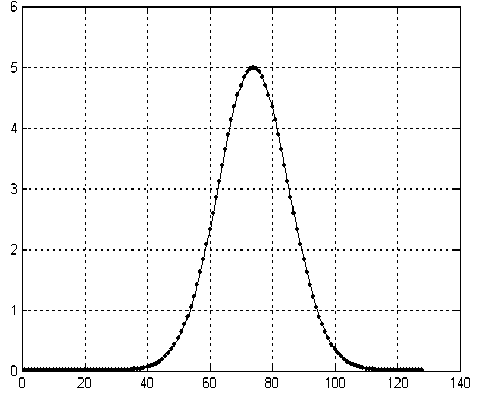
Рис. 5. Сигнал после обратного спектрального преобразования в приспособленном базисе для разности сигналов Y 2 = Y 1 - Y .

Сплошная линия — исходный сигнал F ₂ ; линия из точек — восстановленный сигнал

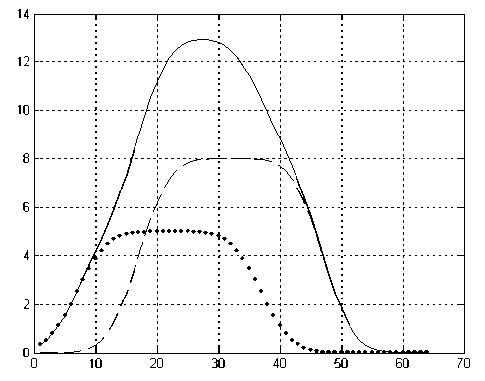
Рис. 6. "Наложившиеся" пики для масс-спектрометров с широкой щелью.

Сплошная линия — суммарный сигнал, пунктирная линия — сигнал F ₁, линия из точек — F ₂

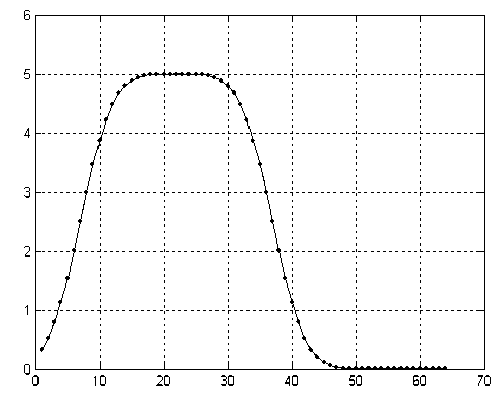
Рис. 7. Сигнал после обратного спектрального преобразования в приспособленном базисе для сигналов масс-спектрометров с широкой щелью. Сплошная линия — исходный сигнал F ₂ ; линия из точек — восстановленный сигнал

Масс-спектрометрические пики, отличные от гауссовой формы

Пусть

F = A

t2 -t ^ о V2 ,

I t — t+ Ф|  А

I о V2

где Φ — функция Лапласа. Такая форма пика получается в результате операции свертки пика гауссовой формы и прямоугольной функции, представляющей собой модель выходной щели масс-спектрометра; 1 2 - 1₁ — ширина щели.

В качестве F ₂ используем (9), но со смещением по оси независимой переменной на величину centr :

F 2 = A

( Л -1 - centr Ф1 -----=---

o V2

+ Ф

t -11 - centr V o V2    J

Суммарный сигнал — S = F + F ₂. Сигнал S и его составляющие F ₁ и F ₂ представлены в виде графиков на рис. 6. Аналогично сигналам гауссовой формы выполняем преобразования по алгоритму, описанному выше. В качестве эталонного сигнала для нахождения матрицы преобразования H используем сигнал, описанный формулой (9). Так же как и для сигналов гауссовой формы, ортогональное преобразование сигнала (9) в приспособленном базисе дает одну линию, аналогичную представленной на рис. 3.

Выполнив прямое преобразование сигнала S с помощью матрицы H , а затем обратное преобразование для разности преобразованных сигналов, получаем восстановленный сигнал F 2 . На рис. 7 представлены исходный и восстановленный сигналы.

Рассмотрим теперь сигналы, описываемые формулой (9), но искаженные динамическими свойствам регистрации. Как показано в работах [18–20], такие сигналы описываются в следующем виде:

F = conv[exp( - a t )sin m t , s m _O d ], (11)

где s _mod — сигнал, описываемый формулой (9), а conv — операция свертки сигналов в квадратных скобках, разделенных запятой. Параметр а характеризует инерционное звено системы регистрации, а m — колебательное звено. Характерной особенностью данных сигналов является относительно быстрый подъем на пик и медленный спад, что говорит о значительной постоянной времени регистрирующей системы. Сигнал F ₂ — аналогичный сигналу F ₁ , но смещенный на величину centr так же, как в формуле (10). Суммарный сигнал: S = F + F 2 . Сигнал S и его составляющие F и F 2 представлены в виде графиков на рис. 8. Восстановление сигналов данной формой производим по рассмотренному выше алгоритму. На рис. 9 представлены исходный и восстановленный сигналы.

ПРИМЕНЕНИЕ ПРИСПОСОБЛЕННОГО ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ ДЛЯ ФИЛЬТРАЦИИ МАСС-СПЕКТРОМЕТРИЧЕСКИХ СИГНАЛОВ

Рассмотрим возможности применения ортогонального преобразования в приспособленном базисе для фильтрации масс-спектрометрических сигналов на примере сигналов гауссовой формы.

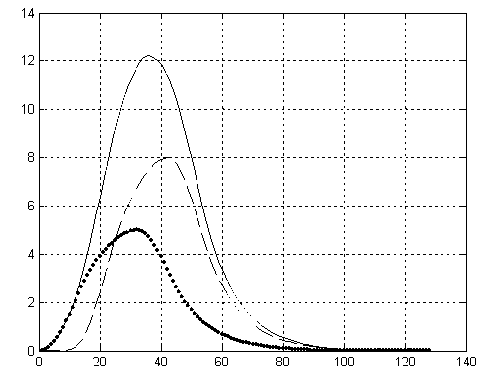
Рис. 8. "Наложившиеся" пики для сигналов масс-спектрометров с широкой щелью, искаженных динамическими свойствами регистрирующей системы.

Сплошная линия — суммарный сигнал; пунктирная линия — сигнал F ₁; линия из точек — F ₂

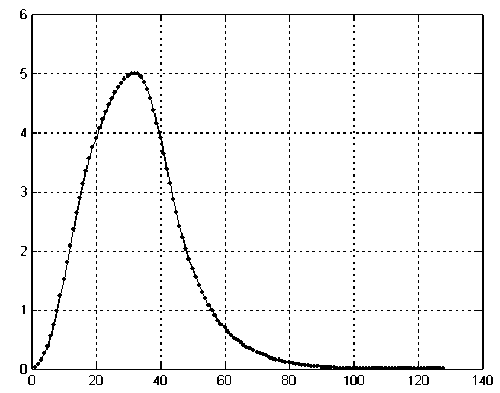
Рис. 9. Сигнал после обратного спектрального преобразования в приспособленном базисе для сигналов масс-спектрометров с широкой щелью, искаженных динамическими свойствами регистрирующей системы.

Сплошная линия — исходный сигнал F ₂ ; линия из точек — восстановленный сигнал

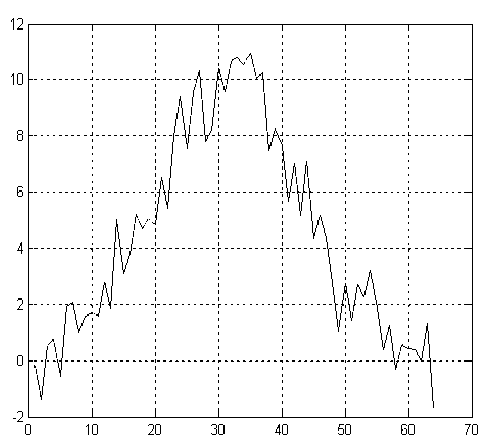
Рис. 10. Сигнал после добавления к пику гауссовой формы амплитудой 10 шума с нулевым средним и средним квадратичным отклонением, равным 1

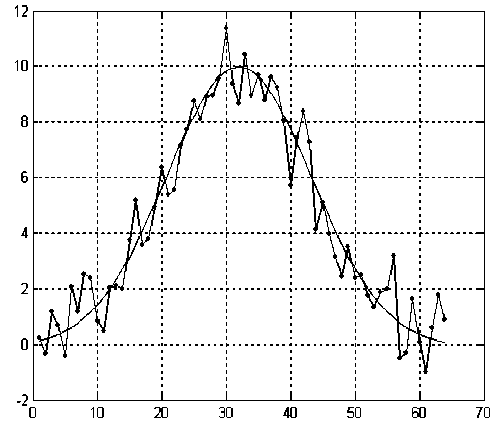
Рис. 11. Сигнал после фильтрации с помощью обратного спектрального преобразования в приспособленном базисе для гауссова сигнала.

Сплошная линия — восстановленный сигнал; линия из точек — исходный сигнал

Пусть F 3 = F + Ns, где F — сигнал гауссовой формы, описываемый формулой (5); Ns— шум с нормальной плотностью распределения и нулевым средним значением. На рис. 10 представлен график сигнала F ₁ с A ₁ =10 и средним квадратичным отклонением шума, равным 1.

Алгоритм фильтрации имеет следующую последовательность операций.

• 1.    Находим матрицу приспособленного преобразования H для сигнала известной формы F ₁ и амплитудой, равной 1.

• 2.    Находим вектор преобразованного сигнала в приспособленном базисе для одиночного пика F ₁ в соответствии с формулой (6).

• 3.    Применяем полученную матрицу преобразования для исходного сигнала F ₃ , но нормированного по среднему значению на вершине F _{3 N} :

T

• Y 1    ^HF 3 N •

• .4 . Находим разность преобразованных сигналов в соответствии с формулой (8).

• 5.    Выполняем обратное преобразование в соответствии с формулой (9).

• 6.    Производим вычитание из полученного сигнала y ₁ его среднего значения, умноженного на нормирующий коэффициент, вычисляемый при получении сигнала F _{3 N} (см. п. 3), и находим шумовой сигнал Ns1 .

• 7.    Вычитаем полученный шумовой сигнал Ns1

из исходного сигнала F ₃ .

Получается хорошо сглаженный сигнал, но его амплитуда отличается от исходного. Ошибки отличия тем меньше, чем больше отношение сигнала к шуму. Точность оценки амплитуды и качество сглаживания не зависят от количества точек в исходном сигнале.

На рис. 11 представлены исходный сигнал и сигнал после фильтрации с использованием ортогонального преобразования в приспособленном базисе.

ВЫВОДЫ

Рассмотренные алгоритмы разделения "наложившихся" пиков на основе ортогональных преобразований в приспособленном базисе имеют следующие основные преимущества:

• 1)    независимость от формы исходного сигнала;

• 2)    простота реализации;

• 3)    точность восстановления параметров пиков при использовании в качестве эталонного сигнала одиночного пика с известными параметрами.

В практических применениях некоторые параметры одиночного пика могут быть неизвестны, и поэтому в качестве эталонного сигнала пика целесообразно использовать пик известной формы и нормированной амплитуды. В этом случае рассмотренные алгоритмы могут быть использованы для решения следующих задач:

• 1)    нахождения начального приближения параметров "наложившихся" пиков для их отыскания методом наименьших квадратов;

• 2)    принятия решения о том, что в оцениваемом сигнале содержится несколько пиков (см. рис. 3 и 4).

Фильтрация сигналов с использованием преобразования в приспособленном базисе дает хорошо сглаженный сигнал, но точность восстановления параметров пиков зависит от отношения сигнала к шуму в исходном сигнале.